2023新生个人训练赛第08场解题报告

问题 A: Candies

题目描述

We have a 2×N grid. We will denote the square at the i-th row and j-th column (1≤i≤2, 1≤j≤N) as (i,j).
You are initially in the top-left square, (1,1). You will travel to the bottom-right square, (2,N), by repeatedly moving right or down.
The square (i,j) contains Ai,j candies. You will collect all the candies you visit during the travel. The top-left and bottom-right squares also contain candies, and you will also collect them.

At most how many candies can you collect when you choose the best way to travel?

Constraints
1≤N≤100
1≤Ai,j≤100 (1≤i≤2, 1≤j≤N)

输入

Input is given from Standard Input in the following format:
N
A1,1 A1,2 … A1,N
A2,1 A2,2 … A2,N

输出

Print the maximum number of candies that can be collected.

样例输入

5
3 2 2 4 1
1 2 2 2 1

样例输出

提示

The number of collected candies will be maximized when you:
move right three times, then move down once, then move right once.

AC Code:

#include <iostream>
#include <queue>
#include <cmath>
#include <algorithm>
#include <cstring>
#include <map>
#include <vector>
using namespace std;
const int maxn=1e2+10; 
int n;
int a[maxn][maxn];
int dp[maxn][maxn];
//dp   dp[i][j]=max(dp[i-1][j],dp[i][j-1])+a[i][j]
int max(int a,int b)
{
	return a>b?a:b;
}
void solve()
{
	dp[1][1]=a[1][1];
	for(int i=1;i<=2;i++)
	{
		for(int j=1;j<=n;j++)
		{
			if(i==1)
				dp[i][j]=dp[i][j-1]+a[i][j];
			else
				dp[i][j]=max(dp[i-1][j],dp[i][j-1])+a[i][j]; 
		}
	}
} 
int main()
{
	while(~scanf("%d",&n))
	{
	
	memset(a,0,sizeof(a));
	memset(dp,0,sizeof(dp));
	for(int i=1;i<=2;i++)
	{
		for(int j=1;j<=n;j++)
		{
			scanf("%d",&a[i][j]);
		}
	}
	solve();
	printf("%d\n",dp[2][n]);
}
	return 0;
}

问题 B: 传话游戏

题目描述

有这样一个朋友网络，如果a认识b，那么a收到某个消息，就会把这个消息传给b，以及所有a认识的人。但是，请你注意，如果a认识b，b不一定认识a。现在我们把所有人从1到n编号，给出所有“认识”关系，问如果i发布一条新消息,那么会不会经过若干次传话后，这个消息传回给了i（1≤i≤n）。

输入

第1行是两个数n（n<1000）和m（m<10000），两数之间有一个空格，表示人数和认识关系数。接下来的m行，每行两个数a和b，表示a认识b（1≤a,b≤n）。认识关系可能会重复给出，但1行的两个数不会相同。

输出

一共有n行，每行一个字符T或F。第i行如果是T，表示i发出一条新消息会传回给i；如果是F，表示i发出一条新消息不会传回给i。

样例输入

样例输出

T
T
T
F

AC Code:

#include <iostream>
#include <queue>
#include <cmath>
#include <algorithm>
#include <cstring>
#include <map>
#include <vector>
int i[1001][10001];
int n,m,T;
bool Vis[1001],f[1001];
void DFS(int t)
{
    if (f[T]) //找到了就返回。
      return;
    Vis[t]=true;
    if (t==T) //重合即为环。
    {
        f[T]=true;
        return;
    }
    for (int a=1;a<=i[t][0];a++)
      if (!Vis[i[t][a]]) //未找过。
        DFS(i[t][a]);
}
int main() //普通DFS。
{
    scanf("%d%d",&n,&m);
    for (int a=1;a<=m;a++)
    {
        int t1,t2;
        scanf("%d%d",&t1,&t2);
        i[t1][0]++; //节省空间，邻接点数量。
        i[t1][i[t1][0]]=t2;
    }
    for (T=1;T<=n;T++)
    {
        memset(Vis,false,sizeof(Vis));
        for (int a=1;a<=i[T][0];a++)
          DFS(i[T][a]); //DFS每条边。
    }
    for (int a=1;a<=n;a++)
      if (f[a])
        printf("T\n");
      else
        printf("F\n");
    return 0;
}

问题 C: 冬眠

题目描述

麻雀帕西和青蛙弗洛格是好玩伴，它们经常一起比赛唱歌。但冬天来了，青蛙弗洛格冬眠了，它的睡眠深度是D。麻雀帕西觉得好无聊，于是它想办法要唤醒弗洛格。麻雀帕西只会唱N首歌，第i首歌的音量是Si。每听完一首歌，青蛙弗洛格的睡眠深度就会减少，减少的值等于它听到的歌的音量。当青蛙弗洛格的睡眠深度大于0的时候，它会继续冬眠，当睡眠深度小于或者等于0时，它就会被唤醒了。麻雀帕西会从第1首歌开始唱，唱完第1首歌后如果弗洛格还没醒就接着唱第2首歌，如果唱完第2首歌弗洛格还没醒就接着唱第3首歌，依次类推，如果唱完第N首歌后弗洛格还没醒，那么麻雀帕西又重新从第1首歌开始唱，就像循环播放音乐一样，一直到青蛙弗洛格被唤醒为止，那么麻雀帕西总共唱了多少首歌？

输入

第一行，两个整数： D 和 N。
第二行，N个整数，空格分开，第i个整数就是第i首歌的音量Si。

输出

一个整数，麻雀帕西总共唱了多少首歌后，弗洛格会被唤醒？

样例输入

13  3
5  2  4

样例输出

提示

麻雀帕西唱完第1首歌后，青蛙弗洛格睡眠深度变成8，
麻雀帕西唱完第2首歌后，青蛙弗洛格睡眠深度变成6，
麻雀帕西唱完第3首歌后，青蛙弗洛格睡眠深度变成2，
麻雀帕西再次唱完第1首歌后，青蛙弗洛格睡眠深度变成-3，青蛙弗洛格会被唤醒。

对80%的数据，1 ≤ D ≤ 10000，1 ≤ N ≤ 50，1 ≤ Si ≤ 100。
另外20%的数据，1 ≤ D ≤ 2000000000，1 ≤ N ≤ 50，1 ≤ Si ≤ 3。

AC Code:

#include <iostream>
#include <queue>
#include <cmath>
#include <algorithm>
#include <cstring>
#include <map>
#include <vector>
using namespace std;
typedef long long ll;
ll a[51], n, d, i = 0, s = 0;
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    cin >> d >> n;
    for (int j = 0; j < n; j++)
    {
        cin >> a[j];
        s += a[j];
    }
    while (d > s)
    {
        d -= s;
        i += n;
    }
    while (d > 0)
    {
        d -= a[i % n];
        i++;
    }
    cout << i;
    return 0;
}

问题 E: 查找特定的合数

题目描述

自然数中除了能被1和本身整除外，还能被其他数整除的数叫合数。每个合数都可以写成几个质数相乘的形式，这几个质数都叫做这个合数的质因数。比如8=2×2×2，2就是8的质因数。在1—N（N≤200000）按从小到大顺序排列的自然数序列中，查找第M个有X（2≤X≤6）个不同质因数的合数。例如，第3个有2个不同质因数的合数是12（12只有2、3两个不同的质因数，在12之前有2个不同质因数的合数分别为6和10）。

输入

共1行，分别为M，X。

输出

共1行，为第M个有X个不同质因数的合数。

样例输入

3 2

样例输出

AC Code:

#include <iostream>
#include <queue>
#include <cmath>
#include <algorithm>
#include <cstring>
#include <map>
#include <vector>
typedef long long LL;
using namespace std;
int m, x;
int tot, vis[200005], prim[200005];
void init(){   //筛素数
	for (int i = 2; i <= 200000; i++){
		if(!vis[i]) prim[tot++] = i;
		for (int j = 0; j < tot && prim[j] * i <= 200000; j++){
			vis[i * prim[j]] = 1;
			if(i % prim[j] == 0) break;
		}
	}
}
int main()
{
	init();
	scanf("%d %d", &m, &x);
	int ans = 0;
	for (int i = 4; i <= 200000; i++){
		if(!vis[i]) continue;
		int num = 0;
		int t = sqrt((double) i);
		for (int j = 2; j <= t; j++){
			if(i % j == 0){
				if(!vis[j]) num++;
				if(!vis[i / j] && j * j != i) num++;
			}
			if(num > x) break;
		}
		if(num == x) ans++;
		if(ans == m){
			printf("%d\n", i);
			break;
		}
	}
	return 0;
}

问题 F: People on a Line

题目描述

There are N people standing on the x-axis. Let the coordinate of Person i be xi. For every i, xi is an integer between 0 and 109 (inclusive). It is possible that more than one person is standing at the same coordinate.
You will given M pieces of information regarding the positions of these people. The i-th piece of information has the form (Li,Ri,Di). This means that Person Ri is to the right of Person Li by Di units of distance, that is, xRi−xLi=Di holds.
It turns out that some of these M pieces of information may be incorrect. Determine if there exists a set of values (x1,x2,…,xN) that is consistent with the given pieces of information.

Constraints
1≤N≤100 000
0≤M≤200 000
1≤Li,Ri≤N (1≤i≤M)
0≤Di≤10 000 (1≤i≤M)
Li≠Ri (1≤i≤M)
If i≠j, then (Li,Ri)≠(Lj,Rj) and (Li,Ri)≠(Rj,Lj).
Di are integers.

输入

Input is given from Standard Input in the following format:
N M
L1 R1 D1
L2 R2 D2
:
LM RM DM

输出

If there exists a set of values (x1,x2,…,xN) that is consistent with all given pieces of information, print Yes; if it does not exist, print No.

样例输入

样例输出

Yes

提示

Some possible sets of values (x1,x2,x3) are (0,1,2) and (101,102,103).

AC Code:

#include <iostream>
#include <string>
#include <cstdio>
#include <cmath>
#include<cstring>
#define max(x,y) x>y?x:y
using namespace std;
const int maxn=1011111;
int f[maxn];
int d[maxn];
int find(int x)
{
    if(f[x]==x)
        return x;
 
    int r=find(f[x]);
    d[x]=d[f[x]]+d[x];//当前x到她老祖宗的距离等于他现在的距离加上她爸爸到老祖宗的距离
 
    return f[x]=r; //把每个子节点合并到他的祖先
}
 
 
int fix(int x,int y,int z)
{
    int fx=find(x);
    int fy=find(y);
    if(fx==fy)
        return z==d[y]-d[x];
    f[fy]=fx;//把x当作y的爸爸；
    d[fy]=d[x]+z-d[y];
    return 1;
}
int main()
{
    int n,m;
    int lose=1;
    cin>>n>>m;
    for(int i=1;i<=n;i++)//初始化
        f[i]=i;
    for(int i=1;i<=m;i++)
    {
        int x,y,z;
        cin>>x>>y>>z;
 
        if(lose)
            lose=fix(x,y,z);
 
    }
 
    if(lose)
        cout<<"Yes";
    else
        cout<<"No";
    return 0;
}

问题 G: 电子警察

题目描述

现在很多地方的道路路口都安装了电子警察，即交通违章自动拍照系统。这些系统一般在路口的地下埋设感应线圈，通过传感器判断汽车是否在红灯时通过路面，来控制数码相机自动拍照。在安装这种系统需要挖掘地面，施工麻烦，成本又高。于是有人研究出了同摄像机自动识别车牌并判断违章行为的系统，这样一来，电子警察安装就方便多了，成本也大大降低。请你编程实现其中的一个功能，给出一批某一时间识别后的车牌号码及行进方向，判断该车是否违章，并记录下来。违章的规则设定为：先设置左转、直行、右转依次绿灯通行时间（以秒为单位，只允许一个方向绿灯），先左转绿灯，然后直行绿灯，最后右转绿灯，在其中一个绿灯时，其余两盏灯为红灯状态，假设时间生效在零时整，且给出的数据只限定当天。闯红灯为违章。

输入

第1行有4个整数，以一个空格隔开，依次为左转、直行、右转通行的绿灯持续秒数和识别的车辆数N（1≤N≤10000），后面的N行，表示每辆车的信息，格式为“时间+方向+车牌”，其中时间为6位数字，方向为1个字母（L表示左转，S表示直行，R表示右转），车牌为8个字符，之间没有空格。如081528LZJBB0001，表示车牌号为ZJBB0001的车辆在8时15分28秒左转。

输出

违章车辆的车牌号码，每辆车一行，不含空格，按输进去的先后顺序输出。

样例输入

15 30 20 3
000046SZJBB8888
030950LJSAA9999
201509RBJC7777D

样例输出

ZJBB8888
BJC7777D

AC Code:

#include <iostream>
#include <queue>
#include <cmath>
#include <algorithm>
#include <cstring>
#include <map>
#include <vector>
using namespace std;
int main()
{
    char a[20];
    int n, i, l, s, r, c, j, d;
    scanf("%d %d %d %d", &l, &s, &r, &n);
    while (getchar() != '\n')
        ;      // 处理行末空格，不加while会WA
    s = l + s; // s此时代表直行结束的时刻
    r = s + r; // r此时代表右转结束的时刻，即一个周期的时长
    while (n-- > 0)
    {
        cin.getline(a,N);
        c = 0; // c代表从计时开始共经历的时间长度对总时长取余后的结果
        for (j = 0; j < 3; j++)
        {
            d = 0;
            for (i = j * 2; i < j * 2 + 2; i++)
                d = d * 10 + a[i] - '0';
            c = c * 60 + d;
            c = c % r;
        }
        if ((a[6] == 'L' && (c == 0 || c > l)) || (a[6] == 'S' && (c <= l || c > s)) || (a[6] == 'R' && c <= s && c != 0))
            puts(a + 7);
    }
    return 0;
}

问题 H: 小矮人

题目描述

最初出现“七个小矮人”的是德国著名童话集《格林童话》之中的《白雪公主》。原文讲述了一个可爱美丽的公主因为被恶毒后母嫉妒其美貌而被迫逃到森林，在缘分安排下偶遇善良的七个小矮人。最后在他们帮助下，破解了后母的诅咒，找到了王子的真爱的故事。七个小矮人的姓名分别是：万事通、害羞鬼、瞌睡虫、喷嚏精、开心果、迷糊鬼、爱生气。白雪公主经常为这七个小矮人讲故事。白雪公主还为这七个小矮人安排了学号，学号分别是1至7号。有一次，白雪公主又邀请七个小矮人来听她讲故事，但是只来了六个小矮人，那么缺席的那个小矮人是谁呢？

输入

一行，6个学号，空格分开，表示来听故事的六个小矮人的学号。

输出

没来听故事的小矮人的学号。

样例输入

3 5 2 1 7 4

样例输出

6

AC Code:

#include <iostream>
#include <queue>
#include <cmath>
#include <algorithm>
#include <cstring>
#include <map>
#include <vector>
using namespace std;
map<int, int> mp;
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    for (int i = 1; i <= 7; i++)
    {
        mp[i] = 1;
    }
    int x;
    for (int i = 0; i < 6; i++)
    {
        cin >> x;
        mp[x]++;
    }
    map<int, int>::iterator it;
    for (it = mp.begin(); it != mp.end(); it++)
    {
        if (it->second == 1)
        {
            cout << it->first;
            return 0;
        }
    }
    return 0;
}

问题 I: Avoiding Collision

题目描述

We have a graph with N vertices and M edges, and there are two people on the graph: Takahashi and Aoki.
The i-th edge connects Vertex Ui and Vertex Vi. The time it takes to traverse this edge is Di minutes, regardless of direction and who traverses the edge (Takahashi or Aoki).
Takahashi departs Vertex S and Aoki departs Vertex T at the same time. Takahashi travels to Vertex T and Aoki travels to Vertex S, both in the shortest time possible. Find the number of the pairs of ways for Takahashi and Aoki to choose their shortest paths such that they never meet (at a vertex or on an edge) during the travel, modulo 109+7.

Constraints
1≤N≤100 000
1≤M≤200 000
1≤S,T≤N
S≠T
1≤Ui,Vi≤N (1≤i≤M)
1≤Di≤109 (1≤i≤M)
If i≠j, then (Ui,Vi)≠(Uj,Vj) and (Ui,Vi)≠(Vj,Uj).
Ui≠Vi (1≤i≤M)
Di are integers.
The given graph is connected.

输入

Input is given from Standard Input in the following format:
N M
S T
U1 V1 D1
U2 V2 D2
:
UM VM DM

输出

Print the answer.

样例输入

4 4

1 3

1 2 1

2 3 1

3 4 1

4 1 1

样例输出

2

提示

There are two ways to choose shortest paths that satisfies the condition:
Takahashi chooses the path 1→2→3, and Aoki chooses the path 3→4→1.
Takahashi chooses the path 1→4→3, and Aoki chooses the path 3→2→1.

AC Code:

#include <iostream>
#include <queue>
#include <cmath>
#include <algorithm>
#include <cstring>
#include <map>
#include <vector>
#define MAXN 100005
#define INF 0x3f3f3f3f
#define pb push_back
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<ll,int>P;
vector<P>G[MAXN];
const int mod=1e9+7;
struct Edge
{
    int u,v,w;
}edge[MAXN*2];

ll dis[2][MAXN],cnt[2][MAXN];
int vis[MAXN];
void dijkstra(int id,int s)
{
    memset(dis[id],60,sizeof(dis[id]));
    memset(vis,0,sizeof(vis));
    dis[id][s]=0;
    cnt[id][s]=1;
    priority_queue<P,vector<P>,greater<P> >q;
    q.push(P(0,s));
    while(!q.empty())
    {
        P p=q.top();q.pop();
        int x=p.second;
        if(vis[x])continue;
        vis[x]=1;
        for(P e:G[x])
        {
            int to=e.second;//cout<<x<<' '<<to<<' '<<dis[id][to]<<endl;
            ll w=e.first;
            if(dis[id][to]>dis[id][x]+w)
            {
                dis[id][to]=dis[id][x]+w;
                cnt[id][to]=cnt[id][x];
                q.push(P(dis[id][to],to));
            }
            else if(dis[id][to]==dis[id][x]+w)
                cnt[id][to]=(cnt[id][to]+cnt[id][x])%mod;
        }
    }
}

int main(){
    int n,m;scanf("%d%d",&n,&m);
    int s,t;scanf("%d%d",&s,&t);
    for(int i=1;i<=m;i++)
    {
        int u,v,w;scanf("%d%d%d",&u,&v,&w);
        edge[i]={u,v,w};
        G[u].pb(P(w,v));
        G[v].pb(P(w,u));
    }
    dijkstra(0,s);
    dijkstra(1,t);
    ll ans=cnt[0][t]*(cnt[0][t]-1)%mod;//cout<<ans<<endl;
    for(int i=1;i<=n;i++)
    {
        if(dis[0][i]==dis[1][i]&&dis[0][i]*2==dis[0][t])
        {
            ll tmp=cnt[0][i]*cnt[1][i]%mod;
            ans=(ans-tmp*(tmp-1)%mod+mod)%mod;
        }
    }
    for(int i=1;i<=m;i++)
    {
        int u=edge[i].u,v=edge[i].v,w=edge[i].w;
        if(dis[0][u]>dis[0][v])swap(u,v);
        if(dis[0][u]+dis[1][v]+w==dis[0][t]&&dis[0][u]*2<dis[0][t]&&dis[1][v]*2<dis[0][t])
        {
            ll tmp=cnt[0][u]*cnt[1][v]%mod;
            ans=(ans-tmp*(tmp-1)%mod+mod)%mod;
        }
    }
    printf("%lld\n",ans);
    return 0;
}

问题 J: Buying Sweets

题目描述

You went shopping to buy cakes and donuts with X yen (the currency of Japan).
First, you bought one cake for A yen at a cake shop. Then, you bought as many donuts as possible for B yen each, at a donut shop.
How much do you have left after shopping?

Constraints
1≤A,B≤1 000
A+B≤X≤10 000
X, A and B are integers.

输入

Input is given from Standard Input in the following format:
X
A
B

输出

Print the amount you have left after shopping.

样例输入

1234

150

100

样例输出

84

提示

You have 1234−150=1084 yen left after buying a cake. With this amount, you can buy 10 donuts, after which you have 84 yen left.

AC Code:

//C++入门题
#include <iostream>
#include <queue>
#include <cmath>
#include <algorithm>
#include <cstring>
#include <map>
#include <vector>
using namespace std;
typedef long long ll;
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    int x, a, b;
    cin >> x >> a >> b;
    x -= a;
    cout << x - (x / b) * b;
    return 0;
}

问题 K: 弗洛格

题目描述

青蛙弗洛格和它的妈妈是火星动物，在火星上，每年都有12个月，每个月的天数都是30天，每个月都是从1号开始，然后是2号，...，每月的最后一天都是30号。弗洛格妈妈想考查一下弗洛格的数学水平，于是问道：“今天是几号？”，弗洛格回答：“27号！”，妈妈说：“正确！”。妈妈接着问：“前1天是几号？”，弗洛格回答：“26号！太简单了！我读一年级就会了！”。妈妈再问：“前N天是几号？”，弗洛格皱起眉头：“这个有点难，我要写个程序来算”。由于弗洛格的编程水平一般，你能帮帮它吗?

输入

一个整数N，表示妈妈问弗洛格，前N天是几号？

输出

一个整数。

样例输入

2

样例输出

25

提示

对于90%的数据，1 ≤ N ≤ 26。即问题的答案一定是本月的某一天。
另外10%的数据，27 ≤ N ≤ 50。

AC Code:

//数据范围小,分类讨论即可

#include <iostream>
#include <queue>
#include <cmath>
#include <algorithm>
#include <cstring>
#include <map>
#include <vector>
using namespace std;
int father, mother, me;
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    int n;
    cin >> n;
    if (n >= 1 && n <= 26)
        cout << (27 - n);
    else if (n >= 27 && n <= 50)
    {
        cout << (30 - (n - 26) + 1);
    }
    return 0;
}

问题 L: 机器人的逻辑

题目描述

2035年，智能机器人在各行各业中的应用已经十分普遍了，毕竟它做事时的精度与力量比一个普通人是强多了。
王涛的运输队里就有一个，是用来装卸货物的。
这天，他们的任务是要把n根废旧的条形钢材运送到钢铁厂重新冶炼。这些钢材长短不同（有些还特别的长），为了便于运输，只好把它们切割成小段。所以，他给机器人的任务是：把这些钢材切割并装上卡车。
等机器人做完这事的时候，王涛一看结果，自己都被逗笑了：机器人的逻辑就是和人不同啊——装在车上的所有小段的钢材，居然长度都是一样的（以米为单位），而且，还是所有可行方案中，切割次数最少的那种方案！
如果告诉你最开始那n根钢材的长度，你能算出机器人切割出的小段的长度吗？

输入

第一行为整数n，表示原始钢材的数量。
第二行中是n个用空格分开的整数，表示每根废旧钢材的长度（以米为单位），已知这些整数不小于1，不超过400000。

输出

只有一个整数，表示机器人切割出来的每个小段的长度。

样例输入

4

4

22

8

12

样例输出

2

AC Code:

//求这n个数的最大公约数
#include <iostream>
#include <queue>
#include <cmath>
#include <algorithm>
#include <cstring>
#include <map>
#include <vector>
using namespace std;
typedef long long ll;
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    int n, x;
    cin >> n;
    int gcd = 0;
    while (n--)
    {
        cin >> x;
        gcd = __gcd(gcd, x);
    }
    cout << gcd;
    return 0;
}

问题 M: 围墙重建

题目描述

为了给同学们营造一个良好的学习环境和方便学校的管理，市政府准备对小W就读的学校进行重新规划,占地面积将再次扩大。学校通过领导会议决定，重建学校的围墙。由于学校太大，重建围墙也不是一件小项目，学校决定请专门的建筑公司来建筑。
许多建筑公司从网上得知这个消息后，纷纷来到学校，找到学校领导，对自己公司进行介绍，并希望能接下这个项目。学校领导对很多家公司印象都还不错，难以取舍，为了公平，学校决定通过竞标决定把这个项目交给哪家公司负责。这次竞标是由学校自主决定的，不但要注重建筑实力，而且还要看建筑公司是否有足够的智慧。
学校通过两轮选拔。第一轮，选出建筑实力较强的公司。进入第二轮后，由学校专门负责这个项目的领导进行智力考核。
领导说：为了美观，我们准备建设一面2米高的围墙，围墙建好后，墙外要贴上有图画的瓷砖,当然这就需要瓷砖越大越美观了。目前市面用的最大瓷砖是多大？
公司：宽1米，长2米的
领导：哦，我们就用这种吧，我们学校现需建筑N米长的围墙，如果用这种瓷砖来贴，总共有多少种贴法呢？
公司：…………….（正在计算中……………）

输入

只有一个整数N（1<N<10000），表示围墙的长度。

输出

只有一个数，表示如果用宽1米、长2米的瓷砖，贴在高2米，长N米的围墙上，最多有多少种不同的贴法？

样例输入

4

样例输出

5

提示

对于20%的数据，2<N<90；
对于60%的数据，2<N ≤1200；
对于100%的数据，2< N<10000。

AC Code:

#include <iostream>
#include <queue>
#include <cmath>
#include <algorithm>
#include <cstring>
#include <map>
#include <vector>
using namespace std;
int a,b,c,c1,c2;
int n[100000],n1[100000],n2[100000];
void j(int a[],int b[],int d[]){
    int x=0;
    c2=c1;
    for(int i=1;i<=c2;i++)
    {
        d[i]=a[i]+b[i]+x;
        x=d[i]/10;
        d[i]%=10;
    }
    if(x!=0)
        c2++,d[c2]=x;
}
void f(int &ac,int &bc,int a[],int b[]){
    for(int i=1;i<=bc;i++)
        a[i]=b[i];
    ac=bc;
}
int main() {
    c = c1 = 1;
    n[1] = n1[1] = 1;
    cin >> a;
    for (int i = 2; i <= a; i++) {
        j(n, n1, n2);
        f(c, c1, n, n1);
        f(c1, c2, n1, n2);
    }
    for (int i = c1; i >= 1; i--)
        cout << n1[i];
    return 0;
}

问题 N: 小米

题目描述

小米同学现在读四年级，小米同学想知道自己成年后的身高大概是多少。于是小米同学上网查找资料，终于找到了一条计算公式：
1、如果小米是男生，那么成年后身高 = （父亲身高＋母亲身高＋13厘米）div 2
2、如果小米是女生，那么成年后身高 = （父亲身高＋母亲身高－13厘米） div 2

输入

一行，三个整数：father、mother、me。其中father是父亲身高，mother是母亲身高，me如果是1，则代表小米是男生；me如果是0，则代表小米是女生。（140 ≤ father ≤ 200，140 ≤ mother ≤ 200。 me=1或者me=0。）

输出

一个整数，表示小米同学成年后的身高。

样例输入

174 162 0

样例输出

161

提示

父亲身高174，母亲身高161，小米是女生，因此身高是
（174＋162－13）div 2 ＝　323 div 2 = 161

题目中的div是表示整除， A div B 表示的意义是A除以B的商，忽略余数。
例如： 10 div 2 = 5，因为10除以2的商是5。 9 div 2 = 4，因为9除以2的商是4。

AC Code:

#include <iostream>
#include <queue>
#include <cmath>
#include <algorithm>
#include <cstring>
#include <map>
#include <vector>
using namespace std;
int father, mother, me;
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    int ans = 0;
    cin >> father >> mother >> me;
    if (me == 0)
    {
        ans = (father + mother - 13) / 2;
    }
    else if (me == 1)
    {
        ans = (father + mother + 13) / 2;
    }
    cout << ans;
    return 0;
}

问题 O: 魔方

题目描述

魔方大家都玩过吧？
常见的魔方，每边上有3个小正方体，如下图所示：

我们把魔方每边上的小正方体数量，叫魔方的“阶”，所以，常见的魔方叫“3阶魔方”。不过，魔方可不是只有3阶的，还有2、4、5……阶的呢，如下图所示：

观察所有的魔方，你会发现，我们可以把魔方表面上的小正方体分为三类：
第一类：有三个面露在外面的；
第二类：有两个面露在外面的；
第三类：有一个面露在外面的。
当然，这三类小正方体的数量会随着魔方阶的不同而不同。你的任务就是计算一下，对于给定阶数的魔方，这三类小正方体分别有多少个?

输入

只有一个整数n，表示魔方的阶数，已知2≤n≤1000。

输出

有三行，每行一个整数，分别表示对于n阶的魔方，第一类、第二类、第三类的小正方体的数量。

样例输入

3

样例输出

8

12

6

AC Code:

#include <iostream>
#include <queue>
#include <cmath>
#include <algorithm>
#include <cstring>
#include <map>
#include <vector>
using namespace std;
typedef long long ll;
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    int a, a1, a2, a3;
    cin >> a;
    a1 = 8;
    a2 = (a - 2) * 12;
    a3 = (a - 2) * (a - 2) * 6;
    cout << a1 << endl<< a2 << endl << a3;
    return 0;
}

问题 P: Coins III

题目描述

You have A 500-yen coins, B 100-yen coins and C 50-yen coins (yen is the currency of Japan). In how many ways can we select some of these coins so that they are X yen in total?
Coins of the same kind cannot be distinguished. Two ways to select coins are distinguished when, for some kind of coin, the numbers of that coin are different.

Constraints
0≤A,B,C≤50
A+B+C≥1
50≤X≤20 000
A, B and C are integers.
X is a multiple of 50.

输入

Input is given from Standard Input in the following format:

A
B
C
X

输出

Print the number of ways to select coins.

样例输入

2

2

2

100

样例输出

2

提示

here are two ways to satisfy the condition:
Select zero 500-yen coins, one 100-yen coin and zero 50-yen coins.
Select zero 500-yen coins, zero 100-yen coins and two 50-yen coins.

AC Code:

//暴力枚举
#include <iostream>
#include <queue>
#include <cmath>
#include <algorithm>
#include <cstring>
#include <map>
#include <vector>
using namespace std;
int father, mother, me;
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    int x, a, b, c;
    cin >> a >> b >> c >> x;
    int sum = 0;
    for (int i = 0; i <= a; i++)
    {
        for (int j = 0; j <= b; j++)
        {
            for (int k = 0; k <= c; k++)
            {
                if ((i * 500 + j * 100 + k * 50) == x)
                    sum++;
            }
        }
    }
    cout << sum;
    return 0;
}

问题 Q: 录取分数线

题目描述

新学年，学校将成立信息学兴趣小组提高班。由于指导教师精力有限，只能以选拔考试的成绩为依据，按从高到低的分数，从N个参加选拔的学生中录取不超过M个成员。录取的成员要尽可能地多，但不得超过M个（含M个）。由于可能会有并列分数出现，为了保证公平，有时只得忍痛割爱，可能录取的成员会达不到计划数M。请你编程划定录取分数线。

输入

有N+1行，第一行是报名人数N和录取人数M。以下N行是考试成绩，已按从高到低的顺序排列。N、M和成绩均是1000以内的正整数，N≥M。数据保证不会所有的成绩都相同。

输出

只有1行，为录取分数线。

样例输入

10 5

99

98

97

96

95

94

93

92

91

90

样例输出

95

AC Code:

#include <iostream>
#include <queue>
#include <cmath>
#include <algorithm>
#include <cstring>
#include <vector>
using namespace std;
typedef long long ll;
const int N = 5e6 + 5;
int n, m, a[N];
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
        cin >> a[i];
    if(a[m]!=a[m+1])
        cout << a[m];
    else{
        for(int i=m;~i;i--)
        {
            if(a[i]>a[m])
            {
                cout << a[i];
                return 0;
            }
        }
    }
    return 0;
}

问题 R: 小球

题目描述

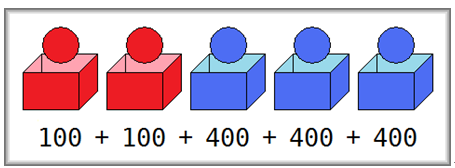
有R个红色盒子和B个蓝色盒子，还有R个红色小球和B个蓝色小球。每个盒子只能装一个小球，每个小球都要放在一个盒子里。如果把一个红色小球放在一个红色盒子里，那么得分是C。如果把一个蓝色小球放在一个蓝色盒子里，那么得分是D。如果把一个红色小球放在一个蓝色盒子里，那么得分是E。如果把一个蓝色小球放在一个红色盒子里，那么得分也是E。现在给出R，B，C，D，E。应该如何放置这些小球进盒子，才能使得总得分最大？输出最大的总得分。

输入

一行，5个整数，分别是R，B，C，D，E。（1 ≤ R ≤ 100，1 ≤ B ≤ 100， -1000 ≤ C，D，E ≤ 1000）

输出

一个整数，最大总得分。

样例输入

2 3 100 400 200

样例输出

1400

提示

AC Code:

#include <iostream>
#include <queue>
#include <cmath>
#include <algorithm>
#include <cstring>
#include <map>
#include <vector>
using namespace std;
typedef long long ll;
int r, b, c, d, e, sum;
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    bool k;
    cin >> r >> b >> c >> d >> e;
    if (r > b)
        k = 1;
    else
        k = 0;
    if (c + d > e + e)
        sum = r * c + b * d;
    else
    {
        if (k)
            sum = b * 2 * e + (r - b) * c;
        else
            sum = r * 2 * e + (b - r) * d;
    }
    cout << sum;
    return 0;
}

问题 S: 允许并列的排名

题目描述

在我们参加的各种竞赛中，允许并列的排名方式是经常遇到的。
例如有四名选手的成绩分别为50、80、50、30分，则80分的选手为第一名，50分的两名选手均为第二名，30分的选手为第四名。
请你编写一个程序，计算一个选手在这种排名方式之下的名次（分数高的选手排前面）。

输入

第一行为一个整数n，表示参赛的选手数，1≤n≤100；
第二行为n个整数，表示每位选手的成绩；
第三行为一个整数，表示要查询名次的选手的成绩。

输出

有一个整数，表示该选手的名次。

样例输入

4

50 80 50 30

50

样例输出

2

AC Code:

#include <iostream>
#include <queue>
#include <cmath>
#include <algorithm>
#include <cstring>
#include <map>
#include <vector>
using namespace std;
typedef long long ll;
int a[100];
int i, j, r, n;
int x = 0, y;
int m, t = 1, z, w = 1;
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    cin >> n;
    for (i = 0; i < n; i++)
    {
        cin >> y;
        a[x] = y;
        x++;
    }
    cin >> m;
    for (i = 0; i < n; i++)
    {
        if (a[i] > m)
            t++;
    }
    cout << t;
    return 0;
}

问题 T: 变形虫

题目描述

Bessie是一只变形虫，一开始它的体重是A。在地板上从左往右依次放着N块蛋糕，第i块蛋糕的重量是Wi。变形虫从左边爬到右边，每次遇到一块蛋糕，如果蛋糕的重量恰好等于变形虫当前的重量，那么变形虫就吃掉这块蛋糕，吃完蛋糕后变形虫的重量增加了一倍；如果蛋糕的重量不等于变形虫当前的重量，那么变形虫永远也吃不了这块蛋糕了。变形虫只能从左往右爬，不能吃了某蛋糕后再往左爬。你的任务是计算变形虫的最终体重是多少。

输入

第一行，两个整数：A，N。
第二行，N个整数，空格分开，第i个整数就是第i块蛋糕的重量Wi。（1 ≤ A ≤ 1000000000，1 ≤ N ≤ 200，1 ≤ Wi ≤ 1000000000。）

输出

一个整数，变形虫的最终体重。

样例输入

1 5

2 1 3 1 2

样例输出

4

提示

变形虫首先会吃掉第2块蛋糕，体重变成2。然后变形虫再吃掉第5块蛋糕，体重变成4。

AC Code:

#include <iostream>
#include <queue>
#include <cmath>
#include <algorithm>
#include <cstring>
#include <map>
#include <vector>
using namespace std;
typedef long long ll;
ll a[210], w;
int n;
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    cin >> w >> n;
    for (int i = 1; i <= n; i++)
    {
        cin >> a[i];
    }
    for (int i = 1; i <= n; i++)
    {
        if (a[i] == w)
            w <<= 1;
        else
            continue;
    }
    cout << w;
    return 0;
}