目录

前言

1.二叉树的链式存储

2.二叉链表的表示和实现

1.定义

2.创建

4.中序遍历二叉树

5.后序遍历二叉树

6.后序遍历二叉树

7.完整代码

---

前言

    这篇博客主要介绍二叉树的链式存储结构。

1.二叉树的链式存储

       上篇文章中介绍了二叉树的顺序存储结构，在最坏的情况下，比如二叉树仅有左子树或者右子树的时候，我们仍然需要为不存在的节点分配大量的存储空间，这无疑会造成存储空间的浪费。考虑到二叉树的三要素：数据域、右子树指针、左子树指针，我们可以考虑使用链式存储来表示二叉树。

        当我们使用数据域、左右子树指针表示二叉树的结构时，得到的二叉树链表成为二叉链表。我们还可以再二叉链表的基础上增加一个父结点的数据域，这样得到的二叉树链表称为三叉链表。

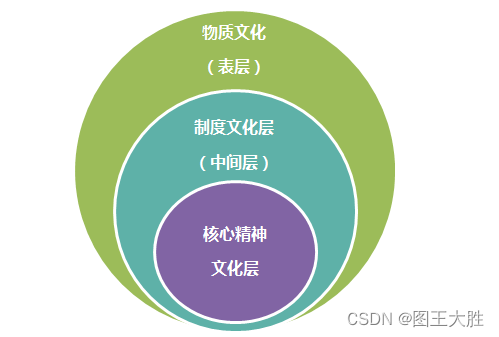
        二叉链表和三叉链表的存储结构如下图所示：

                        图1.二叉链表和三叉链表的表示                

2.二叉链表的表示和实现

1.定义

typedef char TelemType;
typedef int Status;
typedef struct BiTNode{
    TelemType data;//数据域
    struct BiTNode * lchild,*rchild;//左右孩子指针
}BiTNode,*BiTree;

2.创建

// 创建二叉树
Status createBiTree(BiTree *tree) {
    TelemType data;
    scanf("%c", &data); // 读取节点数据
    
    if (data == '#') {
        *tree = NULL; // 空节点
    } else {
        *tree = (BiTNode *)malloc(sizeof(BiTNode));
        if (!*tree) {
            exit(EXIT_FAILURE); // 内存分配失败
            return 0;
        }
        (*tree)->data = data; // 存储节点数据
        createBiTree(&((*tree)->lchild)); // 递归创建左子树
        createBiTree(&((*tree)->rchild)); // 递归创建右子树
    }
    
    return 1; // 创建成功
}

3.先序遍历二叉树

// 先序遍历二叉树
Status preOrderTraverse(BiTree tree) {
    if (tree == NULL) {
        return 1; // 空树，遍历结束
    }
    
    // 访问根节点
    printf("%c ", tree->data);
    
    // 递归遍历左子树
    preOrderTraverse(tree->lchild);
    
    // 递归遍历右子树
    preOrderTraverse(tree->rchild);
    
    return 1; // 遍历成功
}

4.中序遍历二叉树

// 中序遍历二叉树
Status inOrderTraverse(BiTree tree) {
    if (tree == NULL) {
        return 1; // 空树，遍历结束
    }
    
    // 递归遍历左子树
    inOrderTraverse(tree->lchild);
    
    // 访问根节点
    printf("%c ", tree->data);
    
    // 递归遍历右子树
    inOrderTraverse(tree->rchild);
    
    return 1; // 遍历成功
}

5.后序遍历二叉树

// 后序遍历二叉树
Status postOrderTraverse(BiTree tree) {
    if (tree == NULL) {
        return 1; // 空树，遍历结束
    }
    
    // 递归遍历左子树
    postOrderTraverse(tree->lchild);
    
    // 递归遍历右子树
    postOrderTraverse(tree->rchild);
    
    // 访问根节点
    printf("%c ", tree->data);
    
    return 1; // 遍历成功
}

6.后序遍历二叉树

// 后序遍历二叉树
Status postOrderTraverse(BiTree tree) {
    if (tree == NULL) {
        return 1; // 空树，遍历结束
    }
    
    // 递归遍历左子树
    postOrderTraverse(tree->lchild);
    
    // 递归遍历右子树
    postOrderTraverse(tree->rchild);
    
    // 访问根节点
    printf("%c ", tree->data);
    
    return 1; // 遍历成功
}

7.完整代码

#include <stdio.h>
#include <stdlib.h>

typedef char TelemType;
typedef int Status;
typedef struct BiTNode{
    TelemType data;//数据域
    struct BiTNode * lchild,*rchild;//左右孩子指针
}BiTNode,*BiTree;

// 创建二叉树
Status createBiTree(BiTree *tree) {
    TelemType data;
    scanf("%c", &data); // 读取节点数据
    
    if (data == '#') {
        *tree = NULL; // 空节点
    } else {
        *tree = (BiTNode *)malloc(sizeof(BiTNode));
        if (!*tree) {
            exit(EXIT_FAILURE); // 内存分配失败
            return 0;
        }
        (*tree)->data = data; // 存储节点数据
        createBiTree(&((*tree)->lchild)); // 递归创建左子树
        createBiTree(&((*tree)->rchild)); // 递归创建右子树
    }
    
    return 1; // 创建成功
}

// 先序遍历二叉树
Status preOrderTraverse(BiTree tree) {
    if (tree == NULL) {
        return 1; // 空树，遍历结束
    }
    
    // 访问根节点
    printf("%c ", tree->data);
    
    // 递归遍历左子树
    preOrderTraverse(tree->lchild);
    
    // 递归遍历右子树
    preOrderTraverse(tree->rchild);
    
    return 1; // 遍历成功
}

// 中序遍历二叉树
Status inOrderTraverse(BiTree tree) {
    if (tree == NULL) {
        return 1; // 空树，遍历结束
    }
    
    // 递归遍历左子树
    inOrderTraverse(tree->lchild);
    
    // 访问根节点
    printf("%c ", tree->data);
    
    // 递归遍历右子树
    inOrderTraverse(tree->rchild);
    
    return 1; // 遍历成功
}

// 后序遍历二叉树
Status postOrderTraverse(BiTree tree) {
    if (tree == NULL) {
        return 1; // 空树，遍历结束
    }
    
    // 递归遍历左子树
    postOrderTraverse(tree->lchild);
    
    // 递归遍历右子树
    postOrderTraverse(tree->rchild);
    
    // 访问根节点
    printf("%c ", tree->data);
    
    return 1; // 遍历成功
}


int main(int argc, const char *argv[]) {
    BiTree tree;
        
    printf("请输入二叉树的前序序列（使用'#'表示空节点）：\n");
    createBiTree(&tree);
    printf("二叉树创建成功！\n");
    
    printf("先序遍历二叉树..\n");
    preOrderTraverse(tree);
    printf("\n中序遍历二叉树...\n");
    inOrderTraverse(tree);
    printf("\n后序遍历二叉树...\n");
    postOrderTraverse(tree);
    printf("\n");
    return 0;
}

        例如我们要生成如下图所示的二叉树。控制台输入ABD##E##CF##G##

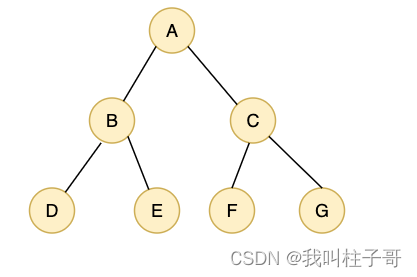
图1.测试二叉树

        控制台打印结果如下：

        OK，打印结果正确。