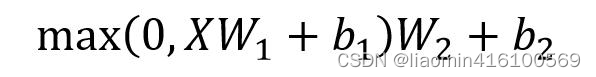前言:
本系列是学习了董晓老师所讲的知识点做的笔记
董晓算法的个人空间-董晓算法个人主页-哔哩哔哩视频 (bilibili.com)
动态规划系列
【算法】动态规划之线性DP问题-CSDN博客
【算法】动态规划之背包DP问题(2024.5.11)-CSDN博客
背包DP
背包问题方案数

f[i]表示背包容量为i时能装入物品的最大价值,c[i]表示营包容量为i时最优选法的方案数
for (int i = 0; i <= m; i++) c[i] = 1;//背包里不装入物品也是一种方案
for (int i = 1; i <= n; i++)
{
scanf("%d%d", &v, &w);
for (int j = m; j >= v; j--) {
if (f[j - v] + w > f[j]) {//容量从j-v增加到j,只是多装入一件物品,没有改变方案数c[j-v]所以c[j] = c[j-v]
f[j] = f[j - v] + w;
c[j] = c[j - v];
}
else
//不装入新物品,容量j已有的方案数为c[j];
//若装入新物品,容量j对应的方案数为c[j - v]
//两种情况,方案显然不同,所以取和。为防止爆掉int,对大数取余
c[j] = (c[j] + c[j - v]) % mod;
}
}
printf("%d\n", c[m]);背包问题求具体方案

题目要求输出字典序最小的方案,假设存在一个包含第1个物品的最优解,为了确保字典序最小那么我们必然要选第1个。那么问题就转化成从2~N这些物品中找到最优解。
首先,我们从后向前遍历物品,让最优解落在f[1][m]中;
然后,我们从f[1][m]开始搜索字典序最小的路径方案。
状态定义:f[i][j]表示从第i个物品到最后一个物品装入容量为j的背包的最优解。
状态转移:f[i][j]= max(f[i+1][j],f[i+1][j-v[i]]+ w[i])
for(int i=1; i<=n; i++) cin>>v[i]>>w[i];
for(int i=n; i>=1; i--) //逆序取物
for(int j=0; j<=m; j++){
f[i][j]=f[i+1][j];
p[i][j]=j; //记录路径列
if(j>=v[i])
f[i][j]=max(f[i][j],f[i+1][j-v[i]]+w[i]);
if(j>=v[i] && f[i][j]==f[i+1][j-v[i]]+w[i])
p[i][j]=j-v[i];//记录路径列
}
int j=m;
for(int i=1; i<=n; i++){//找路
if(p[i][j]<j){
printf("%d ",i);
j=p[i][j];
}树形DP
一般思路:
线形DP子结构是一条线段,树形DP子结构是一颗子树。从分析子树入手,最优解通常是与子树根节点u有关的函数,状态计算就是寻找根点与子节点以及边权的递推关系。
编写代码,通常要dfs,从根到叶一路深搜,再从叶到根做后序DP,每次用其子树的f值更新当前节点的f值,兜了一圈回到根节点根节点的f值就是全局最优解。
没有上司的舞会
P1352 没有上司的舞会 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

存储代码
vector<int>a[N];
cin >> x >> y;
a[y].push_back(x);核心代码
void dfs(int u) {//深搜节点+后序DP
f[u][1] = w[u];//选u的快乐指数
for (int v : a[u]) {
dfs(v);
f[u][0] += max(f[v][0], f[v][1]);//不选择根节点的话,他的子节点可选可不选(根据题意)
f[u][1] += f[v][0];//选择根节点,子节点不可以选(根据题意)
}总代码
#include<iostream>
#include<vector>
using namespace std;
const int N =6010;
int n;
int w[N];
vector<int> a[N];
bool fa[N];
int f[N][2];
void dfs(int u) {//深搜节点+后序DP
f[u][1] = w[u];//选u的快乐指数
for (int v : a[u]) {
dfs(v);
f[u][0] += max(f[v][0], f[v][1]);//不选择根节点的话,他的子节点可选可不选(根据题意)
f[u][1] += f[v][0];//选择根节点,子节点不可以选(根据题意)
}
}
int main() {
cin >> n;
for (int i = 1; i <= n; i++)
cin >> w[i];//存储快乐指数
for (int i = 0; i < n - 1; i++) {
int x, y;
cin >> x >> y;
//把y的邻接点x存入数组a
//y的邻接点个数存入b数组中去
a[y].push_back(x);
fa[x] = true;//x有父亲节点
}
int root = 1;
while (fa[root]) root++;//找根节点 如果他有父亲节点的话就说明他不是根节点
dfs(root);
cout << max(f[root][0], f[root][1]);//选择根节点或者不选择根节点
}树形背包
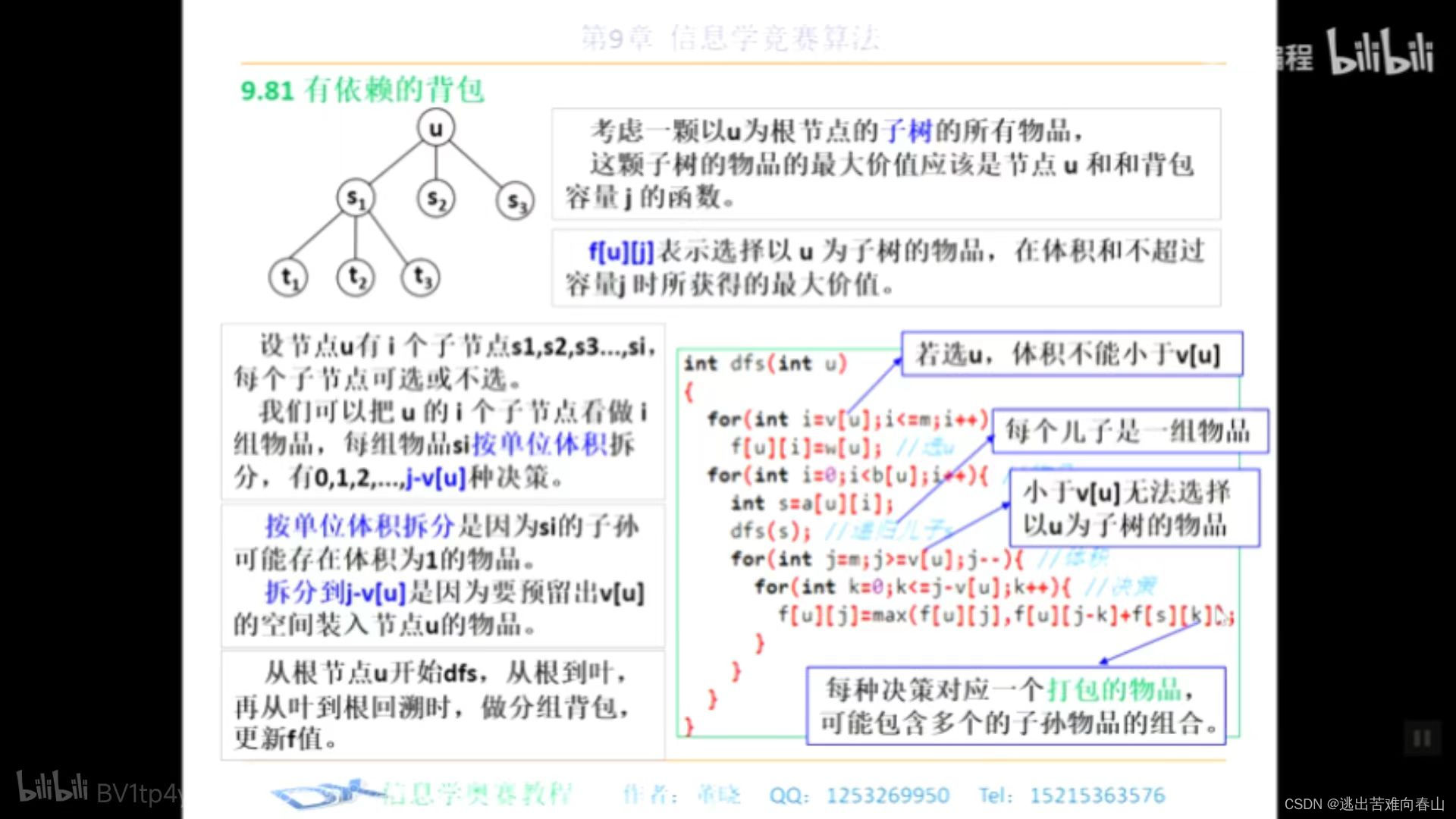
对01背包进行的改造:
f[i]表示背包容量为i时能装入物品的最大价值
c[i]表示营包容量为i时最优选法的方案数
void dfs(int u){
for(int i=v[u];i<=m;i++) f[u][i]=w[u];//如果选u的话,体积不能够小于v[u]
for(int i=0;i<b[u];i++){ //子节点
int s=a[u][i];
dfs(s);//递归儿子
for(int j=V;j>=v[u];j--) //体积
for(int k=0;k<=j-v[u];k++)//决策
f[u][j]=max(f[u][j],f[u][j-k]+f[s][k]);
}
}树的重心
重心的定义
重心是指树中的一个结点,如果将这个点删除后,剩余各个连通块中点数的最大值最小,那么这个结点被称为树的重心。
要求:
找到树的重心,并输出将重心删除后,剩余各个连通块中点数的最大值。
代码
int dfs(int u)
{
vis[u] = true;
int size = 0;//记录u的最大子树的结点数;
int sum = 1;//记录以u为根的子树的结点数:
for (int i = h[u]; i != -1; i = ne[i]) {//i是边的编号
int j = e[i];//j是u的邻接点
if (vis[j]) continue;//避免向上搜索
int s = dfs(j);//s是以j为根的字数的节点数
size = max(size, s);//记录u的最大子树的结点数
sum += s;//累加u的各个子树的结点数
}
ans = min(ans, max(size, n - sum)); //n-sum u上面的部分的结点数:
return sum;
}树的最长路径
找到一条路径,使得路径两端点的距离最远。
思路:找到从根节点向下走的最长路径和次长路径加起来
int dfs(int u)
{
vis[u] = true;
int d1 = 0;//最长
int d2 = 0;//次长
for (int i = h[u]; i != -1; i = ne[i]) {
int j = e[i];//j是u的临界点
if (vis[j]) continue;
int d = dfs(j) + w[i];//从u经过j点往下走的最大长度
if (d >= d1)//比最长还要长
{
d2 = d1;
d1 = d;
}
else if (d > d2) {
d2 = d;
}
}
ans = max(ans, d1 + d2);
return ans;
}
树的中心
定义
该点到树中其他点的最远距离最近
思路
分类处理