1.按摩师
按摩师

思路:

class Solution {
public:
int massage(vector<int>& nums) {
//创建dp表
//初始化
//填表
//返回值
int n = nums.size();
if(n == 0) return 0;
vector<int> f(n);
auto g = f;
f[0] = nums[0];
for(int i = 1; i < n; i++)
{
f[i] = g[i - 1] + nums[i];
g[i] = max(f[i - 1], g[i - 1]);
}
return max(f[n - 1], g[n - 1]);
}
};2.打家劫舍ii
打家劫舍ii

思路:
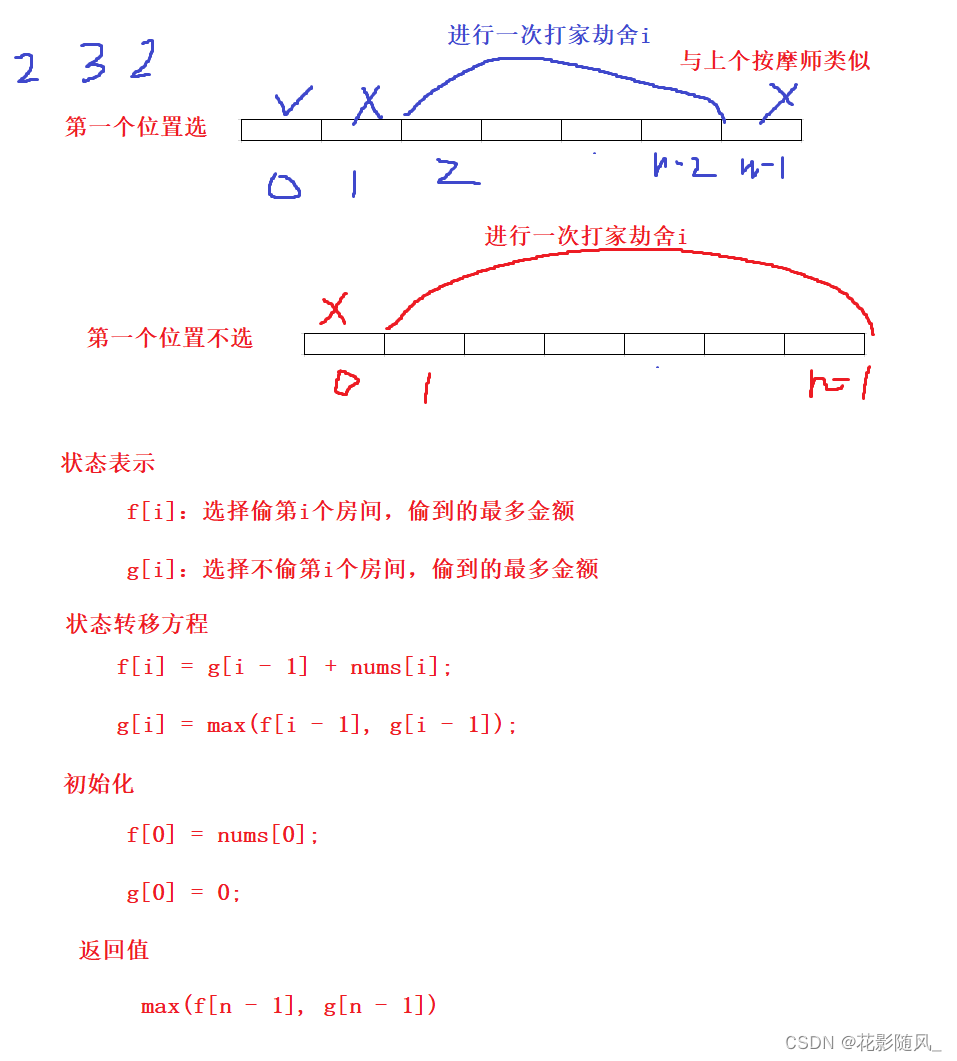
class Solution {
public:
int rob(vector<int>& nums) {
int n = nums.size();
return max(nums[0] + rob1(nums, 2, n - 2), rob1(nums, 1, n - 1));
}
int rob1(vector<int>& nums, int left, int right)
{
//处理细节问题
if(left > right) return 0;
//创建dp表
//初始化
//填表顺序
//返回值
vector<int> f(nums.size());
auto g = f;
f[left] = nums[left];
for(int i = left + 1; i <= right; i++)
{
f[i] = g[i - 1] + nums[i];
g[i] = max(f[i - 1], g[i - 1]);
}
return max(f[right], g[right]);
}
};3.删除并获得点数
删除并获得点数

思路:

class Solution {
public:
int deleteAndEarn(vector<int>& nums) {
const int N = 10001;
//创建一个大小10001新数组
int arr[N] = {0};
//填充arr数组
for(auto x : nums)
arr[x] += x;
//创建dp表
//初始化
//填表
//返回值
vector<int> f(N);
auto g = f;
for(int i = 1; i < N; i++)
{
f[i] = g[i - 1] + arr[i];
g[i] = max(f[i - 1], g[i - 1]);
}
return max(f[N - 1], g[N - 1]);
}
};4.粉刷房子
粉刷房子

思路:

class Solution {
public:
int minCost(vector<vector<int>>& costs) {
//创建dp表
//初始化
//填表
//返回值
int n = costs.size();
vector<vector<int>> dp(n + 1, vector<int>(3));
for(int i = 1; i <= n; i++)
{
dp[i][0] = min(dp[i - 1][1], dp[i - 1][2]) + costs[i - 1][0];
dp[i][1] = min(dp[i - 1][0], dp[i - 1][2]) + costs[i - 1][1];
dp[i][2] = min(dp[i - 1][0], dp[i - 1][1]) + costs[i - 1][2];
}
return min(dp[n][0], min(dp[n][1], dp[n][2]));
}
};5.买卖股票的最佳时机含冷冻期
买卖股票的最佳时机含冷冻期

思路:
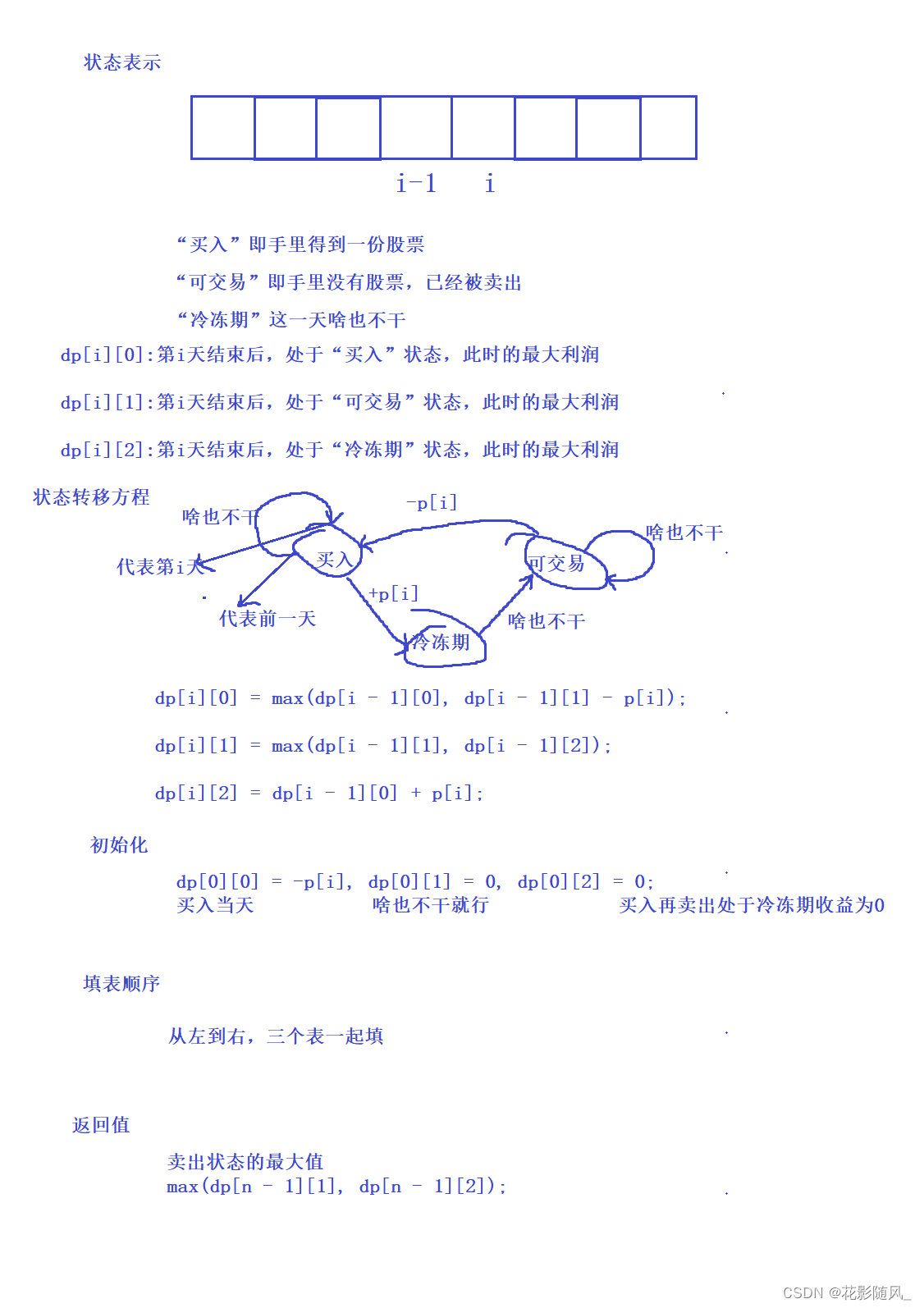
class Solution {
public:
int maxProfit(vector<int>& prices) {
//创建dp表
//初始化
//填表
//返回结果
int n = prices.size();
vector<vector<int>> dp(n, vector<int>(3));
dp[0][0] = -prices[0];
for(int i = 1; i < n; i++)
{
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
dp[i][1] = max(dp[i - 1][1], dp[i - 1][2]);
dp[i][2] = dp[i - 1][0] + prices[i];
}
return max(dp[n - 1][1], dp[n - 1][2]);
}
};6.买卖股票的最佳时机含手续费
买卖股票的最佳时机含手续费

思路:

class Solution {
public:
int maxProfit(vector<int>& prices, int fee) {
//创建dp表
//初始化
//填表
//返回结果
int n = prices.size();
vector<int> f(n);
auto g = f;
f[0] = -prices[0];
for(int i = 1; i < n; i++)
{
f[i] = max(f[i - 1], g[i - 1] - prices[i]);
g[i] = max(f[i - 1] + prices[i] - fee, g[i - 1]);
}
return g[n - 1];
}
};7.买卖股票的最佳时机iii
买卖股票的最佳时机iii

思路:

class Solution {
public:
int maxProfit(vector<int>& prices) {
const int INF = 0x3f3f3f3f;
//创建dp表
//初始化
//填表
//返回结果
int n = prices.size();
vector<vector<int>> f(n, vector<int>(3, -INF));
auto g = f;
f[0][0] = -prices[0];
g[0][0] = 0;
for(int i = 1; i < n; i++)
{
for(int j = 0; j < 3; j++)
{
f[i][j] = max(f[i - 1][j], g[i - 1][j] - prices[i]);
g[i][j] = g[i - 1][j];
if(j >= 1)
g[i][j] = max(g[i][j], f[i - 1][j - 1] + prices[i]);
}
}
int ret = 0;
for(int i = 0; i < 3; i++)
{
ret = max(ret, g[n - 1][i]);
}
return ret;
}
};
8.买卖股票的最佳时机iv
买卖股票的最佳时机iv

思路:
与 买卖股票的最佳时机iii是完全类似的只需要把j次变为k次就可
class Solution {
public:
int maxProfit(int k, vector<int>& prices) {
const int INF = 0x3f3f3f3f;
//创建dp表
//初始化
//填表
//返回结果
int n = prices.size();
//处理细节问题
k = min(k, n / 2);
vector<vector<int>> f(n, vector<int>(k + 1, -INF));
auto g = f;
f[0][0] = -prices[0];
g[0][0] = 0;
for(int i = 1; i < n; i++)
{
for(int j = 0; j <= k; j++)
{
f[i][j] = max(f[i - 1][j], g[i - 1][j] - prices[i]);
g[i][j] = g[i - 1][j];
if(j >= 1)
g[i][j] = max(g[i][j], f[i - 1][j - 1] + prices[i]);
}
}
int ret = 0;
for(int i = 0; i <= k; i++)
{
ret = max(ret, g[n - 1][i]);
}
return ret;
}
};