在数据挖掘和机器学习领域,TPR(True Positive Rate)是指在实际为阳性的情况下,模型正确预测为阳性的比例。TPR也被称为灵敏度(Sensitivity)或召回率(Recall)。它是评估分类模型性能的一个重要指标,尤其是在不平衡数据集的情况下。
TPR的计算公式如下:

- TP(True Positive)是指模型正确预测为阳性的数量。
- FN(False Negative)是指模型错误预测为阴性的实际阳性数量。
TPR的范围从0到1,值越高表示模型的性能越好,即模型能够更好地识别出实际的阳性样本。在有些应用中,如疾病筛查或欺诈检测,我们通常希望模型有较高的TPR,以减少漏诊或漏检的情况。
与TPR相关的另一个指标是FPR(False Positive Rate),它是指在实际为阴性的情况下,模型错误预测为阳性的比例。TPR和FPR通常一起用于绘制ROC(Receiver Operating Characteristic)曲线,这是一种评估分类模型性能的图形化工具。
在数据挖掘和机器学习领域,TPR(True Positive Rate)是指在实际为阳性的情况下,模型正确预测为阳性的比例。TPR也被称为灵敏度(Sensitivity)或召回率(Recall)。它是评估分类模型性能的一个重要指标,尤其是在不平衡数据集的情况下。
TPR的计算公式如下:

其中:
- TP(True Positive)是指模型正确预测为阳性的数量。
- FN(False Negative)是指模型错误预测为阴性的实际阳性数量。
TPR的范围从0到1,值越高表示模型的性能越好,即模型能够更好地识别出实际的阳性样本。在有些应用中,如疾病筛查或欺诈检测,我们通常希望模型有较高的TPR,以减少漏诊或漏检的情况。
与TPR相关的另一个指标是FPR(False Positive Rate),它是指在实际为阴性的情况下,模型错误预测为阳性的比例。TPR和FPR通常一起用于绘制ROC(Receiver Operating Characteristic)曲线,这是一种评估分类模型性能的图形化工具。
在数据挖掘和机器学习领域,TNR(True Negative Rate)是指在实际为阴性的情况下,模型正确预测为阴性的比例。TNR也被称为特异性(Specificity)。它是评估分类模型性能的另一个重要指标,尤其是在需要严格控制假阳性(错误地预测为阳性)的应用场景中。
TNR的计算公式如下:

其中:
- TN(True Negative)是指模型正确预测为阴性的数量。
- FP(False Positive)是指模型错误预测为阳性的实际阴性数量。
TNR的范围同样从0到1,值越高表示模型的特异性越好,即模型在识别阴性样本方面的能力越强。在一些医学检测、安检和金融风控等领域,减少假阳性结果非常重要,因此TNR是一个关键的评估指标。
与TNR相关的另一个指标是TPR(True Positive Rate),它是指在实际为阳性的情况下,模型正确预测为阳性的比例。TNR和TPR通常一起考虑,以全面评估模型的性能。在ROC(Receiver Operating Characteristic)曲线中,TNR以FPR(False Positive Rate)的补数形式表示,即:

ROC曲线是基于TPR和FPR绘制的,它可以帮助我们理解模型在不同阈值设置下的性能表现。
在数据挖掘和机器学习领域,FPR(False Positive Rate)是指在实际为阴性的情况下,模型错误预测为阳性的比例。FPR也被称为假阳性率,它是评估分类模型性能的一个重要指标,特别是在需要控制错误拒绝(即错误地将阴性样本判定为阳性)的应用场景中。
FPR的计算公式如下:
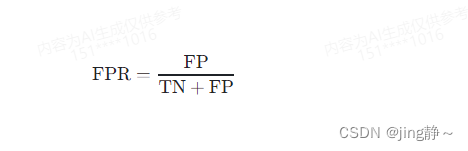
其中:
- FP(False Positive)是指模型错误预测为阳性的实际阴性数量。
- TN(True Negative)是指模型正确预测为阴性的数量。
FPR的范围从0到1,值越低表示模型的特异性越好,即模型在避免将阴性样本错误分类为阳性方面的能力越强。在医学检测、安检和金融风控等领域,降低假阳性结果非常重要,因此FPR是一个关键的评估指标。
与FPR相关的另一个指标是TPR(True Positive Rate),它是指在实际为阳性的情况下,模型正确预测为阳性的比例。FPR和TPR通常一起考虑,以全面评估模型的性能。在ROC(Receiver Operating Characteristic)曲线中,FPR作为横轴,而TPR作为纵轴,它可以帮助我们理解模型在不同阈值设置下的性能表现。
在数据挖掘和机器学习领域,FNR(False Negative Rate)是指在实际为阳性的情况下,模型错误预测为阴性的比例。FNR也被称为漏诊率(Miss Rate),它是评估分类模型性能的一个重要指标,特别是在需要尽量避免遗漏阳性样本的应用场景中。
FNR的计算公式如下:

其中:
- FN(False Negative)是指模型错误预测为阴性的实际阳性数量。
- TP(True Positive)是指模型正确预测为阳性的数量。
FNR的范围从0到1,值越低表示模型的敏感性越好,即模型在识别阳性样本方面的能力越强。在疾病诊断、欺诈检测等应用中,减少漏诊或漏检的情况非常关键,因此FNR是一个重要的性能指标。
与FNR相关的另一个指标是TNR(True Negative Rate),它是指在实际为阴性的情况下,模型正确预测为阴性的比例。FNR和TNR通常一起考虑,以全面评估模型的性能。在ROC(Receiver Operating Characteristic)曲线中,FNR以TNR的补数形式表示,即:
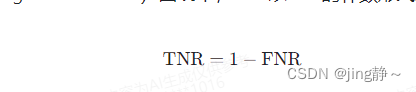
ROC曲线是基于TPR和FPR(FPR是FNR的补数)绘制的,它可以帮助我们理解模型在不同阈值设置下的性能表现。
决策树是一种常用的机器学习算法,用于分类和回归任务。它是一种树形结构,其中每个内部节点代表一个特征或属性,每个分支代表一个特征值,每个叶节点代表一个类别标签。一个决策树通常包含以下要素:
1. **根节点**:决策树的顶部节点,代表整个数据集,是决策过程的起点。
2. **内部节点**:决策树中的决策点,每个内部节点都基于一个特征来分割数据集。内部节点通常会有两个或更多的分支,每个分支代表一个可能的特征值。
3. **分支**:连接内部节点和其子节点的连线,代表特征的某个具体值。数据集根据分支上的特征值被分割成子集。
4. **叶节点**:决策树的底部节点,也称为终端节点或叶子节点。每个叶节点代表一个类标签(在分类树中)或一个预测值(在回归树中)。
5. **特征选择**:在构建决策树时,选择哪个特征作为内部节点的依据是一个关键步骤。不同的特征选择标准(如信息增益、增益率、基尼不纯度等)会导致不同的树结构。
6. **分割标准**:决策树算法使用分割标准来决定如何在内部节点分割数据集。常用的分割标准包括信息增益、增益率和基尼不纯度等。
7. **剪枝策略**:为了防止过拟合,决策树可能会通过剪枝来简化模型。剪枝可以分为预剪枝(在树生长过程中提前停止生长)和后剪枝(在树完全生长后删除不必要的节点)。
8. **树的深度**:决策树的深度是指从根节点到叶节点的最长路径。树的深度影响模型的复杂度和泛化能力。
9. **子树**:每个内部节点的子节点可以看作是一个子树,它包含了该节点下的所有分支和叶节点。
10. **纯度**:决策树的目标是创建纯度高的叶节点,即叶节点中尽量属于同一类别的数据。纯度可以通过熵、基尼不纯度等指标来衡量。