Java常见数据结构---八大结构

news2024/11/29 20:31:04

  前言：

数据结构是计算机底层存储、组织数据的方式。是指数据相互之间是以什么方式排列在一起的。 通常情况下，精心选择的数据结构可以带来更高的运行或者存储效率 

常见的八大数据结构：

 栈：

思想：

栈是一种数据结构，它遵循后进先出 (LIFO) 原则。这意味着最后添加的元素（称为栈顶元素）将首先被移除。

特点：

  • **简单性和效率：**栈的操作（push、pop、peek）可以在常数时间内完成。
  • **后进先出：**栈的 LIFO 特性使其非常适合需要按添加顺序处理元素的应用。
  • 可以理解为子弹夹一样，先进后出，后出先进

 

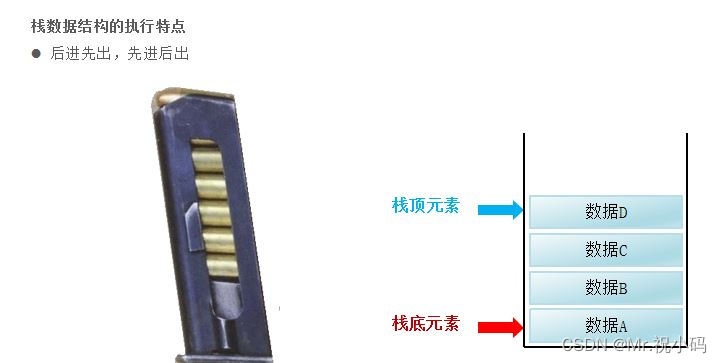
 数据进入栈模型的过程称为：压/进栈

  数据出栈模型的过程称为：弹/出栈

代码： 

public class Stack {

    private int[] arr;
    private int top;
    private int capacity;

    public Stack(int capacity) {
        this.arr = new int[capacity];
        this.top = -1;
        this.capacity = capacity;
    }

    public void push(int element) {
        if (isFull()) {
            System.out.println("Stack overflow");
            return;
        }

        arr[++top] = element;
    }

    public int pop() {
        if (isEmpty()) {
            System.out.println("Stack underflow");
            return -1;
        }

        return arr[top--];
    }

    public int peek() {
        if (isEmpty()) {
            System.out.println("Stack is empty");
            return -1;
        }

        return arr[top];
    }

    public boolean isEmpty() {
        return top == -1;
    }

    public boolean isFull() {
        return top == capacity - 1;
    }

    public static void main(String[] args) {
        Stack stack = new Stack(5);

        stack.push(1);
        stack.push(2);
        stack.push(3);
        stack.push(4);

        System.out.println("Top element: " + stack.peek());

        stack.pop();
        stack.pop();

        System.out.println("Top element: " + stack.peek());
    }
}

过程：

过程解释：

  1. 创建栈：我们创建一个容量为 5 的栈对象。栈是用数组实现的，其中 top 变量跟踪栈顶元素的索引。
  2. 压入元素：push 方法将元素压入栈中。如果栈已满，它会打印一条错误消息。
  3. 弹出元素：pop 方法从栈中移除并返回栈顶元素。如果栈为空，它会打印一条错误消息。
  4. 查看栈顶元素：peek 方法返回栈顶元素，但不将其移除。如果栈为空，它会打印一条错误消息。
  5. 检查栈是否为空：isEmpty 方法检查栈是否为空。
  6. 检查栈是否已满：isFull 方法检查栈是否已满。
  7. 主方法：**在主方法中，我们创建了一个栈对象，压入一些元素，弹出一些元素，并打印栈顶元素。

 最后输出：

Top element: 4

Top element: 2

 

队列：

思想：

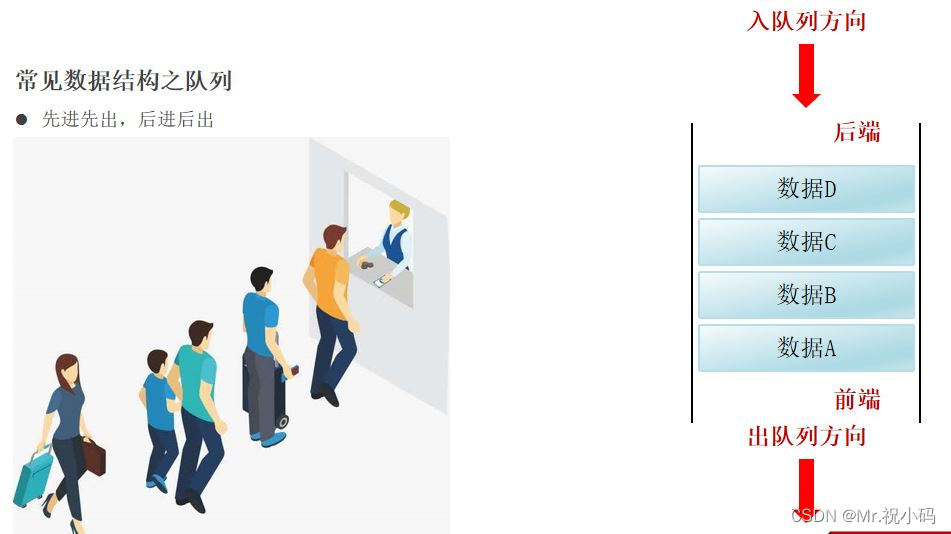
队列是一种遵循先进先出 (FIFO) 原则的数据结构。这意味着队列中的第一个添加的元素将首先被移除。与栈恰恰相反，队列两端全开，遵循先进先出，后进后出的原则

特点：

  • 先进先出 (FIFO)：队列遵循先进先出原则，这意味着第一个添加的元素将首先被移除。
  • 线性数据结构：队列是一种线性数据结构，这意味着元素按顺序排列。
  • 插入在末尾：新元素总是添加到队列的末尾（也称为尾部）。
  • 删除在头部：元素从队列的头部（也称为前端）移除。
  • 限制访问：队列只允许在头部和尾部进行插入和删除操作。中间元素无法直接访问。
  • 队列大小：队列可以是固定大小的（使用数组实现）或动态大小的（使用链表实现）。
  • 广泛的应用：队列在计算机科学中有广泛的应用，例如消息传递、任务调度、缓冲和广度优先搜索

  

代码： 

import java.util.LinkedList;
import java.util.Queue;

public class QueueExample {

    public static void main(String[] args) {
        // 创建一个队列
        Queue<Integer> queue = new LinkedList<>();

        // 向队列中添加元素
        queue.add(1);
        queue.add(2);
        queue.add(3);
        queue.add(4);

        // 从队列中移除元素
        int removedElement = queue.remove(); // 移除并返回第一个元素

        // 查看队列中的第一个元素
        int headElement = queue.peek(); // 返回第一个元素，但不将其移除

        // 检查队列是否为空
        boolean isEmpty = queue.isEmpty();

        // 打印队列中的元素
        System.out.println("Queue elements: " + queue);

        // 打印移除的元素
        System.out.println("Removed element: " + removedElement);

        // 打印队列头部的元素
        System.out.println("Head element: " + headElement);

        // 打印队列是否为空
        System.out.println("Queue is empty: " + isEmpty);
    }
}

输出：

Queue elements: [2, 3, 4]
Removed element: 1
Head element: 2
Queue is empty: false

过程： 

  1. 创建队列：我们使用 Java 的 LinkedList 类创建一个队列。LinkedList 实现了 Queue 接口，它提供了队列的基本操作。
  2. 添加元素：add 方法将元素添加到队列的末尾。
  3. 移除元素：remove 方法从队列中移除并返回第一个元素。
  4. 查看队列头部的元素：peek 方法返回队列中的第一个元素，但不将其移除。
  5. 检查队列是否为空：isEmpty 方法检查队列是否为空。

数组：

思想：

数组是一种数据结构，它存储固定数量的相同类型元素的集合。数组中的元素使用索引进行访问，索引从 0 开始。

数组相对其他数据结构相对来说比较简单理解，可以理解为是一组元素，起始值下标从0开始

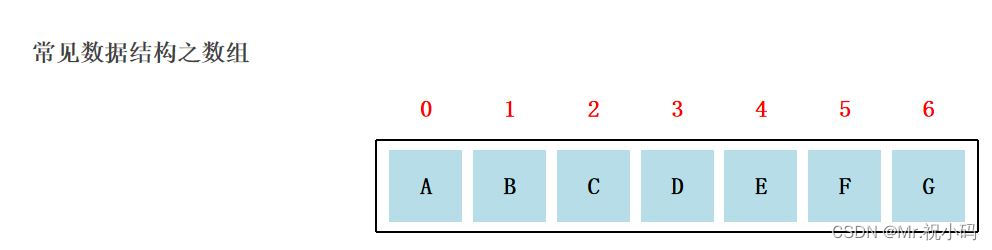
  1. 查询速度快：查询数据通过地址值和索引定位，查询任意数据耗时相同。 
  2. 删除效率低：要将原始数据删除，同时后面每个数据前移。 

代码： 

public class Array {

    public static void main(String[] args) {
        // 声明一个长度为 7 的整型数组
        int[] arr = {1, 2, 3, 4, 5, 6, 7};

        // 遍历数组并打印每个元素
        for (int element : arr) {
            System.out.println(element);
        }
    }
}

 过程：

  1. 声明数组：我们声明一个长度为 7 的整型数组，并使用花括号初始化其元素。
  2. 遍历数组：使用增强 for 循环遍历数组并打印每个元素。

链表：

思想：

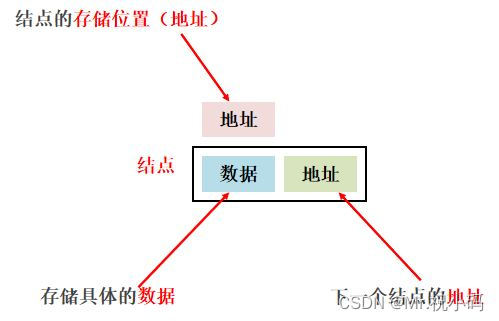
链表是一种数据结构，它由一组称为节点的对象组成。每个节点包含一个数据项和指向下一个节点的引用。

在 Java 中，链表使用以下类实现：

  • LinkedList：一个双向链表，允许在列表的任何位置添加和删除元素。
  • ArrayList：一个基于数组的列表，在列表末尾添加和删除元素非常高 

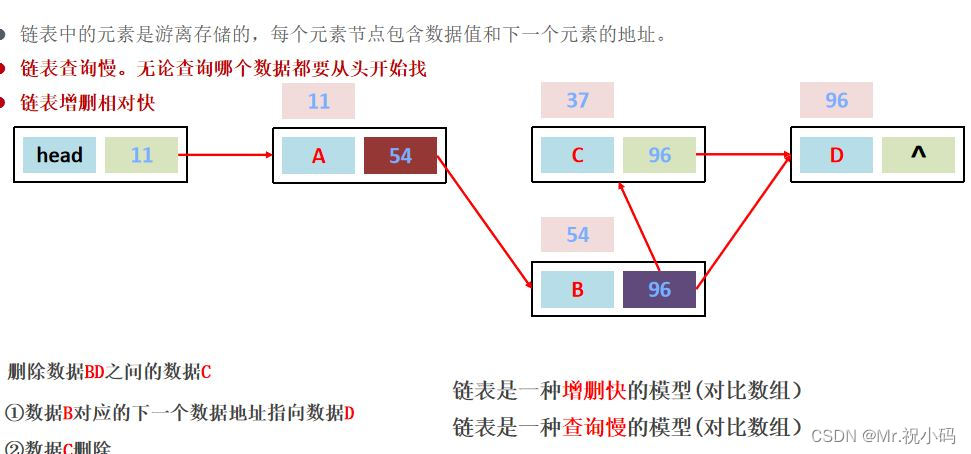
链表中的元素是游离存储的，每个元素节点包含数据值和下一个元素的地址。 

链表是一种增删快、查询慢的模型(对比数组）

 

 代码：



public class LinkedList {

    public static void main(String[] args) {
        // 创建一个链表
        LinkedList<String> list = new LinkedList<>();

        // 向链表中添加元素
        list.add("Apple");
        list.add("Banana");
        list.add("Orange");

        // 遍历链表并打印每个元素
        for (String fruit : list) {
            System.out.println(fruit);
        }

        // 从链表中删除元素
        list.remove("Banana");

        // 打印修改后的链表
        System.out.println("Modified list:");
        for (String fruit : list) {
            System.out.println(fruit);
        }
    }
}

输出：

Modified list:Apple  Orange

Banana元素已经被链表删除

二叉树：

思想：

二叉树（Binary tree）是树形结构的一个重要类型。许多实际问题抽象出来的数据结构往往是二叉树形式，即使是一般的树也能简单地转换为二叉树，而且二叉树的存储结构及其算法都较为简单，因此二叉树显得特别重要。二叉树特点是每个节点最多只能有两棵子树，且有左右之分 [1]。

特点：

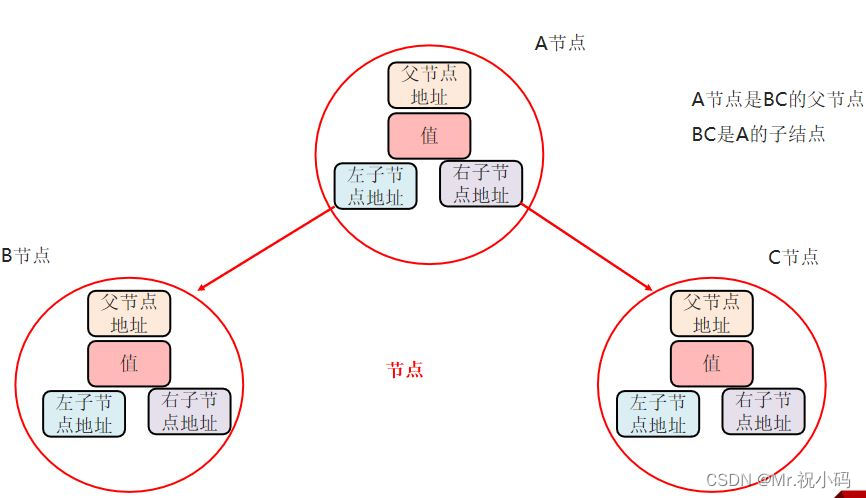
 只能有一个根节点，每个节点最多支持2个直接子节点。

节点的度： 节点拥有的子树的个数，二叉树的度不大于2 叶子节点 度为0的节点，也称之为终端结点。

高度：叶子结点的高度为1，叶子结点的父节点高度为2，以此类推，根节点的高度最高。

层：根节点在第一层，以此类推

兄弟节点 ：拥有共同父节点的节点互称为兄弟节点

代码：

 

public class BinaryTree {

    private Node root;

    public void add(int data) {
        root = addRecursive(root, data);
    }

    private Node addRecursive(Node current, int data) {
        if (current == null) {
            return new Node(data);
        }

        if (data < current.data) {
            current.left = addRecursive(current.left, data);
        } else if (data > current.data) {
            current.right = addRecursive(current.right, data);
        }

        return current;
    }

    public boolean contains(int data) {
        return containsRecursive(root, data);
    }

    private boolean containsRecursive(Node current, int data) {
        if (current == null) {
            return false;
        }

        if (data == current.data) {
            return true;
        } else if (data < current.data) {
            return containsRecursive(current.left, data);
        } else {
            return containsRecursive(current.right, data);
        }
    }

    public static void main(String[] args) {
        BinaryTree tree = new BinaryTree();
        tree.add(10);
        tree.add(5);
        tree.add(15);

        System.out.println("Contains 5: " + tree.contains(5));
        System.out.println("Contains 12: " + tree.contains(12));
    }
}

class Node {
    int data;
    Node left;
    Node right;

    public Node(int data) {
        this.data = data;
    }
}

 过程：

  1. 添加元素：add() 方法使用递归将元素添加到二叉树中。它将新元素与当前节点进行比较，并将其添加到左子树或右子树中，具体取决于元素的值。
  2. 查找元素：contains() 方法使用递归在二叉树中查找元素。它将查找值与当前节点进行比较，并根据需要递归地遍历左子树或右子树。
  3. 主方法：main() 方法创建二叉树并向其中添加元素。然后，它调用 contains() 方法来查找树中是否存在特定值。
  4. 输出：Contains 5: true Contains 12: false

二叉查找树：

思想：

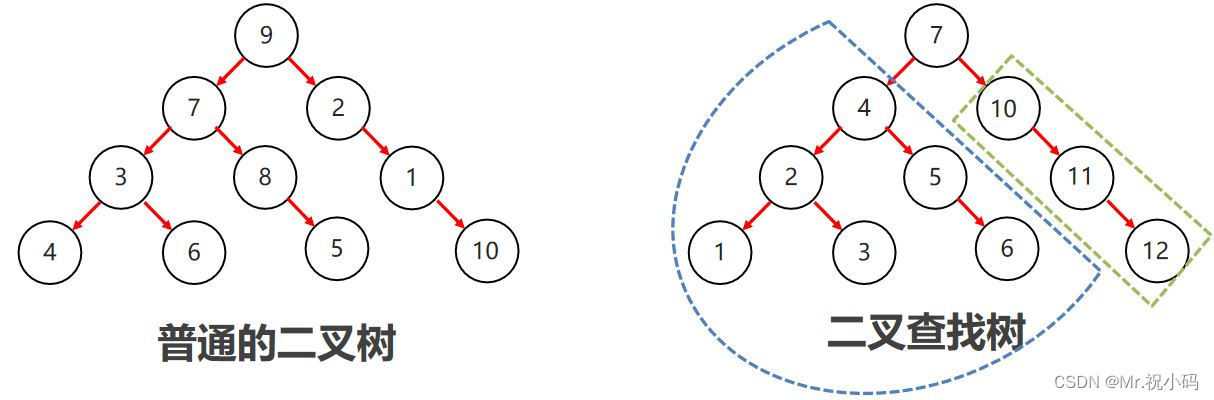
二叉搜索树又被称为排序树，它或者是一颗空树，或者是一棵具有以下性质的二叉树： 若它的左子树不为空，则左子树上所有节点的值都小于根节点的值 若它的右子树不为空，则右子树上所有节点的值都大于根节点的值

 特点：

1，每一个节点上最多有两个子节点

2，左子树上所有节点的值都小于根节点的值

3，右子树上所有节点的值都大于根节点的值 

目的：提高检索数据的性能。

不同点：

二叉树

  • 每个节点最多有两个子节点（左子节点和右子节点）。
  • 没有排序规则。
  • 可以用于表示各种数据结构，例如堆和哈夫曼树。

二叉搜索树（BST）

  • 一个特殊的二叉树，其中每个节点的值都比其左子树的所有值大，并且比其右子树的所有值小。
  • 具有以下性质：
    • 左子树中的所有值都小于根节点的值。
    • 右子树中的所有值都大于根节点的值。
    • 左子树和右子树都是二叉搜索树。

区别

二叉搜索树和二叉树之间的主要区别在于排序规则：

  • 二叉树没有排序规则，而二叉搜索树中的节点根据其值进行排序。

代码： 

public class BinarySearchTree {

    private Node root;

    public void add(int data) {
        root = addRecursive(root, data);
    }

    private Node addRecursive(Node current, int data) {
        if (current == null) {
            return new Node(data);
        }

        if (data < current.data) {
            current.left = addRecursive(current.left, data);
        } else if (data > current.data) {
            current.right = addRecursive(current.right, data);
        }

        return current;
    }

    public boolean contains(int data) {
        return containsRecursive(root, data);
    }

    private boolean containsRecursive(Node current, int data) {
        if (current == null) {
            return false;
        }

        if (data == current.data) {
            return true;
        } else if (data < current.data) {
            return containsRecursive(current.left, data);
        } else {
            return containsRecursive(current.right, data);
        }
    }

    public static void main(String[] args) {
        BinarySearchTree tree = new BinarySearchTree();
        tree.add(10);
        tree.add(5);
        tree.add(15);

        System.out.println("Contains 5: " + tree.contains(5));
        System.out.println("Contains 12: " + tree.contains(12));
    }
}

class Node {
    int data;
    Node left;
    Node right;

    public Node(int data) {
        this.data = data;
    }
}

 过程：

 

  1. 添加元素：add() 方法使用递归将元素添加到二叉查找树中。它将新元素与当前节点进行比较，并将其添加到左子树或右子树中，具体取决于元素的值。
  2. 查找元素：contains() 方法使用递归在二叉查找树中查找元素。它将查找值与当前节点进行比较，并根据需要递归地遍历左子树或右子树。
  3. 主方法：main() 方法创建二叉查找树并向其中添加元素。然后，它调用 contains() 方法来查找树中是否存在特定值

输出：

Contains 5: true
Contains 12: false

平衡二叉树：

思想：

平衡二叉树是一种特殊的二叉搜索树，其中每个节点的左子树和右子树的高度差至多为 1。这确保了树在很大程度上保持平衡，并且查找、插入和删除操作的时间复杂度为 O(log n)，其中 n 是树中的节点数。

 平衡二叉树可以通过使用称为旋转的操作来实现。旋转是重新排列树中节点以维护平衡的一种方法。AVL 树和红黑树使用不同的旋转规则来保持平衡。

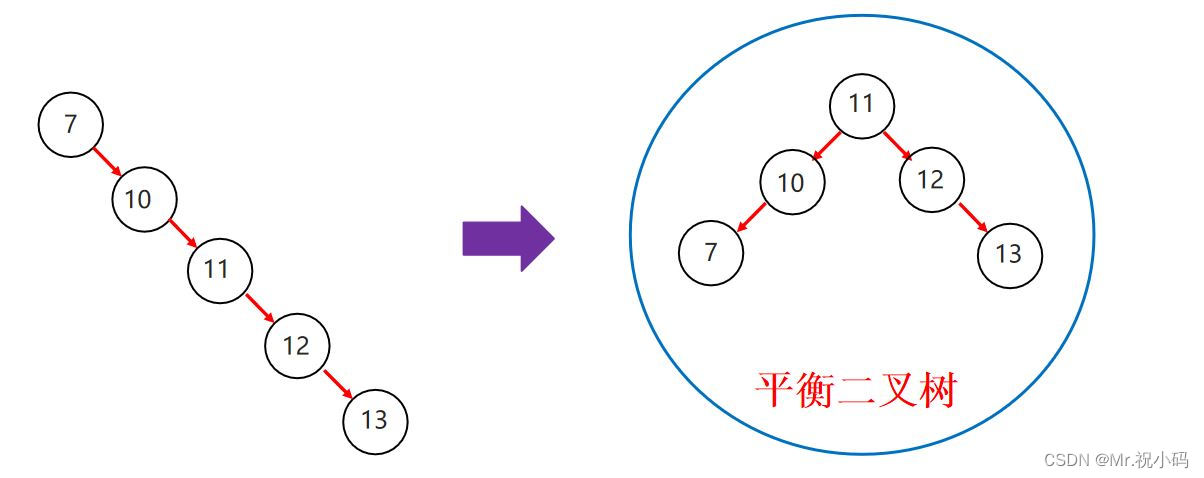
平衡二叉树是在满足查找二叉树的大小规则下，让树尽可能矮小，以此提高查数据的性能。  

代码： 

public class AVLTree {

    private Node root;

    public void add(int data) {
        root = addRecursive(root, data);
    }

    private Node addRecursive(Node current, int data) {
        if (current == null) {
            return new Node(data);
        }

        if (data < current.data) {
            current.left = addRecursive(current.left, data);
        } else if (data > current.data) {
            current.right = addRecursive(current.right, data);
        }

        updateHeight(current);
        return balance(current);
    }

    private Node balance(Node current) {
        int balanceFactor = getBalanceFactor(current);

        if (balanceFactor > 1) {
            if (getBalanceFactor(current.left) < 0) {
                current.left = leftRotate(current.left);
            }
            return rightRotate(current);
        } else if (balanceFactor < -1) {
            if (getBalanceFactor(current.right) > 0) {
                current.right = rightRotate(current.right);
            }
            return leftRotate(current);
        }

        return current;
    }

    private int getBalanceFactor(Node node) {
        if (node == null) {
            return 0;
        }
        return height(node.left) - height(node.right);
    }

    private int height(Node node) {
        if (node == null) {
            return 0;
        }
        return node.height;
    }

    private void updateHeight(Node node) {
        node.height = 1 + Math.max(height(node.left), height(node.right));
    }

    private Node leftRotate(Node node) {
        Node newRoot = node.right;
        node.right = newRoot.left;
        newRoot.left = node;

        updateHeight(node);
        updateHeight(newRoot);

        return newRoot;
    }

    private Node rightRotate(Node node) {
        Node newRoot = node.left;
        node.left = newRoot.right;
        newRoot.right = node;

        updateHeight(node);
        updateHeight(newRoot);

        return newRoot;
    }

    public static void main(String[] args) {
        AVLTree tree = new AVLTree();
        tree.add(10);
        tree.add(5);
        tree.add(15);

        System.out.println("Inorder traversal of the AVL tree:");
        inorderTraversal(tree.root);
    }

    private static void inorderTraversal(Node node) {
        if (node != null) {
            inorderTraversal(node.left);
            System.out.print(node.data + " ");
            inorderTraversal(node.right);
        }
    }
}

class Node {
    int data;
    Node left;
    Node right;
    int height;

    public Node(int data) {
        this.data = data;
        this.height = 1;
    }
}

过程： 

  1. 添加元素：add() 方法使用递归将元素添加到 AVL 树中。它将新元素与当前节点进行比较，并将其添加到左子树或右子树中，具体取决于元素的值。添加后，它更新节点的高度并平衡树以保持 AVL 性质。
  2. 平衡树：balance() 方法检查节点的平衡因子并执行必要的旋转以平衡树。
  3. 获取平衡因子：getBalanceFactor() 方法计算节点的平衡因子，它等于左子树的高度减去右子树的高度。
  4. 获取高度：height() 方法计算节点的高度，它等于其子树中最大高度加 1。
  5. 更新高度：updateHeight() 方法更新节点的高度，它等于其子树中最大高度加 1。
  6. 左旋转：leftRotate() 方法执行左旋转操作，它将当前节点的右子树作为新根，并将当前节点作为新根的左子树。
  7. 右旋转：rightRotate() 方法执行右旋转操作，它将当前节点的左子树作为新根，并将当前节点作为新根的右子树。
  8. 主方法：main() 方法创建 AVL 树并向其中添加元素。然后，它打印树的中序遍历以显示树的顺序。

结果： 

Inorder traversal of the AVL tree:
5 10 15
 

红黑树：

规则： 

 每一个节点或是红色的，或者是黑色的，根节点必须是黑色。

如果某一个节点是红色，那么它的子节点必须是黑色(不能出现两个红色节点相连的情况)。

对每一个节点，从该节点到其所有后代叶节点的简单路径上，均包含相同数目的黑色节点。

 

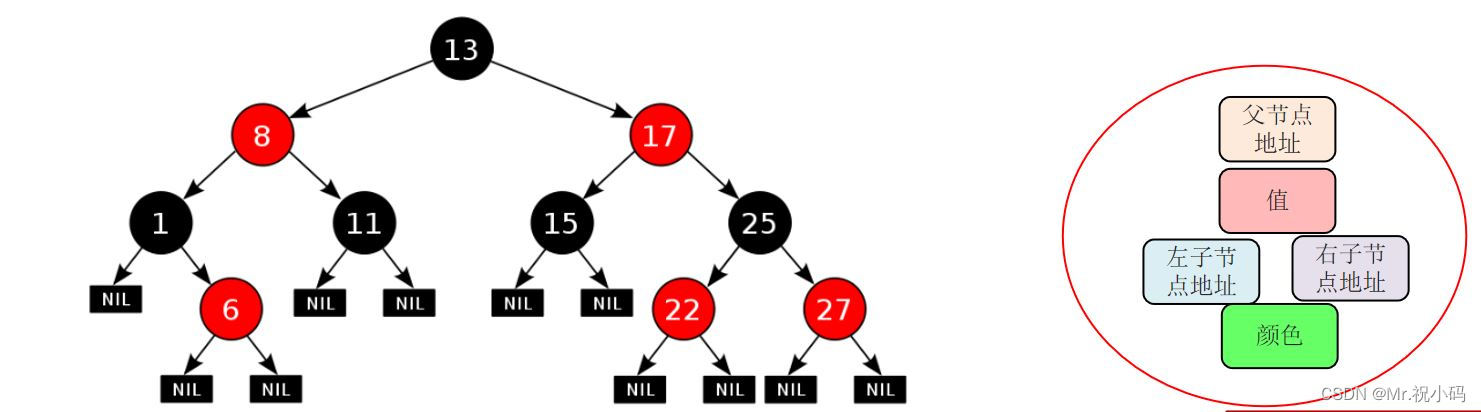
当添加的节点为根节点时，直接变成黑色就可以了 

 

 代码：

import java.util.ArrayList;
import java.util.List;

public class RedBlackTree {

    private Node root;

    public void add(int data) {
        root = addRecursive(root, data);
        root.color = Color.BLACK;
    }

    private Node addRecursive(Node current, int data) {
        if (current == null) {
            return new Node(data);
        }

        if (data < current.data) {
            current.left = addRecursive(current.left, data);
        } else if (data > current.data) {
            current.right = addRecursive(current.right, data);
        }

        if (isRed(current.left) && isRed(current.right)) {
            flipColors(current);
        }

        if (isRed(current.left) && isRed(current.left.left)) {
            current = rightRotate(current);
        }

        if (isRed(current.right) && isRed(current.right.right)) {
            current = leftRotate(current);
        }

        return current;
    }

    private void flipColors(Node node) {
        node.color = Color.RED;
        node.left.color = Color.BLACK;
        node.right.color = Color.BLACK;
    }

    private Node rightRotate(Node node) {
        Node newRoot = node.left;
        node.left = newRoot.right;
        newRoot.right = node;

        newRoot.color = node.color;
        node.color = Color.RED;

        return newRoot;
    }

    private Node leftRotate(Node node) {
        Node newRoot = node.right;
        node.right = newRoot.left;
        newRoot.left = node;

        newRoot.color = node.color;
        node.color = Color.RED;

        return newRoot;
    }

    private boolean isRed(Node node) {
        return node != null && node.color == Color.RED;
    }

    public static void main(String[] args) {
        RedBlackTree tree = new RedBlackTree();
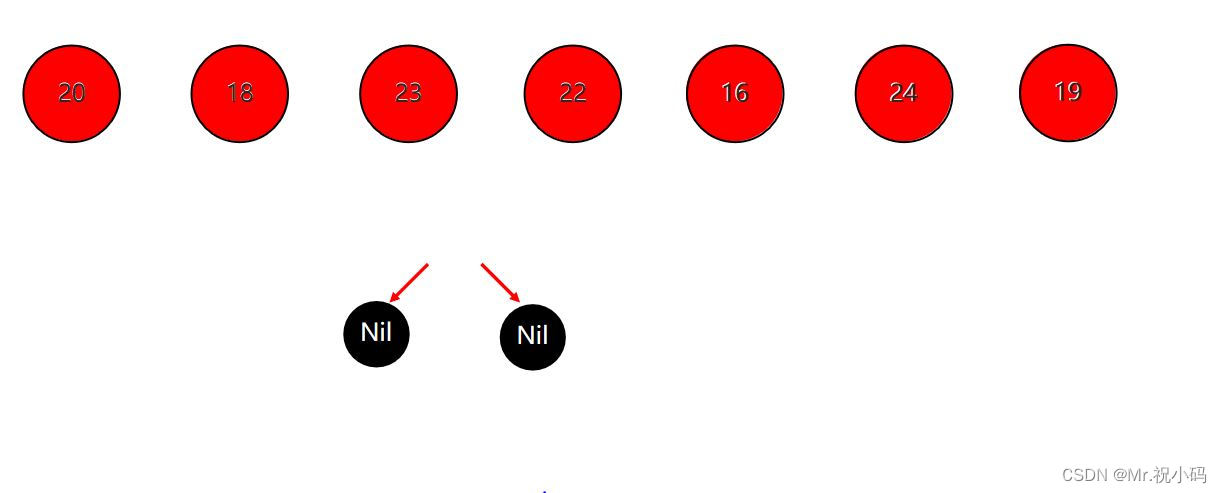
        int[] data = {20, 18, 23, 20, 16, 24, 19};
        for (int value : data) {
            tree.add(value);
        }

        List<Node> redNodes = new ArrayList<>();
        inorderTraversal(tree.root, redNodes);

        System.out.println("Red nodes in the Red-Black tree:");
        for (Node node : redNodes) {
            System.out.print(node.data + " ");
        }
    }

    private static void inorderTraversal(Node node, List<Node> redNodes) {
        if (node != null) {
            inorderTraversal(node.left, redNodes);
            if (node.color == Color.RED) {
                redNodes.add(node);
            }
            inorderTraversal(node.right, redNodes);
        }
    }

    private enum Color {
        RED,
        BLACK
    }

    private static class Node {
        int data;
        Node left;
        Node right;
        Color color;

        public Node(int data) {
            this.data = data;
            this.color = Color.RED;
        }
    }
}

步骤：

           20(B)
             /  \
           18(R) 23(R)
          /   /  \
        16(B) 20(R) 24(B)
               /
             19(R)

红色节点R表示，黑节点B表示

 总结：

红黑树不是高度平衡的，它的平衡是通过"红黑规则"进行实现的 

每一个节点或是红色的，或者是黑色的，根节点必须是黑色

如果一个节点没有子节点或者父节点，则该节点相应的指针属性值为Nil，这些Nil视为叶节点，每个叶节点(Nil)是黑色的；

如果某一个节点是红色，那么它的子节点必须是黑色(不能出现两个红色节点相连的情况) 对每一个节点，从该节点到其所有后代叶节点的简单路径上，均包含相同数目的黑色节点。 

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1667982.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Python模块之Numpy（二）-- 生成各种随机数

Python模块之Numpy（二）-- 生成各种随机数

对于 NumPy&#xff0c;与随机数相关的函数都在 random 模块中&#xff0c;其中包括可以生成服从多种概率分布随机数的函数&#xff0c;示例如下&#xff1a; #生成10个服从0-1均匀分布的随机数 arr1 np.random.random([2,5]) #也生成10个服从0-1均匀分布的随机数 arr2 np.ra…
阅读更多...
TMS320F280049 CLB模块--LUT4 OUTLUT（4）

TMS320F280049 CLB模块--LUT4 OUTLUT（4）

LUT4 示意图如下&#xff1a; OUTLUT 示意图如下&#xff1a; 寄存器 参考文档&#xff1a; TMS320F28004x Real-Time Microcontrollers Technical Reference Manual (Rev. G)
阅读更多...
网络安全之OSI七层模型详解

网络安全之OSI七层模型详解

OSI七层模型分为控制层&#xff08;前三层&#xff09;和数据层&#xff08;后四层&#xff09;。从第七层到一层为&#xff1b; 应用层&#xff08;7&#xff09;接收数据 表示层&#xff08;6&#xff09;将数据翻译为机器语言 会话层&#xff08;5&#xff09;建立虚连接…
阅读更多...
http协议 tomcat如何访问资源 servlet理论介绍

http协议 tomcat如何访问资源 servlet理论介绍

tomcat介绍 bin是启动命令&#xff1b; conf是配置&#xff0c;可以修改端口号&#xff1b; lib是依赖的jar包&#xff1b; logs是日志 webapps是重点&#xff0c;在这里新建我们自己的javaWeb项目 tomcat如何访问资源 tomcat通过统一资源定位符&#xff08;URL&#xff09;来…
阅读更多...
开源软件托管平台gogs操作注意事项

开源软件托管平台gogs操作注意事项

文章目录 一、基本说明二、gogs私有化部署三、设置仓库git链接自动生成参数四、关闭新用户注册入口 私有化部署gogs托管平台&#xff0c;即把gogs安装在我们自己的电脑或者云服务器上。 一、基本说明 系统环境&#xff1a;ubuntu 20.4docker安装 二、gogs私有化部署 前期准…
阅读更多...
权限及权限操作

权限及权限操作

1.命令行解释器 Linux将命令行解释器称为外壳程序shell 命令行解释器的作用就是将用户输入的指令转换为操作系统能够直接执行的指令。同时将操作系统的反馈转换为用户能看懂的反馈&#xff0c;解决了用户和操作系统沟通成本的问题。与此同时&#xff0c;命令行解释器还能够拦…
阅读更多...
环境变量（全）

环境变量（全）

概念 环境变量(environment variables)一般是指在操作系统中用来指定操作系统运行环境的一些参数 如&#xff1a;我们在编写C/C代码的时候&#xff0c;在链接的时候&#xff0c;从来不知道我们的所链接的动态静态库在哪里&#xff0c;但是照样可以链接成功&#xff0c;生成可执…
阅读更多...
设计模式——模板设计模式（Template Method）

设计模式——模板设计模式（Template Method）

模板设计-base 什么是模板&#xff1f; 举个简单的例子&#xff0c;以AABB的格式&#xff0c;写出一个词语&#xff0c;你可能会想到&#xff0c;明明白白&#xff0c;干干净净等&#xff0c; 这个AABB就是一个模板&#xff0c;对模板心中有了一个清晰的概念之后&#xff0c;…
阅读更多...
[hpssupfast@mailfence.com].Elbie勒索病毒如何恢复数据和预防

[hpssupfast@mailfence.com].Elbie勒索病毒如何恢复数据和预防

[hpssupfastmailfence.com].Elbie是一种新型勒索病毒,快速恢复重要数据请添加技术服务号(safe130)。以下是关于elbie勒索病毒的详细信息&#xff1a; 病毒介绍&#xff1a; elbie勒索病毒&#xff0c;也称为PHOBOS勒索软件&#xff0c;它通过加密文件并要求支付赎金以恢复对文…
阅读更多...
spring模块（六）spring监听器（1）ApplicationListener

spring模块（六）spring监听器（1）ApplicationListener

一、介绍 1、简介 当某个事件触发的时候&#xff0c;就会执行的方法块。 当然&#xff0c;springboot很贴心地提供了一个 EventListener 注解来实现监听。 2、源码&#xff1a; package org.springframework.context;import java.util.EventListener; import java.util.fu…
阅读更多...
【数据结构】双向循环链表专题解析

【数据结构】双向循环链表专题解析

实现自己既定的目标&#xff0c;必须能耐得住寂寞单干。&#x1f493;&#x1f493;&#x1f493; 目录 •✨说在前面 &#x1f34b;知识点一&#xff1a;双向链表的结构 • &#x1f330;1."哨兵位"节点 • &#x1f330;2.双向带头循环链表的结构 &#x1f34b;…
阅读更多...
Java - Json字符串转List＜LinkedHashMap＜String,String＞＞

Java - Json字符串转List＜LinkedHashMap＜String,String＞＞

需求&#xff1a;在处理数据时&#xff0c;需要将一个Object类型对象集合转为有序的Map类型集合。 一、问题 1.原代码&#xff1a; 但在使用时出现报错&#xff1a; Incompatible equality constraint: LinkedHashMap<String, String> and LinkedHashMap 不兼容的相等…
阅读更多...
社区送水小程序软件开发

社区送水小程序软件开发

uni-app框架&#xff1a;使用Vue.js开发跨平台应用的前端框架&#xff0c;编写一套代码&#xff0c;可编译到Android、小程序等平台。 框架支持:springboot/Ssm/thinkphp/django/flask/express均支持 前端开发:vue.js 可选语言&#xff1a;pythonjavanode.jsphp均支持 运行软件…
阅读更多...
猫头虎分享已解决Bug || 已解决ERROR: Ruby Gems安装中断 ⚠️ Bug 报告：Gem::RemoteFetcher::FetchError

猫头虎分享已解决Bug || 已解决ERROR: Ruby Gems安装中断 ⚠️ Bug 报告：Gem::RemoteFetcher::FetchError

猫头虎分享已解决Bug || 已解决ERROR: Ruby Gems安装中断 ⚠️ Bug 报告&#xff1a;Gem::RemoteFetcher::FetchError 博主猫头虎的技术世界 &#x1f31f; 欢迎来到猫头虎的博客 — 探索技术的无限可能&#xff01; 专栏链接&#xff1a; &#x1f517; 精选专栏&#xff1a; …
阅读更多...
四川汇昌联信：拼多多运营属于什么行业？

四川汇昌联信：拼多多运营属于什么行业？

拼多多运营属于什么行业?这个问题看似简单&#xff0c;实则涉及到了电商行业的深层次理解。拼多多运营&#xff0c;顾名思义&#xff0c;就是在拼多多这个电商平台上进行商品销售、推广、客户服务等一系列活动。那么&#xff0c;这个行业具体包含哪些内容呢?下面就从四个不同…
阅读更多...
redis深入理解之实战

redis深入理解之实战

1、SpringBoot整合redis 1.1 导入相关依赖 <dependency><groupId>redis.clients</groupId><artifactId>jedis</artifactId> </dependency> <dependency><groupId>org.springframework.boot</groupId><artifactId&g…
阅读更多...
Webstorm免费安装教程

Webstorm免费安装教程

一、介绍 WebStorm 具有智能化的代码编辑功能&#xff0c;如代码补全、重构、代码导航、错误检测等等&#xff0c;这些功能可以帮助开发人员提高编码效率&#xff0c;减少出错的可能性。同时&#xff0c;WebStorm 也集成了各种流行的前端框架和库&#xff0c;如 React、Angula…
阅读更多...
Python3实现三菱PLC串口通讯(附源码和运行图)

Python3实现三菱PLC串口通讯(附源码和运行图)

基于PyQt5通过串口通信控制三菱PLC 废话不多说&#xff0c;直接上源码 """ # -*- coding:utf-8 -*- Project : Mitsubishi File : Main_Run.pyw Author : Administrator Time : 2024/05/09 下午 04:10 Description : PyQt5界面主逻辑 Software:PyCharm "…
阅读更多...
【Linux】轻量级应用服务器如何开放端口 -- 详解

【Linux】轻量级应用服务器如何开放端口 -- 详解

一、测试端口是否开放 1、测试程序 TCP demo 程序&#xff08;可参考&#xff1a;【Linux 网络】网络编程套接字 -- 详解-CSDN博客&#xff09; 2、测试工具 Windows - cmd 窗口 输入命令&#xff1a;telnet [云服务器的公网ip] [port] 二、腾讯云安全组开放端口 1、安全组设…
阅读更多...
简单贪吃蛇的实现

简单贪吃蛇的实现

贪吃蛇的实现是再windows控制台上实现的&#xff0c;需要win32 API的知识 Win32 API-CSDN博客https://blog.csdn.net/bkmoo/article/details/138698452?spm1001.2014.3001.5501 游戏说明 ●地图的构建 ●蛇身的移动&#xff08;使用↑ . ↓ . ← . → 分别控制蛇的移动&am…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023