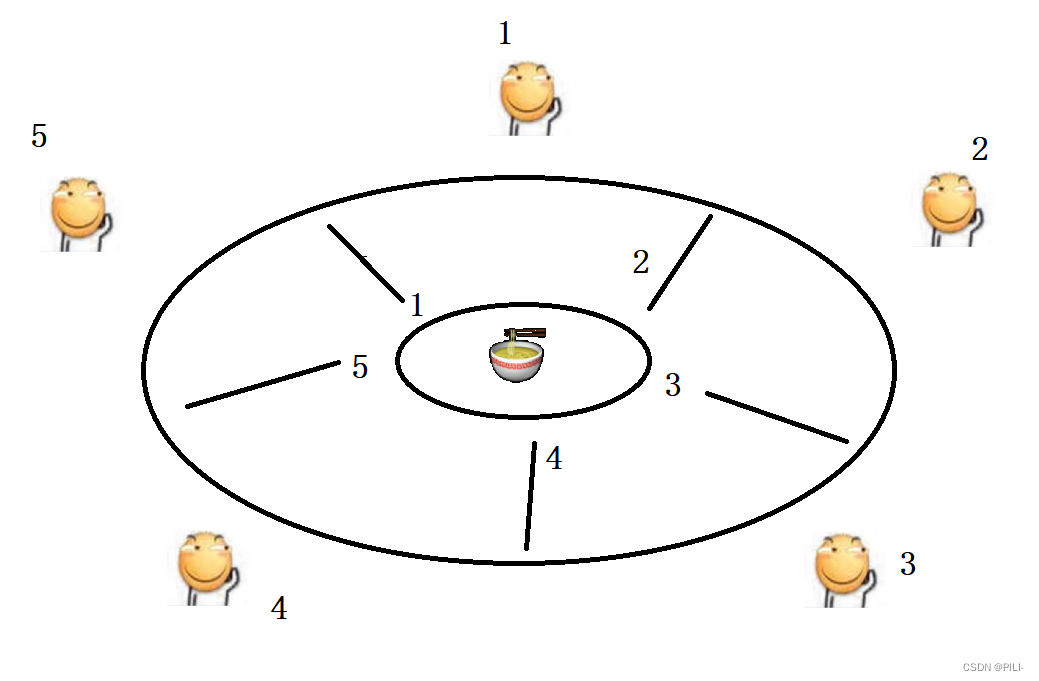
给一棵以节点0为根的树（不一定是二叉树），共有n个节点，0～n-1，
同样的，有长度为n的数组parent, parent[i]表示第 i 个节点的parent, 0的parent是-1.
长度为n的字符串，s(i)表示第i个节点的字母。

返回最长的路径，路径中相邻的节点字母不能相同。

思路：

首先探讨一下什么叫路径。
树的路径可以是(1) 从根节点到叶子节点的路径，(2)任一节点到其他任一节点的路径。
这里是定义(2).

再说下树的直径，定义为树上最远的两个节点之间的距离。

所以本题其实求的是树的直径，长度为路径上的节点数。

case 1:
先讨论一个简单的情形，Example1, 以根节点0为例，
节点0连接的child（即节点2,1）为出发点，能得到最长路径mx1=2（节点2->5），和第二长的路径mx2=2（节点1->3）。

然后从节点0来看，节点2这条路也应该舍弃，因为节点2和节点0的字母相同。所以mx1=2只剩节点1->3这条，所以mx1=2, mx2=0(顺延)。

而节点0将这两个最长路径连接了起来，加上节点0本身，最大路径长度为1+mx1+mx2.

而每个child会返回由它出发的最长路径，所以dfs(node)会返回遍历node所有child所得到的mx1和它自己的和，即1+mx1.

case 2:
节点0-1-2（只有一个分叉的树），s = “aab”
根节点0和1字母都是’a’，不满足条件，是不是要把节点1为根的这个分支砍了，只留节点0，然后最大路径是1？
前面说过了，最大路径是以任一节点出发的，如果从2出发，那最大路径就是2.
所以，以节点1为出发点的路径长度mx1计算出来后，要用它去更新最大路径长度，因为这一段本身也是路径。

另外，本题明确规定了节点的parent关系，可以按有向图处理。

class Solution {
    List<Integer>[] graph;
    int res = 0;

    public int longestPath(int[] parent, String s) {
        int n = parent.length;
        res = 1;
        graph = new ArrayList[n];

        for(int i = 0; i < n; i++) graph[i] = new ArrayList<>();
        for(int i = 1; i < n; i++) graph[parent[i]].add(i); //有向图
        dfs(0, s);
        return res;
    }

    int dfs(int cur, String s) {
        if(graph[cur].size() == 0) return 1;  //叶子节点

        int mx1 = 0;
        int mx2 = 0;

        for(int child : graph[cur]) {
            int len = dfs(child, s);
            res = Math.max(res, len); //case 2

            if(s.charAt(child) == s.charAt(cur)) continue;
            if(len > mx1) {  //case 1
                mx2 = mx1;
                mx1 = len;
            } else {
                mx2 = Math.max(mx2, len);
            }
        }

        res = Math.max(res, 1+mx1+mx2);
        return 1+mx1;
    }
}