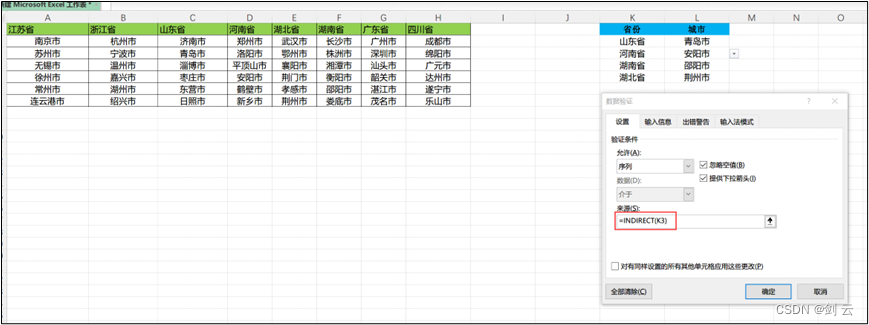
一个物体表面的法向量如何随着物体的坐标变换而改变,取决于变换的类型。使用逆转置矩阵,可以安全地解决该问题,而无须陷入过度复杂的计算中。
法向量变化规律
- 平移变换不会改变法向量,因为平移不会改变物体的方向。
- 旋转变换会改变法向量,因为旋转改变了物体的方向。
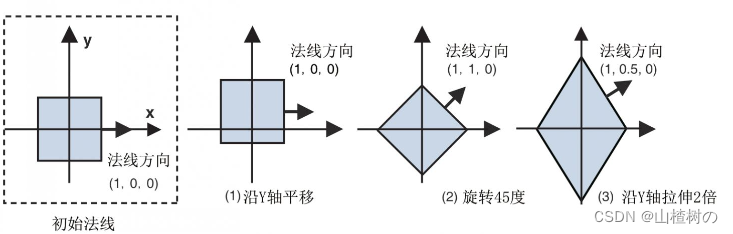
- 缩放变换对法向量的影响较为复杂。如上图,最右侧的图显示了立方体先旋转了45度,再在y轴上拉伸至原来的2倍的情况。此时法向量改变了,因为表面的朝向改变了。但是,如果缩放比例在所有的轴上都一致的话,那么法向量就不会变化。
模型矩阵的逆转值矩阵可以用来变换法向量。实际上,在某些特殊情况下,可以通过模型矩阵来确定物体变换后的法向量。比如说,当物体在旋转时,可以用旋转矩阵直接乘以法向量,就能获得旋转后的法向量。总之,计算变换后的物体表面的法向量方向时,是求诸于模型矩阵自身,还是模型矩阵的逆转值矩阵,取决于模型矩阵中已经包含的变换类型(平移、旋转或缩放)。
直接通过模型矩阵自身求变换后的法向量。如果模型矩阵中已经包含了平移变换,法向量就会被当作顶点坐标平移,从而导致法向量与原有的表面朝向不一致。比如说,一个法向量是(1,0,0),沿Y轴平移2.0个单位后,就变成了(1,2,0)。事实上,如果你从4×4的模型矩阵的左上角抽出3×3的子矩阵,然后乘以法向量,就可以避免该问题。如下所示,4*4的模型矩阵:

由于3×3的子矩阵实际上包含了旋转矩阵和缩放矩阵的信息,我们来逐一考虑。
- 如果只进行旋转操作:
你可以使用模型矩阵的3×3子矩阵对法向量进行变换。如果在变换前法向量已经归一化了,那么变换后的法向量无须再归一化处理。
- 如果只进行缩放操作(且缩放因子相同):
你可以使用模型矩阵的3×3子矩阵对法向量进行变换。但是,变换后的法向量需要再次归一化处理。
在这种情况下,当你只进行缩放操作且缩放因子相同时,这意味着X轴、Y轴和Z轴的缩放因子是一致的。比如,你希望以一致的缩放因子2.0进行缩放,那么就需要将法向量 3*3 子矩阵 变换后归一化,这时,即使物体的尺寸发生了变化,但是其形状并未改变。
- 如果进行了缩放操作(但缩放因子不同):
必须使用模型矩阵的逆转值矩阵对法向量进行变换。变换后的法向量必须再次归一化处理。原因如下:
如下图使一个矩形物体(左图)沿Y轴拉伸2.0倍,拉伸后的形状如右图所示。这里,为了获得变换后的法向量,我们试图使用模型矩阵乘以原先的法向量(1,1,0)。但是,得到的结果是(1,2,0),并不垂直于拉伸后的物体表面了。

推导
令模型矩阵为M,令初始的法向量为n,令变换矩阵为M',也就是用来正确变换法向量n的矩阵,令垂直于n的向量为s,令变换后的法向量为n',令垂直于n'的向量为s'
有等式一、二:
n' = M' * n
s' = M * s
n和s,以及 n'和 s'的关系 ,如下:
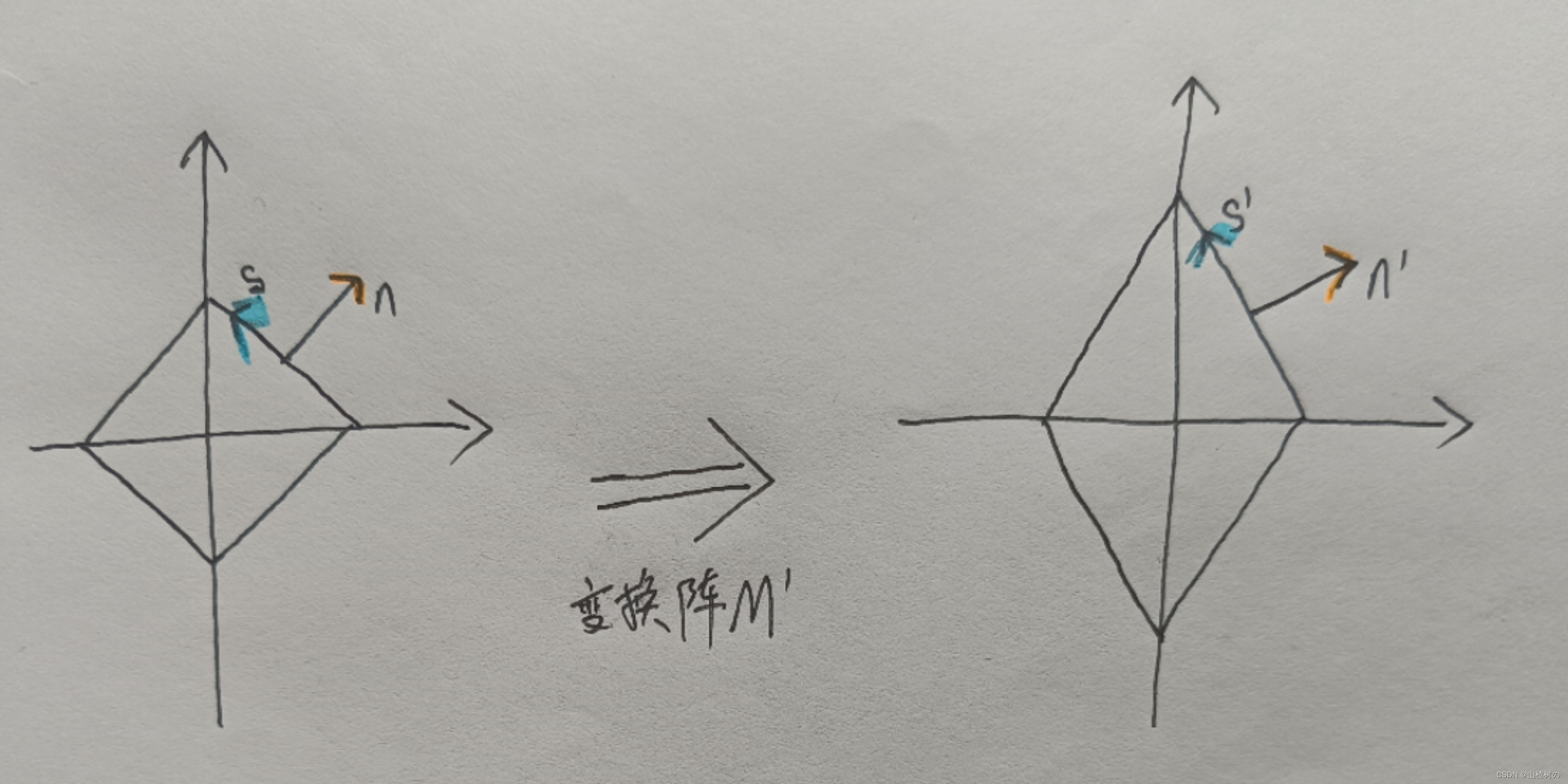
现在,我们就来计算M',使得n'和s'的相对角度保持垂直。我们知道两个垂直矢量的点积是0,点乘操作使用点运算符“ · ”表示,所以有:
n'· s'= 0
将等式一、二代入并重写上式

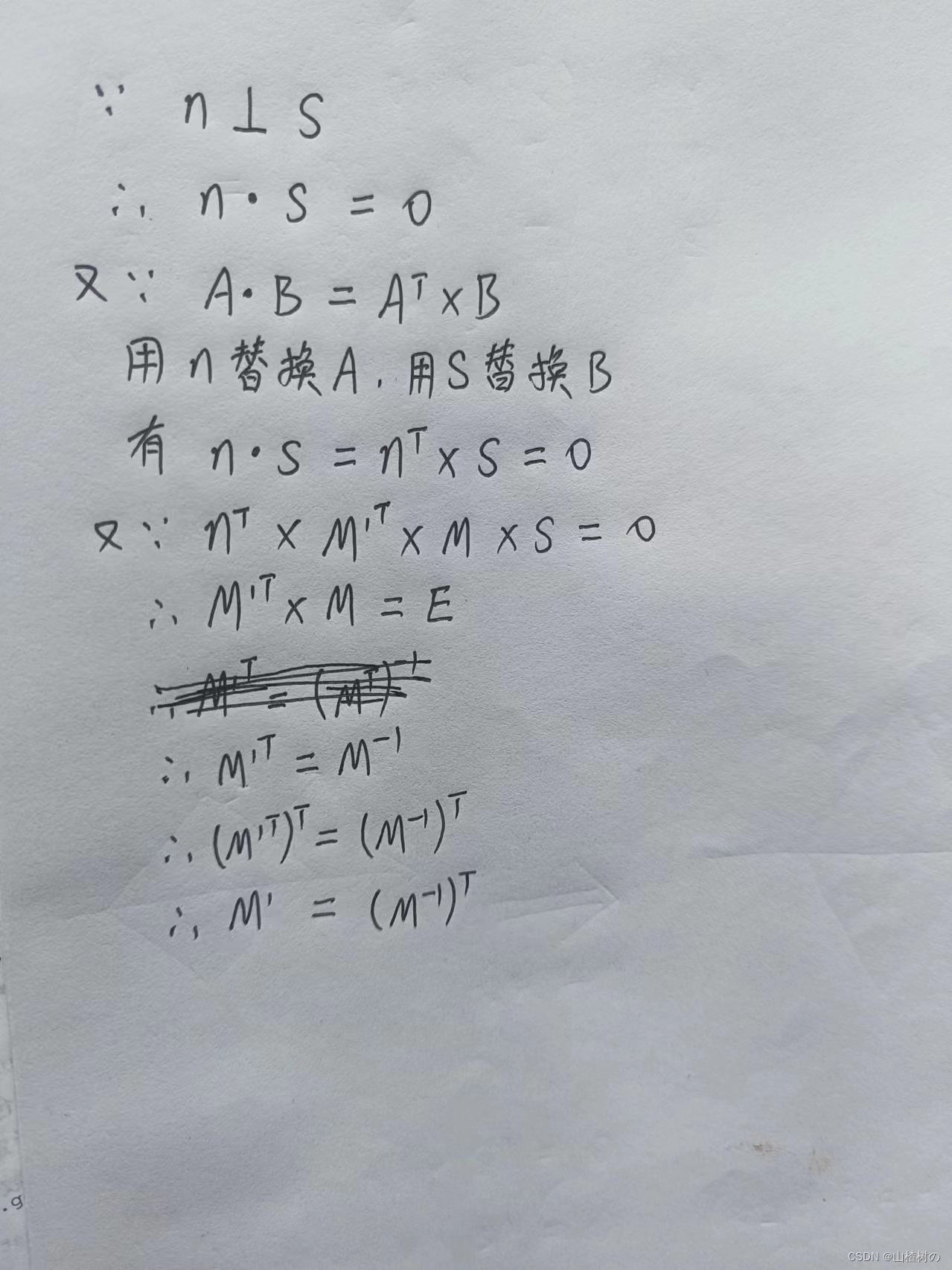
从上图中可以看出,M'就是通过转置M的逆矩阵得到的,或者说,M'就是M的逆转置矩阵。因为M已经可能包含了上面列举过的三种变换情况,所以计算M的逆转置矩阵并乘以法向量,就可以获得正确的结果,因此,这才是对法向量进行变换的最佳方法
另,计算逆转置矩阵可能会比较耗时,如果你非常确定物体的变换只包含上述(1)(2)的情形,也可以简单地使用上述 模型矩阵的3×3子矩阵 来对处理法向量。