有一位国王拥有5座金矿,每座金矿的黄金储量不同,需要参与挖掘的工人人数也不同。
例如,有的金矿储量是5ookg黄金,需要5个工人来挖掘;有的金矿储量是2ookg黄金,需要3个工人来挖掘...... 如果参与挖矿的工人的总数是10。每座金矿要么全挖,要么不挖,不能派出一半人挖取一半的金矿。要求用程序要想得到尽可能多的黄金,应该选择挖取哪几座金矿?
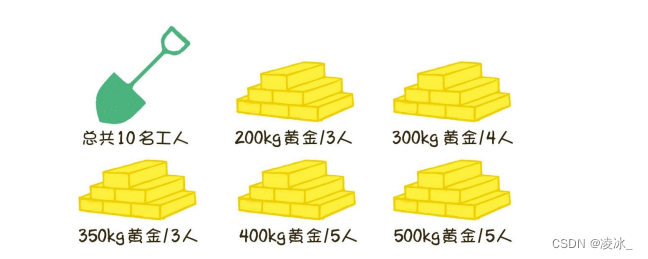
金矿按照性价比从高到低进行排序,排名结果如下:
第1名,350kg黄金/3人的金矿,人均产量约为116.6kg黄金。
第2名,500kg黄金/5人的金矿,人均产量为100kg黄金。
第3名,400kg黄金/5人的金矿,人均产量为80kg黄金。
第4名,300kg黄金/4人的金矿,人均产量为75kg黄金。
第5名,200kg黄金/3人的金矿,人均产量约为66.6kg黄金。
由于工人数量是10人,优先挖掘性价比排名为第1名和第2名的金矿之后,工人还剩下2人,不够再挖掘其他金矿了。
得出的最佳金矿收益是350+500即850kg黄金。
解决思路是使用贪心算法。这种思路在局部情况下是最优解,但是在整体上却未必是最优的。
如果我放弃性价比最高的350kg黄金/3人的金矿,选择500kg黄 金/5人和400kg黄金/5人的金矿,加起来收益是900kg黄金,是不是大于你得到的850kg黄金?
动态规划,就是把复杂的问题简化成规模较小的子问题,再从简单的子问题自底向上一步一步递推,最终得到复杂问题的最优解。
10个工人在前4个金矿的收益,和7个工人在前4个金矿的收益+最后一个金矿的收益谁大谁小了。

首先针对10个工人4个金矿这个子结构,第4个金矿(300kg黄金/4人)可以选择挖与不挖。根据第4个金矿的选择,问题又简化成了两种更小的子结构:
1、10个工人在前3个金矿中做出最优选择。
2、(10-4=6)6个工人在前3个金矿中做出最优选择。
相应地,对于7个工人4个金矿这个子结构,第4个金矿同样可以选择挖与不挖。根据第4个金矿的选择,问题也简化成了两种更小的子结构:
1、7个工人在前3个金矿中做出最优选择。
2、(7-4=3)3个工人在前3个金矿中做出最优选择。
就这样,问题一分为二,二分为四,一直把问题简化成在0个金矿或0个工人时的最优选择,这个收益结果显然是0,也就是问题的边界。
这就是动态规划的要点:确定全局最优解和最优子结构之间的关系,以及问题的边界。
这个关系用数学公式来表达,叫作状态转移方程式。
金矿数量设为n,工人数量设为w,金矿的含金量设为数组g[],金矿所需开采人数设为数组p[],设F (n,w)为n个金矿、w个工人时的最优收益函数,那么状态转移方程式如下:
F(n,w) =0 (n=0或w=0) 问题边界,金矿数为0或工人数为0的情况。
F(n,w)=F(n-1,w)(n≥1,w<p[n-1]) 当所剩工人不够挖掘当前金矿时,只有一种最优子结构。
F(n,w)= max(F(n-1,w),F(n-1,w-p[n-1])+g[n-1])(n≥1,wzp[n-1]) 在常规情况下,具有两种最优子结构(挖当前金矿或不挖当前金矿)。

在上图中,标为橘色的方法调用是重复的。可以看到F (2,7) 、F(1,7)、F (1,2)这几个入参相同的方法都被调用了两次。
当金矿数量为5时,重复调用的问题还不太明显。金矿数量越多,递归层次越深,重复调用也就越多,这些无谓的调用必然会降低程序的性能。
动态规划的另一个核心要点:自底向上求解。
此时,最后1行最后1个格子所填的900就是最终要求的结果,即5个金矿、10个工人的最优收益是9ookg黄金。
使用二维数组来代表表格
def get_best_gold(worker,person=[],gold=[]):
'''
:param worker: 工人数量
:param person: 金矿开采人数
:param gold: 金矿存储量
:return: 最优收益
'''
#初始化表格0
r_table=[[0 for i in range(worker+1)] for j in range(len(gold)+1)]
double_for(r_table)
print('&'*50)
#填充表格数据
for i in range(1,len(gold)+1):
for j in range(1,worker+1):
if j<person[i-1]:
r_table[i][j]=r_table[i-1][j]
else:
r_table[i][j] =max(r_table[i - 1][j],r_table[i - 1][j-person[i-1]]+gold[i-1])
double_for(r_table)
#返回最后一个格子的数据
return r_table[len(gold)][worker]
def double_for(ll):
for row in ll:
print(row)
if __name__ == '__main__':
#采矿人数
person=[5,5,3,4,3]
#采矿黄金量
gold=[400,500,200,300,350]
print(get_best_gold(10, person, gold))

程序利用双循环来填充一个二维数组,所以时间复杂度和空间复杂度都是O ( nw) ,比递归的性能好多啦!
def get_best_gold2(worker,person=[],gold=[]):
'''
优化
:param worker: 工人数量
:param person: 金矿开采人数
:param gold: 金矿存储量
:return: 最优收益
'''
#初始化表格0
results=[0]*(worker+1)
print(results)
#填充一维数据
for i in range(1,len(gold)+1):
for j in range(worker,0,-1):
if j>=person[i-1]:
results[j] =max(results[j],results[j-person[i-1]]+gold[i-1])
print(results)
#返回最后一个格子的数据
return results[worker]
if __name__ == '__main__':
#采矿人数
person=[5,5,3,4,3]
#采矿黄金量
gold=[400,500,200,300,350]
print(get_best_gold2(10, person, gold))

空间复杂度降低到了O (n)。