参考文献:
[1]徐岩,张荟,孙易洲.基于变异粒子群算法的主动配电网故障恢复策略[J].电力自动化设备,2021,41(12):45-53.DOI:10.16081/j.epae.202108030.
1.基本原理
为提高主动配电网故障恢复的快速性和可靠性,提出一种基于变异粒子群算法的恢复策略。光储系统与负荷特性模型的构建是研究策略的基础,利用光储模型保证负荷可靠恢复,在构建负荷特性模型时考虑负荷时变性、需求时变性及负荷可控性的特点。在建立的光储系统与负荷特性模型基础上研究故障恢复策略,首先对配电网进行动态孤岛划分,利用光储系统对孤岛内负荷进行可靠恢复,保证用户侧需求度高的负荷优先恢复,然后以总失电负荷最少、网损最小及开关动作次数最少为综合目标函数,运用变异粒子群算法得到孤岛与主网配合的配电网综合恢复策略,提高了主动配电网可靠性。最后,采用IEEE 33节点系统进行算例分析,结果验证了模型与恢复策略的优越性。
1.1 动态孤岛划分策略
在故障恢复过程中为充分利用 DG 出力,利用孤岛划分对配电网中的重要负荷进行恢复。
1.1.1孤岛划分的原则
在研究配电网孤岛划分方案时,应考虑以下原则:
1)确保方案在孤岛运行时能够安全、稳定,且具备并入主网运行的能力;
2)在保证孤岛内的负荷与损耗之和小于分布式光伏出力容量的前提下,孤岛内应包含尽可能多的负荷,这样既能充分发挥分布式光伏的供电能力,又不会造成过负荷的情况;
3)在进行孤岛划分时,应优先恢复FRload,t中的负荷。
1.1.2动态孤岛划分数学模型
当含有分布式光储系统的配电网发生故障时,根据光伏在故障时段的实际出力,对配电网进行孤岛划分,利用孤岛对重要负荷进行供电恢复,以提高供电可靠性。
1)目标函数
利用光伏系统在故障时刻的实际出力作为孤岛的供电量,考虑在孤岛划分过程中,首先恢复 FRload,t中的负荷,切除最少的负荷,尽可能多地恢复其他负荷。因此,t时刻孤岛划分的目标函数为:
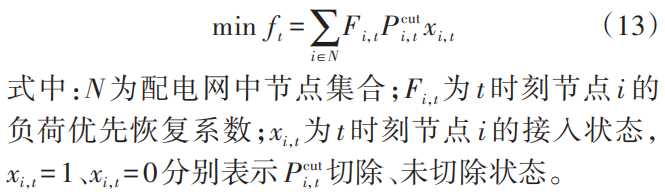
2)约束条件
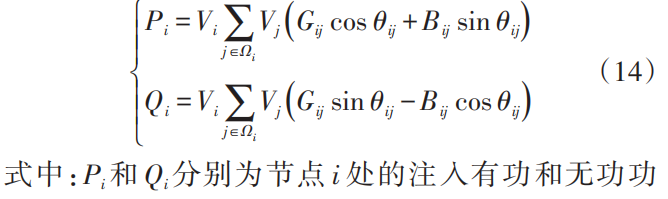

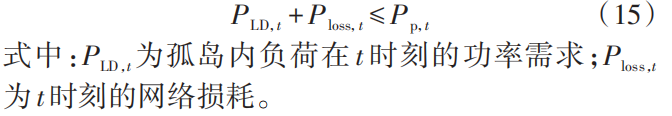


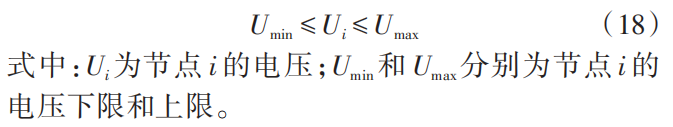
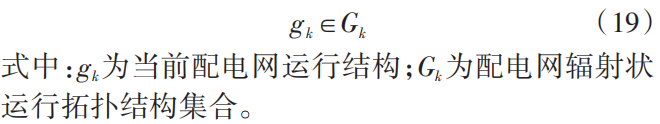
1.1.3拓扑搜索方法
利用广度优先搜索BFS(Breadth First Search)与深度优先搜索DFS(Depth-First Search)法在孤岛划分过程中对配电网拓扑进行搜索。BFS法是从图中的根节点开始搜索与之相连的节点,并对该层节点进行编号,再以该层节点作为顶点继续搜索下一层的子节点,按照此操作逐层搜索,直至搜索完所有节点。DFS 法是从图中的根节点开始搜索,如果发现有以此为起点的边未被搜索到,则沿此边继续搜索,当某一节点所有的边都被搜索完毕后,搜索回溯到发现该节点的边的起始点,直至搜索完根节点可达的所有节点。
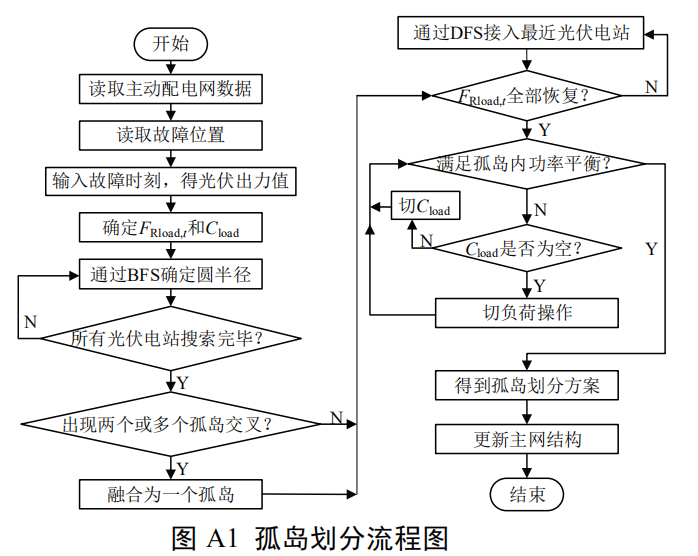
1.1.4 孤岛划分流程
在故障时刻利用分布式光储系统对孤岛内的负荷进行恢复,孤岛划分流程如附录 A 图 A1 所示。
1.2故障恢复策略
1.1中利用光储系统孤岛运行对配电网中的FRload,t进行恢复,本节在孤岛划分的基础上,利用DG与主网的协调控制对配电网进行恢复,对孤岛内开关重新编码并令其参与主网的恢复过程,采用变异粒子群算法MPSO(Mutation Particle Swarm Optimization algorithm)在保证原孤岛内恢复的负荷不断电的同时进行最优故障恢复方案的设计。
1.2.1目标函数
在故障恢复问题的研究中,设计的目标函数包括总失电负荷最少、网损最小、开关动作次数最少,如式(24)所示。

约束条件同式(14)—(19)。
1.2.2故障恢复策略
故障恢复策略的流程如附录A图A2所示:

2.求解方法
2.1 BPSO
粒子群算法已广泛应用于配电网故障恢复策略的研究中,该算法具有操作简单、收敛速度快、易于实现等优点。由于配电网中的开关操作只存在开、合2种状态,因此对BPSO进行改进,利用离散BPSO解决配电网故障恢复问题。
每个粒子代表一组开关的状态,若开关闭合,则粒子中对应的位取值为 1,若断开则取值为 0。在离散 BPSO中,每个二进制位的速度更新公式为:

由于离散 BPSO 没有原始粒子群算法的粒子位置更新公式,因此利用位变量取 1 的概率表示粒子的速度。利用 sigmoid 函数将速度 vid 映射到区间[0,1]内,如式(21)所示,粒子通过式(22)改变位置。
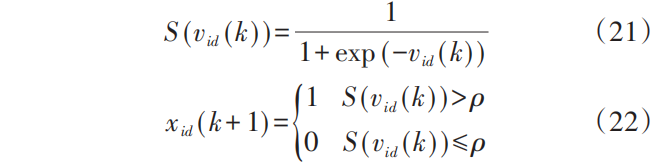

2.2 MPSO
由于离散BPSO自身存在易陷入局部最优、收敛早熟等问题,引入线性微分递减惯性权重 LDIW(Linear Decreasing Inertia Weight)和非对称线性变换学习因子以改进算法的收敛速度与收敛精度。
GA 中的交叉与变异操作可以提高算法的全局搜索能力,因此将离散 BPSO 与GA 进行优势互补,将交叉与变异操作应用到离散BPSO中,从而得到MPSO。
1)引入线性微分递减惯性权重。
惯性权重w影响算法的搜索能力,当 w 取值较大时算法的全局搜索能力较强,当 w 取值较小时算法的局部搜索能力较强,因此为了使算法在早期具有较强的全局搜索能力,在后期又可以进行精确局部搜索,引入线性微分递减惯性权重如式(23)所示。

2)引入非对称线性变换学习因子。
学习因子影响算法的搜索能力和收敛速度,为了使算法在迭代前期的全局搜索能力较强、后期的收敛速度快,利用非对称线性变换对学习因子进行改进,更新公式为:
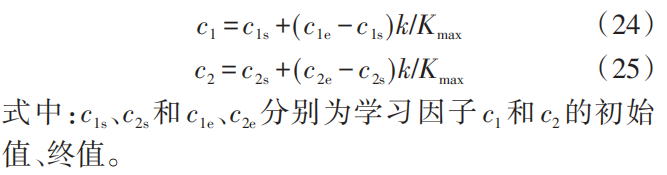
3)引入 GA 的交叉、变异操作。
由于离散BPSO收敛速度较快,存在易于陷入局部最优的问题 在种群更新中粒子自身信息占优势,而 GA 中的交叉、变异操作可以有效解决该问题,因此将其引入离散BPSO中。
交叉操作是通过某种方式将相互交叉的 2个染色中的部分基因进行交换,从而得到2个新个体,交叉操作可以有效提高算法的全局搜索能力,将该操作引入离散 BPSO 中可以改善其易于陷入局部最优的问题。交叉操作首先是种群中的粒子进行随机配对,按照选定的交叉概率pc进行交叉,在迭代过程中按照pc生成杂交粒子池如式(26)所示。

新的粒子xi和xj的位置、速度更新公式分别为:

变异操作可以产生新的个体,提高算法的局部搜索能力,同时能够保持种群的多样性,防止收敛早熟现象的发生。将高斯变异引入离散 BPSO 中,在迭代过程中以变异概率 pm生成变异粒子池,如式(29)所示。

3.编程思路分析
根据对文献内容的解读,可以设计下面的编程思路:
步骤1:输入所需数据
这一步比较简单。算例分析用到的大部分数据可以从原文中找到,IEEE33节点系统直接使用matpower工具箱中的数据即可,其他没有给出的数据可以自己假设一下。
步骤2:MPSO算法的实现
实现基本的BPSO算法,并采用文中的改进策略对其进行改进,得到MPSO算法,使用测试函数测试算法的有效性。
步骤3:动态孤岛划分算法的实现
采用原文献中所提孤岛划分方法,得到配电网孤岛划分策略。
步骤4:将MPSO算法用于配电网故障恢复问题
使用MPSO算法求解配电网故障恢复问题时,决策变量应设置为配电网的支路开断状态,由于文献中采用了IEEE33节点配电网,其支路数为37,因此决策变量的维度也是37,且均为0-1变量。
此外,原文献中并没有对粒子群的初始化和更新做出特殊的设计,单纯的随机处理,将产生大量不可行解,因此代码中将使用之前博客中所提到的方法对粒子群进行初始化和更新(基于改进二进制粒子群算法的配电网重构(matlab实现)_粒子群算法网络重构-CSDN博客)。
步骤5:输出运行结果
参考文中的图表的格式,输出结果即可。
4.Matlab代码
%% BPSO算法
clc
clear
close all
%% 设置种群参数
sizepop = 200; % 初始种群个数
dim = 100; % 空间维数
ger = 500; % 最大迭代次数
v_max = 3; % 速度上限
v_min = -3; % 速度下限
w = 0.9; % 惯性权重
c_1 = 1.5; % 自我学习因子
c_2 = 1.5; % 群体学习因子
%% 种群初始化
pop = randi([0, 1] , sizepop, dim); % 初始化种群
pop_v = v_min + rand(sizepop,dim).*(v_max-v_min); % 初始化种群速度
pop_zbest = pop(1,:); % 初始化群体最优位置
pop_gbest = pop; % 初始化个体最优位置
fitness = zeros(1,sizepop); % 所有个体的适应度
fitness_zbest = inf; % 初始化群体最优适应度
fitness_gbest = inf*ones(1,sizepop); % 初始化个体最优适应度
%% 初始的适应度
for k = 1:sizepop
% 计算适应度值
fitness(k) = fitnessfun(pop(k,:));
if fitness(k) < fitness_zbest
fitness_zbest = fitness(k);
pop_zbest = pop(k,:);
end
end
history_pso = zeros(1,ger); % 粒子群历史最优适应度值
%% 迭代求最优解
iter = 1;
while iter <= ger
for k = 1:sizepop
% 更新速度并对速度进行边界处理
pop_v(k,:)= w * pop_v(k,:) + c_1*rand*(pop_gbest(k,:) - pop(k,:)) + c_2*rand*(pop_zbest - pop(k,:));
for kk = 1:dim
if pop_v(k,kk) > v_max
pop_v(k,kk) = v_max;
end
if pop_v(k,kk) < v_min
pop_v(k,kk) = v_min;
end
end
% 更新位置
S = sigmoid(pop_v(k,:));
R = rand(1,dim);
for kk = 1:dim
if S(kk) > R(kk)
pop(k, kk) = 1;
else
pop(k, kk) = 0;
end
end
% 更新适应度值
fitness(k) = fitnessfun(pop(k,:));
if fitness(k) < fitness_zbest
fitness_zbest = fitness(k);
pop_zbest = pop(k,:);
end
if fitness(k) < fitness_gbest(k)
fitness_gbest(k) = fitness(k);
pop_gbest(k,:) = pop(k,:);
end
end
history_pso(iter) = fitness_zbest;
disp(['PSO第',num2str(iter),'次迭代最优适应度=',num2str(fitness_zbest)])
iter = iter+1;
end
% time0 = toc;
% disp(['运行时间为:',num2str(time0) , '秒'])
disp(['最优解:x=',num2str(pop_zbest)])
disp(['最优函数值=',num2str(fitness_zbest)])
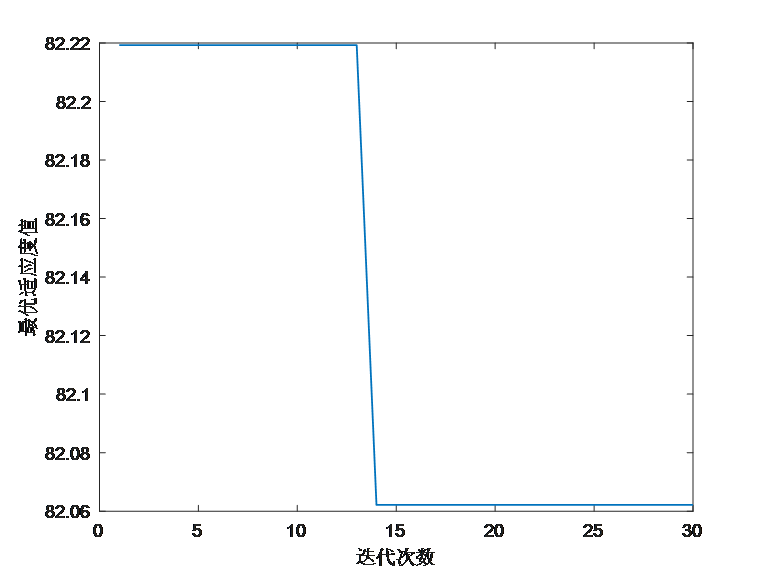
plot(history_pso,'linewidth',1)
ylabel('最优适应度值')
xlabel('迭代次数')
function fitness = fitnessfun(pop)
fitness = sum(pop.^2);
end完整matlab代码获取
以上仅为基本BPSO算法求解测试函数的matlab代码,完整论文复现的matlab代码可以从这个链接获取:
(文章复现)基于变异粒子群算法的主动配电网故障恢复策略matlab代码资源-CSDN文库
压缩包中共包含13个m文件,具体说明分别如下:
4.1.BFS.m
为广度优先搜索算法BFS(Breadth-First Search)的子函数。
4.2.BPSO.m
基本BPSO算法求解测试函数sphere最小值的程序。
4.3.creat_pso.m
粒子群算法求解故障恢复策略初始化的子函数。
4.4.DFS.m
深度优先搜索算法的子函数。
4.5.dfs_shortest_paths.m
采用DFS求解最短路径的子函数。
4.6.fitnessfun.m
配电网故障恢复策略目标函数的计算子函数。
4.7.IEEE33.m
IEEE 33节点配电网的数据文件。
4.8.main_island.m
孤岛划分的程序
4.9.main.m
程序的主函数,使用时只需要运行该程序即可得到所有的结果。
4.10.main_service_recovery.m
基于MPSO求解主动配电网故障恢复策略的程序
4.11.MPSO.m
MPSO算法求解测试函数sphere最小值的程序。
4.12.parameters.m
相关的参数。
4.13.sigmoid.m
Sigmoid函数的计算子函数。
5.运行结果
5.1 场景1的孤岛划分结果


5.2 场景2的孤岛划分结果

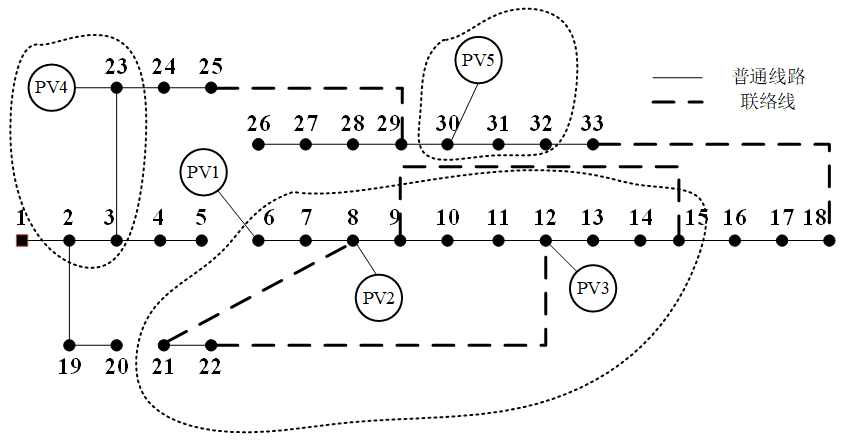
5.3 场景1的故障恢复策略


5.4 场景2的故障恢复策略