一、引言
论文: Swin Transformer: Hierarchical Vision Transformer using Shifted Windows
作者: Microsoft Research Asia
代码: Swin Transformer
特点: 提出滑动窗口自注意力 (Shifted Window based Self-Attention) 解决Vision Transformer输入高分辨率图像注意力模块计算复杂度高的问题。
二、框架
Swin Transformer的整体框架图如下:

可见,Swin Transformer主要包括Patch Partition+Linear Embedding、Swin Transformer Block、Patch Merging几个组件。每经历一个Stage特征图都会缩小2倍、通道数放大2倍,这与ResNet网络的特征尺度变化过程很类似。
Swin Transformer Block的最小单位为上图右侧两个连续的Block,两个Block的差别仅在于注意力模块是窗口多头自注意力 (W-MSA) 还是滑动窗口多头自注意力 (SW-MSA)。所以每个Stage中包含的Block数量都是2的整数倍。
2.1 Patch Partition+Linear Embedding
Patch Partition是要将图像拆分成多个 4 ∗ 4 ∗ 3 4*4*3 4∗4∗3大小的Patch(4*4是每个Patch包含的像素点数,3是原始图像通道数),如下图所示:

之后将每个Patch按行展平,于是每个Patch形成一个 1 ∗ 1 ∗ 48 1*1*48 1∗1∗48的像素点。 48 = 4 ∗ 4 ∗ 3 48=4*4*3 48=4∗4∗3,原本一个像素点通道数为3,一个Patch有 4 ∗ 4 4*4 4∗4个像素点,所以展平后一个Patch变成一个通道数为48的像素点。所有Patch展平后按原位置拼接则形成 H 4 ∗ W 4 ∗ 48 \frac{H}{4}*\frac{W}{4}*48 4H∗4W∗48的特征图。
通过Linear Embedding(例如核为 1 ∗ 1 1*1 1∗1的2D卷积)将通道数从48映射到 C C C(原文中 C = 96 C=96 C=96)。最后通过LayerNorm将所有通道数为 C C C的像素点归一化。
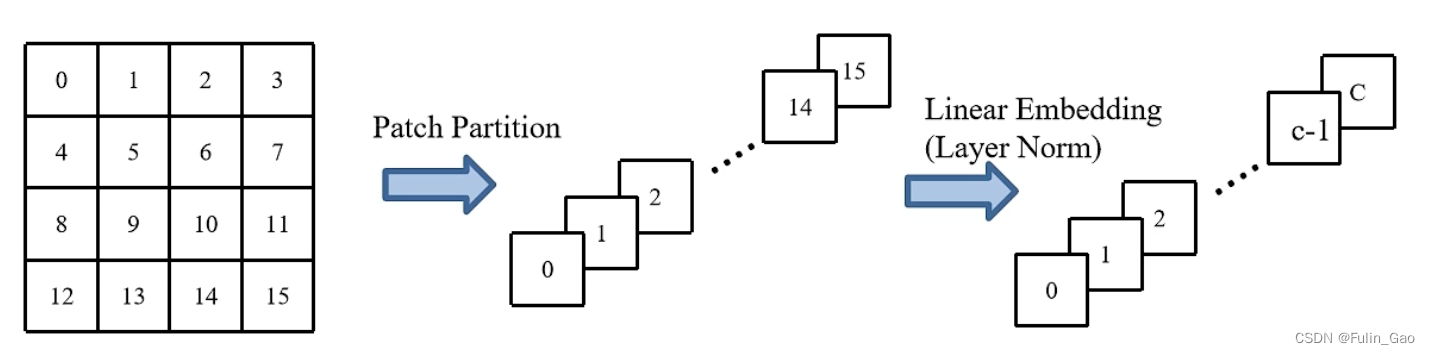
上图为一个Patch上16个像素点的Patch Partition+Linear Embedding过程(图中一个小方格代表一个有3个通道的像素点, c = C 3 c=\frac{C}{3} c=3C)。
事实上,Patch Partition+Linear Embedding就是要将图像尺寸从 H ∗ W ∗ 3 H*W*3 H∗W∗3转换为 H 4 ∗ W 4 ∗ C \frac{H}{4}*\frac{W}{4}*C 4H∗4W∗C。 与Vision Transformer取Patch时采取的策略一致,Swin Transformer并没有分两步完成该操作,而是通过一个卷积核大小为 4 ∗ 4 4*4 4∗4、步长为4、输出通道数为96的2D卷积层进行特征提取,再通过LayerNorm对所有token进行归一化(一个token对应 H 4 ∗ W 4 ∗ C \frac{H}{4}*\frac{W}{4}*C 4H∗4W∗C的特征图中的一个像素点)。
2.2 Swin Transformer Block
下图为Vision Transformer(左)和Swin Transformer(右)中Block的结构图:
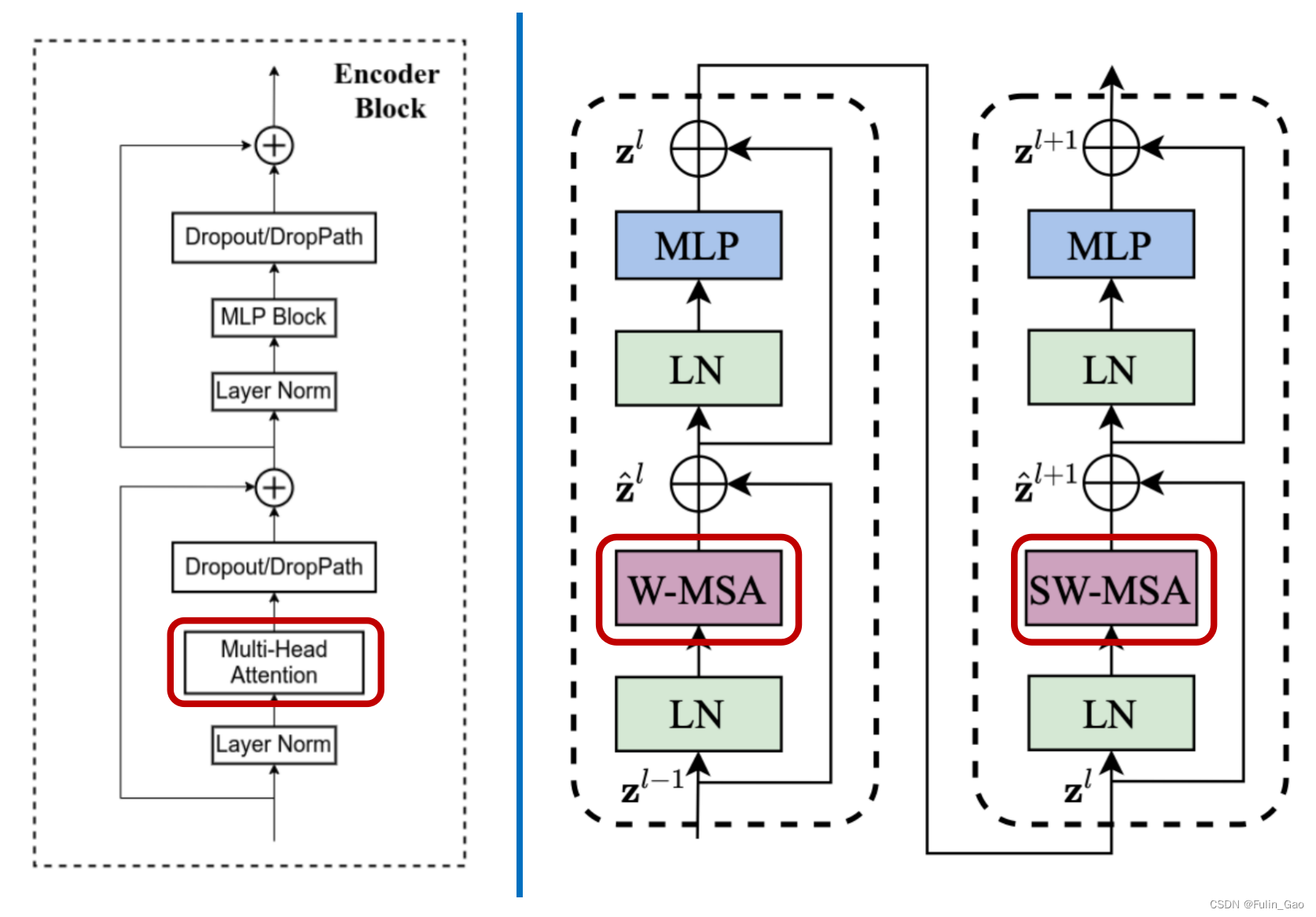
其中,Swin Transformer中也有DropPath但是没有画出来,并且他们的MLP模块均为如下结构:
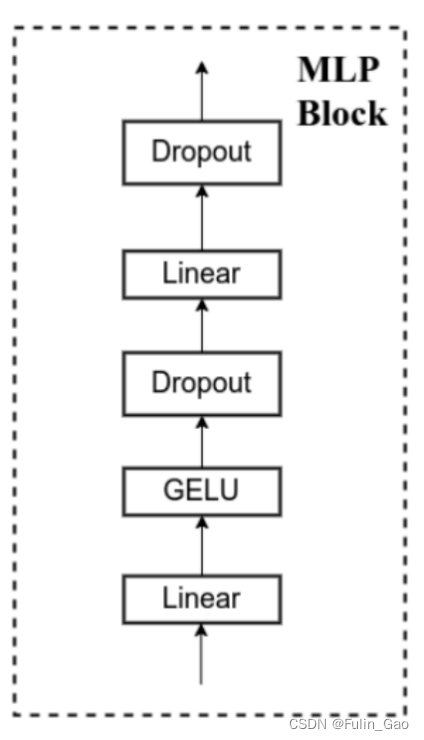
可见,两者结构基本一致,主要区别如下:
(1) Vision Transformer的每一个Block都一样,而Swin Transformer中两个不同的Block是一个基本单位,两个Block顺序连接,不会单独出现。
(2) Vision Transformer使用多头自注意力,而Swin Transformer中两个Block注意力模块不同,前一个使用窗口多头自注意力,后一个使用滑动窗口多头自注意力。
(3) Vision Transformer使用绝对位置编码,而Swin Transformer使用相对位置编码。
所以我们下面主要介绍窗口多头自注意力和滑动窗口多头自注意力,其余部分请参考我关于Vision Transformer的博客。
2.2.1 窗口多头自注意力
引入窗口多头自注意力 (W-MSA) 是为了减少计算复杂度。
如下为多头自注意力 (MSA) 与窗口多头自注意力的窗口划分方法:

多头自注意力不对特征图进行划分,左图中共16个像素点(也叫token),每个像素点作为query时都要与所有像素点进行自注意力计算。而窗口多头自注意力会先将特征图拆分为一个个窗口(右图中窗口高宽为 2 ∗ 2 2*2 2∗2),然后在每个窗口内部单独进行自注意力计算。
两者的计算复杂度如下:

其中, h h h为特征图高度, w w w为特征图宽度, C C C为特征图通道数, M M M为每个窗口的大小;自注意力的计算是以特征图或窗口上的token为单位的,所以未被拆分的特征图中应包含 h w hw hw个长度为 C C C的token。该计算复杂度不包括除以 d k \sqrt{d_k} dk和SoftMax产生的计算量。
在讲解两者计算复杂度推导过程前,我们需要明确两个矩阵相乘所产生的计算量,如果 A A A矩阵高宽为 a ∗ b a*b a∗b, B B B矩阵高宽为 b ∗ c b*c b∗c,则 A ⋅ B A\cdot B A⋅B的计算量为 a ∗ b ∗ c a*b*c a∗b∗c。
下图实线部分为单头自注意力的计算过程:

其中,黑色字体为当前矩阵含义,红色字体为当前矩阵高宽,绿色和橙色字体为当前运算复杂度。多头自注意力在通道上对token的拆分不会影响计算复杂度,所以除最后将 A ⋅ V A\cdot V A⋅V通过 W o W_o Wo映射为输出时产生的计算复杂度(上图右侧虚线部分),其余与单头自注意力计算复杂度相同。于是,我们可以得到多头自注意力的计算复杂度为 4 h w C 2 + 2 ( h w ) 2 C 4hwC^2+2(hw)^2C 4hwC2+2(hw)2C。
对于窗口多头自注意力,特征图大小为 h ∗ w h*w h∗w,窗口大小为 M ∗ M M*M M∗M时,则从特征图上可拆分出 h M ∗ w M \frac{h}{M}*\frac{w}{M} Mh∗Mw个窗口。每个窗口单独执行多头自注意力产生计算复杂度为 4 M 2 C 2 + 2 M 4 C 4M^2C^2+2M^4C 4M2C2+2M4C。则 h M ∗ w M \frac{h}{M}*\frac{w}{M} Mh∗Mw个窗口的总计算复杂度为 4 h w C 2 + 2 M 2 h w C = h M ∗ w M ∗ ( 4 M 2 C 2 + 2 M 4 C ) 4hwC^2+2M^2hwC=\frac{h}{M}*\frac{w}{M}*(4M^2C^2+2M^4C) 4hwC2+2M2hwC=Mh∗Mw∗(4M2C2+2M4C)。
两者计算复杂度差别在后半部分,以原文中的参数 h = 56 , w = 56 , C = 96 , M = 7 h=56,w=56,C=96,M=7 h=56,w=56,C=96,M=7为例,多头自注意力后半部分计算复杂度为 2 ( h w ) 2 C = 2 ( 56 ∗ 56 ) 2 ∗ 96 = 1888223232 2(hw)^2C=2(56*56)^2*96=1888223232 2(hw)2C=2(56∗56)2∗96=1888223232,窗口多头自注意力后半部分的计算复杂度为 2 M 2 h w C = 2 ∗ 7 2 ∗ 56 ∗ 56 ∗ 96 = 29503488 2M^2hwC=2*7^2*56*56*96=29503488 2M2hwC=2∗72∗56∗56∗96=29503488。两者相差64倍。
此外,Swin Transformer使用相对位置编码来避免注意力运算未考虑token顺序的问题。与绝对位置编码直接加在输入特征图上不同,相对位置编码以偏执形式存在参与注意力权重的计算,其公式如下:
A
t
t
e
n
t
i
o
n
(
Q
,
K
,
V
)
=
S
o
f
t
M
a
x
(
Q
K
T
d
k
+
B
)
V
Attention(Q,K,V)=SoftMax(\frac{QK^T}{\sqrt{d_k}}+B)V
Attention(Q,K,V)=SoftMax(dkQKT+B)V
详情请参考我关于绝对位置编码和相对位置编码的博客。
2.2.2 滑动窗口多头自注意力
采用窗口多头自注意力时,每个窗口都是独立的,会导致窗口间的相关信息无法被捕捉。例如一个目标处于多个窗口上,窗口独立进行注意力计算就导致该目标各个部分的相关信息无法被考虑。Swin Transformer引入滑动窗口来解决这一问题。
2.2.2.1 窗口滑动
对于 M ∗ M M*M M∗M的窗口,滑动方向为右下,向右移动 ⌊ M 2 ⌋ \lfloor\frac{M}{2}\rfloor ⌊2M⌋个像素点,向下移动 ⌊ M 2 ⌋ \lfloor\frac{M}{2}\rfloor ⌊2M⌋个像素点。
下图是窗口高宽为 4 ∗ 4 4*4 4∗4时窗口滑动前后的窗口分割情况(因为是向右下滑动,所以我在图中增加了左上方的窗口):

可见,经滑动之后的窗口中可能包含滑动前多个窗口的内容。例如,滑动后的中心窗口就包含滑动前的4个窗口中的内容。该操作从一定程度上缓解了相关信息完全丢失的问题。
2.2.2.2 窗口移位与掩码
不过,滑动后各个窗口大小不一,只有在padding后才能组成tensor进行并行运算。以上图为例,原本只有4个 4 ∗ 4 4*4 4∗4的窗口,padding后会产生9个 4 ∗ 4 4*4 4∗4的窗口,这无疑增加了很多计算负担。Swin Transformer通过移位和掩码解决了该问题。
移位流程如下:

可见, A , B , C A,B,C A,B,C均为左上方新增窗口向右下滑动时产生的窗口,因此 A , C A,C A,C的高度为 ⌊ M 2 ⌋ \lfloor\frac{M}{2}\rfloor ⌊2M⌋, A , B A,B A,B的宽度为 ⌊ M 2 ⌋ \lfloor\frac{M}{2}\rfloor ⌊2M⌋, C C C的宽度为 w − ⌊ M 2 ⌋ w-\lfloor\frac{M}{2}\rfloor w−⌊2M⌋, B B B的高度为 h − ⌊ M 2 ⌋ h-\lfloor\frac{M}{2}\rfloor h−⌊2M⌋。
这样,所有新的窗口大小都是统一的 M ∗ M M*M M∗M。但是这引入了另一个问题,同一窗口内包括原本不应相互计算注意力的内容。 例如上图中的右下角窗口,同时包含 A , B , C , D A,B,C,D A,B,C,D四个部分的内容,但 A A A原本在左上角,与 B B B的下侧、 C C C的右侧、 D D D的右下侧一般是没有联系的。就像一张仅包含天空和草地的图片, A , C A,C A,C是天空, B , D B,D B,D是草地, A A A不必与 B , D B,D B,D进行注意力计算。
于是Swin Transformer又引入了掩码。首先给移位后的各个窗口一个编号,如下图:
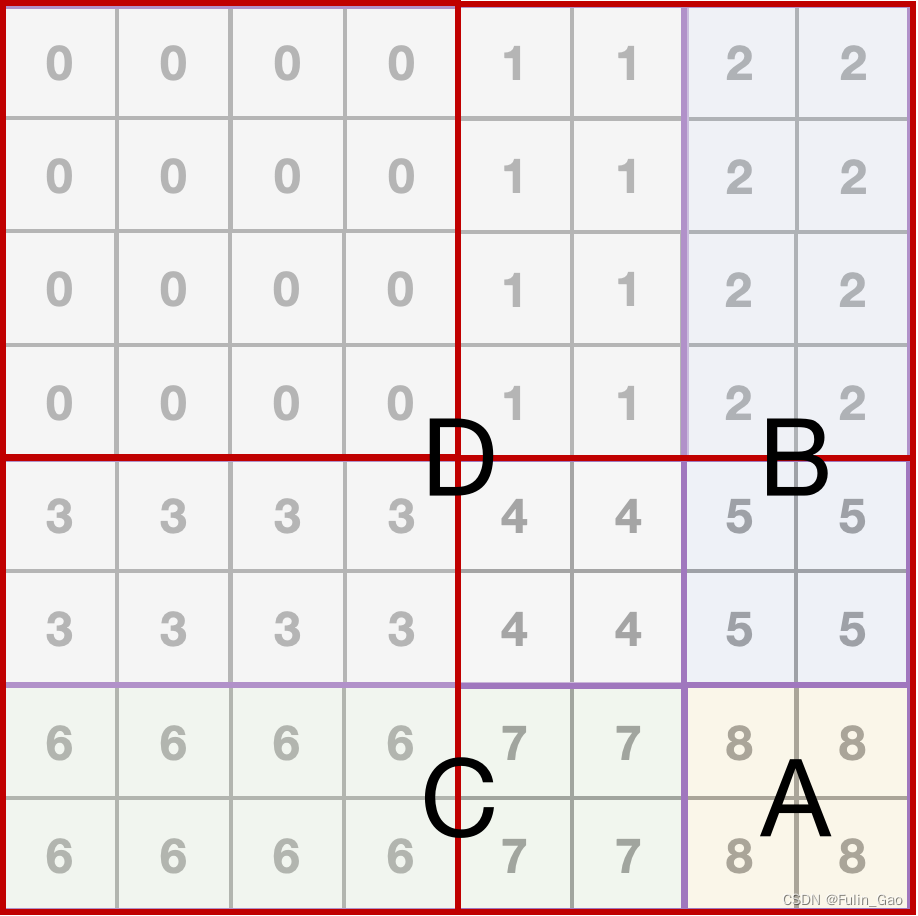
然后给每个窗口每个像素点一个掩码矩阵,如下图(以右下角窗口中两个像素点为例):

掩码矩阵中仅有两种值,0和-100。与查询像素点属于同一编号的像素点对应掩码为0,否则为-100。窗口注意力会计算每个像素点与所有像素点间的相似度,所以窗口中有几个像素点就有几个掩码矩阵,每个掩码矩阵都与窗口大小一致。
这个掩码矩阵像相对位置偏执一样被施加在注意力计算相似度的公式中,如下:
A
t
t
e
n
t
i
o
n
(
Q
,
K
,
V
)
=
S
o
f
t
M
a
x
(
Q
K
T
d
k
+
B
+
M
a
s
k
)
V
Attention(Q,K,V)=SoftMax(\frac{QK^T}{\sqrt{d_k}}+B+Mask)V
Attention(Q,K,V)=SoftMax(dkQKT+B+Mask)V
我们不考虑相对位置偏执 B B B,相似度 Q K T d k \frac{QK^T}{\sqrt{d_k}} dkQKT+掩码 M a s k Mask Mask经SoftMax产生效果如下:

可见,对于橙色框中像素点来说,同编号的像素点与其的相似度没有被改变,其它像素点相似度被减去100。因相似度矩阵中的值都比较小,减去100相当于变成一个很小的数,经SoftMax后其值接近于0。
在各个窗口上计算完多头自注意力后,按照之前移位流程逆向复原,滑动窗口多头自注意力就完成了。
综上,移位操作使并行运算成为可能,掩码操作使注意力计算不跨窗口。
2.3 Patch Merging
Swin Transformer Block不改变特征图尺寸,Patch Merging起到使特征图缩小2倍、通道数放大2倍的作用。
以大小为 4 ∗ 4 4*4 4∗4、单通道的特征图为例,Patch Merging的过程如下图:
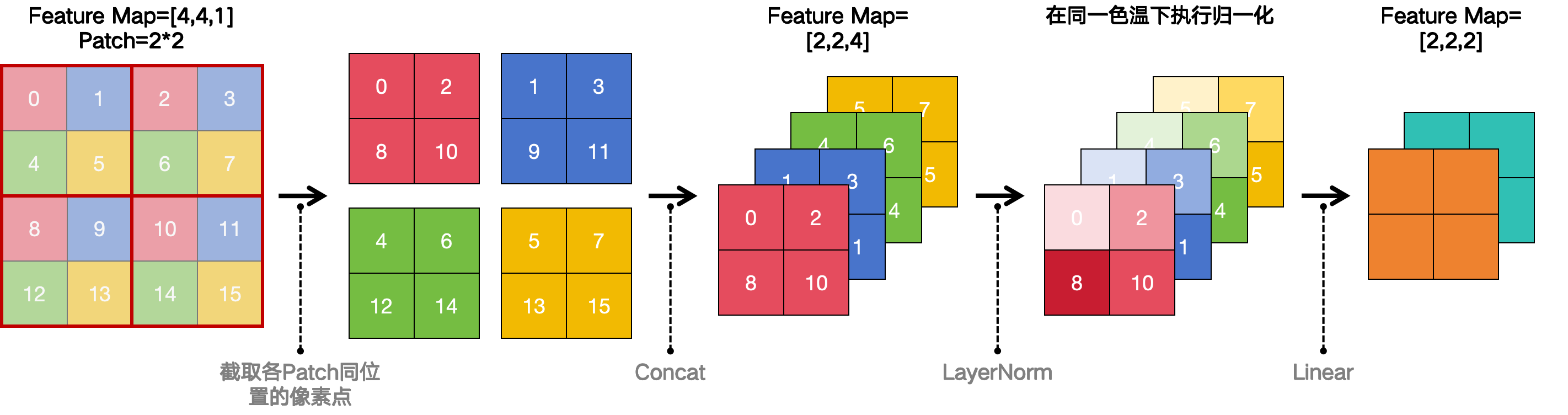
无论特征图是多大,Patch Merging时Patch的高宽均为 2 ∗ 2 2*2 2∗2。截取各Patch同相对位置的像素点,之后将截取结果拼接到一起形成新的特征图。假设原特征图为 [ H , W , C ] [H,W,C] [H,W,C],则中间特征图为 [ H 2 , W 2 , 4 C ] [\frac{H}{2},\frac{W}{2},4C] [2H,2W,4C]。 之后对中间特征图每个像素点所有通道分别执行归一化,并经过一次全连接线性映射将每个像素点的通道数减半。最后特征图为 [ H 2 , W 2 , 2 C ] [\frac{H}{2},\frac{W}{2},2C] [2H,2W,2C]。
致谢:
本博客仅做记录使用,无任何商业用途,参考内容如下:
Swin-Transformer中MSA和W-MSA模块计算复杂度推导
Swin Transformer论文精读【论文精读】
Swin-Transformer网络结构详解