FedSA:一种处理 non-IID 数据 的 过时感知 异步联邦算法
1. 论文信息
FedSA:A staleness-aware asynchronous Federated Learning algorithm with non-IID data,Future Generation Computer Systems,2021.7,ccfc
是 AFL 的经典 baseline 之一
2. Introduction
背景:异步联邦学习中,不同设备计算、通信资源不同,数据分布也不同,在这种情况下,各个设备的模型训练效率不同,导致这些模型更新上传到服务器的时间也不同。一些更新可能基于较早的全局模型,不能很好的反映当前的模型状态,就认为是“过时”。
挑战:
- 跨设备的 non-iid 数据
- 慢收敛,过时问题
贡献点:
- 通过使用一个异步相关参数 统一同步和异步更新方案 重新定义 FL 。从理论上分析了这种新形式,并找到了实用的优化策略。
-
- 1) 两阶段训练策略,一阶段加速训练、减少通信开销;二阶段强调模型稳定性和准确性;
- 2) 各阶段关键超参数的最优选择策略,保证效率和鲁棒性。
- 在理论保证基础上,提出一种新的异步联邦学习算法 FedSA
- 在非 IID 和 IID 数据上实验,在陈旧设备上达到了卓越鲁棒性,也得到了 sota( state-of-the-art) 的 收敛速度
。
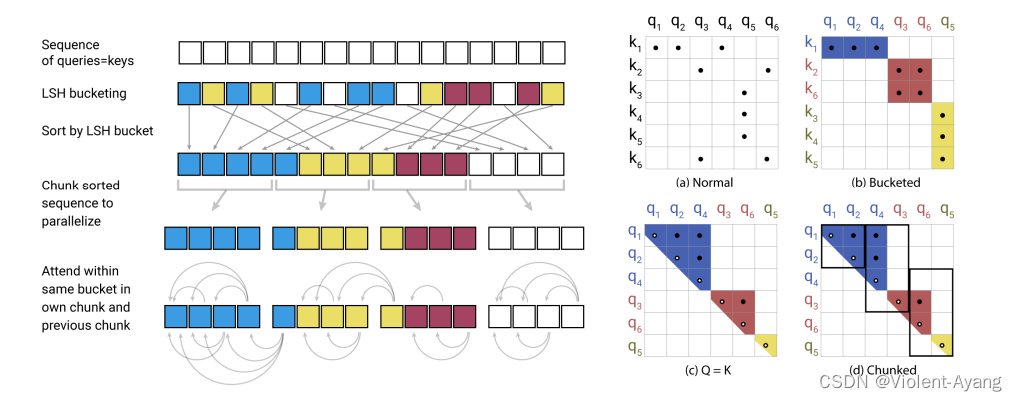
3. 问题描述:System model/架构/对问题的形式化描述

同步FL
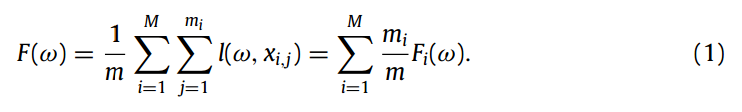
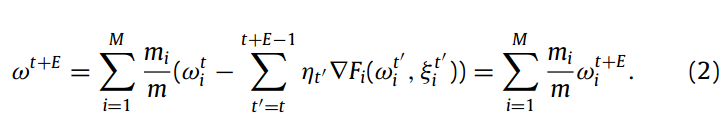
异步FL

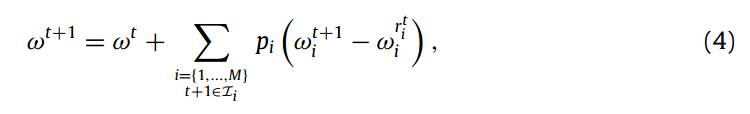
4. 解决方法
4.1. 执行流程:


4.2. 挑战问题怎么解决:
4.2.1. 两阶段的训练策略
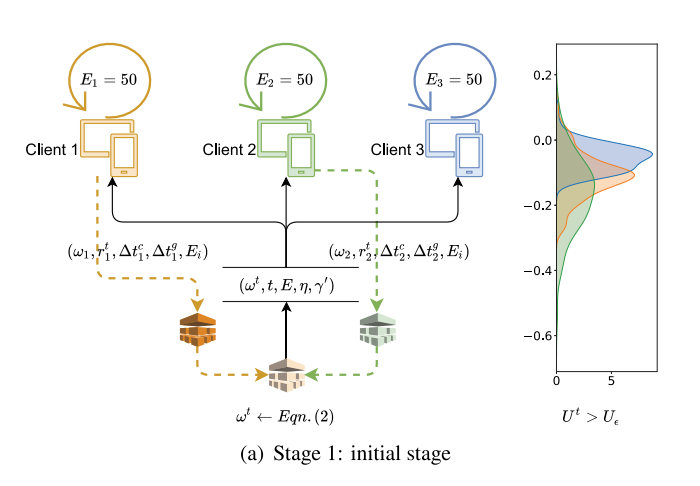
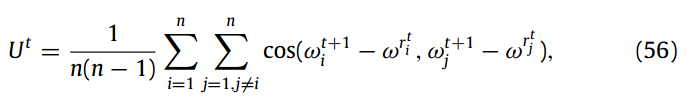
initial stage:此阶段 局部误差 对 全局误差的影响最大,要尽可能地降低局部误差的影响。客户端选用 较大的本地周期 E
![]()
,保证客户端能进行充足的训练,减少通信开销,快速逼近全局最优
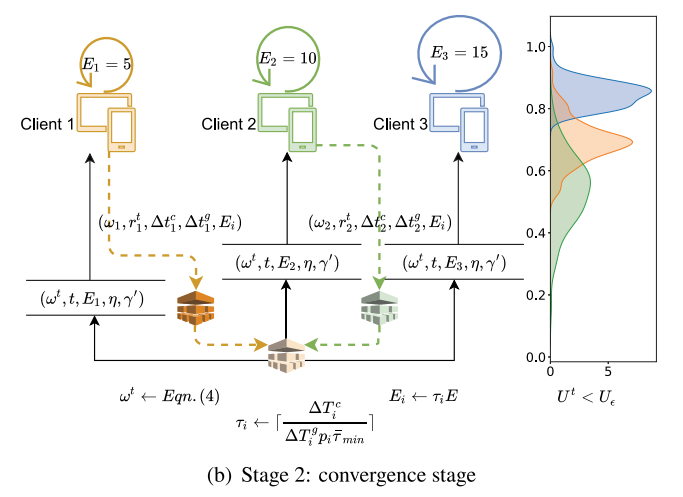
convergence stage:随着局部模型逐渐逼近最优模型,局部误差的减少将放缓,而局部-全局误差开始变得更加显著。一旦模型更新之间的相似度降低到某个阈值以下
![]()
,表明初始化阶段已经完成,算法进入收敛阶段。FedSA算法开始更加关注陈旧性问题,通过 减小本地周期 E 和使用 衰减学习率 来精细化调整模型参数,同时,τ参数开始发挥更直接的作用,根据设备的计算和通信成本来动态调整上传频率,以减少陈旧性的影响,实现更精确的全局模型。
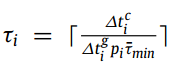
![]()
4.2.2. 陈旧感知
一阶段:计算相似性
![]()
二阶段:根据
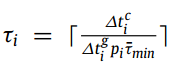
![]()
4.3. 性能保证(performance guarantee):理论分析,使用什么理论,怎么分析/解决
尝试推导,还是不太行
定理1:

在训练过程的开始阶段,局部误差占全局误差的主导地位,即局部误差足够大于局部-全局误差:
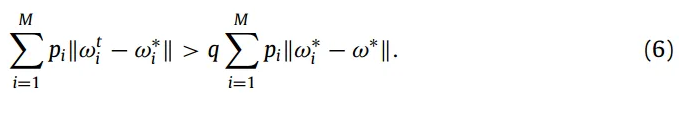
- 减少局部误差可以在早期有效地减少全局误差,并且由于ω ti和ω∗i都是设备中的局部模型,因此局部误差可以在不通信的情况下局部优化。
- 当局部误差完全最小化时,不再支配全局误差。因此,优化局部-全局误差在之后变得至关重要。然而,当假设5成立时,ω∗和ω∗i是唯一的(即给定特定问题的常数),不能被优化。因此,这意味着应该在需要通信的地方直接优化全局误差。
-
- 初始阶段最小化局部误差:在初始阶段结束之前设置任意大的 E。
- 然而,在没有任何通信的情况下,很难感知到这个阶段的何时停止时刻。为了保持足够的通信,需要一个相对较小的历元数。最后,需要一个指标来决定何时通过这些通信停止初始阶段。
- 收敛阶段的策略
-
-
- 局部历元E的数量,
- I 中与异步相关的参数τ
- 学习率
- 选择这些参数的动机是:1)I中的E和τ之间存在相互作用,2)对于非iidness的同步FL(即FedAvg),可以通过学习率衰减来保证收敛,这也适用于异步模型。
-
定理2:
设假设 1-4 满足,定义c、β、σi、χ。我们用F *和F * i分别表示目标函数 F 和 Fi 的最小值。我们将收敛阶段开始时的全局模型定义为 ω t0。然后给定最大时间步长 T,对于任意固定个数的局部历元 E,以及 固定的学习率η¯≤1/4 β,扩展FL形式的误差满足该界
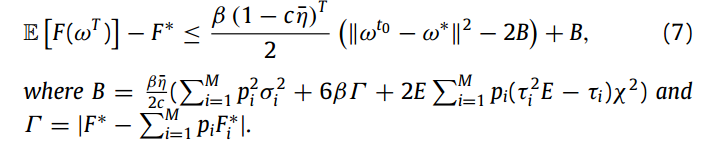
定理3:
设定理2中除固定学习率条件外,其余条件成立,其中定义γ和ν。对于所有t = 1,2,…,将 学习率衰减 为
![]()
,则扩展FL形式的误差满足该界

定理 2 和定理 3 分别证明了 固定学习率 和 衰减学习率 下扩展FL形式的收敛界。定理3 证实了在 非iid 和异步情况下,采用衰减学习率ηt = 2/c (γ + T), FL的扩展形式达到了与 标准SGD 相似的收敛速率 O(1/t) (被认为是最优的)。此外,当 χ 接近于零(即IID情况)时,得到与 O(1/t) 相同阶的收敛速率。定理3 采用衰减学习率 对 IID 和 非IID 情况都适用。
定理4:
设定理3中的条件成立。将 Tε 表示为达到给定误差界的最小全局历元数(ε > 0)。给定 Tε ,假设扩展FL形式的误差界满足
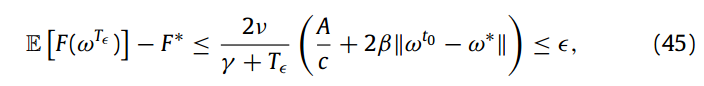
通信轮次
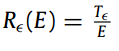
可以被 E 最小化
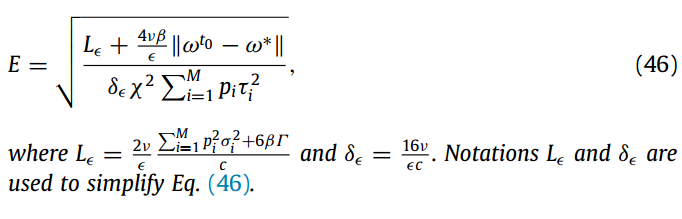
定理4 给出了 E 的最佳选择,减少与非iid数据的 通信开销 (即χ i = 0)。在整个训练过程中,E 的选择不是静态的。初始阶段结束时,E 与全局误差∥ω t0−ω∗∥成正比。表明在收敛阶段,由于∥ω t0−ω∗∥<∥ω 0−ω∗∥,我们将选择一个较小的E。
到目前为止,上述定理和评论主要集中在统计异质性的收敛和通信上。从定理4可知,在 Rϵ (E) 通信轮之后,最优间隙的期望将收敛到一个 ϵ 邻域。为估计实现 ϵ 界所需的总体训练时间,定义 ∆tgi为局部优化器一次更新的时间成本,∆tci为设备i与服务器之间一次通信的时间成本,对于所有设备,定义客户i的总时间成本为
![]()
![]()
,整个FL系统的总时间成本为
![]()
定理5:设假设1 ~ 4成立,通过选择最优τi,得到最小时间代价
![]()
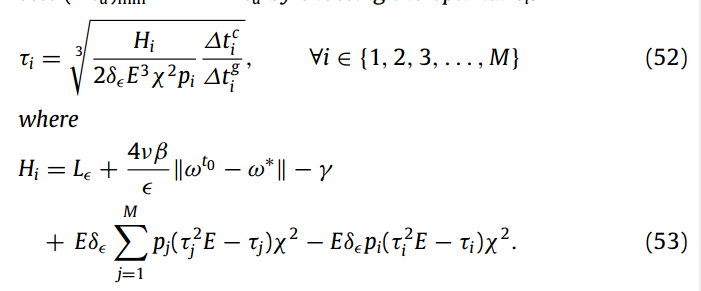
定理5 给出了选择 τ 的策略。实际上,当设备的连接速度较慢 (即∆tci较高) 时,可以通过设置较大的 τ 来减少通信次数,而当设备速度较慢 (即∆tgi较高) 时,选择较小的τ。此外,当设备具有较大的数据量 (即 pi 很大) 时,设置较小的τ,较大的τ可能会降低训练质量。
5. 效果:重点是实验设计,每一部分实验在验证论文中的什么结论
5.1. 实验设置

5.2. 超参数确定实验
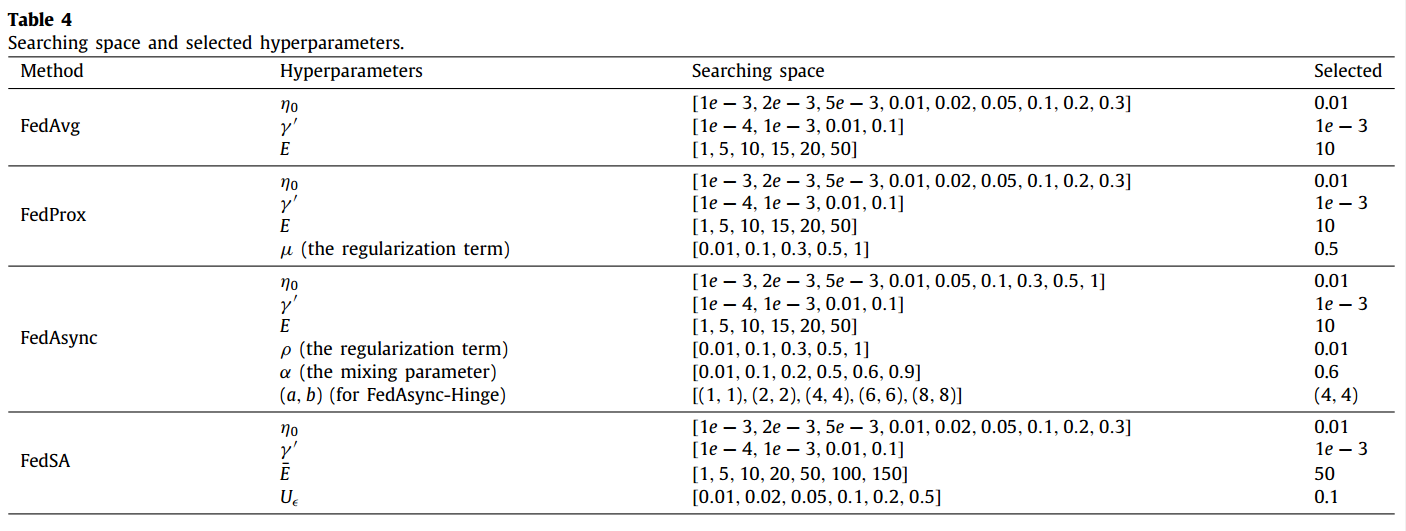
对每个算法的超参组合进行网格搜索,找到表现最佳的一组,进行接下来的实验
5.3. 对比实验
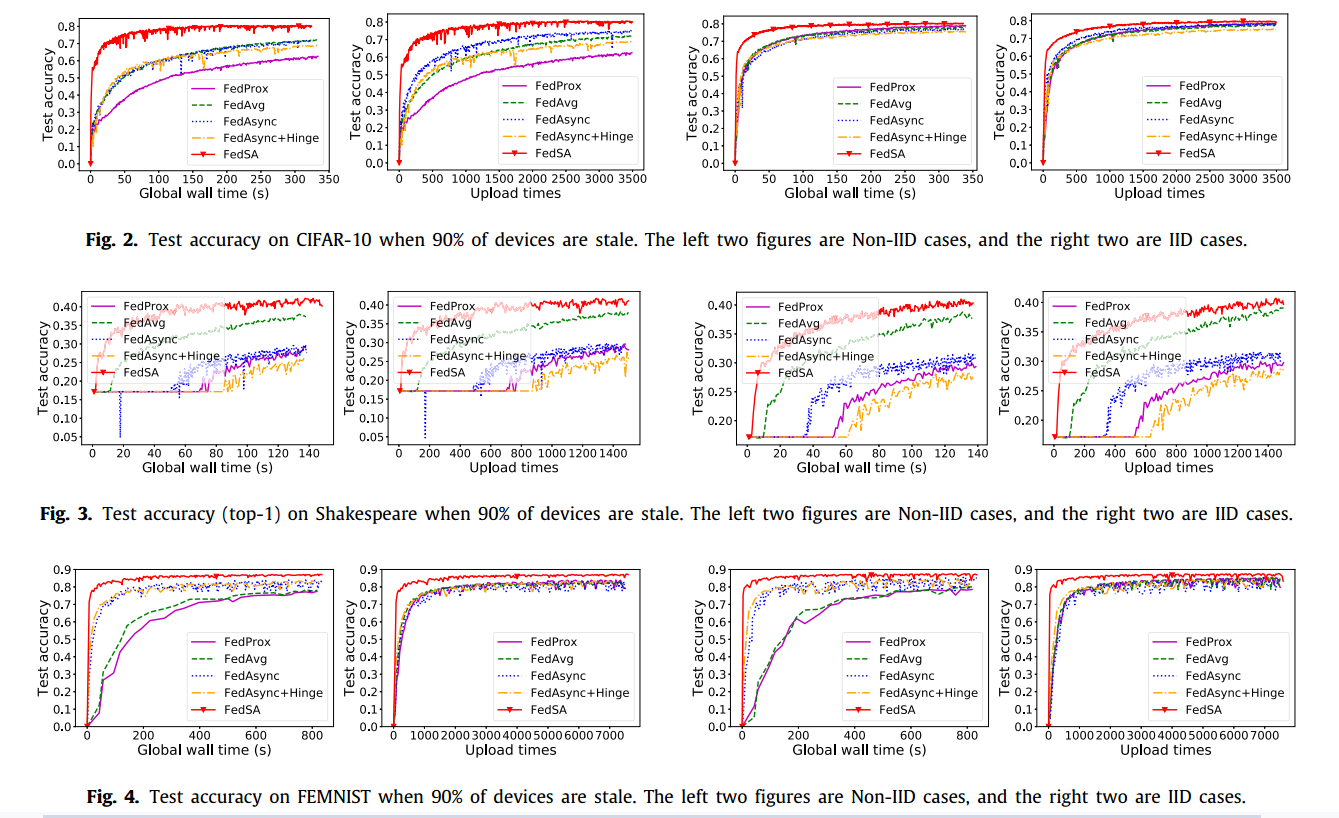
左边是non-iid 右边是iid
验证FedSA在收敛和通信方面的效率。图2、图3、图4展示了在陈旧设备占90%的情况下,FedSA和四个基线在非IID和IID数据上的测试精度。FedSA在收敛和通信方面都优于其他基线,特别是在非iid情况下。FedSA在非IID情况下的表现与IID情况下保持相同的水平,而其他基线在非IID情况下与IID情况相比恶化了很多。
在定理3中,当χ接近于零(即IID情况)时,我们得到与标准SGD相似的O(1 T)收敛速率,这被认为是最优的。
此外,FedSA在初始阶段和收敛阶段之间的过渡阶段,即在训练刚开始的时候,准确率急剧提高,这大大减少了训练早期的通信时间
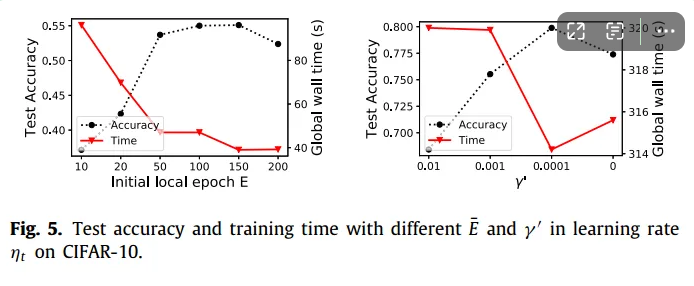
图5(a)测试了初始阶段不同 E 的性能。
结果验证了定理1和备注1中得到的选择较大E(例如¯E = 150)的有效性。最后,
图5(b)在收敛阶段验证了学习率衰减策略,显示了不同γ′对学习率ηt的影响,验证了定理3,即学习率衰减是收敛的关键。
综上所述,上述实验验证了所提出的两阶段训练方法的可行性和合理性

用陈旧的设备验证了鲁棒性。图6 (a)和(b)显示了不同陈旧设备数量下的性能。可以看出,即使在90%的设备陈旧的情况下,FedSA仍然是稳定的,并且在测试精度和全局训练时间上都优于AFL基线(即FedAsync)。当陈旧设备从60%增加到90%时,测试精度的绝对损失仅小于2%。
当设备陈旧率超过20%时,FedSA的总训练时间小于基线。通过定理5和注释4中提出的自适应τ,验证了FedSA对过期效应的鲁棒性。
6. (备选)自己的思考
- 因为相似性的判断是针对已经到达服务器并处于等待聚合状态的模型进行的。文章的设定条件是 Q 队列中只要有两个及以上的模型更新就进行相似性比较,相似时间到达的模型更新直觉上资源以及计算能力都是相似的(让最相似的达到最不相似,训练充分)
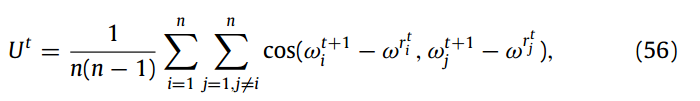
可不可以从比较相似性的条件入手(模型更新数量,或者新的比较条件)
- 缺点:超参很多,感觉受超参影响很大
- 学不明白,讲不明白,这次汇报只要比上周好一点就是进步!欣宝加油!!!



![BUU-[极客大挑战 2019]Http](https://img-blog.csdnimg.cn/img_convert/e17de46ff75804a929240042b3e08c63.png)