大型Transformer模型通常在许多任务上都能达到最先进的结果，但是训练这些模型的成本可能会非常高昂，特别是在处理长序列时。我们引入了两种技术来提高Transformer的效率。首先，我们用一种使用局部敏感哈希的点积注意力替换了原来的点积注意力，将其复杂度从O(L^2)改变为O(L log L)，其中L是序列的长度。此外，我们使用可逆的残差层代替了标准残差，这允许在训练过程中只存储一次激活，而不是N次，N是层的数量。由此产生的模型，即改革者模型，在性能上与Transformer模型相当，同时在长序列上更加内存高效，速度更快。

1 引言

Transformer架构（Vaswani et al., 2017）在自然语言处理中被广泛使用，并在许多任务上取得了最先进的结果。为了获得这些结果，研究人员已经转向训练越来越大的Transformer模型。在（Shazeer et al., 2018）中报告的最大配置中，每层的参数数量超过0.5B，而在（Al-Rfou et al., 2018）中，层数高达64。Transformer模型还用于越来越长的序列。在（Liu et al., 2018）中，单个示例中处理的文本令牌数量高达11,000个，而在处理其他模态，如音乐（Huang et al., 2018）和图像（Parmar et al., 2018）时，更长的序列更是常见。这些大规模长序列模型虽然取得了出色的结果，但对资源的压力如此之大，以至于一些人认为这种趋势正在破坏自然语言处理研究。许多大型Transformer模型只能在大型工业研究实验室中实际训练，而且使用模型并行训练的这些模型甚至不能在单个GPU上微调，因为它们的内存需求需要多加速器硬件设置，即使是单个训练步骤也是如此。

大型Transformer模型真的需要如此巨大的资源，还是仅仅是效率低下？考虑以下计算：在最大报告的Transformer层中使用的0.5B参数占用2GB的内存。对于64K个令牌，嵌入大小为1024，批量大小为8的激活，占64K × 1K × 8 = 0.5B浮点数，需要另外2GB的内存。如果我们的内存使用仅按层计算，那么我们应该很容易地在单个加速器上适应一个大型Transformer，即使是在长度为64K的序列上。此外，用于训练BERT的整个语料库仅需要17GB的存储空间。那么，为什么我们甚至不能在单台机器上微调这些模型呢？

上述估计仅包括每层内存和输入激活的成本，并没有考虑到Transformer中的以下主要内存使用来源。

• 在具有N层的模型中，内存是单层模型的N倍，因为需要为反向传播存储激活。

• 由于中间前馈层的深度dff通常比注意力激活的深度dmodel大得多，因此它占据了内存使用的很大一部分。

• 对于长度为L的序列，注意力在计算和内存复杂度上都是O(L^2)，在单个64K令牌的序列上就可以耗尽加速器的内存。

我们引入了改革者模型，它使用以下技术解决了这些问题：

• 可逆层，最初在Gomez等人（2017）中引入，允许在整个模型中只存储一份激活，因此N因子消失了。

• 在前馈层内分割激活并在块中处理它们，去除了dff因子，并在前馈层内节省了内存。

• 基于局部敏感哈希的近似注意力计算将注意力层中的O(L^2)因子替换为O(L log L)，从而允许操作长序列。

我们研究了这些技术，并展示了它们与标准Transformer相比对训练过程几乎没有影响。实际上，分割激活只影响实现；它在数值上与Transformer中使用的层是相同的。应用可逆残差而不是标准残差确实改变了模型，但在我们实验的所有配置中对训练的影响可以忽略不计。最后，注意力中的局部敏感哈希是一个更重大的变化，它可能会根据使用的并发哈希数量影响训练动态。我们研究了这个参数，并找到了一个既有效又产生接近完整注意力结果的值。

我们在合成任务、文本任务（enwik8）上进行了实验，该任务的序列长度为64K，以及图像生成任务（imagenet-64生成）上进行了实验，该任务的序列长度为12K。在这两种情况下，我们展示了改革者与使用完整Transformer获得的结果相匹配，但运行速度更快，特别是在文本任务上，并且具有更好的内存效率。

2 局部敏感哈希注意力

点积注意力。Transformer中使用的标准注意力是缩放点积注意力（Vaswani et al., 2017）。输入由维度为dk的查询和键，以及维度为dv的值组成。计算查询与所有键的点积，通过√dk进行缩放，并应用softmax函数以获得值上的权重。在实践中，对一组查询同时计算注意力函数，将它们打包成一个矩阵Q。假设键和值也被打包成矩阵K和V，输出矩阵定义为：
$$\text{Attention}(Q,K,V)=\text{softmax}\left(\frac{Q{K}^T}{\sqrt{d_k}}\right)V$$

多头注意力。在Transformer中，不是使用具有dmodel维键、值和查询的单个注意力函数，而是将查询、键和值线性投影h次，使用不同的、学习的线性投影到dk、dk和dv维度。注意力被并行应用于这些投影版本的查询、键和值，产生dv维的输出值。这些被连接起来，然后再次投影，产生最终值。这种机制被称为多头注意力。

内存高效注意力。为了计算注意力机制的内存使用，让我们专注于方程1中的注意力计算。假设Q、K和V都具有形状[批量大小，长度，dmodel]。主要问题是项QK^T，
它的形状是[批量大小，长度，长度]。在实验部分，我们在长度为64K的序列上训练了一个模型——在这种情况下，即使批量大小为1，这也是一个64K×64K的矩阵，在32位浮点数中将占用16GB的内存。这是不切实际的，并且阻碍了Transformer用于长序列。但重要的是要注意，QK^T 矩阵不需要完全在内存中具体化。注意力确实可以为每个查询qi单独计算，只计算一次softmax(qiK^T √dk)V在内存中，然后在反向传递中需要梯度时重新计算。计算注意力的这种方式可能效率较低，但它只使用与长度成比例的内存。我们使用这种内存高效的注意力实现来运行实验部分中介绍的全注意力基线。

Q、K、V来自哪里？上面描述的多头注意力操作在键、查询和值上，但通常我们只给定一个激活张量A，形状为[批量大小，长度，dmodel]——例如，来自将句子中的令牌嵌入到向量中。

为了从A构建Q、K和V，Transformer使用3个不同的线性层将A投影到Q、K和V，具有不同的参数。对于具有LSH注意力的模型，我们希望查询和键（Q和K）是相同的。这可以通过使用相同的线性层从A到Q和K，以及用于V的另一个单独层来轻松实现。我们称这种行为的模型为共享-QKTransformer。结果表明，即使我们另外规范化键K的长度，共享QK也不会影响Transformer的性能，正如我们在实验部分第5节中所示。

哈希注意力。对于LSH注意力，我们从两个张量Q=K和V开始，形状为[批量大小，长度，dmodel]。我们保持多头机制不变，专注于方程1中的注意力计算。正如已经提到的，主要问题是项QK^T， 它的形状是[批量大小，长度，长度]。但请注意，我们实际上只对softmax(QK^T)感兴趣。由于softmax由最大的元素主导，对于每个查询qi，我们只需要关注K中最接近qi的键。例如，如果K的长度为64K，对于每个qi，我们只需要考虑一个小的子集，比如说32或64个最近的键。这要高效得多，但我们如何找到键中的最近邻呢？

局部敏感哈希。在高维空间中快速找到最近邻的问题可以通过局部敏感哈希（LSH）解决。一种将每个向量x分配到哈希h(x)的哈希方案被称为局部敏感的，如果附近的向量以高概率获得相同的哈希，而远离的向量则不是。在我们的案例中，实际上我们只需要附近的向量以高概率获得相同的哈希，并且哈希桶以高概率具有相似的大小。

我们通过以下方式使用随机投影来实现（见图1）。为了获得b个哈希，我们首先固定一个大小为[dk, b/2]的随机矩阵R。然后我们定义h(x) = arg max([xR; −xR])，其中[u; v]表示两个向量的连接。这种方法是一种已知的LSH方案（Andoni et al., 2015），并且易于实现和应用于批量向量。

LSH注意力。了解我们的LSH方案和哈希注意力的一般思想后，我们现在将正式定义本文中使用的LSH注意力。我们首先重写正常注意力的方程（1），一次针对单个查询位置i：

$$o_i=\sum _{j\in {\hat{P}}_i}\exp \left(\frac{q_i\cdot k_j}{\sqrt{d_k}}-z(i,P_i)\right)v_j$$

我们引入符号Pi来表示查询在位置i关注的集合，z表示分割函数（即softmax中的归一化项）。为了清晰起见，我们还省略了√dk的缩放。

为了批处理的目的，我们通常在更大的集合上执行注意力 $$h(x)=\arg \max ([xR;-xR])$$，同时掩盖不在Pi中的元素：

P i = { j : h ( q i ) = h ( k j ) } P_i = \{j : h(q_i) = h(k_j)\} Pi​={j:h(qi​)=h(kj​)}

其中 m(j, Pi) = ∞ 如果 j ∉ Pi 否则为 0

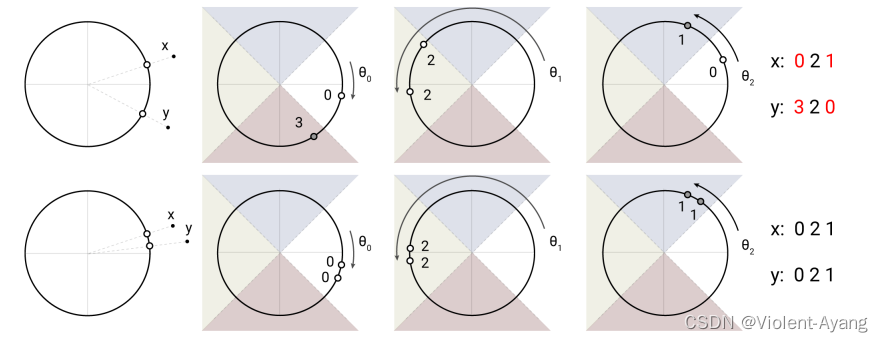
图1： 一个角度局部敏感哈希使用随机旋转的球面投影点通过在有符号轴投影上求argmax来建立桶。在这个高度简化的2D描述中，两个点x和y不太可能（上图）为三个不同的角哈希共享相同的哈希桶，除非它们的球面投影彼此非常接近（下图）。

现在我们转向LSH注意力，我们可以认为它通过只允许在一个哈希桶内注意力来限制查询位置i可以关注的项目集合Pi。

P i = { j : h ( q i ) = h ( k j ) } P_i = \{j : h(q_i) = h(k_j)\} Pi​={j:h(qi​)=h(kj​)}

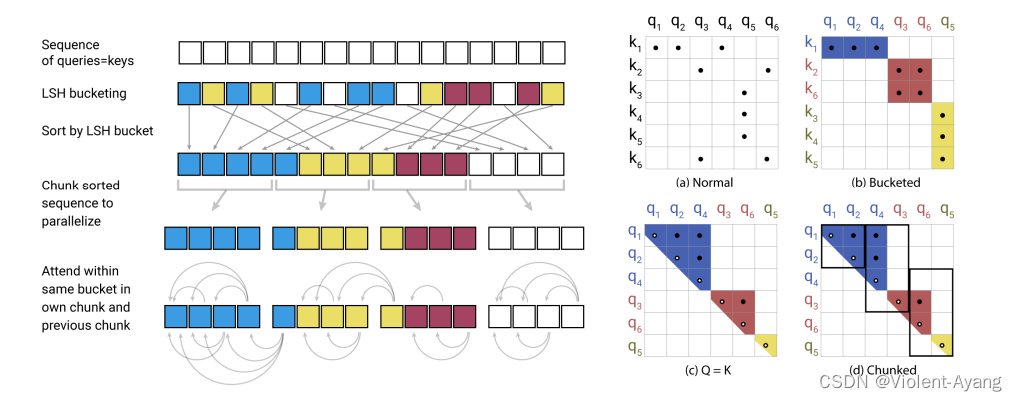
图2(a-b) 显示了全注意力与哈希变体的图解比较。部分(a)描述了全注意力的注意力矩阵通常是稀疏的，但计算并没有利用这种稀疏性。在(b)中，查询和键已根据它们的哈希桶进行了排序。由于类似项以高概率落在同一个桶中，可以通过只允许在每个桶内注意力来近似全注意力模式。

这种表述中的哈希桶往往是大小不一的，这使得跨桶批处理变得困难。此外，桶内的查询数和键数可能不相等——事实上，一个桶可能包含许多查询但没有键。为了缓解这些问题，我们首先确保 h(k_j) = h(q_j) 通过设置 k_j = q_j / |q_j|。接下来，我们根据桶号对查询进行排序，在每个桶内按序列位置排序；这定义了一个排列，其中 i → s_i 在排序后。在排序后的注意力矩阵中，来自同一桶的对将聚集在对角线附近（如图2c所示）。我们可以遵循一种批处理方法，其中排序后的连续查询块m个（排序后）彼此关注，并且回溯一个块（图2d）。按照我们之前的符号，这对应于设置：

P ^ i = { j : ∣ s i / m − s j / m ∣ ≤ 1 } \hat{P}_i = \{ j : |s_i / m - s_j / m| \leq 1 \} P^i​={j:∣si​/m−sj​/m∣≤1}

如果 max |P_i| < m，那么 P_i ⊆ \hat{P}_i。在实践中，我们设置 m = 2^l / n_buckets（其中l是序列长度）。平均桶大小是 l / n_buckets，我们假设一个桶增长到两倍大小的概率足够低。LSH注意力的整个过程在图2中进行了总结。

多轮LSH注意力。 使用哈希，总是存在一个小概率，即相似项仍然落在不同的桶中。这个概率可以通过使用n_rounds个不同的哈希函数进行多轮哈希来降低，如下所示：

P i = ⋃ r = 1 n rounds P i ( r ) where P i ( r ) = { j : h ( r ) ( q i ) = h ( r ) ( k j ) } P_i = \bigcup_{r=1}^{n_{\text{rounds}}} P_i^{(r)} \quad \text{where} \quad P_i^{(r)} = \{ j : h^{(r)}(q_i) = h^{(r)}(k_j) \} Pi​=r=1⋃nrounds​​Pi(r)​wherePi(r)​={j:h(r)(qi​)=h(r)(kj​)}

多轮情况本质上涉及并行执行n_rounds次LSH注意力；程序的细节在附录A中描述。

共享-QK注意力的因果掩蔽。 在Transformer解码器中，掩蔽（在方程3中由m(j, Pi)表示）用于防止位置关注未来。要在LSH注意力中实现掩蔽，我们与位置索引关联每个查询/键向量，使用与排序查询/键向量相同的排列对位置索引进行重新排序，然后使用比较操作来计算掩蔽。

2.1 合成任务上的分析

为了验证LSH注意力的性能并研究其行为，我们从以下合成任务开始：复制一系列符号。在这个任务中，每个训练和测试示例都具有形式0w0w，其中w ∈ {1, . . . , N}∗是1到N（在我们的实验中使用N = 127）的符号序列。下面给出了一个长度为3的w单词的示例。

示例：0 19 113 72 0 19 113 72

为了研究LSH注意力，我们在每个w长度为511的示例上训练了一个语言模型（因此整个输入0w0w的长度为1024）。由于这是一个语言建模任务，我们总是根据之前的所有符号预测下一个符号，但我们掩盖了损失和准确性，只考虑输入的后半部分的位置上，即可实际预测的位置。

一个单层Transformer模型可以完美解决（达到100%的准确性和0的损失）这个任务。但请注意，它需要非局部注意力查找，因此任何依赖于有限跨度的稀疏注意力模型都无法解决。为了使训练既简单又快速，但又类似于NLP中使用模型，我们使用了一个单层Transformer，其中dmodel = dff = 256和4个头。我们在4种不同设置下训练了150K步：使用全注意力、nrounds = 1、nrounds = 2和nrounds = 4的LSH注意力。

从表2中总结的结果中我们可以看到，用全注意力训练的模型可以立即使用LSH注意力，但会有一定准确性的损失。当从头开始用LSH注意力训练时，使用4个哈希训练的模型也几乎达到了完美的准确性。有趣的是，当用8个哈希评估时，准确性变得完美。当用2个或1个哈希评估时，准确性会下降。使用较少哈希训练的模型显示出更差的结果，但即使只使用1个哈希训练的模型，在用8个哈希评估时也表现出几乎完美的性能。

3 可逆Transformer

正如上节所示，只要可以接受近似值，就可以将注意力的复杂度从长度的平方降低到线性。但很明显，从表1可以看出，每个字段都以b·nh·l项开始：b·nh·l·dk，或者b·l·dmodel的成本无法避免。实际上，每层之前的激活已经是b·l·dmodel的大小，所以nl层的整个模型的内存使用至少是b·l·dmodel·nl。更糟糕的是：在Transformer的前馈层中，这个上升到b·l·dff·nl。在大型Transformer中，通常设置dff = 4K和nl = 16，所以对于l = 64K，这将再次使用不切实际的16GB内存。

在本节中，我们将展示如何首先通过使用可逆层来处理nl项，然后展示分块如何允许我们处理dff问题。这些方法对内存和时间复杂度的影响在表3中进行了总结。

RevNets。可逆残差网络由Gomez等人（2017）引入，其中展示了它们可以用于图像分类的ResNets。主要思想是允许任何给定层的激活从下一层的激活中恢复，仅使用模型参数。而不是必须检查点中间值以在反向传递中使用，可以从网络的输出到其输入逐层反转层。而一个正常的残差层执行一个函数x → y，它操作一个输入并产生一个输出，并且具有形式y = x + F(x)，一个可逆层处理输入/输出对：(x1, x2) → (y1, y2)，并遵循以下方程：

y1 = x1 + F(x2)
y2 = x2 + G(y1)

一个层可以通过减去（而不是添加）残差来反转：

x2 = y2 − G(y1)
x1 = y1 − F(x2)

可逆Transformer。我们通过将注意力和前馈层组合在revnet块内，将RevNet的思想应用于Transformer。在上面的符号中，F变成一个注意力层，而G变成前馈层。请注意，层归一化（Ba等人，2016）被移动到残差块内部。

Y1 = X1 + 注意力(X2)
Y2 = X2 + 前馈(Y1)

可逆Transformer不需要在每一层存储激活，因此消除了nl项。在第5节中，我们展示了它在使用相同数量的参数时与正常Transformer表现相同；我们通过让x1和x2都具有dmodel的大小来实现这一点。

分块。虽然可逆性涵盖了nl项，但更厚的层仍然可以使用很多内存。特别是前馈层可以使用中间向量，其维度为dff = 4K或更高。然而，前馈层中的计算在序列中的位置是完全独立的，因此可以将计算分成c个块：

Y2 = ∑ Y(1) 2 ; . . . ; Y© 2 = ∑ X(1) 2 + 前馈(Y(1) 1); . . . ; X© 2 + 前馈(Y© 1)

这一层通常通过并行执行所有位置的操作来进行批处理，但是一次操作一个块可以减少内存。在（8）中的反向计算和反向传递也被分成块。除了前馈层，对于具有大词汇表（超过dmodel单词类型的）的模型，我们还分块输出的对数概率，并一次计算序列部分的损失。

分块，大批量和参数重用。有了分块和可逆层，我们在整个网络中用于激活的内存与层数无关。情况并非如此，因为它们的数目随着层数的增加而增长。这个问题通过在该层不计算时将层参数交换到和从CPU内存中移出而得到解决。在标准Transformer中，这将是低效的，因为内存传输到CPU的速度很慢。然而，Reformer中的批量大小乘以长度要大得多，因此使用参数进行的计算量摊销了它们的传输成本。

4 相关工作

在（Vaswani et al., 2017）中引入的Transformer模型已广泛用于自然语言任务，并且进一步扩展到模拟多样化数据，如乐谱（Huang et al., 2018）和图像（Parmar et al., 2018; Ramachandran et al., 2019）。最值得注意的是，这个模型类别已成功应用于自监督训练非常大的语言模型（Devlin et al., 2018; Radford et al., 2019）。

鉴于最先进的序列模型的巨大计算需求，人们越来越有兴趣找到减少Transformer模型内存占用和计算需求的方法。除了标准方法，如精度降低和梯度检查点（Sohoni et al., 2019），还探索了Transformer模型自注意力机制的更有效版本（Sukhbaatar et al., 2019a;b）。

特别是，利用注意力层中的稀疏性已经证明是有益的。OpenAI介绍了稀疏Transformer（Child et al., 2019），它利用注意力的因子化稀疏表示。使用乘积键注意力来增加键空间也已用于减少前馈层的内存需求，而不会损失性能（Lample et al., 2019）。

据我们所知，局部敏感哈希（LSH）以前没有直接应用于Transformer注意力层。但是，先前使用神经网络的外部内存的工作已经处理了大尺寸的内存。记忆网络的原始实现（Weston et al., 2014）和后来的工作在扩展它（Bordes et al., 2015; Chandar et al., 2016）中使用了数百万大小的内存。这样做的代价是内存必须在训练之前固定。此外，由于在训练开始时，模型不太可能正确查询内存，因此使用强监督来鼓励模型查询有用的内存位置。这些提示要么是任务提供的额外监督信息，要么像Hill等人（2015）中那样通过启发式确定。在Santoro等人（2016）中，已经取消了在训练之前必须固定内存的要求，代价是内存大小，后来又由Rae等人（2016）缓解了。最后一篇论文考虑了包括LSH和随机kd树在内的近似最近邻内存查找，但仅限于在外部内存中查找。

5 结论

Reformer结合了Transformer的建模能力，并且具有一个可以高效执行长序列的架构，即使对于具有大量层的模型，内存使用也很小。我们相信，这将有助于大型、参数丰富的Transformer模型变得更加广泛和易于访问。此外，处理长序列的能力为Reformer在许多生成任务上的使用打开了道路。除了生成非常长的连贯文本，Reformer还可以将Transformer模型的力量带到其他领域，如时间序列预测、音乐、图像和视频生成。