引入

概述

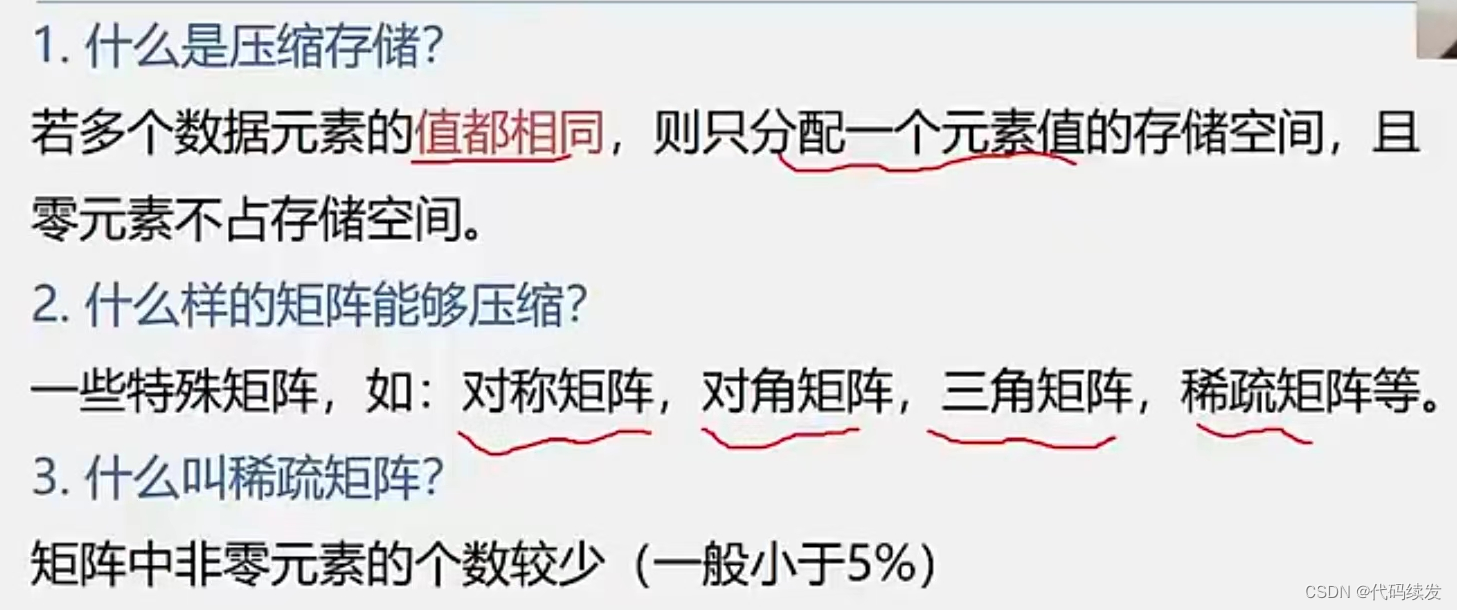
特殊矩阵的压缩

对称矩阵

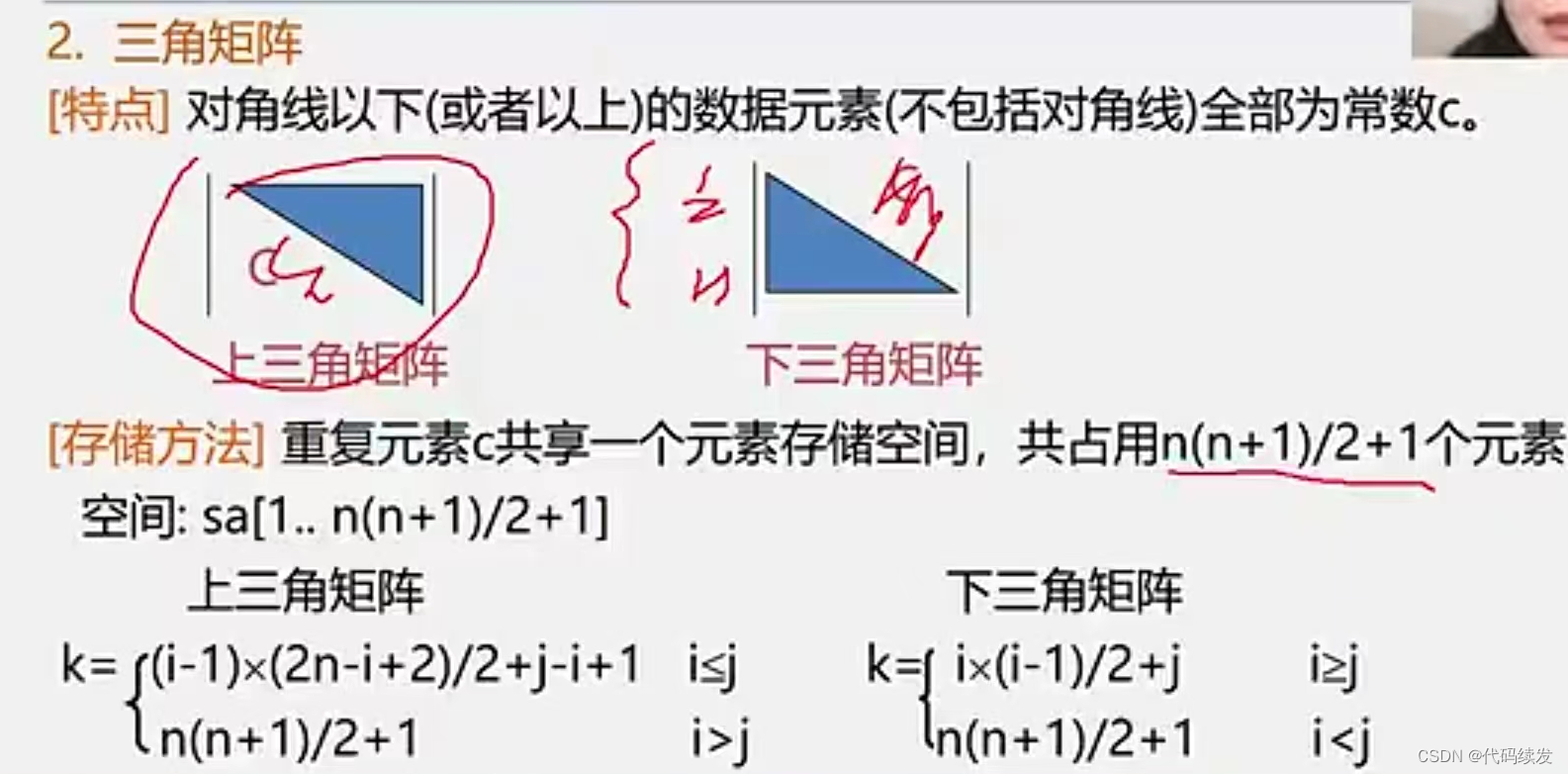
三角矩阵

上三角矩阵：上三角区的元素不同，下三角区的元素相同。

                     存储不同元素的上三角区(计算前i-1行的所有元素之和+(j-i+1)[i行的列数]-1[下标由0开始],即以下标为0开始存储的下标)+一个相同元素(下三角区)

下三角矩阵：下三角区元素不同，上三角区的元素相同

                       存储不同元素的下三角区+一个相同元素(上三角区)

结合王道视频的推理补充-数组下标由0开始存储 

而王卓老师讲解的是下标由1开始存储：在王道基础上下标+1即可

对角矩阵

容量下标3n-3=3*(n-2)有n-2行是3个元素+2*2有两行是2个元素-1下标从0开始=3*(n-2)+4-1

前i-1行=第一行2个元素+第2行到i-1行3个元素，即前i-1行共有3(i-1)-1个元素

第i行共有j-i+1列数(如a11第1行有1-1+1列)

aij对应于B中存储(B下标由0开始)的下标为=前i-1行+第i行的列数=3(i-1)-1+j-i+1=2i+j-3

稀疏矩阵

三元组存储

十字链表法

其中列头链表M.chead:指向每一列的第一个结点

行头链表M.rhead:指向每一行的第一个结点

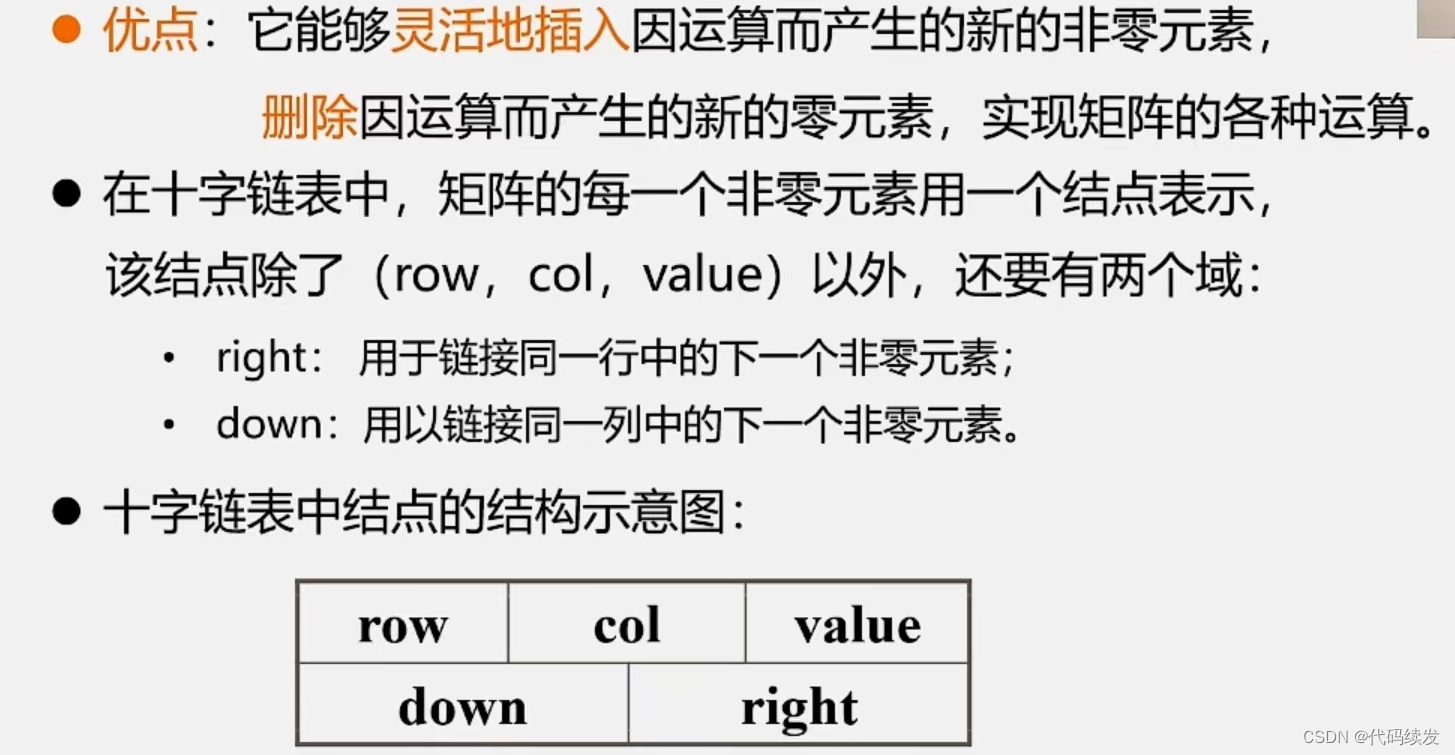
示例

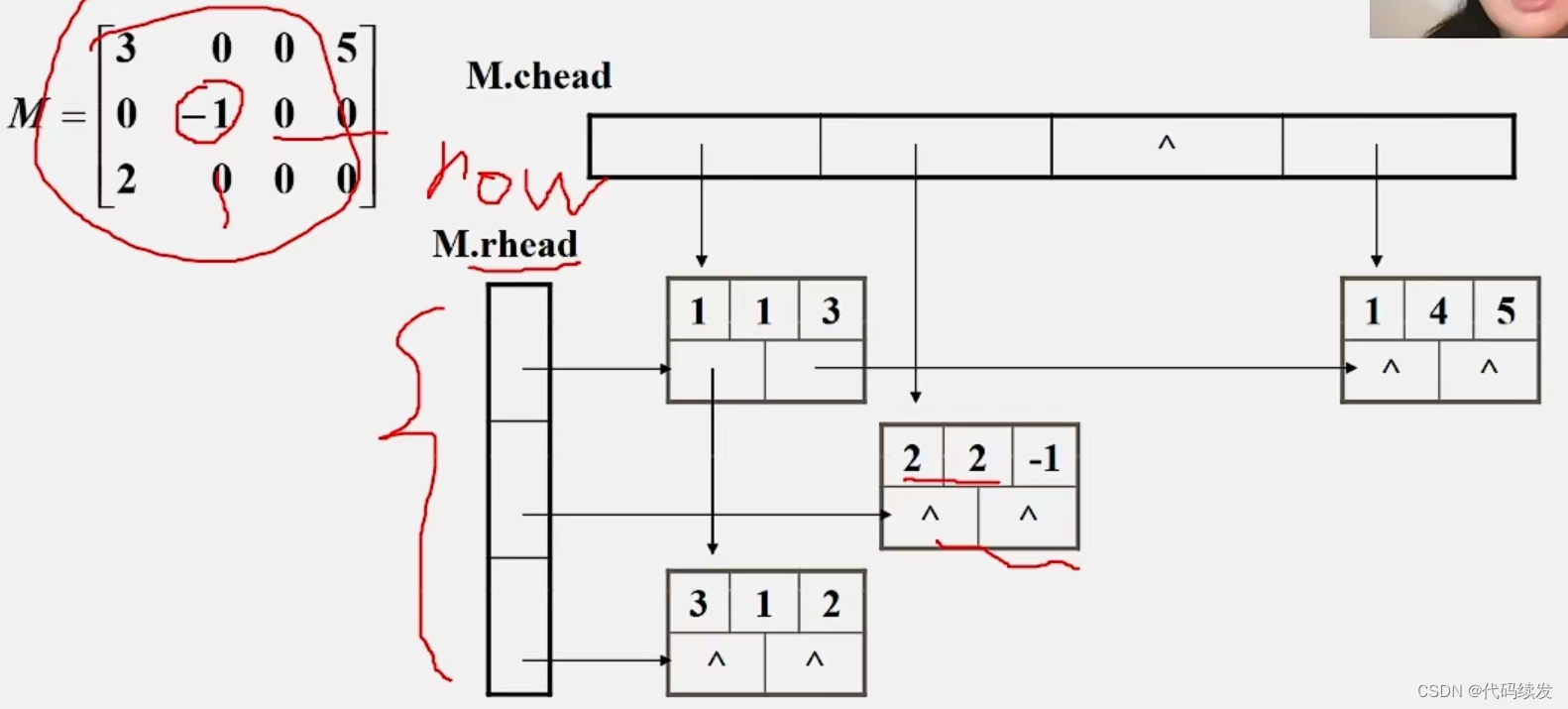
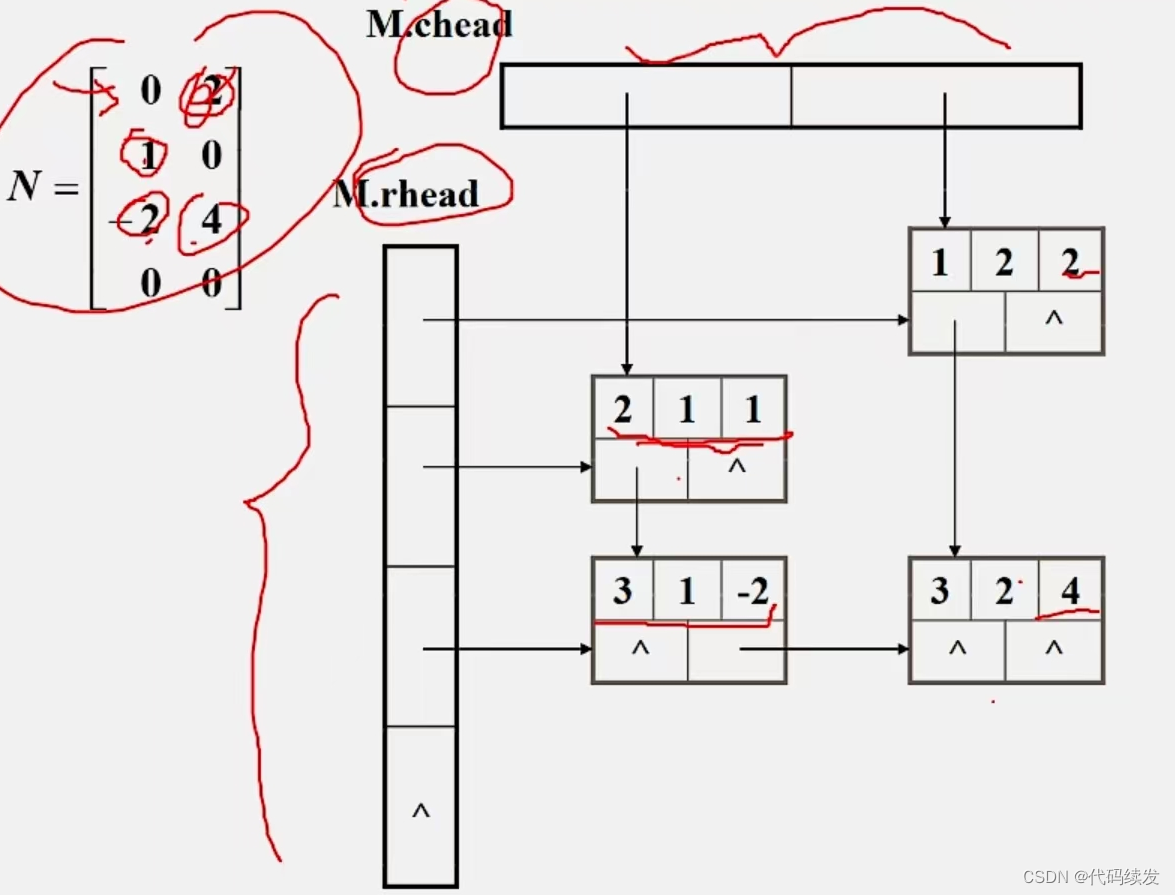
小结：

在计算aij压缩后，在压缩数组中的存储位置实际求解步骤：

1.求位置的元素个数：

以aij为例：若ij均是由1开始，个数=前i-1行所有元素个数+i行元素个数

前i-1行所有元素个数：

由等差数列公式求得，即（首项+末项）*项数/2求得

最关键看三个量：首项-开始行的元素个数1个  末项-第i-1行元素个数，此时每行元素个数与行数是一致的，为i-1个 项数-下标由1到i-1共i-1项  

所以前i-1行个数=（1+i-1)*(i-1)/2=i*(i-1)/2

i行元素个数：

即有多少列，j-i+1列(如a11第1行有1-1+1列)

总元素个数

aij共有i*(i-1)/2+j-i+1个元素

拓展用例：

那么如果ij均是由0开始，前i-1行的个数又如何求得呢？

看三个量：首项-开始行的元素个数1个  末项-第i-1行元素个数，此时每行元素个数比行数多1，所以为i个 项数-下标由0到i-1共i项  

所以前i-1行个数=（1+i)*(i)/2

i行个数=i行的列数=同样为j-i+1列

因此，此时aij共有（1+i)*(i)/2+j-i+1

结论：

一定要注意数组开始下标，不能盲目套用公式，我们是要求总个数，推理出来即可

2.由转储后在压缩数组B中的位置

以上我们已经求出总个数，那么最后一步就很好处理，直接根据B数组下标来存储

如果B由0开始存储：

那么aij存储状态为第1个存在下标为0的位置，以此类推，aij应存在下标为总个数-1的位置

如果B由1开始存储：

那么aij存储状态为第1个存在下标为1的位置，以此类推，aij应存在下标正好就是总个数的位置