（Java）心得：LeetCode——5.最长回文子串

news2024/11/18 14:37:03

一、原题

给你一个字符串 s，找到 s 中最长的回文子串。

如果字符串的反序与原始字符串相同，则该字符串称为回文字符串。

示例 1：

输入：s = "babad"
输出："bab"
解释："aba" 同样是符合题意的答案。

示例 2：

输入：s = "cbbd"
输出："bb"

二、心得

@官方，你管这叫中等难度题？(・∀・(・∀・(・∀・*)·····

我承认在上一篇我猖狂了，对不起（鞠躬90°）。简单一下说一说我的思路（思路不全，勿借鉴）：首先把字符串 s 进行 toCharArray() 方法，得到数组 c，执行如下代码：

for(int i = 1; i < s.length(); ++ i){
    for(int j = 1; j <= Math.min(i, s.length() - i - 1); j ++){
        if(c[i - j] == c[i + j]){
            return s.substring(i - j, i + j + 1);
        }
    }
}

我主要考虑的是以下情况（即，至少为 BAB 回文子串）：

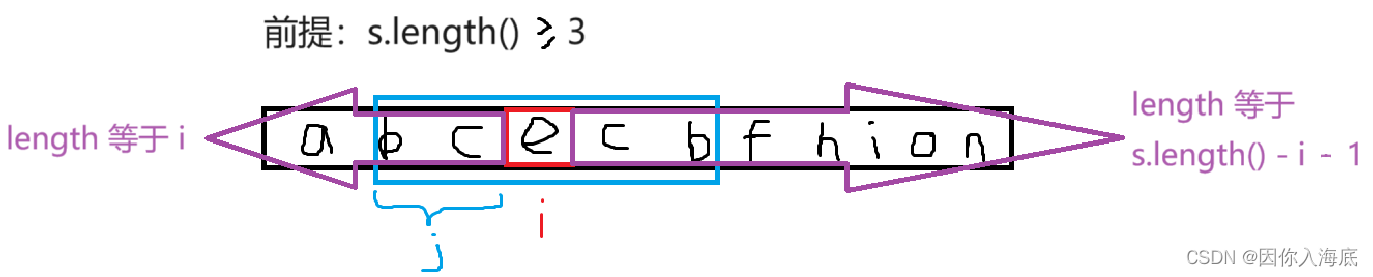
后来，我即使考虑了 s.length() 分别为1和2的情况等多种情况，但奈何测试时好多案例我都通不过，比如 s = "cccc“，s = "cccced"等，后来我发现需要考虑的情况太多，只好借鉴一下官方了（拿起我的小本本，乖乖坐好，(●'◡'●)）。

官解如下（动态规划）：

public class Solution {

    public String longestPalindrome(String s) {
        int len = s.length();
        if (len < 2) {
            return s;
        }

        int maxLen = 1;
        int begin = 0;
        // dp[i][j] 表示 s[i..j] 是否是回文串
        boolean[][] dp = new boolean[len][len];
        // 初始化：所有长度为 1 的子串都是回文串
        for (int i = 0; i < len; i++) {
            dp[i][i] = true;
        }

        char[] charArray = s.toCharArray();
        // 递推开始
        // 先枚举子串长度
        for (int L = 2; L <= len; L++) {
            // 枚举左边界，左边界的上限设置可以宽松一些
            for (int i = 0; i < len; i++) {
                // 由 L 和 i 可以确定右边界，即 j - i + 1 = L 得
                int j = L + i - 1;
                // 如果右边界越界，就可以退出当前循环
                if (j >= len) {
                    break;
                }

                if (charArray[i] != charArray[j]) {
                    dp[i][j] = false;
                } else {
                    if (j - i < 3) {
                        dp[i][j] = true;
                    } else {
                        dp[i][j] = dp[i + 1][j - 1];
                    }
                }

                // 只要 dp[i][L] == true 成立，就表示子串 s[i..L] 是回文，此时记录回文长度和起始位置
                if (dp[i][j] && j - i + 1 > maxLen) {
                    maxLen = j - i + 1;
                    begin = i;
                }
            }
        }
        return s.substring(begin, begin + maxLen);
    }
}

首先，官解的核心思想为（前提 s 的长度大于2）：

P(i, j) = P(i + 1, j − 1) ∧ (Si == Sj)

P(i, j) 表示字符串 s 的第 i 到 j 个字母组成的串

只要 P(i + 1, j −1) 和 Si == Sj 都满足，则 P(i, j) 一定为回文子串。这样解决了我只能考虑长度为奇数的回味子串的问题，即奇偶长度的回文都考虑了。

后只需确定动态规划的边界条件：

P(i, i + 1) = (Si == S(i+1))

只要存在相邻的相同的字母，那么它们一定是回文。

对于为什么要用 boolean[][] dp = new boolean[len][len];，如表所示：

以s="babad"为例，假设取最大回文为"bab"
	dp[][0]	dp[][1]	dp[][2]	dp[][3]	dp[][4]
dp[0][]	(b,b)	(b,a)	(b,b)	(b,a)	(b,d)
dp[1][]	(a,b)	(a,a)	(a,b)	(a,a)	(a,d)
dp[2][]	(b,b)	(b,a)	(b,b)	(b,a)	(a,d)
dp[3][]	(a,b)	(a,a)	(a,b)	(a,a)	(b,b)
dp[4][]	(d,b)	(d,a)	(d,b)	(d,a)	(d,d)