【高阶数据结构】图--最短路径问题

news2024/10/6 6:50:35

图--最短路径问题

  • 一、单源最短路径--Dijkstra算法
    • 1、简介
    • 2、解析
    • 3、代码
    • 4、测试用例
    • 5、打印最小路径代码和测试
    • 6、缺陷：不能使用负路径
  • 二、单源最短路径--Bellman-Ford算法
    • 1、简介
    • 2、解析
      • （1）详情
        • i、负权问题：一个点只跑一趟找最短路径（问题大大的）
        • ii、解决负权问题：每个点在更新完最短路径后继续暴力再继续遍历更新最短路径
      • （2）优化
        • i、优化策略1：使用bool标记位跳出循环，后面循环不用跑
        • ii、优化策略2：使用SPFA算法优化（队列）（未做出）
    • 3、代码
    • 4、测试用例及测试结果
    • 5、负权回路问题
      • （1）问题描述和解析
      • （2）出现负权问题的代码用例及测试结果
  • 三、多源最短路径--Floyd-Warshall算法
    • （1）简介
    • （2）详细解析（用图）
    • （3）代码
    • （4）运行用例及测试结果

一、单源最短路径–Dijkstra算法

1、简介

单源最短路径问题：给定一个图G = ( V ， E ) G=(V，E)G=(V，E)，求源结点s ∈ V s∈Vs∈V到图中每个结点v ∈ V v∈Vv∈V的最短路径。Dijkstra算法就适用于解决带权重的有向图上的单源最短路径问题，同时算法要求图中所有边的权重非负。一般在求解最短路径的时候都是已知一个起点和一个终点，所以使用Dijkstra算法求解过后也就得到了所需起点到终点的最短路径。
针对一个带权有向图G，将所有结点分为两组S和Q，S是已经确定最短路径的结点集合，在初始时为空（初始时就可以将源节点s放入，毕竟源节点到自己的代价是0），Q 为其余未确定最短路径的结点集合，每次从Q 中找出一个起点到该结点代价最小的结点u ，将u 从Q 中移出，并放入S 中，对u 的每一个相邻结点v 进行松弛操作。松弛即对每一个相邻结点v ，判断源节点s到结点u的代价与u 到v 的代价之和是否比原来s 到v 的代价更小，若代价比原来小则要将s 到v 的代价更新为s 到u 与u 到v 的代价之和，否则维持原样。如此一直循环直至集合Q 为空，即所有节点都已经查找过一遍并确定了最短路径，至于一些起点到达不了的结点在算法循环后其代价仍为初始设定的值，不发生变化。Dijkstra算法每次都是选择V-S中最小的路径节点来进行更新，并加入S中，所以该算法使用的是贪心策略。
Dijkstra算法存在的问题是不支持图中带负权路径，如果带有负权路径，则可能会找不到一些路径的最短路径。

2、解析

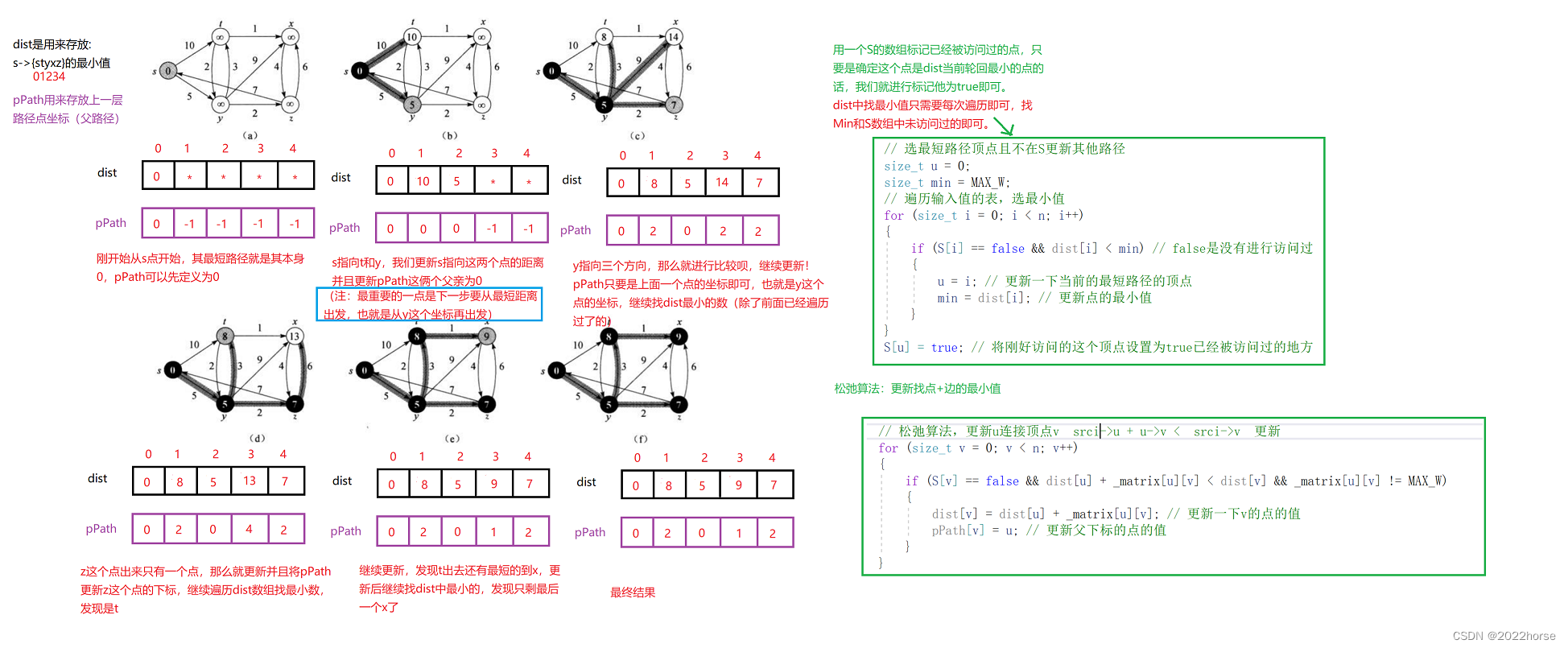
在这里插入图片描述

3、代码

		// Dijkstrala算法
		// dist是用来存放最小值的表的
		// pPath是用来存放父亲下标的
		void Dijkstra(const V& src, std::vector<W>& dist, std::vector<int>& pPath)
		{
			size_t srci = GetIndex(src);
			size_t n = _vertex.size();
			// 初始化dist表和pPath表
			dist.resize(n, MAX_W);
			pPath.resize(n, -1);
			dist[srci] = 0; // 当前的第一个位置的距离为0
			pPath[srci] = srci; // 这个可有可无
			// 来一个S为存放加入到集合中的已经确定了的点
			std::vector<bool> S(n, false);
			for (size_t i = 0; i < n; i++) // 遍历n次--n个顶点
			{
				// 选最短路径顶点且不在S更新其他路径
				size_t u = 0;
				size_t min = MAX_W;
				// 遍历输入值的表，选最小值
				for (size_t i = 0; i < n; i++)
				{
					if (S[i] == false && dist[i] < min) // false是没有进行访问过
					{
						u = i; // 更新一下当前的最短路径的顶点
						min = dist[i]; // 更新点的最小值
					}
				}
				S[u] = true; // 将刚好访问的这个顶点设置为true已经被访问过的地方
				// 松弛算法，更新u连接顶点v  srci->u + u->v <  srci->v  更新
				for (size_t v = 0; v < n; v++)
				{
					if (S[v] == false && dist[u] + _matrix[u][v] < dist[v] && _matrix[u][v] != MAX_W)
					{
						dist[v] = dist[u] + _matrix[u][v]; // 更新一下v的点的值
						pPath[v] = u; // 更新父下标的点的值
					}
				}
			}
		}

4、测试用例

	void TestGraphDijkstra()
	{
		const char* str = "syztx";
		Graph<char, int, INT_MAX, true> g(str, strlen(str));
		g.AddEdge('s', 't', 10);
		g.AddEdge('s', 'y', 5);
		g.AddEdge('y', 't', 3);
		g.AddEdge('y', 'x', 9);
		g.AddEdge('y', 'z', 2);
		g.AddEdge('z', 's', 7);
		g.AddEdge('z', 'x', 6);
		g.AddEdge('t', 'y', 2);
		g.AddEdge('t', 'x', 1);
		g.AddEdge('x', 'z', 4);
		std::vector<int> dist;
		std::vector<int> parentPath;
		g.Dijkstra('s', dist, parentPath);
		g.PrinrtShotPath('s', dist, parentPath);
	}

5、打印最小路径代码和测试

		void PrinrtShotPath(const V& src, const std::vector<W>& dist, const std::vector<int>& parentPath)
		{
			size_t N = _vertex.size();
			size_t srci = GetIndex(src);
			for (size_t i = 0; i < N; ++i)
			{
				if (i == srci)
					continue;

				std::vector<int> path;
				int parenti = i;
				while (parenti != srci)
				{
					path.push_back(parenti); // 先把自己存进去
					parenti = parentPath[parenti]; // 往父亲去跳
				}
				path.push_back(srci); // 最后存初始位置
				reverse(path.begin(), path.end()); // 逆置一下
				for (auto pos : path)
				{
					std::cout << _vertex[pos] << "->";
				}
				std::cout << dist[i] << std::endl;
			}
		}

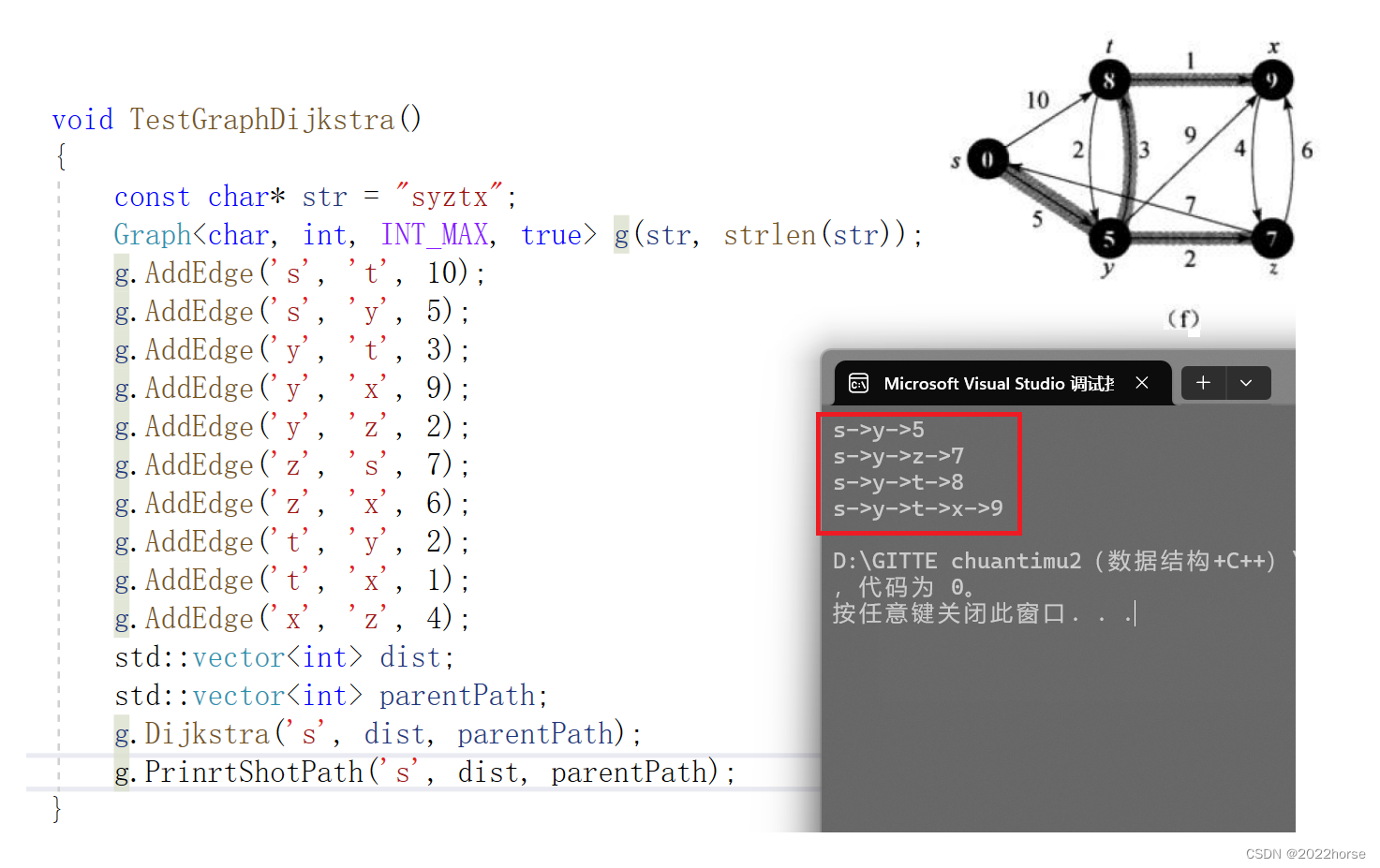
在这里插入图片描述

6、缺陷：不能使用负路径

const char* str = "sytx";
		 Graph<char, int, INT_MAX, true> g(str, strlen(str));
		 g.AddEdge('s', 't', 10);
		 g.AddEdge('s', 'y', 5);
		 g.AddEdge('t', 'y', -7);
		 g.AddEdge('y', 'x', 3);
		 std::vector<int> dist;
		 std::vector<int> parentPath;
		 g.Dijkstra('s', dist, parentPath);
		 g.PrinrtShotPath('s', dist, parentPath);

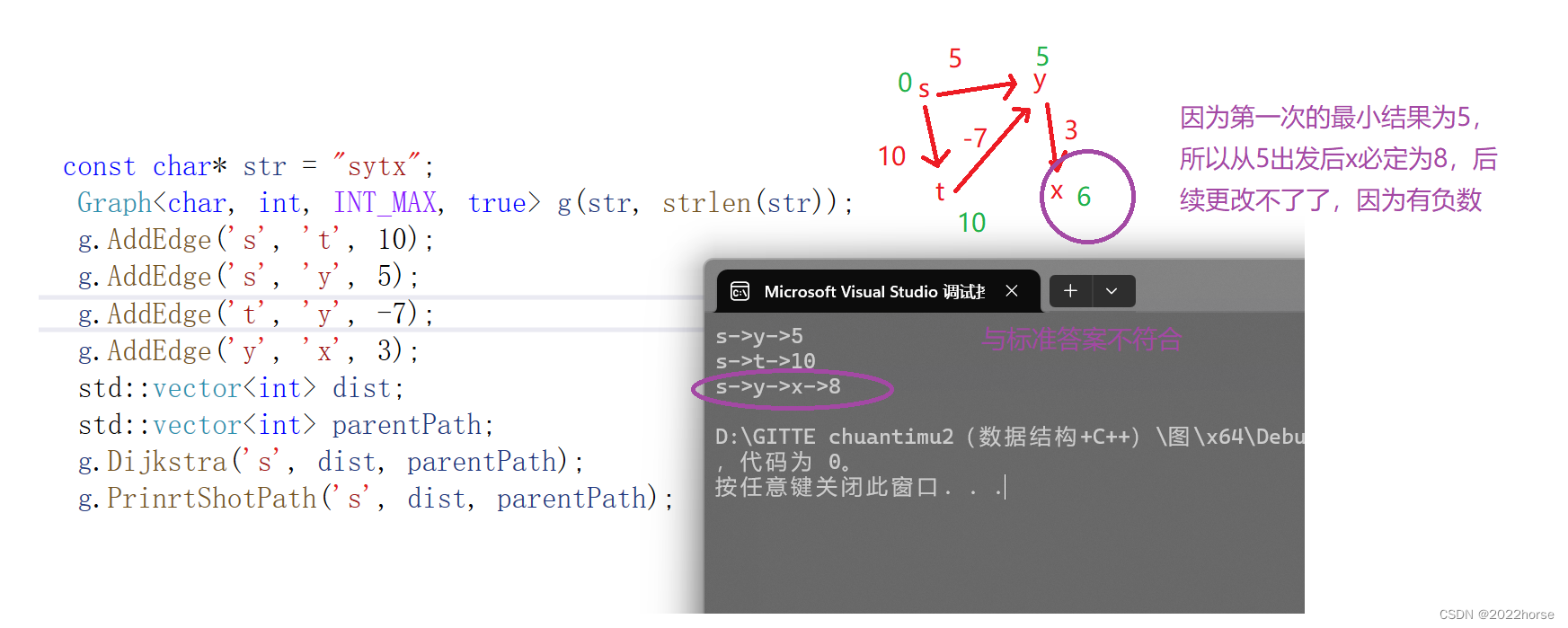
在这里插入图片描述

二、单源最短路径–Bellman-Ford算法

1、简介

Dijkstra算法只能用来解决正权图的单源最短路径问题，但有些题目会出现负权图。这时这个算法就不能帮助我们解决问题了，而bellman—ford算法可以解决负权图的单源最短路径问题。它的优点是可以解决有负权边的单源最短路径问题，而且可以用来判断是否有负权回路。它也有明显的缺点，它的时间复杂度 O(N*E) (N是点数，E是边数)普遍是要高于Dijkstra算法O(N²)的。像这里如果我们使用邻接矩阵实现，那么遍历所有边的数量的时间复杂度就是O(N^3)，这里也可以看出来Bellman-Ford就是一种暴力求解更新。

2、解析

（1）详情

i、负权问题：一个点只跑一趟找最短路径（问题大大的）

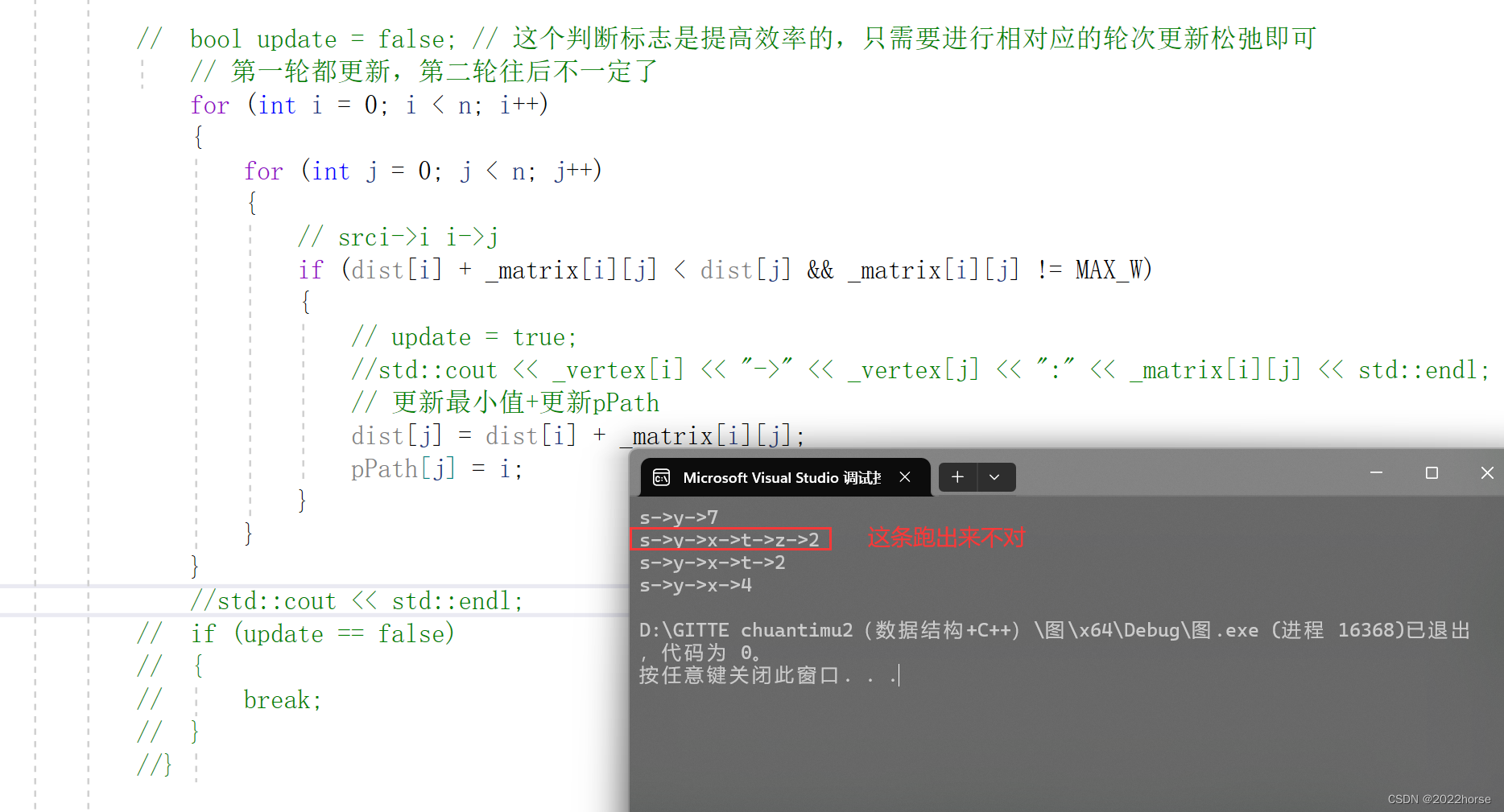
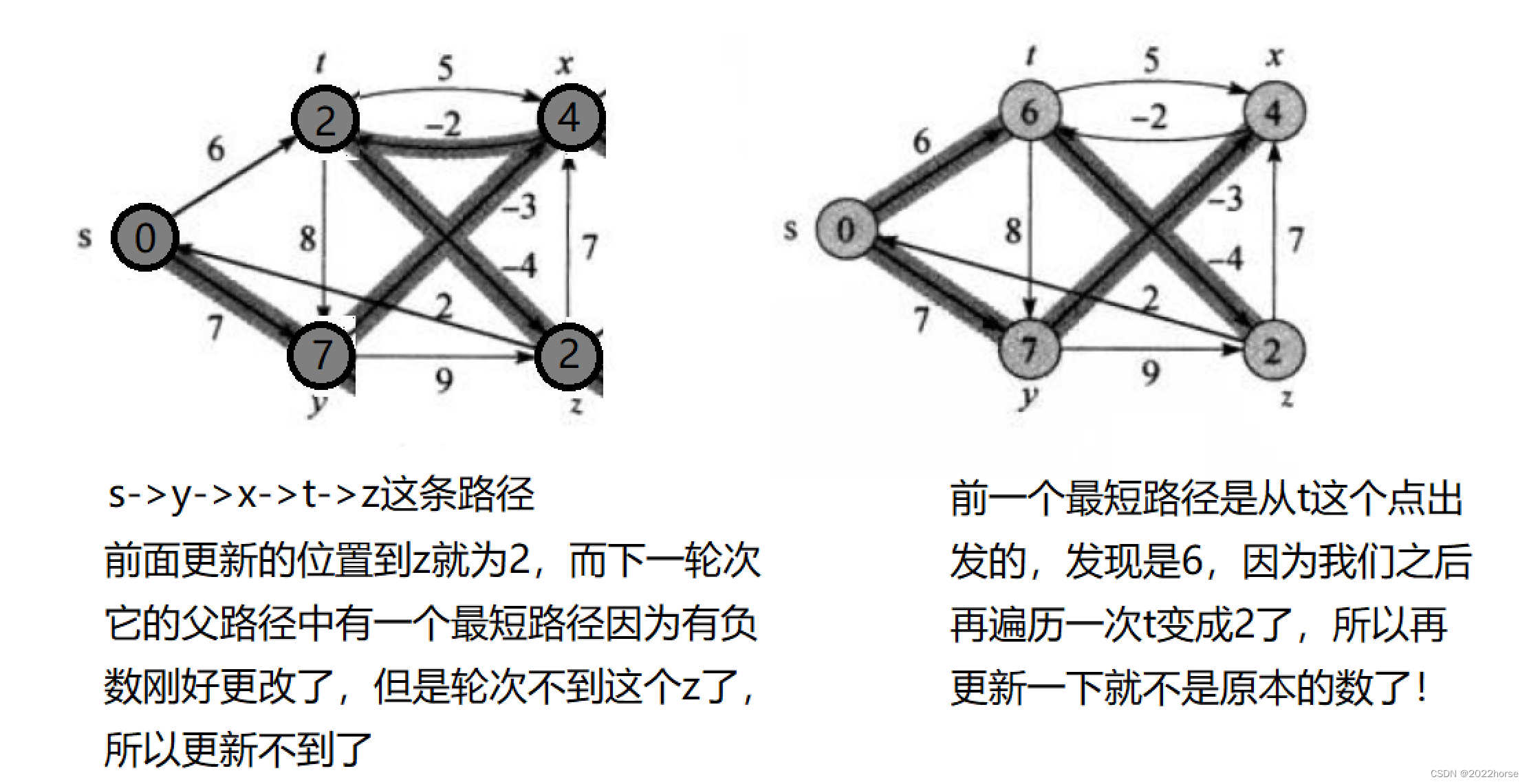
在这里插入图片描述

在这里插入图片描述

ii、解决负权问题：每个点在更新完最短路径后继续暴力再继续遍历更新最短路径

原因还是因为负权路径的问题，当我们更新完一趟的最短路径后发现其父亲节点是个负数，刚好通过这条路，而我们前面更新的最短路径不是从这条路走的，那么就需要继续更新前面这个父亲结点的最短路径为负数，使得这个最短路径更新成更小的值，那么一切就说通了，我们就需要继续更新呗，那么就继续更新n次，每个点继续遍历n次。

// 进行n轮循环，原因是因为防止因为某一轮循环后值会产生更改导致的结果不正确
			// 所以每次进行点的询问松弛，使得后续的路径更新成更短路径
			for (int k = 0; k < n; k++)
			{
				std::cout << "第" << k << "轮次" << std::endl;
			}

我们跟着最终结果来看：
在这里插入图片描述

（2）优化

i、优化策略1：使用bool标记位跳出循环，后面循环不用跑

因为第一个轮次是将所有的路都跑一遍（初始跑一遍），第二个轮次还是从头到尾的跑一遍，这回轮次是找负数重新更新一下最短路径，而假如说路径的负数并不多的时候，两个轮次就能全部跑完了，并不需要后面冗余的n-3个轮次，所以我们给个标志位，从第i个轮次发现根本不会更改路劲的情况下我们直接退出，不需要执行下一个轮回的操作。
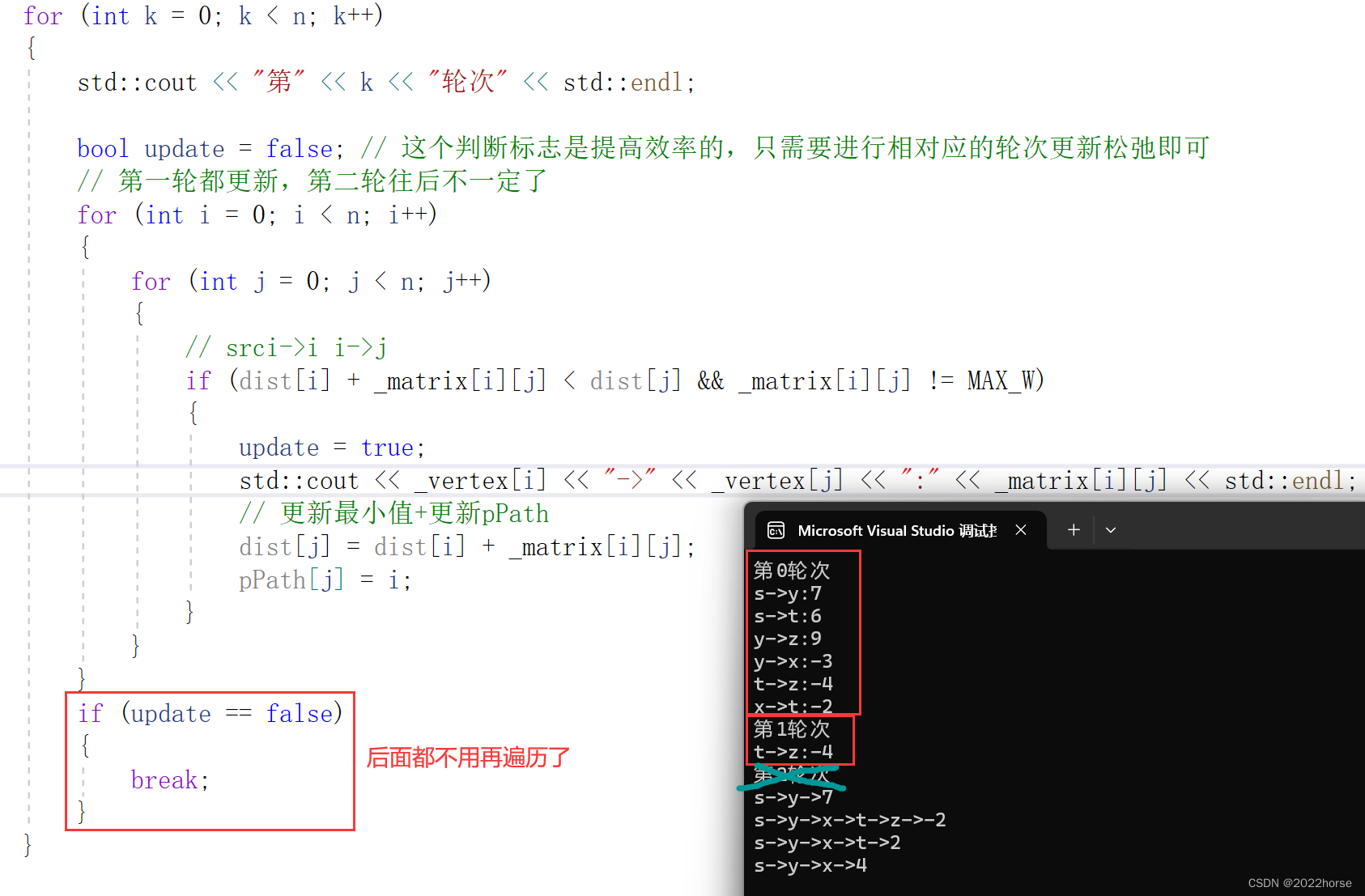
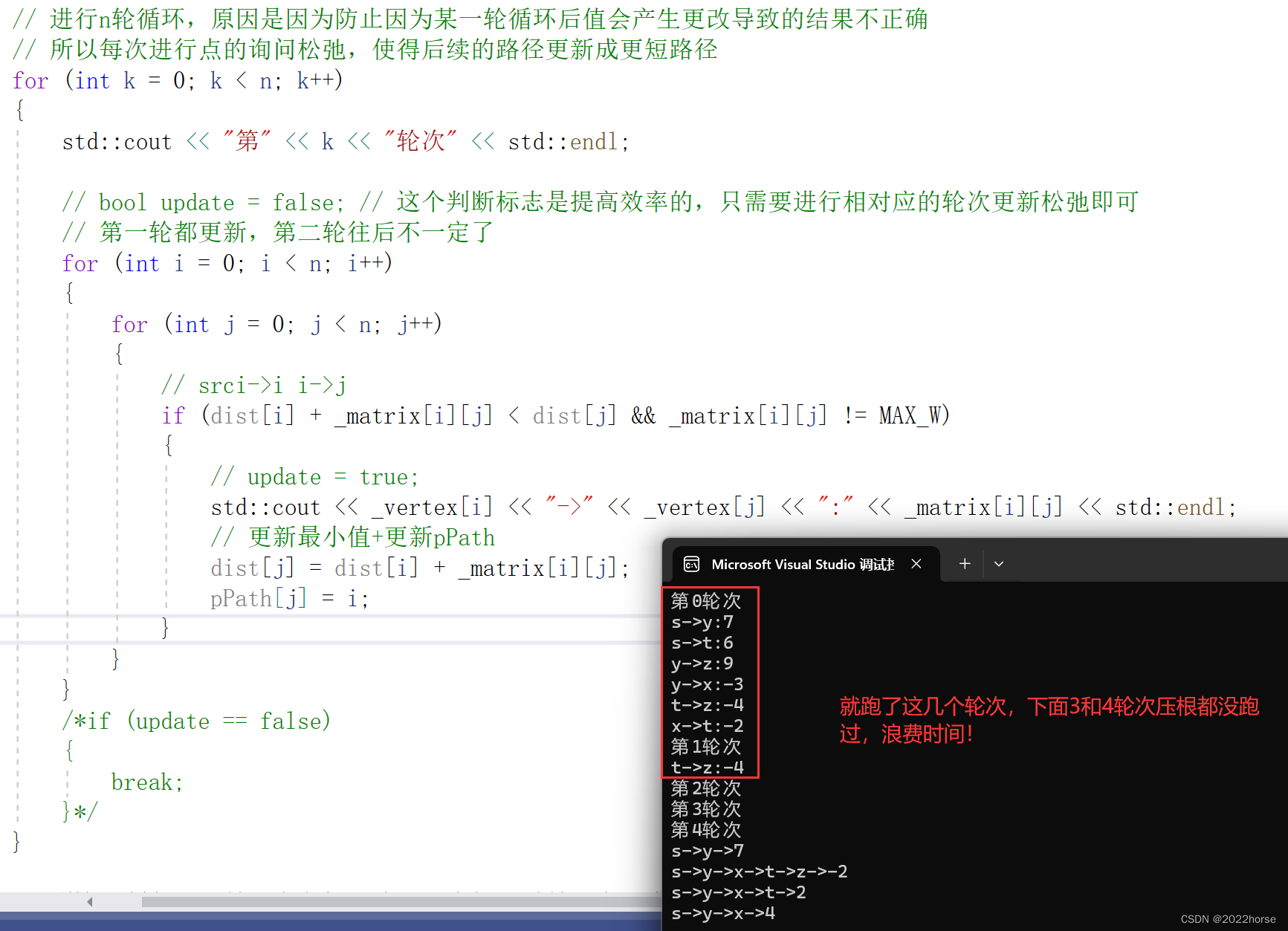
在这里插入图片描述

在这里插入图片描述

ii、优化策略2：使用SPFA算法优化（队列）（未做出）

在这里插入图片描述

革命尚未成功，同志仍需努力…

3、代码

		// 贝尔曼福特算法
		// 时间复杂度--O(N^3) 空间复杂度--O(N)
		bool BellmanFord(const V& src, std::vector<W>& dist, std::vector<int>& pPath)
		{
			size_t n = _vertex.size();
			size_t srci = GetIndex(src);

			// vector<W> dist,记录srci-其他顶点最短路径权值数组
			dist.resize(n, MAX_W);
			
			// vector<int> pPath 记录srci-其他顶点最短路径父顶点数组
			pPath.resize(n, -1);
			// 先更新srci->srci为最小值
			dist[srci] = W();
			// 进行n轮循环，原因是因为防止因为某一轮循环后值会产生更改导致的结果不正确
			// 所以每次进行点的询问松弛，使得后续的路径更新成更短路径
			for (int k = 0; k < n; k++)
			{
				bool update = false; // 这个判断标志是提高效率的，只需要进行相对应的轮次更新松弛即可
				// 第一轮都更新，第二轮往后不一定了
				for (int i = 0; i < n; i++)
				{
					for (int j = 0; j < n; j++)
					{
						// srci->i i->j
						if (dist[i] + _matrix[i][j] < dist[j] && _matrix[i][j] != MAX_W)
						{
							// 更新最小值+更新pPath
							dist[j] = dist[i] + _matrix[i][j];
							pPath[j] = i;
							update = true;
						}
					}
				}
				if (update == false)
				{
					break;
				}
			}

			// 到这里判断一下是否有负权回路，因为加入说是三个形成一个带有负值回路，那么每一轮都会将值更新
			// 这就是负权回路问题，遇到这个负权回路问题也解决不了，那么就返回false即可
			for (int i = 0; i < n; i++)
			{
				for (int j = 0; j < n; j++)
				{
					// srci->i i->j
					if (dist[i] + _matrix[i][j] < dist[j] && _matrix[i][j] != MAX_W)
					{
						return false;
					}
				}
			}
			return true;
		}

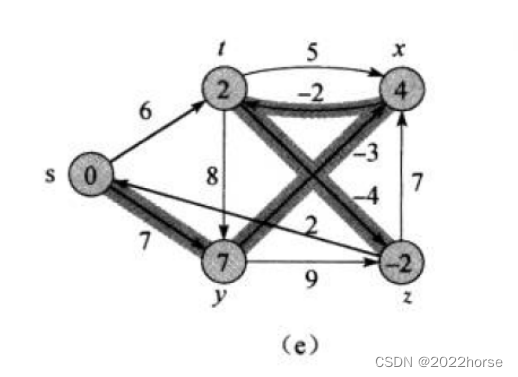
4、测试用例及测试结果

	void TestGraphBellmanFord()
	{
		const char* str = "syztx";
		Graph<char, int, INT_MAX, true> g(str, strlen(str));
		g.AddEdge('s', 't', 6);
		g.AddEdge('s', 'y', 7);
		g.AddEdge('y', 'z', 9);
		g.AddEdge('y', 'x', -3);
		g.AddEdge('z', 's', 2);
		g.AddEdge('z', 'x', 7);
		g.AddEdge('t', 'x', 5);
		g.AddEdge('t', 'y', 8);
		g.AddEdge('t', 'z', -4);
		g.AddEdge('x', 't', -2);
		std::vector<int> dist;
		std::vector<int> parentPath;
		if (g.BellmanFord('s', dist, parentPath))
		{
			g.PrinrtShotPath('s', dist, parentPath);
		}
		else
		{
			std::cout << "存在负权回路" << std::endl;
		}
	}

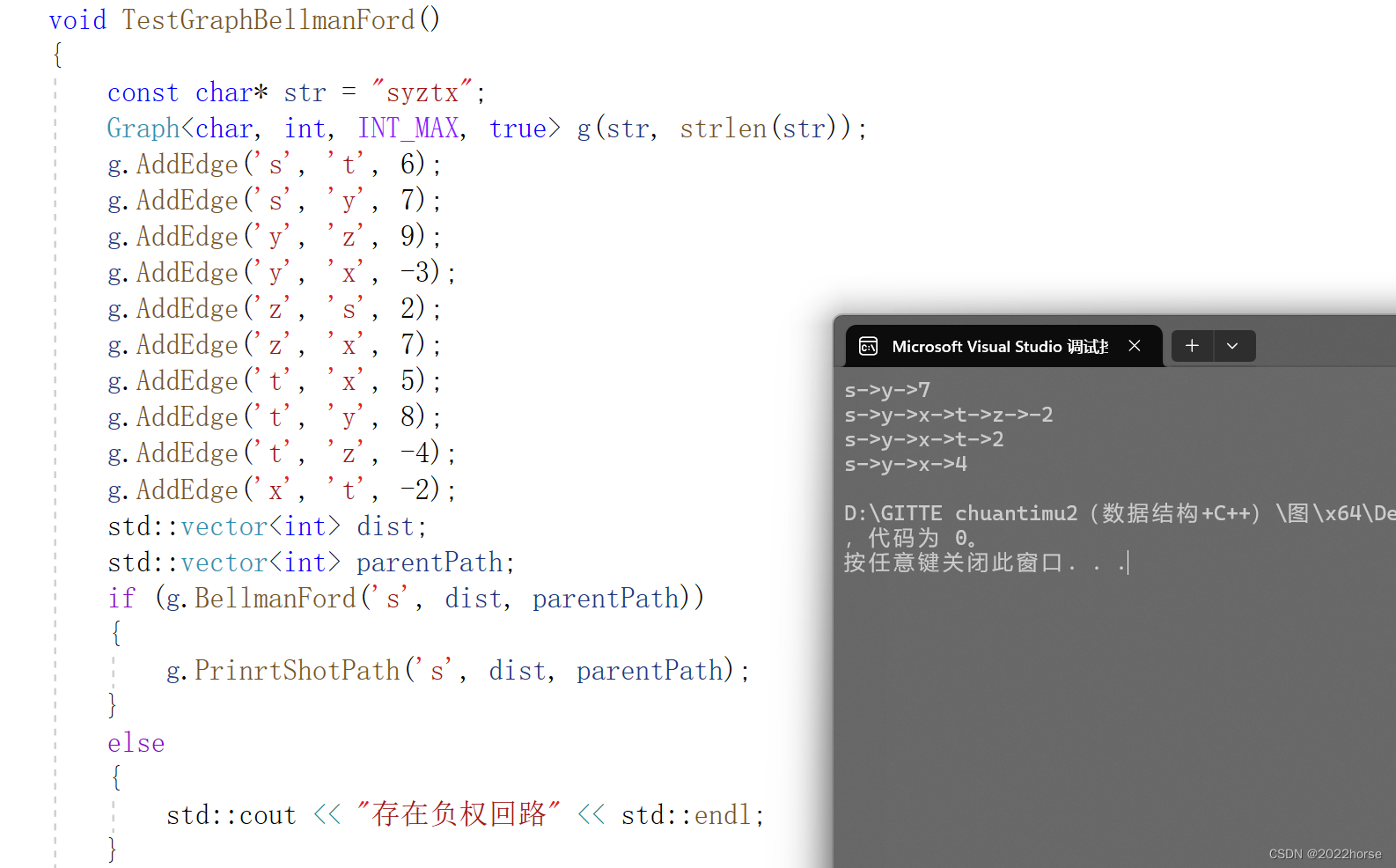
在这里插入图片描述

在这里插入图片描述

5、负权回路问题

（1）问题描述和解析

我们出现负权回路的问题，大概率是出现一个环，这个环中刚好有一个或多个边的权值是负数，如下图所示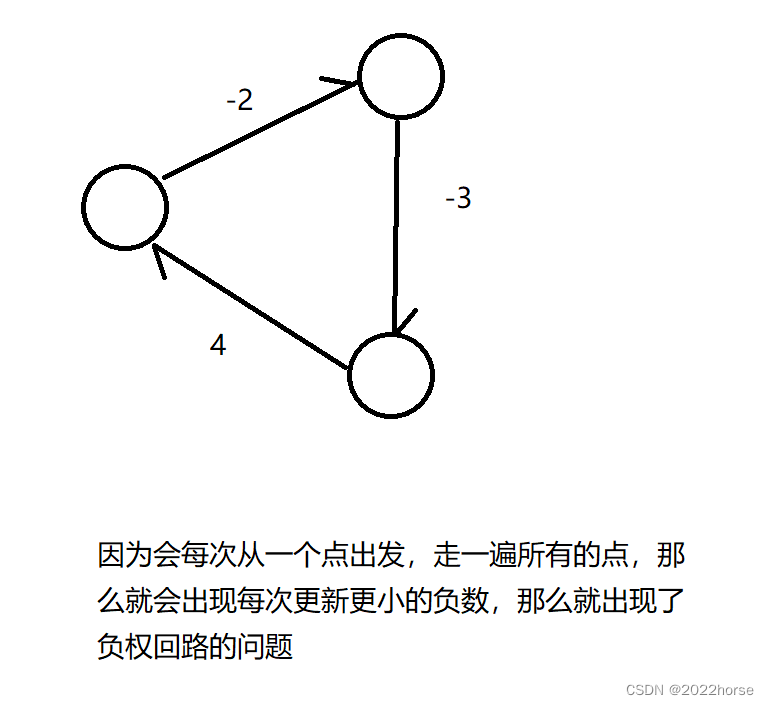：在这里插入图片描述
那么我们想一想是否这种情况能不能避免或者是有什么算法避免？实际上一旦遇到这个问题就完蛋了，没有任何算法能够规避，直接说出现回路问题，不管了！

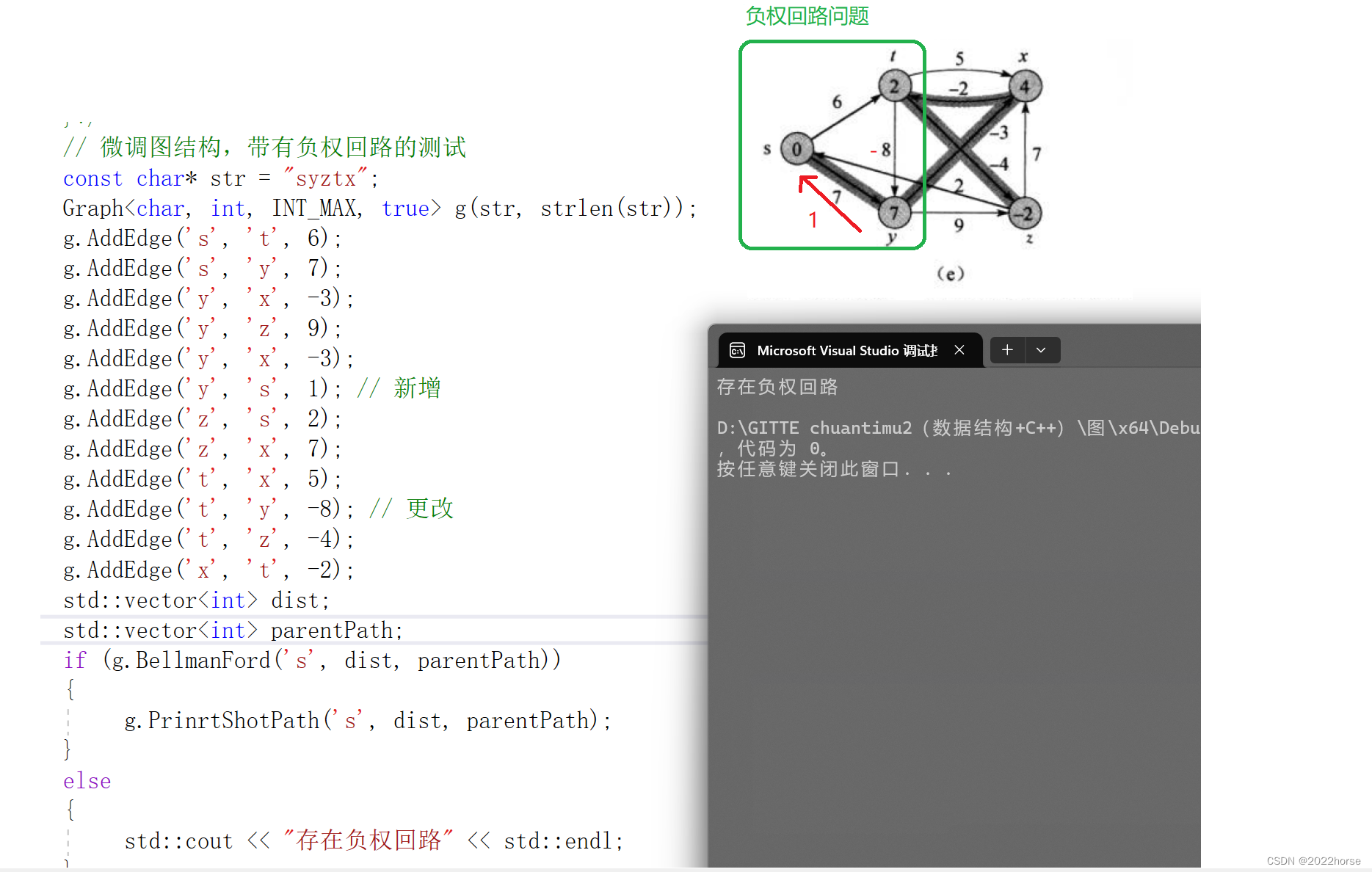
（2）出现负权问题的代码用例及测试结果

// 微调图结构，带有负权回路的测试
		const char* str = "syztx";
		Graph<char, int, INT_MAX, true> g(str, strlen(str));
		g.AddEdge('s', 't', 6);
		g.AddEdge('s', 'y', 7);
		g.AddEdge('y', 'x', -3);
		g.AddEdge('y', 'z', 9);
		g.AddEdge('y', 'x', -3);
		g.AddEdge('y', 's', 1); // 新增
		g.AddEdge('z', 's', 2);
		g.AddEdge('z', 'x', 7);
		g.AddEdge('t', 'x', 5);
		g.AddEdge('t', 'y', -8); // 更改
		g.AddEdge('t', 'z', -4);
		g.AddEdge('x', 't', -2);
		std::vector<int> dist;
		std::vector<int> parentPath;
		if (g.BellmanFord('s', dist, parentPath))
		{
			 g.PrinrtShotPath('s', dist, parentPath);
		}
		else
		{
			 std::cout << "存在负权回路" << std::endl;
		}

在这里插入图片描述

三、多源最短路径–Floyd-Warshall算法

（1）简介

Floyd-Warshall算法是解决任意两点间的最短路径的一种算法。
Floyd算法考虑的是一条最短路径的中间节点，即简单路径p={v1,v2,…,vn}上除v1和vn的任意节点。
设k是p的一个中间节点，那么从i到j的最短路径p就被分成i到k和k到j的两段最短路径p1，p2。p1是从i到k且中间节点属于{1，2，…，k-1}取得的一条最短路径。p2是从k到j且中间节点属于{1，2，…，k-1}取得的一条最短路径。

（2）详细解析（用图）

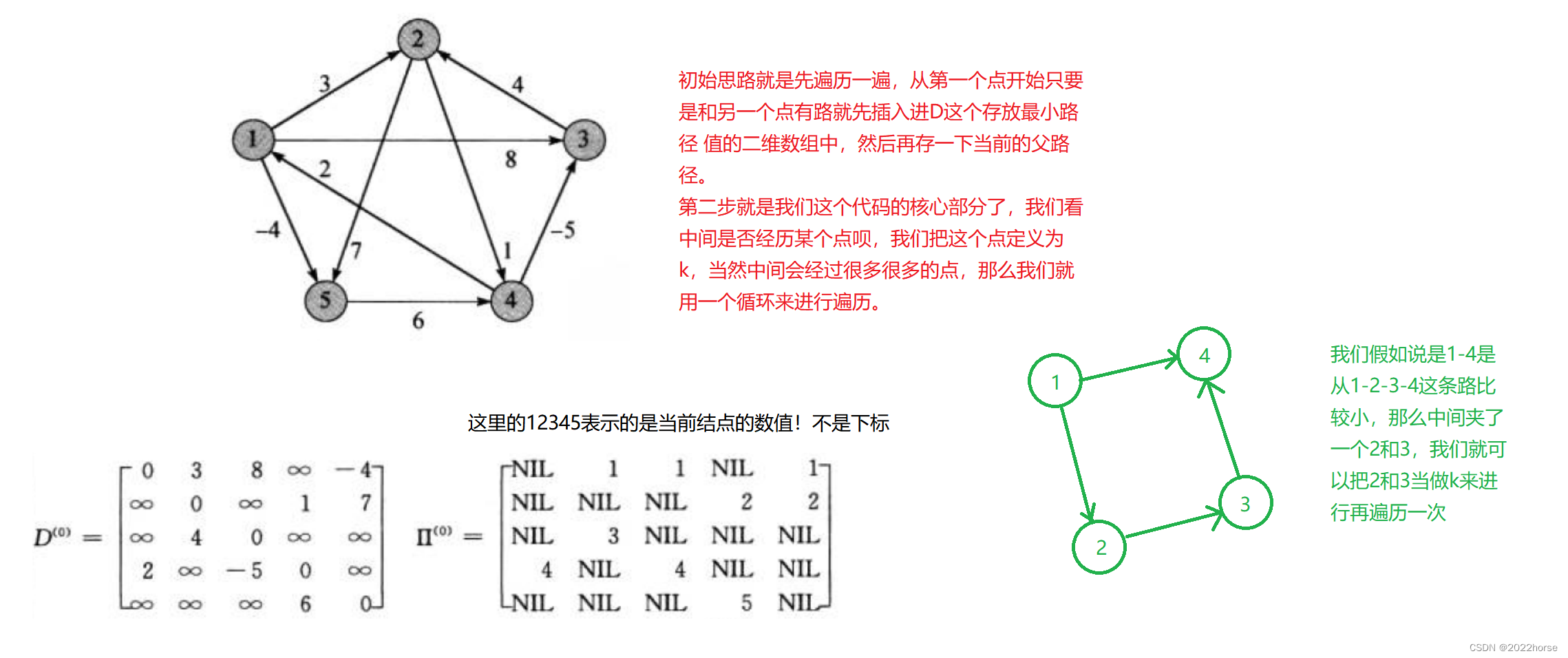
在这里插入图片描述

除了时间复杂度太高几乎没别的缺点了，它允许负权路径的存在。

（3）代码

		// FloydWarshall算法--多源最短路径的表示
		// vvDist是二维用来存放最短路径的表格
		// vvpPath是二维用来存放父路径的
		void FloydWarshall(std::vector<std::vector<W>>& vvDist, std::vector<std::vector<int>>& vvpPath)
		{
			size_t n = _vertex.size();
			vvDist.resize(n); // 有多少行
			vvpPath.resize(n);

			// 初始化权值和路径矩阵
			for (size_t i = 0; i < n; ++i)
			{
				vvDist[i].resize(n, MAX_W); // 每一行每一列
				vvpPath[i].resize(n, -1);
			}

			// 先将每条边更新一下
			for (size_t i = 0; i < n; i++)
			{
				for (size_t j = 0; j < n; j++)
				{
					if (_matrix[i][j] != MAX_W) // 当i->j点是有路的时候
					{
						vvDist[i][j] = _matrix[i][j];
						vvpPath[i][j] = i; // 刚好是j的前一个路径就是i
					}
					if (i == j) // 对角线
					{
						vvDist[i][j] = W(); // 缺省的默认值
					}
				}
			}

			// 算法核心：1、中间有k的时候:i->{n个数(包含k)}->j   dist[i][k] + dist[k][j] 与 dist[i][j]比较
			// 2、中间没有k的时候，那么就是i->j，也就是和上面的情况一样了，压根都不需要管了
			for (size_t k = 0; k < n/*这里k的值是n的原因在于ij也可以都包进来的*/; k++)
			{
				for (size_t i = 0; i < n; i++)
				{
					for (size_t j = 0; j < n; j++)
					{
						// i到k有路径 k到j有路径
						if (vvDist[i][k] + vvDist[k][j] < vvDist[i][j] && 
								vvDist[i][k] != MAX_W && vvDist[k][j] != MAX_W)
						{
							vvDist[i][j] = vvDist[i][k] + vvDist[k][j];
							// 找跟j相连的上一个邻接顶点
							// 如果k->j 直接相连，上一个点就k，vvpPath[k][j]存就是k
							// 如果k->j 没有直接相连，k->...->x->j，vvpPath[k][j]存就是x
							vvpPath[i][j] = vvpPath[k][j]; // 动态规划--j的前面一个元素k咯
						}
					}
				}
			}

			// 打印权值和路径矩阵观察数据
			for (size_t i = 0; i < n; ++i)
			{
				for (size_t j = 0; j < n; ++j)
				{
					if (vvDist[i][j] == MAX_W)
					{
						printf("%3c", '*');
					}
					else
					{
						printf("%3d", vvDist[i][j]);
					}
				}
				std::cout << std::endl;
			}
			std::cout << std::endl;
			// 打印父路径
			for (size_t i = 0; i < n; ++i)
			{
				for (size_t j = 0; j < n; ++j)
				{
					printf("%3d", vvpPath[i][j]); // 这里打印的是下标
				}
				std::cout << std::endl;
			}
			std::cout << "=================================" << std::endl;
		}

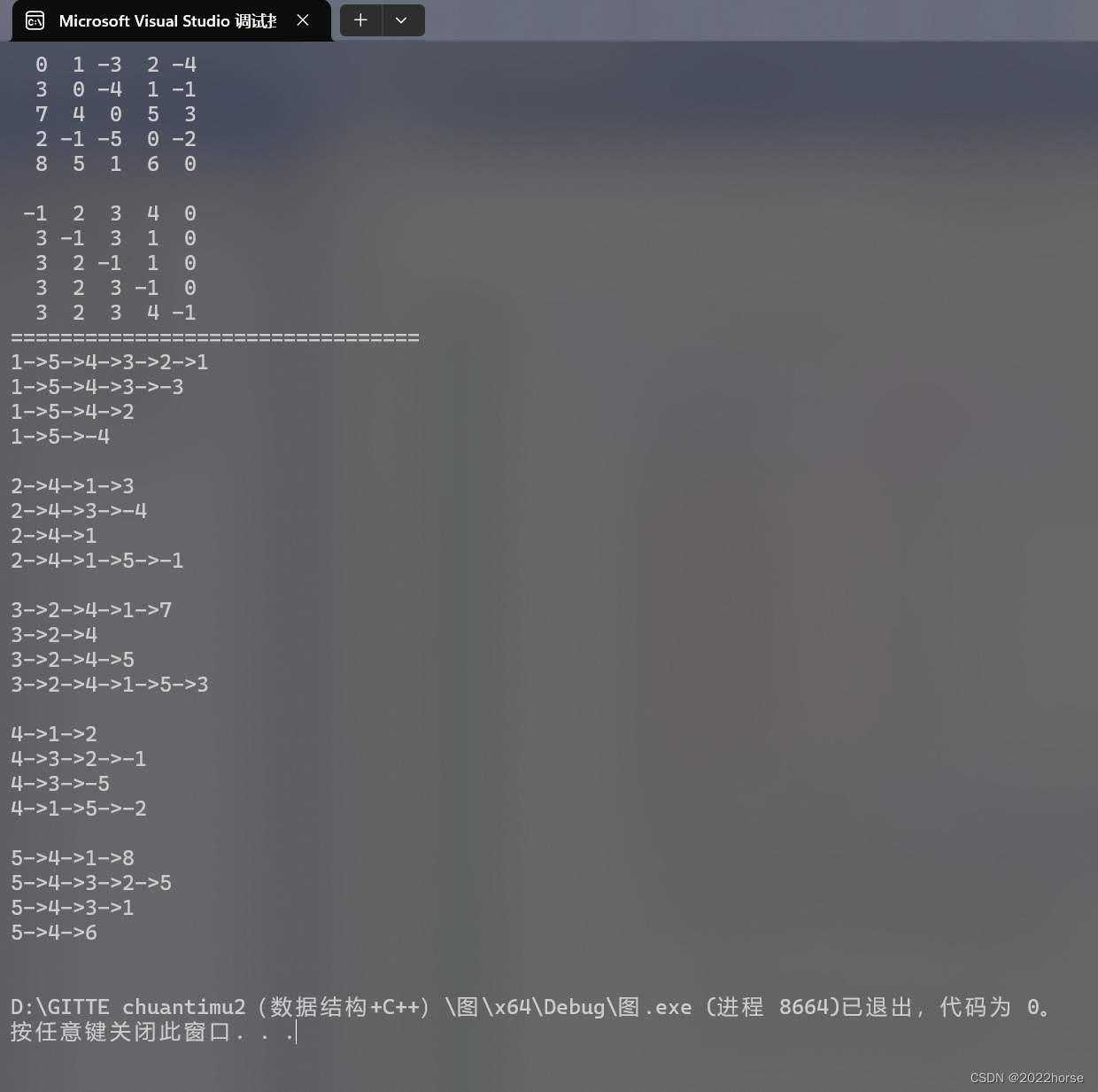
（4）运行用例及测试结果

	void TestFloydWarShall()
	{
		const char* str = "12345";
		Graph<char, int, INT_MAX, true> g(str, strlen(str));
		g.AddEdge('1', '2', 3);
		g.AddEdge('1', '3', 8);
		g.AddEdge('1', '5', -4);
		g.AddEdge('2', '4', 1);
		g.AddEdge('2', '5', 7);
		g.AddEdge('3', '2', 4);
		g.AddEdge('4', '1', 2);
		g.AddEdge('4', '3', -5);
		g.AddEdge('5', '4', 6);
		std::vector<std::vector<int>> vvDist;
		std::vector<std::vector<int>> vvParentPath;
		g.FloydWarshall(vvDist, vvParentPath);
		// 打印任意两点之间的最短路径
		for (size_t i = 0; i < strlen(str); ++i)
		{
			g.PrinrtShotPath(str[i], vvDist[i], vvParentPath[i]);
			std::cout << std::endl;
		}
	}

在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1664049.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

整除C++

整除C++

题目&#xff1a; 思路&#xff1a; 循环遍历7(可以被 7 整除的正整数最小为7)~n&#xff0c;如果i%70&#xff0c;就说明i可以被7整除. 代码&#xff1a; #include<iostream> using namespace std; int n;//一个正整数 int main(){scanf("%d",&n);//输入…
阅读更多...
Vue.js【路由】

Vue.js【路由】

初识路由 提到路由&#xff08;Route&#xff09;&#xff0c;一般我们会联想到网络中常见的路由器&#xff08;Router&#xff09;&#xff0c;那么路由和路由器之间有什么关联呢&#xff1f;路由是指路由器从一个接口接收到数据&#xff0c;根据数据的目的地址将数据定向传送…
阅读更多...
git-删除workspace.xml的跟踪

git-删除workspace.xml的跟踪

问题描述 .gitignore 文件内容如下&#xff1a; .pyc *.pyc user_files/ .vscode/ __pycache__//.idea/misc.xml /.idea/modules.xml /.idea/inspectionProfiles/profiles_settings.xml /.idea/inspectionProfiles/Project_Default.xml /.idea/batrp_webbackend-server-dev.i…
阅读更多...
Java 开发 框架安全：Spring 漏洞序列.（CVE-2022-22965）

Java 开发 框架安全：Spring 漏洞序列.（CVE-2022-22965）

什么叫 Spring 框架. Spring 框架是一个用于构建企业级应用程序的开源框架。它提供了一种全面的编程和配置模型&#xff0c;可以简化应用程序的开发过程。Spring 框架的核心特性包括依赖注入&#xff08;Dependency Injection&#xff09;、面向切面编程&#xff08;Aspect-Or…
阅读更多...
【Linux笔记】 基础指令（二）

【Linux笔记】 基础指令（二）

风住尘香花已尽 日晚倦梳头 重命名、剪切指令 -- mv 简介&#xff1a; mv 命令是 move 的缩写&#xff0c;可以用来移动文件或者将文件改名&#xff0c;是 Linux 系统下常用的命令&#xff0c;经常用来备份文件或者目录 语法&#xff1a; mv [选项] 源文件或目录 目标文件或目录…
阅读更多...
笨方法自学python（三）-数学计算

笨方法自学python（三）-数学计算

数字和数学计算 这章练习里有很多的数学运算符号。我们来看一遍它们都叫什么名字 plus 加号-minus 减号/ slash 斜杠*asterisk 星号% percent 百分号< less-than 小于号greater-than 大于号< less-than-equal 小于等于号 greater-than-equal 大于等于号 print ("I …
阅读更多...
刷t2、、、

刷t2、、、

、、 public class ThisTest {public static void main(String args[]) {int i;for (;;) {System.out.println(1);}} } while()的循环条件等于for中循环条件。循环体会有一个条件改变等于for中类似自增条件。while()判断条件一般在while前面会初始化跟for中初始化一样。这样 w…
阅读更多...
【讲解下目标追踪】

【讲解下目标追踪】

&#x1f308;个人主页: 程序员不想敲代码啊 &#x1f3c6;CSDN优质创作者&#xff0c;CSDN实力新星&#xff0c;CSDN博客专家 &#x1f44d;点赞⭐评论⭐收藏 &#x1f91d;希望本文对您有所裨益&#xff0c;如有不足之处&#xff0c;欢迎在评论区提出指正&#xff0c;让我们共…
阅读更多...
ECharts系列文章汇总（持续更新中）

ECharts系列文章汇总（持续更新中）

ECharts介绍 ECharts是一款基于JavaScript的数据可视化图表库&#xff0c;提供了直观、生动、可交互、可个性化定制的数据可视化图表。以下是关于ECharts的详细介绍&#xff1a; 发展历程&#xff1a; ECharts最初由百度团队开源&#xff0c;并在2018年初捐赠给Apache基金会&…
阅读更多...
软件工程经济学--期末复习资料

软件工程经济学--期末复习资料

软件工程经济学--期末复习资料 前言第一章 绪论第二章 软件工程经济学基础第三章 软件的成本管理与定价分析第四章 软件工程项目评价方法与经济效果评价第五章 软件生产函数、效益分析及不确定性分析第六章 软件工程项目进度计划的制定结尾总结 前言 软件工程经济学&#xff0…
阅读更多...
Github2024-05-10开日报 Top10

Github2024-05-10开日报 Top10

根据Github Trendings的统计&#xff0c;今日(2024-05-10统计)共有10个项目上榜。根据开发语言中项目的数量&#xff0c;汇总情况如下&#xff1a; 开发语言项目数量Python项目4TypeScript项目4JavaScript项目1Lua项目1C项目1Rust项目1Dart项目1 RustDesk: 用Rust编写的开源远…
阅读更多...
如何映射公司的BS架构系统，出差也能远程访问？

如何映射公司的BS架构系统，出差也能远程访问？

在现代企业运营中&#xff0c;员工出差和分支机构的协同工作变得越来越普遍。然而&#xff0c;如何确保在不同地点的员工都能安全、便捷地访问公司内网的BS&#xff08;Browser/Server&#xff09;架构办公系统&#xff0c;是一个亟待解决的问题。 贝锐花生壳内网穿透服务提供…
阅读更多...
vue 路由url中去掉＃

vue 路由url中去掉＃

修改前效果 想要去掉/# 如何实现&#xff1f; 1、typeScript中去掉url中# 找到项目中的router/index.ts-----------去掉createWebHashHistory中的Hash 将createWebHashHistory修改为createWebHistory 2、javaScript中去掉url中# 找到项目中的router/index.js-----------添加…
阅读更多...
如何批量将十六进制数据转成bin文件

如何批量将十六进制数据转成bin文件

最近在做新项目遇到一个问题&#xff0c;我们要通过上位机把一堆数据通过串口发送给下位机存储&#xff0c;而上位机需要Bin文件。 解决办法&#xff1a; 1)创建一个记事本文件&#xff0c;然后将其后缀修改成.bin 2)然后打开notepad,新建一个文件&#xff0c;随便写下数据 我…
阅读更多...
2024年第九届数维杯大学生数学建模挑战赛B 题思路1.0版本

2024年第九届数维杯大学生数学建模挑战赛B 题思路1.0版本

B题&#xff1a;生物质和煤共热解问题的研究 数维杯分享资料&#xff08;问题一代码论文思路&#xff09;链接&#xff08;18点更新&#xff09;&#xff1a; 链接&#xff1a;https://pan.baidu.com/s/1GSv9dkqcY6G-XUnd0sJe_A 提取码&#xff1a;sxjm 题目分析&#xff1…
阅读更多...
RFID在汽车制造中的应用如何改变行业

RFID在汽车制造中的应用如何改变行业

随着工业4.0和中国制造2025的推进&#xff0c;企业对于智能化、自动化的需求日益增长&#xff0c;RFID射频技术在制造业中已经相当普遍了。在如今这瞬息万变的行业与时代中&#xff0c;RFID技术可以帮助企业获得竞争优势&#xff0c;简化日益复杂的生产流程&#xff0c;推动企业…
阅读更多...
Ansible的安装与基础命令的使用

Ansible的安装与基础命令的使用

Ansible Ansible 是一个开源的自动化工具&#xff0c;用于配置管理、应用部署和任务自动化。它由 Michael DeHaan 于 2012 年创建&#xff0c;后来被 Red Hat 收购。Ansible 的设计理念是简单易用&#xff0c;不需要在受管节点上安装任何代理软件&#xff0c;它通过 SSH&#…
阅读更多...
使用 scrapyd 部署 scrapy

使用 scrapyd 部署 scrapy

1.scrapyd 是什么&#xff1f; Scrapyd 是一个用于部署和运行 Scrapy 爬虫项目的服务器应用程序。它使得你可以通过 HTTP 命令来部署、管理和执行多个 Scrapy 爬虫&#xff0c;非常适合持续集成和生产环境中的爬虫部署。 2.安装scrapyd 并使用 2.1 安装 scrapyd F:\scrapydTes…
阅读更多...
飞跨电容型的三电平（FC-NPC）逆变器simulink仿真模型

飞跨电容型的三电平（FC-NPC）逆变器simulink仿真模型

本人搭建了飞跨电容型的三电平逆变器simulink仿真模型&#xff0c;相较于二极管钳位型三电平逆变器而言&#xff0c;钳位二极管变为飞跨的电容。采用SPWM调制和均流均压控制&#xff0c;通过搭建仿真模型得到三电平波形。 三电平拓扑中的飞跨电容是指在电路的输出端使用电容来实…
阅读更多...
[YOLOv8] 用YOLOv8实现指针式圆形仪表智能读数(三)

[YOLOv8] 用YOLOv8实现指针式圆形仪表智能读数(三)

最近研究了一个项目&#xff0c;利用python代码实现指针式圆形仪表的自动读数&#xff0c;并将读数结果进行输出&#xff0c;若需要完整数据集和源代码可以私信。 目录 &#x1f353;&#x1f353;1.yolov8实现圆盘形仪表智能读数 &#x1f64b;&#x1f64b;2.表盘智能读数…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023