🎁个人主页:我们的五年
🔍系列专栏:C语言基本概念
🌷追光的人,终会万丈光芒
🎉欢迎大家点赞👍评论📝收藏⭐文章


目录
🚗1.对栈概念理解:
🚗2.选择哪种数据结构实现栈:
🎉数组:
🎉链表:
🚗3.栈的几个基本操作函数:
🎉1.栈的初始化:
🎉2.栈的销毁:
🎉3.栈的初始化:
🎉4.取栈顶元素:
🎉5.对栈判空,为空返回true,不为空返回false:
🎉6.销毁栈顶元素:
🎉7.获取栈里面的元素个数:
前言:
本次让我们来学习栈,以及对前面学习的顺序表和链表进行一个比较。
喜欢的铁子可以支持一下!祝大家天天开心!
🚗1.对栈概念理解:
栈的特点:先进后出。
入栈:栈的插入操作叫做进栈/压栈/入栈,入数据在栈顶。
出栈:栈的删除操作叫做出栈,出数据也在栈顶。
栈是和顺序表很像,我觉得是一种特殊的顺序表。栈只允许从一端进行插入和删除(访问一次就等于一次删除,就是出栈),但是可以同时进行插入和删除操作,不一定要把全部的数据入栈以后,再进行出栈。
●现实生活中栈的模型:弹夹,先装进去的子弹后出来,后装进去的子弹先被打出来。
●但是,下面的图形象化,更好理解。
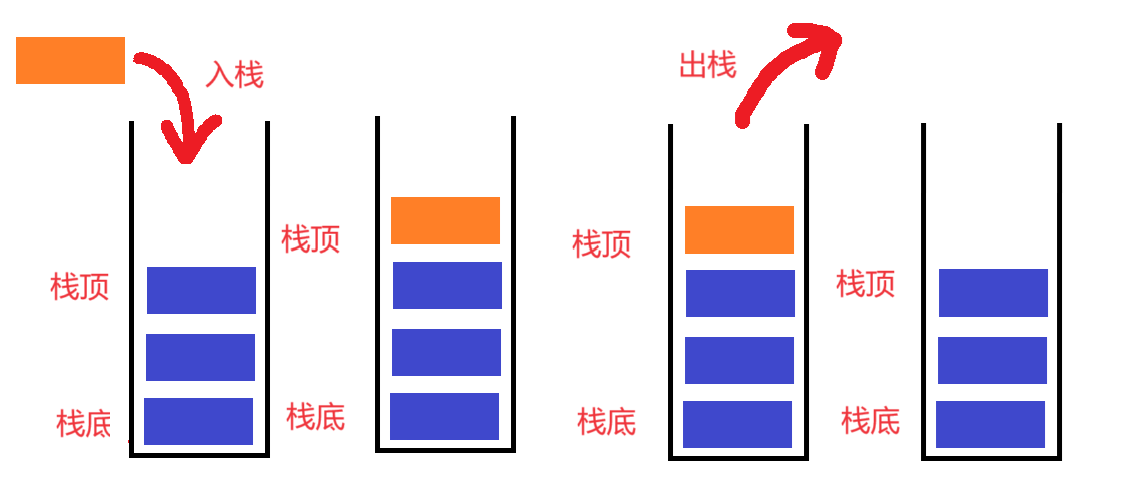
上面的表示的就是栈只能从一边入,也只能从这一边出数据。但是我可以入一个就出一个。也可以入两个,然后出一个,然后在入栈。
🚗2.选择哪种数据结构实现栈:
我们知道,栈就是一种线性结构,但是前面我们学的线性结构有数组,链表。
🎉数组:
●物理(内存)上连续,逻辑上也连续:
数组的顺序存储结构,采用一组连续的内存来存储数据。
数组的线性关系是在内存(物理)上的相邻关系来表示数组的逻辑关系,也就是说,数组的连续和线性依靠的是内存的连续和线性。
●数组内存是连续的,所以可以随机访问,读取效率很高。
●数组在进行插入时,在下表为i的位置之前插入数据,需要把[i,n-1]的数据往后面移动,才能进行插入数据。但是如果在尾部插入就不需要对数组进行移动。
●数组在开辟的时候就要确定大小,如果是动态内存,后面进行增容的时候,还要考虑后面的空间知否足够,如果不足够,还要找一块新的内存,把之前的数据进行拷贝。因为是确定了大小了的,所以有时候会浪费空间。
🎉链表:
●物理(内存)上不连续,逻辑上连续:
链表是链式存储结构,链表的内存(物理)不一定是连续的,但是逻辑上是连续的。也就是可以通过节点一找到节点二,节点二可以找到节点……
●因为上面这种链式结构,所以链表的读取效率低,要读取数据,要去遍历链表。
●链表只是逻辑连续,所以在进行插入删除时也更方便。不需要对数据进行移动,只需要把新的节点与原来的链表建立联系。
●链表定义的时候,没有确定大小,所以链表的增容也更方便。
根据以上数组和链表的区别,我们可以思考在实现栈的时候,那种数据结构更好,因为栈只能在一端插入删除数据,插入删除数据的时候,只是在尾部进行插入删除,就不要去移动数据位置,这样我们就选择数组实现栈。
🚗3.栈的几个基本操作函数:
和顺序表和链表一样,都是自定义的结构体类型,所以我们要去实现一下它的几个基本函数。比如:栈的初始化,栈的销毁,入栈,出栈……
🎉1.栈的初始化:
//栈的初始化
void StackInit(Stack* ptr)
{
assert(ptr);
ptr->a = NULL;
ptr->capacity = ptr->top = 0;
}❗️注意:
1.一开始我们把top置为0,也就是说,没有数据的时候,top=0,top和元素个数的大小是一样的。
2.top=0,下次我们要插入数据的时候,也是在下标为0的位置进行插入,所以这是top表示的是栈顶元素的下一位。
3.如果我们一开始把top=-1,就表示当前栈顶元素的下标。插入一个元素以后,top=0,插入的数据下标也是0,所以这个时候的top表示栈顶元素的下标。
🎉2.栈的销毁:
//销毁栈
void StackDestroy(Stack* ptr)
{
assert(ptr);
free(ptr->a);
ptr->a = NULL;
ptr->capacity = ptr->top = 0; //初始化时,top=0,表示指向栈顶的下一个元素
}
🎉3.栈的初始化:
//在栈顶插入元素
void StackPush(Stack* ptr, SLDataType x)
{
assert(ptr);
if (ptr->top == ptr->capacity)
{
int newcapacity = ptr->capacity == 0 ? 4 : ptr->capacity * 2;
SLDataType* tmp = (SLDataType*)realloc(ptr->a, newcapacity*sizeof(SLDataType));
if (tmp == NULL)
{
perror("realloc fail");
return;
}
ptr->a = tmp;
ptr->capacity = newcapacity;
}
ptr->a[ptr->top++] = x;
}❗️注意:
1.因为我们在栈的初始化的时候,我们没有申请数组大小,所以我们在插入数据在进行判断是否数据已经存满的时候,我们要去考虑数据个数为0的情况。
🎉4.取栈顶元素:
//取栈顶元素
SLDataType StackTop(Stack* ptr)
{
assert(ptr);
assert(!StackEmpty(ptr));
return ptr->a[ptr->top - 1];
}
🎉5.对栈判空,为空返回true,不为空返回false:
//栈判空
bool StackEmpty(Stack* ptr)
{
assert(ptr);
return ptr->top == 0;
}
🎉6.销毁栈顶元素:
//销毁栈顶元素
void StackPop(Stack* ptr)
{
assert(ptr);
assert(!StackEmpty(ptr));ptr->top--;
}
🎉7.获取栈里面的元素个数:
//获取栈里面元素个数
int StackSize(Stack* ptr)
{
assert(ptr);return ptr->top;
}
说明:
上面有些函数只有一条语句,我们还写成函数的形式,看上去感觉没有必要。但是当我们把我们写的函数给别人用,别人只要调用这些函数就可以了,就不会出错。
比如:没有函数,让别人使用的时候,当别人要去栈顶的元素,别人就不知道到底是top指向栈顶元素的下标,还是top-1是栈顶元素的下标。因为top初始化为0时,top-1指向指向栈顶元素的下标,top初始化为-1时,top指向栈顶元素的下标。
🚗4.栈的总体代码:
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>
typedef int SLDataType;
typedef struct Stack{
SLDataType* a;
int top;
int capacity;
}Stack;
//对栈进行初始化
void StackInit(Stack* ptr);
//对栈进行销毁
void StackDestroy(Stack* ptr);
//在栈顶插入元素
void StackPush(Stack* ptr, SLDataType x);
//获取栈顶元素
SLDataType StackTop(Stack* ptr);
//对栈进行判断,如果为空,返回true,否则返回false
bool StackEmpty(Stack* ptr);
//获取栈里面的元素个数
int StackSize(Stack* ptr);
void StackPop(Stack* ptr);
//栈的初始化
void StackInit(Stack* ptr)
{
assert(ptr);
ptr->a = NULL;
ptr->capacity = ptr->top = 0;
}
//销毁栈
void StackDestroy(Stack* ptr)
{
assert(ptr);
free(ptr->a);
ptr->a = NULL;
ptr->capacity = ptr->top = 0; //初始化时,top=0,表示指向栈顶的下一个元素
}
//在栈顶插入元素
void StackPush(Stack* ptr, SLDataType x)
{
assert(ptr);
if (ptr->top == ptr->capacity)
{
int newcapacity = ptr->capacity == 0 ? 4 : ptr->capacity * 2;
SLDataType* tmp = (SLDataType*)realloc(ptr->a, newcapacity*sizeof(SLDataType));
if (tmp == NULL)
{
perror("realloc fail");
return;
}
ptr->a = tmp;
ptr->capacity = newcapacity;
}
ptr->a[ptr->top++] = x;
}
//取栈顶元素
SLDataType StackTop(Stack* ptr)
{
assert(ptr);
assert(!StackEmpty(ptr));
return ptr->a[ptr->top - 1];
}
//栈判空
bool StackEmpty(Stack* ptr)
{
assert(ptr);
return ptr->top == 0;
}
//销毁栈顶元素
void StackPop(Stack* ptr)
{
assert(ptr);
assert(!StackEmpty(ptr));
ptr->top--;
}
//获取栈里面元素个数
int StackSize(Stack* ptr)
{
assert(ptr);
return ptr->top;
}