一、算法介绍

快速排序(Quick sort)是由C.A.R.Hoare提出来的。快速排序法又叫分割交换排序法，是目前公认的最佳排序法，也是使用“分而治之”的方式，会先在数据中找到一个虚拟的中间值，并按此中间值将所有打算排序的数据分为两部分。其中小于中间值的数据在左边，而大于中间值的数据在右边，再以同样的方式分别处理左、右两边的数据，直到排序完为止。下面是快速排序的一些基本原理和步骤：

1. 选择基准（Pivot Selection）：

• 从待排序的数组中选择一个元素作为基准值（pivot）。
• 常见的选择方式有：选择第一个元素、最后一个元素或随机选择一个元素。

2. 分区（Partitioning）：

• 将数组中的其他元素与基准值进行比较，将小于基准值的元素移动到基准值的左边，大于基准值的元素移动到基准值的右边。
• 这一步完成后，基准值被放在了最终排序后的正确位置上，数组被分为两部分，左边的元素都小于基准，右边的元素都大于基准。

3. 递归排序（Recursion）：

• 对基准值左边的子数组和右边的子数组分别重复上述步骤，即选择新的基准并进行分区操作。
• 这是一个递归过程，直到子数组只有一个或零个元素，排序结束。

快速排序的平均时间复杂度是O($n\log n$)，在最坏的情况下（例如输入数组已经排序或几乎排序），时间复杂度会退化到O($n^2$)。为了避免这种情况，通常会采用随机化选择基准的方法来提高性能的稳定性。

二、使用迭代的方式实现快速排序

以下是java代码示例：

package com.datastructures;

import java.util.*;

/**
 * 迭代方式实现快速排序算法
 * @author hulei
 */
public class QuickSortIterative {

    //随机枢轴索引生成器
    private static final Random RANDOM = new Random();

    /**
     * 使用快速排序算法对给定的数组进行排序。
     *
     * @param array 待排序的数组，数组元素必须实现Comparable接口。
     * @param <E> 数组元素的类型，该类型需扩展自Comparable，以支持元素之间的比较。
     */
    public static <E extends Comparable<? super E>> void quickSortIterative(E[] array) {
        // 如果数组为空或长度小于等于1，则无需排序，直接返回
        if (array == null || array.length <= 1) {
            return;
        }

        // 使用栈来实现分治法中的递归调用（迭代方式）
        Stack<Integer> stack = new Stack<>();
        // 初始化栈，分别入栈数组的起始和结束索引
        stack.push(0);
        stack.push(array.length - 1);
        int cycle = 0;
        // 当栈不为空时,持续进行排序
        while (!stack.isEmpty()) {
            int high = stack.pop(); // 取出栈顶，为当前区间上界
            int low = stack.pop();  // 再次取出栈顶，为当前区间下界
            cycle++;
            System.out.println("第"+cycle+"轮循环交换开始");
            // 对当前区间进行划分,返回枢轴元素的最终位置
            int pivotIndex = partition(array, low, high);
            System.out.println("第"+cycle+"轮循环交换结束,枢轴已放置到正确位置上");
            System.out.println("第一轮交换后的结果："+Arrays.toString(array)+",枢轴元素为："+array[pivotIndex]);
            System.out.println("=========================================================================");
            // 如果枢轴元素左边还有未排序的元素,则将其入栈
            //pivotIndex - 1 > low说明当前分区左边起始索引到枢轴位置索引之间还有至少一个元素,根据当前排序结果只能保证枢轴左边所有的元素都是小于枢轴元素,
            // 但是不能保证左边起始索引到枢轴位置索引之间的元素都大于起始索引位置元素，或者内部已经排序过，所以需要再次进行排序
            if (pivotIndex - 1 > low) {
                stack.push(low);
                stack.push(pivotIndex - 1);
            }
            // 如果枢轴元素右边还有未排序的元素,则将其入栈
            //pivotIndex + 1 < high说明当前分区右边起始索引到枢轴位置索引之间还有至少一个元素,根据当前排序结果只能保证枢轴右边所有的元素都是大于枢轴元素,
            // 但是不能保证右边枢轴位置索引到右边结束位置索引之间的元素都小于结束索引位置元素，或者内部已经排序过，所以需要再次进行排序
            if (pivotIndex + 1 < high) {
                stack.push(pivotIndex + 1);
                stack.push(high);
            }
            //综上分区结束时，枢轴左右两边都各只能有且最多一个元素，所以不需要再次进行排序
        }
    }

    /**
     * 对给定区间进行划分，返回枢轴元素的最终位置。
     *
     * @param array 待划分的数组
     * @param low 划分的起始索引
     * @param high 划分的结束索引
     * @return 枢轴元素的最终位置
     */
    private static <E extends Comparable<? super E>> int partition(E[] array, int low, int high) {
        // 随机选择一个元素作为枢轴(枢轴的索引范围为[low, high])
        //这个表达式 RANDOM.nextInt((right - left) + 1) + left
        //RANDOM.nextInt((right - left) + 1)方法生成的是 [0, (right - left+1))范围内的非负随机整数即为,包含左端点0，不包含右端点right - left+1
        //实际上，这个表达式生成的随机整数的范围是 [0, right - left],包括left和right两个端点。
        //加上 left 后，范围变成了 [left, right]，确保了包含两个端点。
        int pivotIndex = RANDOM.nextInt((high - low) + 1) + low;
        //取基准值
        E pivot = array[pivotIndex];
        System.out.println("随机枢轴元素pivot:"+pivot);
        // 将随机选中的枢轴元素与数组末尾元素交换,便于后续处理
        swap(array, pivotIndex, high);
        System.out.println("把随机枢轴元素放到数组末尾后的结果："+Arrays.toString(array));
        System.out.println();
        int i = low - 1;
        for (int j = low; j < high; j++) {
            System.out.println("交换前数组："+Arrays.toString(array));
            System.out.print("i指针索引初始值为："+i+"----");
            if (array[j].compareTo(pivot) <= 0) {
                i++;
                System.out.println("j指针索引当前值为:"+j+" 对应元素为："+array[j]+" 小于枢轴元素值："+pivot+" i指针向右边移动一位变为:"+i);
                System.out.println("array[i]="+"array["+i+"]="+array[i]+",array[j]=array["+j+"]="+array[j]+",交换array[i]和array[j]元素位置");
                swap(array, i, j);
                System.out.println("array[i]="+"array["+i+"]="+array[i]+",array[j]=array["+j+"]="+array[j]+",交换后数组："+Arrays.toString(array));
            }else{
                System.out.println("j指针索引初始值为:"+j+" 指针对应元素为："+array[j]+" 大于枢轴元素："+pivot);
                System.out.println("数组元素不交换："+Arrays.toString(array));
            }
            System.out.println();
        }
        swap(array, i + 1, high); // 将枢轴元素放回正确的位置
        return i + 1;
    }

    /**
     * 交换数组中两个元素的位置。
     * @param array 要进行交换的数组。
     * @param index1 要交换的第一个元素的索引。
     * @param index2 要交换的第二个元素的索引。
     * @param <E> 数组元素的类型。
     */
    private static <E> void swap(E[] array, int index1, int index2) {
        // 临时变量用于存储第一个元素，以便后续交换
        E temp = array[index1];
        array[index1] = array[index2]; // 将第二个元素的值赋给第一个元素
        array[index2] = temp; // 将之前存储的第一个元素的值赋给第二个元素
    }

    public static void main(String[] args) {
        Integer[] arr = new Integer[]{20, 12, 27, 15, 18, 21, 34, 28, 23, 41, 39, 14, 6, 17};
        System.out.println("原始数组:");
        System.out.println(Arrays.toString(arr));
        System.out.println();
        quickSortIterative(arr);
        System.out.println("快速排序后数组:");
        System.out.println(Arrays.toString(arr));
    }
}

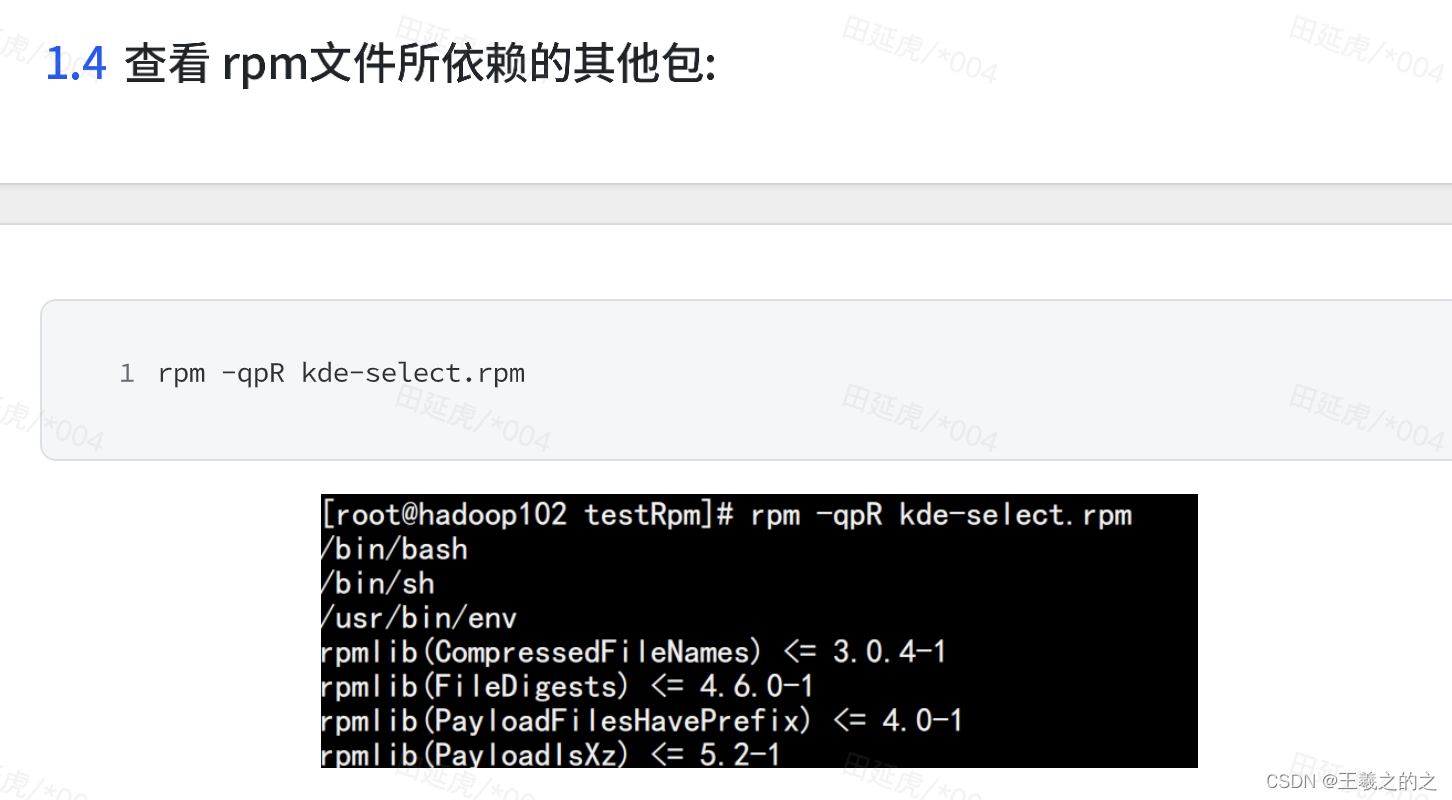
笔者认为快速排序不是那么容易理解，所以在代码中加入了很多打印信息，以此来更加直观明了的展示快速排序的交换过程，因为打印的排序过程信息比较长，这里只截取开始部分的截图，建议自行把代码复制到IDE中运行下，查看控制台信息，加深理解。注释写的已经很清楚了，看不懂的话需要细细揣摩，或者自行把待排序的数组调整的简单点运行观察。
如第一轮是整个数组选取基准值pivot后排序。排序结束后所有小于pivot的值放在它的左边，大于pivot的值放在它的右边
第二轮和第三轮分别是对第一轮分区后的左分区和右分区，分别选取各自分区的基准值pivot后再排序，大于pivot的放右边，小于pivot的放左边
。
。
。
以此类推，持续进行分区排序**，每次分区排序处理后，判断枢轴元素分别到左起始索引和右结束索引之间是否还有元素**，如果有，则需要把当前分区的左起始索引到枢轴索引前一个位置的索引当作新的左分区入栈处理，枢轴索引后一个索引位置到当前分区的结束索引范围当作新的右分区入栈处理。

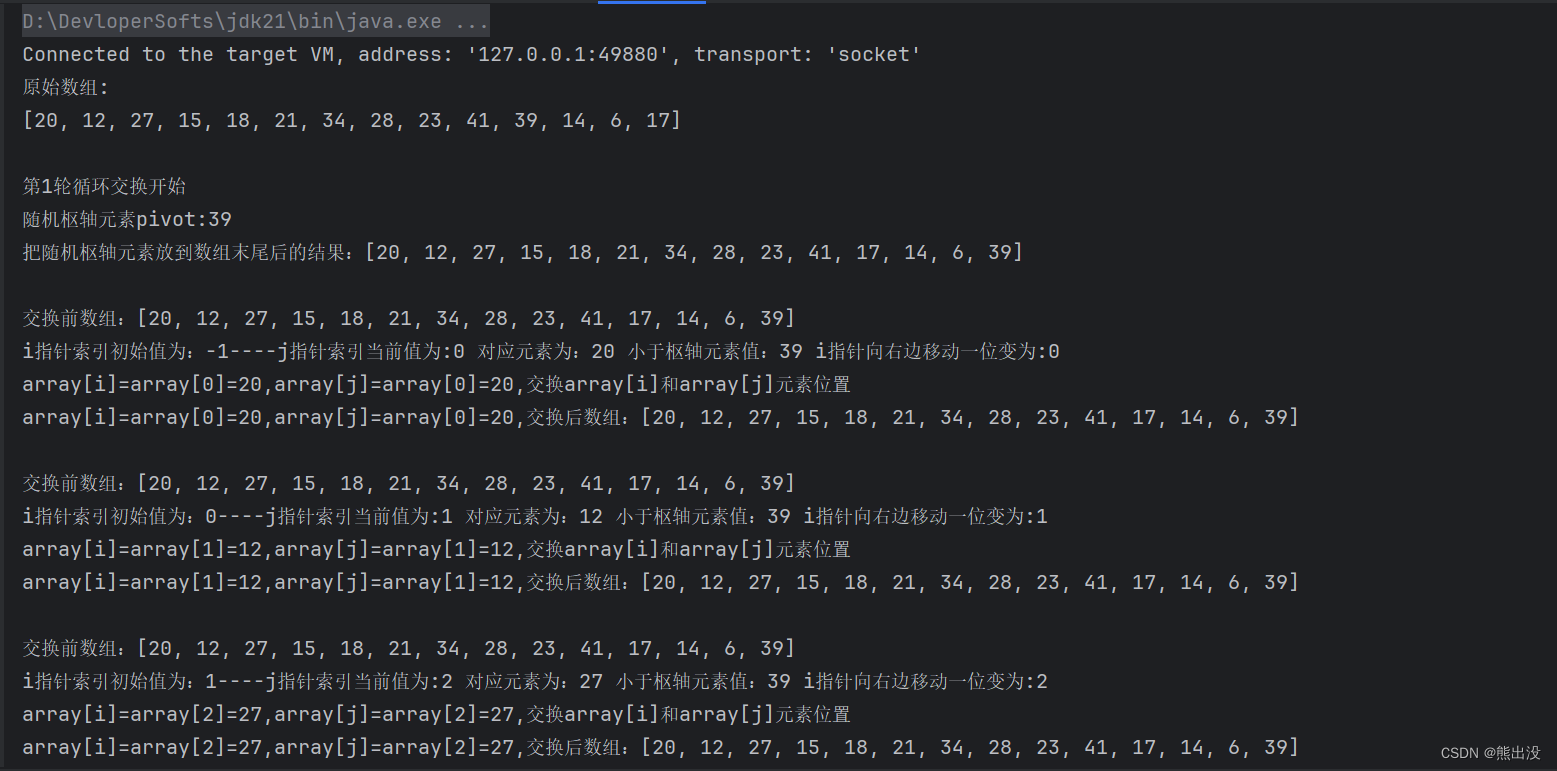
分区方法partition()里在随机选择好枢轴元素后，交换放置到数组的最后一位high的位置是为了方便遍历比较，只需要考虑枢轴左边的所有元素，不用考虑枢轴本身。如果不把枢轴元素放到最后一位，那么在遍历时，索引在枢轴元素左边的容易处理，一旦索引遍历到超过枢轴元素时，如果发现元素值小于枢轴元素，则需要把枢轴元素往前移，即交换位置，这样处理非常麻烦且性能差，基本不考虑了(其实是我试了很多次都没有成功。。。。哈哈哈)

代码里使用了Stack，这是JDK提供的实现了栈的数据结构特点的一个官方实现类，使用Stack主要有下面几个原因：

1. 避免递归带来的栈溢出风险： 快速排序的经典实现通常采用递归方法，递归在处理大规模数据时可能会导致调用栈过深，引发StackOverflowError。通过使用Stack作为迭代结构，可以将递归转换为循环，从而有效避免了栈溢出的问题。

2. 控制排序过程的迭代逻辑：
Stack用于存储待排序区间的边界索引（即low和high）。每次循环从栈顶弹出两个元素作为当前区间的上下界，对这个区间进行排序。如果排序后发现枢轴元素的左侧或右侧还有未排序的子区间，则将这些子区间的边界索引重新压入栈中，等待后续循环处理。这样，直到栈为空，所有子区间都被排序，整个数组也就完成了排序。

3. 提高空间效率：
相比于递归调用时系统自动管理的调用栈，手动管理的Stack可以在一定程度上减少内存使用。尽管这种差异在小规模数据上可能不明显，但在处理大量数据时，自定义栈可以更精细地控制所需的空间。

4. 增强代码可读性和灵活性：
通过显式地使用Stack来模拟递归逻辑，代码的意图更加清晰，便于理解和维护。同时，这也为后续可能的优化提供了便利，比如可以通过调整压栈顺序来改变排序策略，或者在栈操作中加入额外的逻辑来适应特定需求。

三、使用递归的方式实现快速排序

递归方式的java代码如下：

package com.datastructures;

import java.util.Arrays;
import java.util.Random;

/**
 * 递归方式实现快速排序算法
 * @author hulei
 * @date 2024/5/6 15:19
 */


public class QuickSortRecursive {
    //随机枢轴索引生成器
    private static final Random RANDOM = new Random();

    private static int cycle = 0;

    public static void main(String[] args) {
        Integer[] arr = new Integer[]{20, 12, 27, 15, 18, 29, 11, 21, 34, 28, 23, 41, 39, 14, 6, 17};
        System.out.println("原始数组:");
        System.out.println(Arrays.toString(arr));
        System.out.println();
        quickSortWithRecursive(arr, 0, arr.length - 1);
        System.out.println("快速排序后数组:");
        System.out.println(Arrays.toString(arr));
    }

    /**
     * 递归方式快速排序
     *
     * @param array 待排序数组
     * @param left  排序起始索引
     * @param right 排序结束索引
     */
    private static <E extends Comparable<? super E>> void quickSortWithRecursive(E[] array, int left, int right) {
        if (left >= right) {
            return;
        }
        cycle++;
        System.out.println("第" + cycle + "轮循环交换开始");
        // 对当前区间进行划分,返回枢轴元素的最终位置
        int pivotIndex = partition(array, left, right);
        System.out.println("第" + cycle + "轮循环交换结束,枢轴已放置到正确位置上");
        System.out.println("第一轮交换后的结果：" + Arrays.toString(array) + ",枢轴元素为：" + array[pivotIndex]);
        // 如果枢轴元素左边还有未排序的元素,则继续递归排序
        //pivotIndex - 1 > left说明当前分区左边起始索引到枢轴位置索引之间还有至少一个元素,根据当前排序结果只能保证枢轴左边所有的元素都是小于枢轴元素,
        // 但是不能保证左边起始索引到枢轴位置索引之间的元素都大于起始索引位置元素，或者内部已经排序过，所以需要再次进行排序
        if (pivotIndex - 1 > left) {
            quickSortWithRecursive(array, left, pivotIndex - 1);
        }
        // 如果枢轴元素右边还有未排序的元素,则继续递归排序
        //pivotIndex + 1 < high说明当前分区右边起始索引到枢轴位置索引之间还有至少一个元素,根据当前排序结果只能保证枢轴右边所有的元素都是大于枢轴元素,
        // 但是不能保证右边枢轴位置索引到右边结束位置索引之间的元素都小于结束索引位置元素，或者内部已经排序过，所以需要再次进行排序
        if (pivotIndex + 1 < right) {
            quickSortWithRecursive(array, pivotIndex + 1, right);
        }
    }

    /**
     * 划分函数
     *
     * @param array 待排序数组
     * @param left  排序起始索引
     * @param right 排序结束索引
     * @return 返回枢轴元素的最终位置
     */
    private static <E extends Comparable<? super E>> int partition(E[] array, int left, int right) {
        // 随机选择一个元素作为枢轴(枢轴的索引范围为[low, high])
        //这个表达式 RANDOM.nextInt((right - left) + 1) + left
        //RANDOM.nextInt((right - left) + 1)方法生成的是 [0, (right - left+1))范围内的非负随机整数即为,包含左端点0，不包含右端点right - left+1
        //实际上，这个表达式生成的随机整数的范围是 [0, right - left],包括left和right两个端点。
        //加上 left 后，范围变成了 [left, right]，确保了包含两个端点。
        int pivotIndex = RANDOM.nextInt((right - left) + 1) + left;
        //取基准值
        E pivot = array[pivotIndex];
        System.out.println("随机枢轴元素pivot:" + pivot);
        // 将随机选中的枢轴元素与数组末尾元素交换,便于后续处理
        swap(array, pivotIndex, right);
        System.out.println("把随机枢轴元素放到数组末尾后的结果：" + Arrays.toString(array));
        System.out.println();
        int i = left - 1;
        for (int j = left; j < right; j++) {
            System.out.println("交换前数组：" + Arrays.toString(array));
            System.out.print("i指针索引初始值为：" + i + "----");
            if (array[j].compareTo(pivot) <= 0) {
                i++;
                System.out.println("j指针索引当前值为:" + j + " 对应元素为：" + array[j] + " 小于枢轴元素值：" + pivot + " i指针向右边移动一位变为:" + i);
                System.out.println("array[i]=" + "array[" + i + "]=" + array[i] + ",array[j]=array[" + j + "]=" + array[j] + ",交换array[i]和array[j]元素位置");
                swap(array, i, j);
                System.out.println("array[i]=" + "array[" + i + "]=" + array[i] + ",array[j]=array[" + j + "]=" + array[j] + ",交换后数组：" + Arrays.toString(array));
            } else {
                System.out.println("j指针索引初始值为:" + j + " 指针对应元素为：" + array[j] + " 大于枢轴元素：" + pivot);
                System.out.println("数组元素不交换：" + Arrays.toString(array));
            }
            System.out.println();
        }
        swap(array, i + 1, right); // 将枢轴元素放回正确的位置
        return i + 1;
    }

    /**
     * 交换数组中两个元素的位置。
     *
     * @param array  要进行交换的数组。
     * @param index1 要交换的第一个元素的索引。
     * @param index2 要交换的第二个元素的索引。
     * @param <E>    数组元素的类型。
     */
    private static <E> void swap(E[] array, int index1, int index2) {
        // 临时变量用于存储第一个元素，以便后续交换
        E temp = array[index1];
        array[index1] = array[index2]; // 将第二个元素的值赋给第一个元素
        array[index2] = temp; // 将之前存储的第一个元素的值赋给第二个元素
    }

}

代码逻辑和迭代方式差不多，这里不再解释

四、迭代和递归方式处理快速排序的选择比较

递归方式的逻辑和迭代方式逻辑基本差不多，二者的分区处理逻辑是一样的，即**partition（）**函数逻辑一致。唯一的区别是分区后持续处理分区的排序方式不同，迭代器方式通过Stack临时存储分区信息，再使用while循环处理栈数据，而递归方式代码逻辑相对简单点，分区后判断是否需要处理分区排序，递归调用函数自身实现后续分区和子分区的排序处理。

迭代和递归两者在处理逻辑上基本一致，都是基于分治法的思想，但实现机制有所不同，具体区别如下：

递归方式

• 实现原理：递归方式的快速排序直接体现了算法的定义。它通过选择一个“基准”元素，然后将数组分为两部分，一部分都比基准小，另一部分都比基准大，之后对这两部分分别递归地进行快速排序。
• 代码特点：递归实现相对简洁，逻辑清晰，易于理解。它通过函数自我调用来处理数组的子区间。
• 栈空间：每次函数调用都会在调用栈上分配空间，如果排序的数据量非常大，可能会导致栈溢出。
• 性能考量：递归调用会增加额外的时间开销，包括函数调用的压栈和弹栈操作。此外，大量的递归调用可能导致较高的内存使用。

迭代方式

• 实现原理：迭代方式通常需要借助栈（或队列）等数据结构来模拟递归过程中的函数调用栈。通过手动管理这个栈，控制排序区间，达到与递归相同的效果。
• 代码特点：迭代实现相比递归可能稍微复杂一些，因为它需要显式地管理排序区间的开始和结束索引，以及用于迭代的栈。
• 栈空间：迭代方法可以减少系统调用栈的使用，避免了深度递归可能导致的栈溢出问题，对于大规模数据排序更为安全。
• 性能考量：迭代通常能减少函数调用的开销，提高运行效率，尤其是在没有尾递归优化的编程环境中。它对于内存的使用也更加高效，因为不需要为每次函数调用分配新的栈帧。

总结

选择迭代还是递归实现快速排序，取决于具体的应用场景和需求。递归实现更直观易懂，适合自我学习和小型数据集；而迭代实现则在处理大规模数据时更为稳健，能有效避免栈溢出的风险，并可能在性能上有一定优势。在实际应用中，我们需根据实际情况权衡选择，没有最好的只有最合适的。

五、时间复杂度计算

递归方式

分析

1. partition函数时间复杂度
partition函数遍历了从left到right的所有元素一次，执行了比较和可能的交换操作。因此，这部分的时间复杂度 是线性的，即O(right - left)，也可以简化为O(n)，其中n = right - left + 1是子数组的长度。

2. quickSortWithRecursive函数时间复杂度
快速排序的基本思想是分而治之。在每一轮递归中，算法首先调用partition函数将数组分为两部分，然后对这两部分分别递归地进行排序。
在最好的情况下（每次划分都很均匀），每次递归调用都将问题规模减半，因此递归树的深度为O($\log n$)，每一层的总工作量是线性的（因为每一层都要遍历相应子数组的元素），所以总的时间复杂度是O($n\log n$)。
在最坏的情况下（每次划分都非常不均匀，例如已经排序好的数组或完全逆序的数组），递归树退化为链状结构，每次只减少一个元素，导致递归深度达到n，此时的时间复杂度退化为O($n^2$)。

综合分析

• 平均时间复杂度：O($n\log n$)。这是因为大多数情况下，快速排序能够得到较好的划分，使得递归树的深度接近log n。
• 最好情况时间复杂度：O($n\log n$)，当每次划分都均匀时。
• 最坏情况时间复杂度：O($n^2$)，当数组已经是有序或逆序时。

实际操作中的优化
为了提高实际应用中的性能，快速排序通常会采用一些策略来避免最坏情况的发生，比如笔者在递归的代码中就采用了随机选取枢轴的方法，这有助于平衡划分，使得算法在实际应用中更倾向于O($n\log n$)的平均性能。

迭代方式

主要函数分析

1. quickSortIterative函数
这个函数使用了一个栈来模拟递归调用。对于长度为n的数组，每次对一个子数组进行划分，如果子数组长度为m，则需要进行一次划分操作，时间复杂度为O(m)。
分区操作（partition函数）之后，将小于枢轴的子数组和大于枢轴的子数组分别入栈，继续进行排序。在最坏的情况下，每次划分都只能减少一个元素，导致需要进行n-1次划分，所以时间复杂度为O(n)。
但是，由于每次划分后，我们总是对较小的子数组优先进行操作，因此在平均情况下，每次划分会将问题规模减半，递归树的深度为O(log n)。由于每次划分的时间复杂度是线性的，因此总的时间复杂度是O($n\log n$)。

2. partition函数
partition函数的逻辑与之前的递归版本相同，它遍历了从low到high的所有元素，进行比较和交换操作，时间复杂度为O(high - low)，在最坏情况下为O(n)。

总结

• 最好情况时间复杂度：O($n\log n$)，当每次划分都均匀时。
• 平均情况时间复杂度：O($n\log n$)，这是迭代快速排序的主要时间复杂度，因为它总是优先处理较小的子数组。
• 最坏情况时间复杂度：O($n^2$)，当数组已经是有序或逆序时，每次划分只能减少一个元素。

注意，这里的时间复杂度分析忽略了常数因子和对数项的系数，因为大O表示法主要关注算法在输入规模增长时的主要趋势。

六、学习技巧

快速排序算是几个基础排序算法中比较难理解的了，还有归并排序，更难理解得有堆排序，想彻底理解这些算法的特性，并很自然的能使用代码实现出来，需要多练习，把交换过程打印出来，同时脑子里要有个抽象的动态交换过程图像，可先用几个数尝试，多想象几次就能彻底理解了，笔者就是这么干的。