算法练习day7

四数相加II

代码随想录 0454.四数相加II

454. 四数相加 II - 力扣（LeetCode）

（用时：0.5小时）

思路

本道题是需要在四个数组中，各找一个数，这些数加起来能够等于0，那么就是答案元组。各个数组的数字元组中的位置是固定的，0001和1000是不同的答案。

普通的解法一般是四重循环遍历，逻辑简单粗暴就不再赘述。

这道题可以用哈希表配合进行求解。

先算前两个数组元素相加的结果，将他们的结果存入哈希表中，这里是一个二重循环。

对于前两个数而言，1 2和2 1他们的和虽然都是3，但是情况是不一样的，属于3的情况出现了两次。题目要输出答案元组的个数，因此选择使用hashset。
接着再算后两个数组元素相加结果，通过hashset查找前两个数的和中符合条件的，组成一个完整的答案元组。在此过程中用计数器累加即可。

错误

思路理解的差不多，但是在写的时候，一些细节方面还是出了问题：

累加时，累加的数值出现问题。
（疑问）hashset的key和value取什么

个人理解如下：

（疑问）hashset的key和value取什么

hashset是用来记录前两个数字的和出现情况的。那么key应该是两个数字的和，value应该是这个和出现的频率（次数）。
累加时，累加的数值出现问题。

前面说了，hashset记录的是前两个数字的和出现的频率，那么在累加的时候，应该是要加上频率（次数）而非单纯的加一。

代码实现

hashset实现：

public int FourSumCount(int[] nums1, int[] nums2, int[] nums3, int[] nums4)
{
    int ans = 0, temp;
    Dictionary<int, int> dic = new Dictionary<int, int>();

    //记录前两位相加的结果出现的频率
    foreach (int num1 in nums1)
    {
        foreach (int num2 in nums2)
        {
            if(dic.ContainsKey(num1 + num2))
            {
                dic[num1 + num2]++;
            }
            else
            {
                dic.Add(num1 + num2, 1);
            }
        }
    }

    //计算后两位相加的结果，通过这个结果与最终结果的差值查找是否有前两位的和匹配
    foreach(int num3 in nums3)
    {
        foreach(int num4 in nums4)
        {
            temp = 0 - num3 - num4;

            if(dic.ContainsKey(temp))
            {
                ans+= dic[temp];
            }
        }
    }

    return ans;
}

赎金信

代码随想录 0383.赎金信

383. 赎金信 - 力扣（LeetCode）

（用时：0.3小时）

思路

本题和前面一道四数相加II有点像，只是这道题的变成了两个。

magazine 中的每个字符只能在 ransomNote 中使用一次，那么就不是查看元素出现的频率，而是单纯查看是否出现即可。

字母一共26个（题目假设只看小写）并不多，故用数组实现哈希表。

错误

这道题是比较简单的题，但是在一些细节方面还是出了问题：

看错题，以为是要查看字母出现的频率。
要先处理magazine再处理ransomNote。

个人理解如下：

看错题，以为是要查看字母出现的频率。

这个问题就没什么好说的了。。。查看字母的频率用键值对结构（dictionary）、查看字母是否出现用hashset。数组结构两种都可以用，用数组要看这个表会有多大。
要先处理magazine再处理ransomNote。

题目意思是检验ransomNote的字母在magzine的情况（magazine 中的每个字符只能在 ransomNote 中使用一次）。那么magzine要么是包含ransomNote的关系（返回true），要么就是不匹配的关系（返回false）。

先得得到magzine的元素，再探究ransomNote所有的元素是否在ransomNote出现，且magzine的字母只用一次。

代码实现

/// <summary>
/// 哈希数组实现
/// </summary>
/// <param name="ransomNote"></param>
/// <param name="magazine"></param>
/// <returns></returns>
public bool CanConstruct(string ransomNote, string magazine)
{
    int[] hash = new int[26];

    for (int i = 0; i < magazine.Length; i++)
    {
        hash[magazine[i] - 'a']++;
    }

    for (int i=0;i<ransomNote.Length;i++)
    {
        hash[ransomNote[i] - 'a']--;
    }

    for (int i=0;i<hash.Length;i++)
    {
        if (hash[i]<0)
        {
            return false;
        }
    }

    return true;
}

三数之和

代码随想录 0015.三数之和

15. 三数之和 - 力扣（LeetCode）

（用时：1小时）

思路

和前面的四数相加II不同，本道题是在一个数组中找答案，答案元组不能重复（例如123 和321其实是一个元组）

本题的重点在于去重。

题目是在哈希表章节出现的，去重、唯一性第一反应是用哈希表做。卡哥并没有讲解哈希的方法，因为去重很麻烦

哈希的思路应该是先求出前两项a+b的和，再通过答案和哈希表查找第三项c是否存在。
哈希的结构中，hashset是只记录是否存在，不记录存在次数的，那么可能出现，1 2 1，而1只出现过一次，同一个元素被多次使用。此时感觉可以用键值对的类型来记录出现次数？
但是如果要记录次数，就得配合其他的变量使用。比如让某个数字使用了一次值就--，这是循环一轮时的操作，在新一轮的值又得恢复原本的值。。。这里就很麻烦。
此外，用记录出现次数的键值对类型来做也要额外去重（这里就是卡哥说的去去重麻烦），额外对答案列表中重复的元组去重。
去重的方式其实就是来个二重循环，定一个元组，然后对其他的元组进行遍历比较。这里元组中数字的顺序还不一样，意味着if的条件不能单纯的num1[i]==num2[i]这种，还得处理。

卡哥讲授的是双指针的方法。

一重循环探索确定第一项数字a。
循环中用left和right分别对数字a后的区域进行收缩判断。
这个方法的数组要是有序的。
这中间加上数字a的去重和剪枝操作。

总结来说：

先对数组排序，这里的思路是认为数组升序。
排序后，最外层的循环遍历数字a的情况。

遍历过程中对数字a进行去重，如果此时a的数值已经出现过了，那就向后遍历（因为是有序的，重复的数字会连续出现）。

还可以对数字a剪枝。题目的和固定为是0，那么如果数字a大于0，那么该数组不可能会有答案元组（因为是升序的，数字a是三个数字中最小的）
在确定数字a后，用left和right分别表示数组后续剩下的区域，对这块区域进行收缩。
收缩过程中，如果找到了合适的值就可保留下来。

若nums[i] + nums[left] + nums[right] == 0，表示这组答案是可以的，记录下来即可，然后两个指针一起收缩。若<0，表示目前的有值有点小，那么让left++即可（数组升序）若>0，表示目前的有值有点大，那么让right--即可（同理）
收缩过程中，要对left和right对应的值进行去重。

相同的数值是连续出现的，让left和right指向的值和相邻值不同，即可达到去重的目的。

需要注意的是，去重是在该答案已经有了的情况下才需要对left和right接下来的值进行去重。这说明left和right的去重是要在答案元组被记录下来后的（卡哥提到的“先记录下来再去重”）

疑问点

看完视频和讲解，对解法还是有一些质疑：

疑问1：为什么找到答案时，双指针同时收缩？
疑问2：right和left的去重逻辑和双指针收缩顺序的问题？
疑问3（错误）：数字a的剪枝

个人理解如下：

为什么找到答案时，双指针同时收缩？

找到答案后，i、left和right的值都是固定的。如果只是收缩left或right，加法式子中其中两个加数不变，那么另一个加数的值也应该是固定的，那么此时这组答案应该有了就重复了。
right和left的去重逻辑和双指针收缩顺序的问题？

这里个人认为放在前后都行。

卡哥是先去重，再收缩。收缩比较的是left和left+1（right和right-1）。我个人是right和left的去重逻辑放在双指针收缩前，收缩比较的是left和left-1（right和right+1）。这里顺序与收缩逻辑对应一下就可以了。
数字a的剪枝

这里在写程序时也出现了错误（但是因为是前一天做的，现在忘了这里是怎么错的。。。放上来当作巩固吧）。结果要求是0，数组是升序，那么如果第一个数都大于了0，此数组中想要三个数相加为0是无解的。

代码实现

双指针法：

/// <summary>
/// 双指针法
/// </summary>
/// <param name="nums"></param>
/// <returns></returns>
public IList<IList<int>> ThreeSumFun1(int[] nums)
{
    IList<IList<int>> ans = new List<IList<int>>();
    int left, right;

    Array.Sort(nums);

    for (int i = 0; i < nums.Length; i++)
    {
        if (nums[i] > 0) return ans;

        if (i > 0 && nums[i] == nums[i - 1]) continue;

        left = i + 1;
        right = nums.Length - 1;

        while (left < right)
        {
            if (nums[i] + nums[left] + nums[right] == 0)
            {
                ans.Add(new List<int> { nums[i], nums[left], nums[right] });
                left++;
                right--;

                while (left < right && nums[left] == nums[left - 1]) left++;
                while (left < right && nums[right] == nums[right + 1]) right--;
            }
            else if (nums[i] + nums[left] + nums[right] < 0)
            {
                left++;
            }
            else
            {
                right--;
            }
        }

    }
    return ans;
}

四数之和

代码随想录 0018.四数之和

18. 四数之和 - 力扣（LeetCode）

（用时：2小时）

思路

这道题的思路是在前一道三数之和的基础上的。

三数之和中，哈希法太过复杂，因此卡哥优先讲解的是双指针法，这道题依旧使用的是双指针法。由于多了一个数，因此循环需要多加一层。

本道题就是先确定前两个数字ab，然后依旧用left和right收缩。

错误

写的时候错了一些：

错误1：b剪枝操作的返回值出了问题

个人理解如下：

b剪枝操作的返回值出了问题

在三数之和时，只有一层循环因此在剪枝时，直接让整个函数返回列表也是可以的。这个想法延续要了四数之和，四数之和的第一层循环是和三数一样，因此没有出问题，但是第二层循环不能这么写。

以力扣报错的 -3, -2, -1, 0, 0, 1, 2, 3 这组数据为例。一共是8组答案，程序只判断出了7组，落了一组。经过调试，发现是在-2 0 0 2 这组答案出现后，后面一组的答案没有出现，下图是出现问题前记录的一组答案：

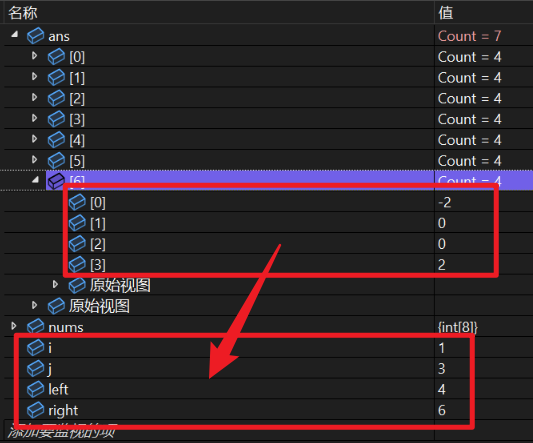
接着往后继续调试，在某一步中，发现第二层循环对b的剪枝操作让函数直接跳出了。

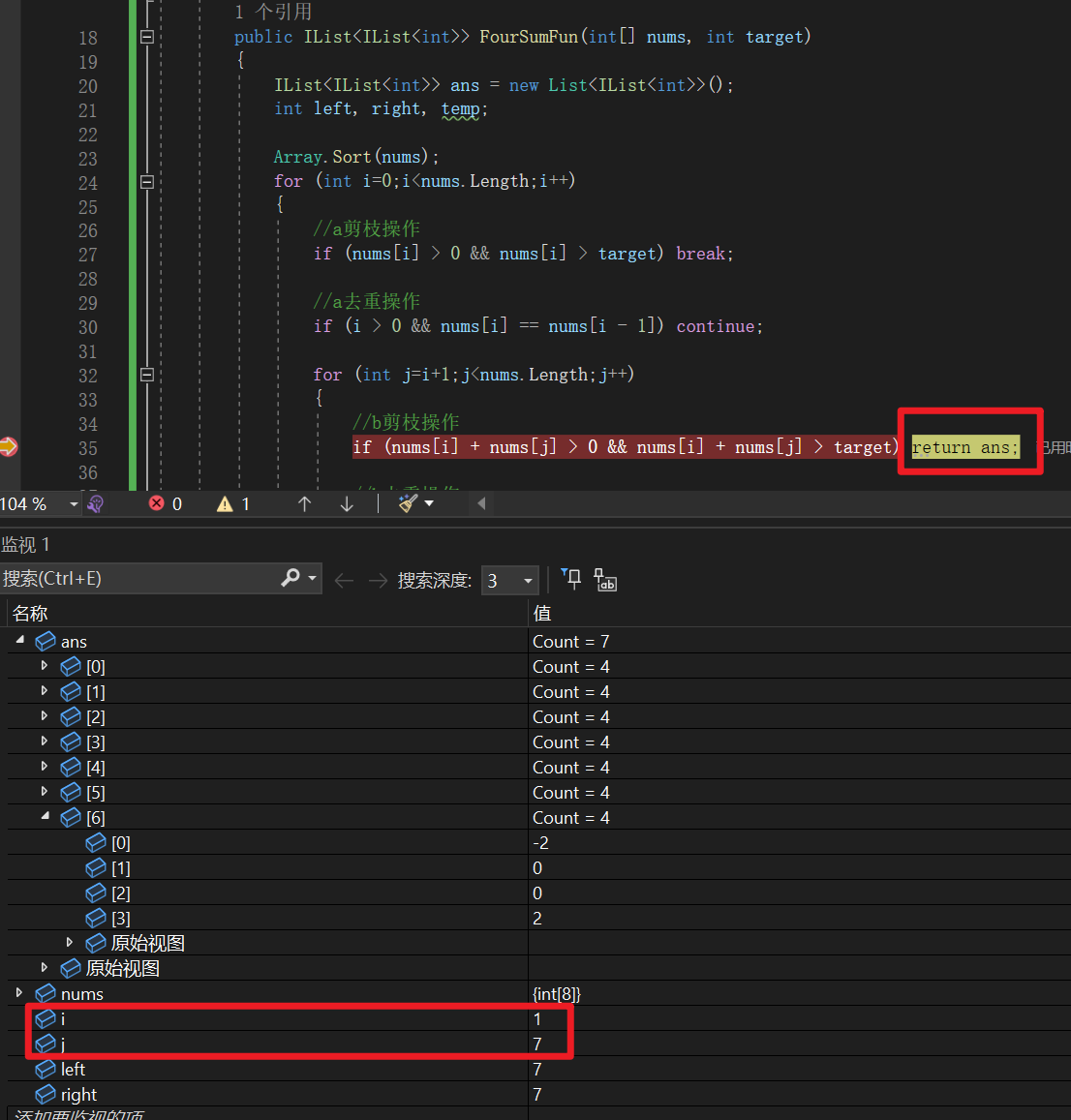
查看后发现，i和j下标对应的数组值相加后恰好大于target且他们也大于0。但是后续的-1 0 0 1也是一组答案，这里由于b剪枝的原因直接跳过了。这里就是问题所在。

代码实现

双指针法：

/// <summary>
/// 双指针法
/// </summary>
/// <param name="nums"></param>
/// <param name="target"></param>
/// <returns></returns>
public IList<IList<int>> FourSumFun(int[] nums, int target)
{
    IList<IList<int>> ans = new List<IList<int>>();
    int left, right;

    Array.Sort(nums);
    for (int i=0;i<nums.Length;i++)
    {
        //a剪枝操作
        if (nums[i] > 0 && nums[i] > target) break;

        //a去重操作
        if (i > 0 && nums[i] == nums[i - 1]) continue;

        for (int j=i+1;j<nums.Length;j++)
        {
            //b剪枝操作
            if (nums[i] + nums[j] > 0 && nums[i] + nums[j] > target) break;

            //b去重操作
            if (j > i + 1 && nums[j] == nums[j - 1]) continue;

            left = j + 1;
            right = nums.Length-1;

            while(left<right)
            {
                if (nums[i] + nums[j] + nums[left] + nums[right] == target)
                {
                    ans.Add(new List<int>() { nums[i], nums[j], nums[left], nums[right] });

                    left++;
                    right--;

                    //去重
                    while (left < right && nums[left] == nums[left - 1]) left++;

                    //去重
                    while (left < right && nums[right] == nums[right + 1]) right--;
                }
                else if (nums[i] + nums[j] + nums[left] + nums[right] < target)
                {
                    left++;
                }
                else
                {
                    right--;
                }
            }
        }
    }


    return ans;
}