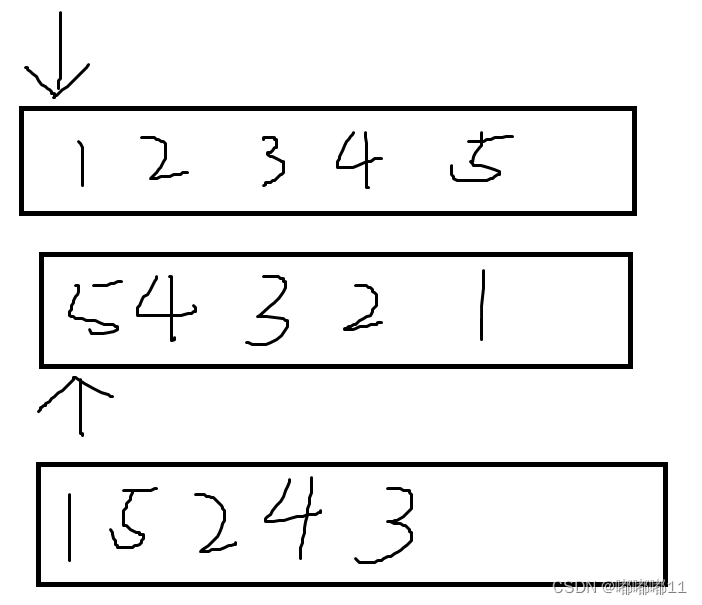
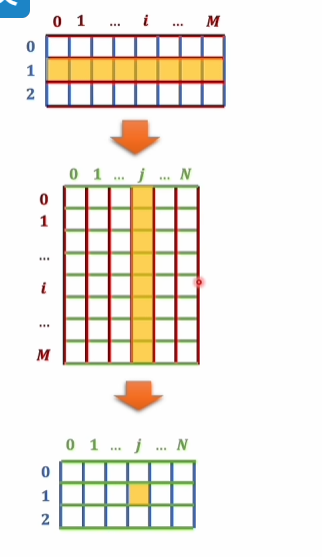
题目：

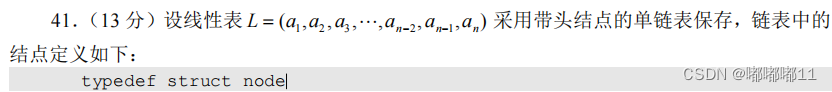
分析：要求空间复杂度为O（1），我们可以逆向假设可以开空间，得出一种思路，然后对这种思路优化空间即可得到O（1）

思路一：假设开空间

思考：再开一个空间倒着存链表的数据。开一个空间存储最终结果。对两条数据链依次遍历。上面选一个，下面选一个。惊奇的发现可以用两个指针代替开空间。开空间实际是对于下标的方便映射。两个指针是一样的效果。

思路二：双指针

思考：定义两个指针p，q。问题在于这两个指针该指向哪？如果是一个链表首，一个链表尾，链表尾的不能倒退。如果链表尾能倒退就好了。好思路！我们可以在遍历中将中间的后半段的next指针倒置，那么下次遍历的时候就可以倒退遍历了。q所指结点依次插入到p所指结点的后面。其中重点是怎么找到中间结点然后把后半段倒置，需要把两个指针停在中间结点和后一个结点。然后依次往后遍历。

#include <iostream>
#include <cmath>
using namespace std;

typedef struct node
{
	int data;
	struct node* next;
	//数据域整型，指向空	
}Node;//单个结点 
int n;
int create(node*  &L)
{
	node*t,*r;//临时指针和尾指针 
	r=L;
	cin>>n;
	for(int i=0;i<n;i++)
	{
		t=new node;
		scanf("%d",&t->data);
		t->next=NULL;
		r->next=t;
		r=t;
	}
	
}
void print(node* L)
{
	node*t;
	t=L->next;
	while(t!=NULL)
	{
		cout<<t->data<<' ';
		t=t->next;
	}
}

node* check(node* &L)
{
	node*p,*q;
	//求长度
	int len=0;
	p=L->next;
	while(p!=NULL)
	{
		len++;
		p=p->next;	
	} 
	
	//找到中间结点 
	p=L->next;
	int mid=len%2?len/2+1:len/2;
	for(int i=1;i<mid;i++) p=p->next;
	q=p->next;//下半段的第一个结点 
	
	node*t=p;//找一个结点替p指向NULL 
	while(q!=NULL)//后半段倒置 
	{
		node*T=q;//中间结点 
		q=q->next;
		T->next=p;
		p=T;
	}
	
	t->next=NULL;
	q=p;//将后半段的首结点给q
	p=L->next;//p指向前半段的首节点。
	
	//开始插入
	//这里用数值判断是因为上面的倒置处理让后半段多了一个元素 
	for(int i=1;i<=len-mid;i++) 
	{
		node*t=q;
		q=q->next;
		t->next=p->next;
		p->next=t;
		p=t->next;
	}
	return L;
}

int main()
{
	node* L;//单链表/头指针 
	L=new node;//创建单链表
	L->next=NULL; 
	create(L);//插入值 
	auto ans=check(L);
	print(L);
	return 0; 
}

时间复杂度：O（n），空间复杂度O（1） n为链表长度。

总结：这道题涉及的思路不难，难的是细节，因为处理中涉及到很多指针方向的转变，最好是一边画图一边把思路和代码写完整。要不然容易浪费很多时间。