📃博客主页: 小镇敲码人
💚代码仓库,欢迎访问
🚀 欢迎关注:👍点赞 👂🏽留言 😍收藏
🌏 任尔江湖满血骨,我自踏雪寻梅香。 万千浮云遮碧月,独傲天下百坚强。 男儿应有龙腾志,盖世一意转洪荒。 莫使此生无痕度,终归人间一捧黄。🍎🍎🍎
❤️ 什么?你问我答案,少年你看,下一个十年又来了 💞 💞 💞

【ZZULI数据结构实验】压缩与解码的钥匙:赫夫曼编码应用
- 🏆 实验目的和要求
- 🏆 实验前的准备工作
- 🔑 确定汉字编码
- 🔑 在文件中实现汉字的读和写
- 🍸 知道汉字的高位和低位在屏幕上打印汉字
- 👘 字符串形式(%s)打印
- 👘 字符形式(%c)打印
- 🍸 在文件中写入汉字(以GBK编码的形式)
- 🍸 在文件中读入中文,并以GBK编码的形式来输出
- 🏆 赫夫曼树的结构设计
- 🔑 知识点介绍
- 🔑 结构设计
- 🏆 赫夫曼树函数的具体实现
- 🔑 List_Init(链表初始化)和 Node_Init(节点初始化)
- 🔑 链表的销毁和赫夫曼树的销毁
- 🔑 链表的插入
- 🔑 buildHuffmanTree(构造赫夫曼树)
- 🔑 assignCodes(编码)
- 🍸 strdup函数介绍
- 🍸 编码函数实现
- 🔑 打印字符出现的频次
- 🔑 打印字符的编码
- 🏆 最终效果演示
- 🔑 菜单及调用函数实现
- 🔑 效果展示
前言:上篇博客,博主分享了多项式的运算实验,今天我们继续来看实验二——赫夫曼编码及应用。相关代码在博主的代码仓库自行查看。
🏆 实验目的和要求

🏆 实验前的准备工作
🔑 确定汉字编码
我们这次实验采用GBK编码来编码汉字,该编码标准兼容GB2312(ANSI),由两个字节来编码确定一个汉字,而且高位和低位为了和英文字符做区分,都是大于128的。我们可以看一下编码表。
- 也可以使用UTF-8编码,但是该编码会出现3个乃至4个字节编码一个汉字的情况,控制起来太复杂,所以我们不采用这个。
🔑 在文件中实现汉字的读和写
在学习如何在汉字中编码前,我们先来学习一下如何在屏幕上(标准输出流stdout)上打印一个用GBK编码的汉字。
🍸 知道汉字的高位和低位在屏幕上打印汉字
👘 字符串形式(%s)打印
我们通过查阅资料,知道了中文阿的高位和低位是0xB0、0xA2。
#include <stdio.h>
int main()
{
// 定义GBK编码的高位字节
int high = 0xB0;
// 定义GBK编码的低位字节
int low = 0xA2;
// 创建一个字符数组来存储GBK编码的汉字
unsigned char s[3] = { (unsigned char)high, (unsigned char)low, '\0' };
printf("%s", s);
return 0;
}
运行结果:
👘 字符形式(%c)打印
#include <stdio.h>
int main()
{
// 定义GBK编码的高位字节
int high = 0xB0;
// 定义GBK编码的低位字节
int low = 0xA2;
printf("%c%c",high,low);
return 0;
}
运行结果:
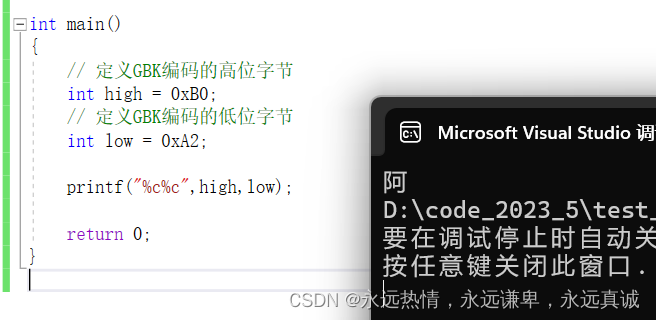
- 这里高位字节和低位字节用大小为1字节的类型也是可以的,但是要注意,应该使用
unsigned char无符号类型,这样就不会出现负数的情况(GBK编码高位和低位第一位都为1),便于我们的判断。的如果4字节的会发生截断。
🍸 在文件中写入汉字(以GBK编码的形式)
#include <stdio.h> // 引入标准输入输出库,用于文件操作和输入/输出函数
int main() // 主函数入口
{
// 声明一个文件指针pf,并尝试以写入("w")模式打开名为"诗.txt"的文件
FILE* pf = fopen("诗.txt", "w");
// 检查文件是否成功打开
if (NULL == pf)
{
// 如果文件打开失败,则输出错误信息(来自perror函数)
perror("fopen");
// 并返回错误代码1
return 1;
}
// 定义一个无符号字符数组s,用于存储用户输入的字符串,并初始化为全0
unsigned char s[600] = { 0 };
// 使用scanf函数从标准输入(通常是键盘)读取一个字符串,并存储在s中
// 注意:这里使用%s可能会引发缓冲区溢出问题,因为scanf不会检查目标数组的大小
// 更好的做法是使用fgets函数或者限制scanf读取的字符数
scanf("%s", s);
// 初始化一个循环计数器i,用于遍历字符串s
int i = 0;
// 循环遍历字符串s,直到遇到字符串结束符'\0'
while(s[i] != '\0')
{
// 声明两个无符号字符变量high和low,用于存储GBK编码的汉字的高位和低位字节
// 假设字符串s中包含GBK编码的汉字,但实际上这种假设可能不正确
unsigned char high = '\0';
unsigned char low = '\0';
// 将s中的当前字符赋值给high
high = s[i++];
// 如果high的值大于128(通常表示这是一个非ASCII字符),则假设它是GBK编码的汉字的高位字节
if(high > 128)
{
// 尝试将s中的下一个字符赋值给low(假设它是GBK编码的汉字的低位字节)
low = s[i++];
}
// 将high写入文件
fputc(high, pf);
// 如果low不为'\0'(即存在低位字节),则将其写入文件
if (low != '\0')
fputc(low, pf);
}
// 关闭文件
fclose(pf);
// 将文件指针设置为NULL,避免野指针
pf = NULL;
// 程序正常结束,返回0
return 0;
}
这是我们写入的内容:
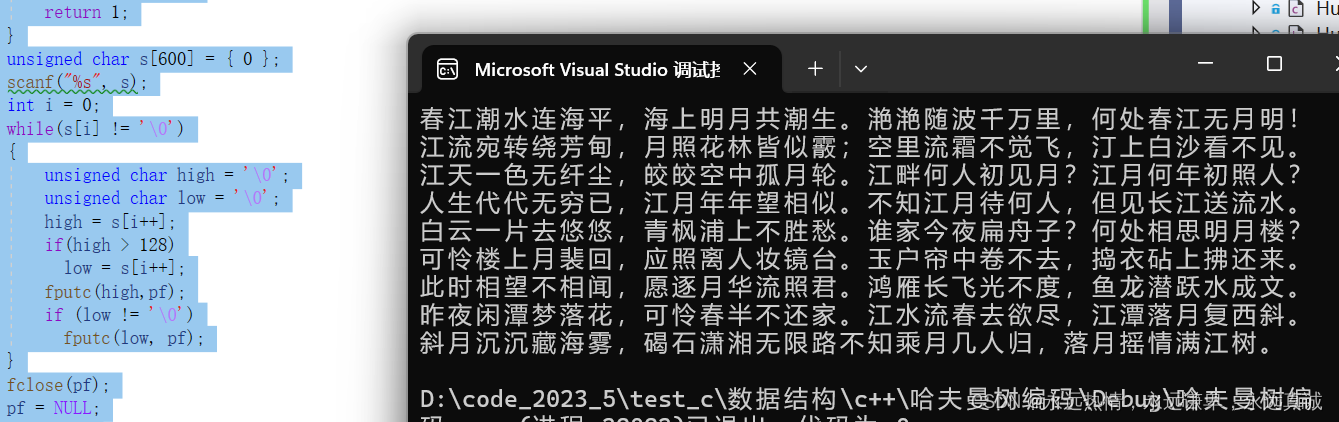
看看文件中是否生成了对应内容:
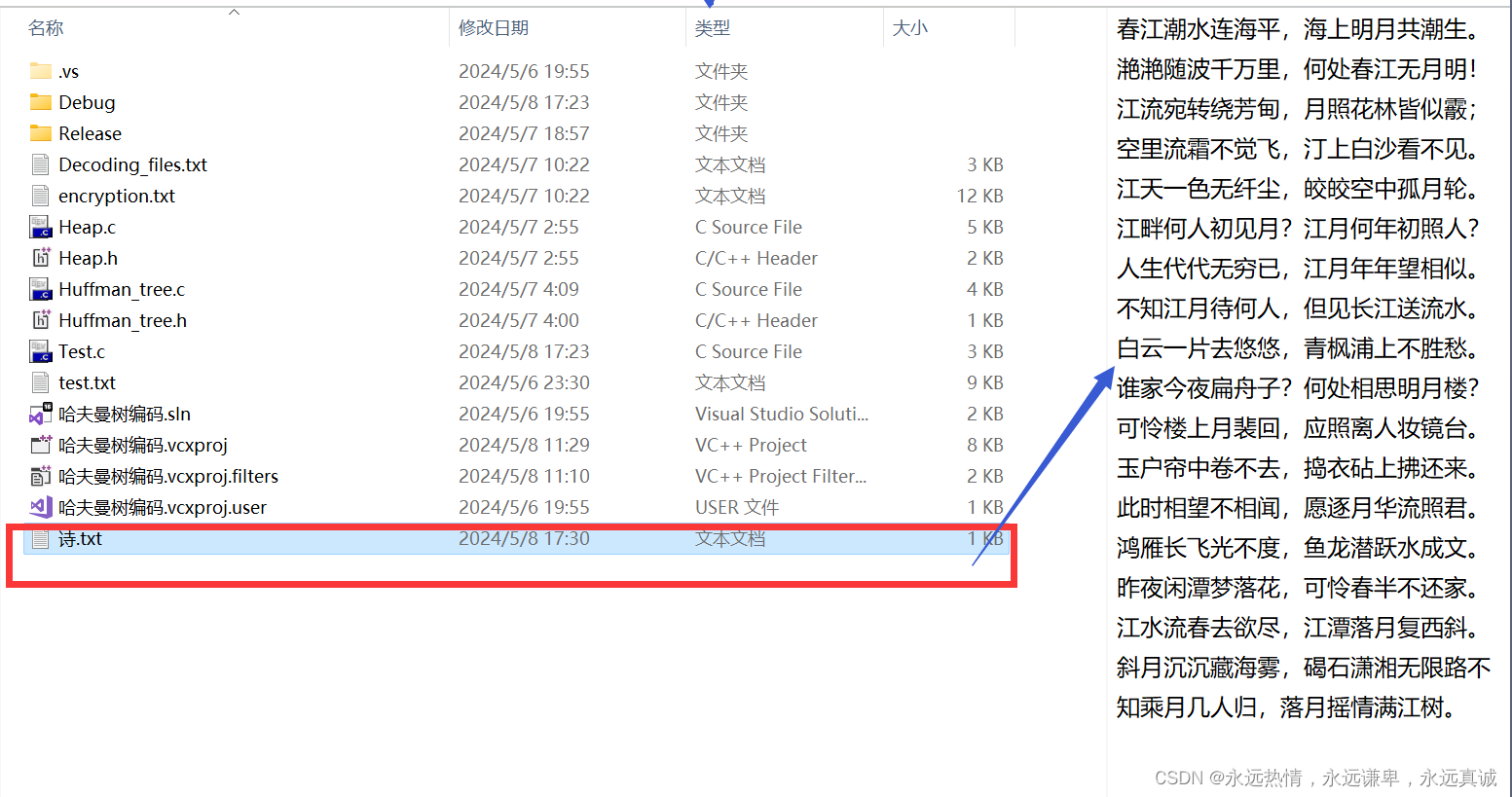
从右边的预览我们可以看见确实写入了对应的内容,有小伙伴可以会好奇,为什么换行了呢?我们刚刚我们明明没有换行呀,其实你如果点进这个文件会发现,其实并没有换行,只是预览这样可能更方便我们阅读:

🍸 在文件中读入中文,并以GBK编码的形式来输出
首先我们需要新建一个文件写入内容后,另存选择编码为GBK或者是它兼容的,因为程序编码格式和文件的编码格式必须保持一致。
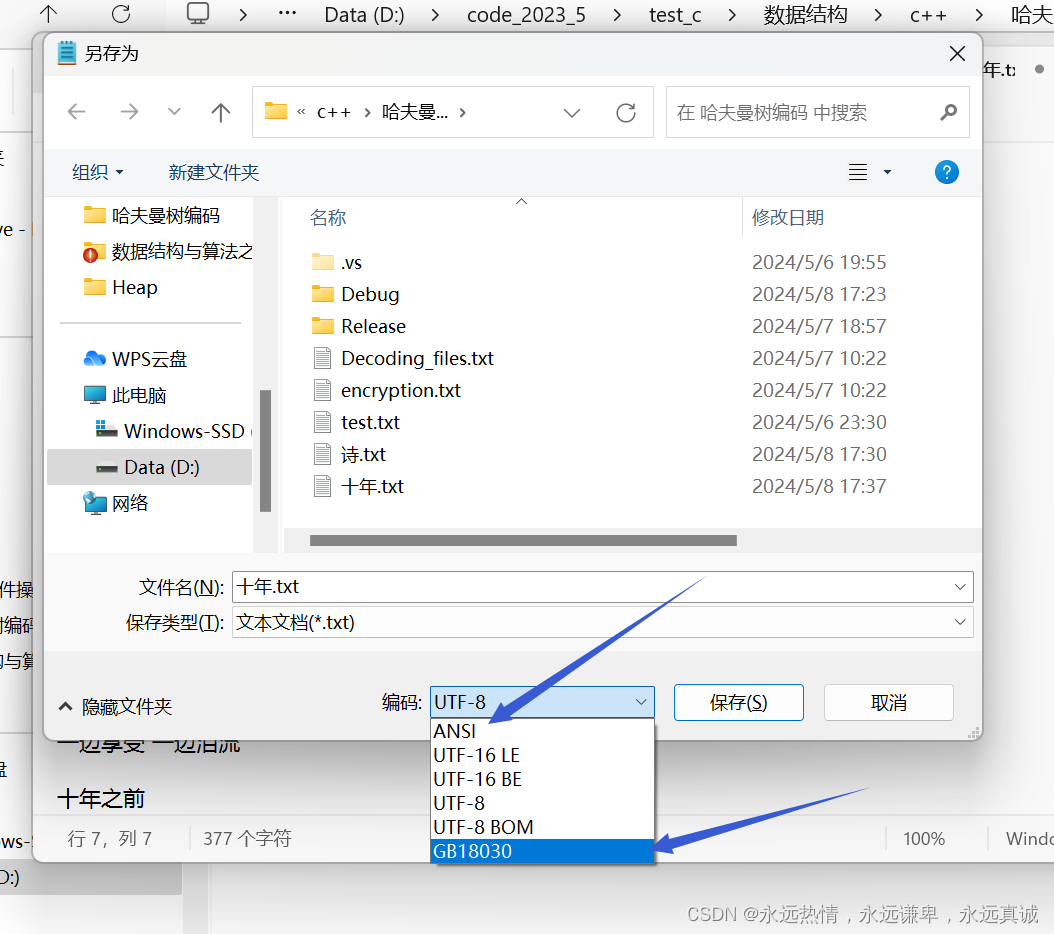
选择GB类型的编码或者ANSI都是,因为ANSI也是GB类型的一种,GBK都是兼容的他们的。这里我们选择ANSI编码。
文件中的内容如下:
下面我们用代码来以GBK的形式读一下文件中的内容并输出到屏幕上。
#include <stdio.h> // 引入标准输入输出库
int main()
{
// 声明一个文件指针pf,并尝试以只读("r")模式打开名为"十年.txt"的文件
FILE* pf = fopen("十年.txt", "r");
// 检查文件是否成功打开
if (NULL == pf)
{
// 如果文件打开失败,则输出错误信息
perror("fopen");
// 并返回错误代码1
return 1;
}
// 初始化两个变量high和low,high用于存储从文件中读取的字符,low用于存储汉字的低字节(如果存在)
int high = 0, low = '\0';
// 使用while循环从文件中逐个字符地读取,直到遇到文件结束符EOF
while ((high = fgetc(pf)) != EOF)
{
// 如果读取到的字符(存在于high中)大于128(假设是GBK或其他多字节编码的汉字的高字节)
if (high > 128)
{
// 读取下一个字符作为汉字的低字节(如果存在)
low = fgetc(pf);
// 输出高字节和低字节,但由于low可能不是汉字的低字节(例如遇到非汉字字符),
// 直接输出可能会导致乱码或不正确的输出。
printf("%c%c", high, low);
}
else
{
// 如果不是汉字的高字节,则只输出该字符
printf("%c", high);
}
}
// 关闭文件
fclose(pf);
// 将文件指针设置为NULL,避免野指针
pf = NULL;
// 程序正常结束,返回0
return 0;
}
运行结果:

这里还是用int来保存低位和高位较好,因为既要与128作比较来区分因为字符和中文字符,不能让系统把首位的1当作负号位,又要做判断文件结束的判断,因为EOF是-1,无符号数没有负数,所以如果使用无符号数,程序会陷入死循环。
所以接下来的实验中我们会以int类型保存字符的高位和低位。最终系统会发生截断的,所以我们不用担心int和char不匹配的问题。
🏆 赫夫曼树的结构设计
🔑 知识点介绍
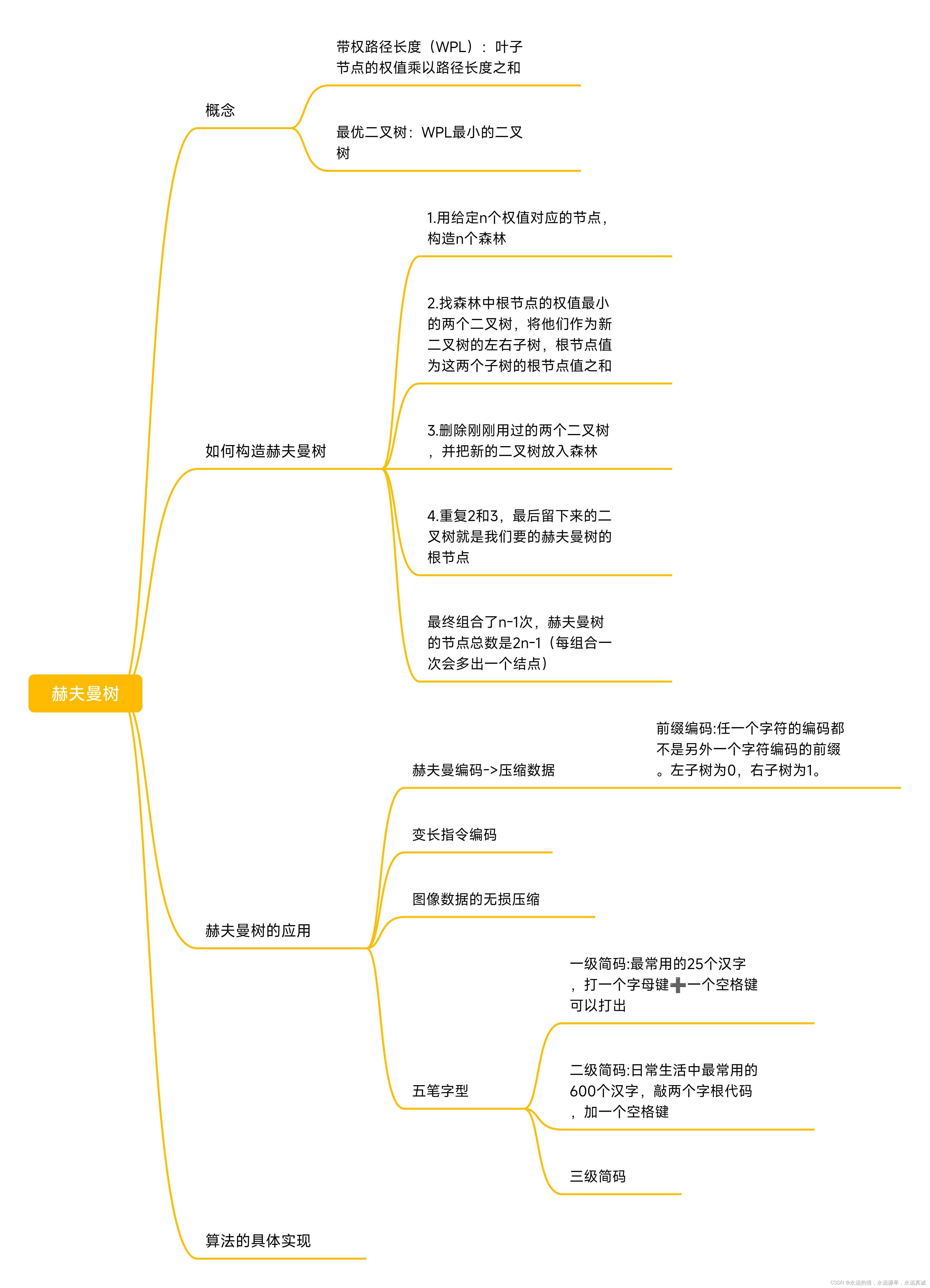
🔑 结构设计
赫夫曼树是一种特殊的二叉树,WPL最小的二叉树,所以赫夫曼树又叫最优二叉树。
首先就是哈夫曼树的节点类型,我们需要在这个类型里面放5个数据,节点的左孩子、右孩子、还有这个节点保存的字符即它的低位和高位,还有这个字符的字符串编码(char*类型,动态开辟内存按需申请)。
typedef struct HuffmanNode* NodeP;
typedef struct HuffmanNode {
unsigned int freq;//出现的频率
NodeP left, right;//节点的左孩子和右孩子
int low;//低位
int high;//高位
char* code; // 编码,在构造树后分配
}Node;
然后我们还需要一个线性表的结构,这个线性表用来保存每种字符的频率,可以使用链表或者线性表,这里我们使用的是链表。因为链表无需我们考虑申请空间的问题,省事很多。
typedef struct HuffmanList* ListP;//创建一个双向循环链表,存储节点的频度
typedef struct HuffmanList{
NodeP data;//哈夫曼树节点
ListP next;
}List;
这里我们把链表指针和树的节点指针类型取了一下别名,因为后面要多次使用,这样做可以少写一个*,指针的英文是Pointer,所以我们后面加了P代表这个是指针类型。
函数接口:
void List_insert(ListP Head,ListP newnode);//插入新的节点
ListP List_Init(NodeP data);//初始化链表
void Print_freq(ListP Head);//打印各个词出现的频率
void Destroy_List(ListP newnode);//销毁链表
NodeP Node_Init(int freq, int low, int high);//节点初始化
NodeP buildHuffmanTree(ListP* Head);//构造哈夫曼树
void assignCodes(NodeP root, char* code);//编码
void decode(NodeP root, FILE* encodedFile, FILE* decodedFile);//解码
void dfs(NodeP root);//前序遍历,打印节点和其对应的编码
🏆 赫夫曼树函数的具体实现
🔑 List_Init(链表初始化)和 Node_Init(节点初始化)
过于简单不过多叙述。
ListP List_Init(NodeP data)//链表节点初始化
{
ListP newL = (ListP)malloc(sizeof(List));//为链表节点申请空间
if (NULL == newL)
{
printf("malloc Failed\n");
exit(-1);
}
//初始化
newL->data = data;//初始化数据节点
newL->next = NULL;//初始化next为空
}
NodeP Node_Init(int freq, int low, int high)//赫夫曼树节点初始化
{
NodeP NewN = (NodeP)malloc(sizeof(Node));//为赫夫曼树节点申请空间
if (NULL == NewN)
{
printf("malloc Failed\n");
exit(-1);
}
//初始化
NewN->freq = freq;
NewN->high = high;
NewN->low = low;
NewN->left = NULL;
NewN->right = NULL;
NewN->code = NULL;
}
🔑 链表的销毁和赫夫曼树的销毁
- 注意:虽然链表里面存的有赫夫曼树的节点指针,但是节点的内存并不是和链表节点一起申请的,链表节点只是有一个4字节的变量也指向那片空间而以,而且链表里有的节点在赫夫曼树中肯定是存在的,节点的内存在赫夫曼树中走一个后序就可以释放,但是如果你在链表中就释放了,在释放赫夫曼树的时候,释放叶子节点时还需要特判一下,因为叶子节点已经释放过了(重复释放程序会崩溃),而且非法访问也会出问题,所以我们统一走后序在树中释放节点的内存。
void Destroy_List(ListP Head)
{
assert(Head);//断言,头节点不能为空
ListP Cur = Head;
while (Cur != NULL)
{
ListP next = Cur->next;
free(Cur);
Cur = next;
}
}
void Destroy_HuffmanTree(NodeP root)//销毁赫夫曼树
{
if (root == NULL)
return;
Destroy_HuffmanTree(root->left);//先去释放根节点的左树
Destroy_HuffmanTree(root->right);//再去释放根节点的右树
free(root);//最后释放根节点
}
🔑 链表的插入
链表的插入就是用来统计每个字符出现的频次的,具体逻辑是这样的,我们在外面的函数只需要传入字符的高位和低位即可,如果high和low已经出现了,就没有构造链表节点和赫夫曼树节点的必要,如果没有出现,外面就需要依次构造赫夫曼树节点和链表节点头插进链表中。
void List_insert(ListP Head,int high,int low)//插入节点
{
ListP cur = Head->next;
//循环遍历,看是否该字符已经存在
while (cur != NULL)
{
if (cur->data->high == high && cur->data->low == low)
{
cur->data->freq++;
break;
}
cur = cur->next;
}
if (cur == NULL)//没有找到,或者链表为空(只有一个头节点)
{
//构造新节点
NodeP newHnode = Node_Init(1,low, high);
ListP newLnode = List_Init(newHnode);
//头插进链表中
newLnode->next = Head->next;//先把Head后面的节点和新节点链接
Head->next = newLnode;//在把头节点的next更新
}
}
🔑 buildHuffmanTree(构造赫夫曼树)
统计完文件中每个字符的频次,我们得到对应的树节点,也可以将它们视作森林。因为此时它们还没有链接起来,因为每次我们需要依次取两个频次最小的节点,所以我们可以使用小堆(按照频次来调整)这种数据结构,一共有N个节点,每次调整只需要logN,调整N次,时间复杂度的量级在O(N * logN),我们来看排序一次排序是NlogN,有N次,大概在O(N logN* N)的量级。如果你直接找两个最小的,比排序还快一点N*N量级。如何构造我们不再详细赘述,在之前的思维导图中已经叙述过了。如果你对堆这种数据结构不太了解,可以看一下博主这篇博客。
NodeP buildHuffmanTree(ListP Head)//构造哈夫曼树
{
// 初始化最小堆,并将所有叶子节点加入堆中
Heap hp;
HeapInit(&hp);
ListP cur = Head->next;
while (cur != Head)
{
HeapPush(&hp, cur->data);
cur = cur->next;
}
//开始构造赫夫曼树
while (HeapSize(&hp) > 1) {
NodeP left = HeapTop(&hp);
HeapPop(&hp);
NodeP right = HeapTop(&hp);
HeapPop(&hp);
NodeP top = (NodeP)malloc(sizeof(Node));
top->freq = left->freq + right->freq;
top->left = left;
top->right = right;
top->high = -1;
top->low = -1;
top->code = NULL;
// 暂时不分配编码
HeapPush(&hp, top);//把新节点插入到堆中
}
// 堆中只剩一个节点,即根节点
NodeP root = HeapTop(&hp);
HeapDestory(&hp);
return root;
}
🔑 assignCodes(编码)
编码就是为叶子节点的code写入相应的字符编码,左孩子写字符0,右孩子写字符1,这是前缀编码模式,可以保证我们的每个叶子节点的编码都是唯一的,不存在二义性。我们先来隆重介绍一下一个非常棒的字符串函数strdup,如果你会使用这个函数,那简直是太酷了!
🍸 strdup函数介绍
这个函数主要做两件事,第一件事是拷贝字符串,第二件事是为这个字符串重新申请一片空间(在堆上),所以这个函数相当于是strcpy和malloc函数的结合,它拷贝的结束条件是\0,并且这个函数会给\0开一个空间。它会返回新开空间的起始地址。
- 如果我们给普通的字符指针的
\0位置赋值,是会报错的:
#include<stdio.h>
int main()
{
char* s = "11";
s[2] = '\0';
return 0;
}
运行结果:
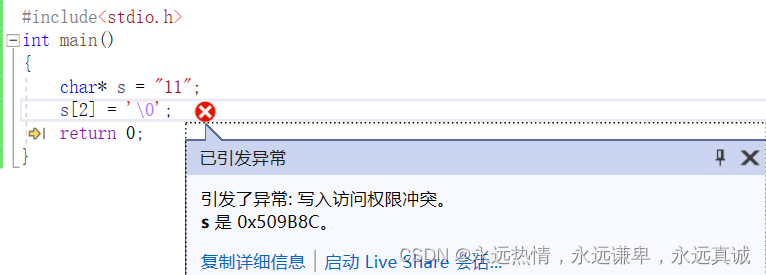
说我们非法访问了,但是字符串的结束标志不就是\0吗,如果你不把那一个字节的空间给我,该如何处理呢?这里我们先理解为是字符指针,系统会给它开这个空间但是不允许我们访问,这也算是一种保护机制,因为字符串是以\0来判断结束的,如果你随意更改,就会打印乱码。
- 如果我们把这个相同的字符串给
_strdup函数,执行同样的操作,系统不会报错但是打印出来会乱码。
#include<stdio.h>
int main()
{
char* s = _strdup("11");
s[2] = '2';
printf("%s", s);
return 0;
}
运行结果:

这是因为我们把原先的\0给修改了,这个函数变相的给了我们控制字符指针\0的权利,有好处也有坏处。
- 将
strcat和strdup函数结合,恢复字符串特性(以\0)结尾。
因为strcat函数会把源字符串的\0也拷贝进去,如果你不懂字符串拼接函数strcat,可以看一下博主这篇博客,这里正常应该会报错因为那个字节的空间,并不是我们的。我们暂且认为这里是特殊处理,但是博主发现这个函数还是存在很大的不确定性,所以实际项目里面还是老老实实的使用malloc和循环去计算字符串长度。
#include<stdio.h>
int main()
{
char* s = _strdup("11");
strcat(s, "1");
printf("%s", s);
return 0;
}
运行结果:

不再出现乱码。
🍸 编码函数实现
void assignCodes(NodeP root, char* code)//编码
{
if (root == NULL) return;
if (root->left == NULL && root->right == NULL) {
// 叶子节点,分配编码
root->code = _strdup(code);
}
else {
// 递归为左树和右树上的叶子节点分配编码
assignCodes(root->left, strcat(_strdup(code),"0"));
assignCodes(root->right, strcat(_strdup(code),"1"));
}
}
🔑 打印字符出现的频次
// 打印各个词及其出现频度的函数
// 参数:
// ListP Head - 指向链表头部的指针,链表中的每个节点存储了一个词及其相关信息
void Print_freq(ListP Head) // 打印各个词出现的频度
{
assert(Head);//Head不能为空
// cur 是一个临时指针,用于遍历链表
ListP cur = Head->next; // 从链表的第一个有效节点开始遍历(假设Head是头节点,不存储数据)
// 当cur不为空时,说明还有节点未遍历
while (cur != NULL)
{
// 检查当前节点的数据(词)是否有'low'属性(可能是指多字符的词或某种特殊标识)
if (cur->data->low == -1)
{
// 如果'low'为-1,说明只有一个字符(可能是单字符词或特殊标识),直接打印该字符和它的频度
char c = cur->data->high;
if (c == '\n' || c == '\r')
printf("\\n\\r: %d次\n", cur->data->freq);
else
printf("%c: %d次\n", cur->data->high, cur->data->freq);
}
else
{
// 如果'low'不为-1,说明是多字符的词,打印两个字符(或特殊标识)和它的频度
printf("%c%c: %d次\n", cur->data->high, cur->data->low, cur->data->freq);
}
// 移动到下一个节点
cur = cur->next;
}
}
🔑 打印字符的编码
// 深度优先搜索函数,用于遍历树结构
// 参数:
// NodeP root - 指向树节点的指针,该节点是遍历的起始点
void dfs(NodeP root)
{
// 如果当前节点为空(到达叶子节点的下一层或根节点之前就是空的),则直接返回
if (!root)
return;
// 如果当前节点是叶子节点(即没有左孩子和右孩子)
if (root->left == NULL && root->right == NULL)
{
// 检查节点是否有'low'属性(可能是某种辅助信息或键值)
if (root->low == -1)
{
// 如果'low'为-1,说明只有一个字符(可能是单字符词或特殊标识),直接打印该字符和它的频度
char c = root->high;
if (c == '\n' || c == '\r')//换行符特殊处理
printf("\\n\\r: %s\n",root->code);
else
printf("%c: %s\n", root->high, root->code);
}
// 如果'low'不是-1(即存在'low'属性),则按照指定格式打印
else
printf("%c%c: %s\n", root->high, root->low, root->code);
}
// 递归遍历左子树
dfs(root->left);
// 递归遍历右子树
dfs(root->right);
}
🏆 最终效果演示
🔑 菜单及调用函数实现
#define _CRT_SECURE_NO_WARNINGS 1
#include"Huffman_tree.h"
char file[200] = { 0 };//存储原始文件路径
ListP Head = NULL;//链表头指针
NodeP root = NULL;//赫夫曼树的根节点指针
void Test1()//完成统计字符频次的事情
{
FILE* pf = fopen(file, "r");//打开原始文件
if (NULL == pf)//如果打开失败
{
perror("fopen");
return 1;
}
int high = 0;
int low = -1;
Head = List_Init(NULL);//带头单链表,创建它的头
while ((high = fgetc(pf)) != EOF)//开始读取文件的内容
{
if (high > 128)//如果是中文字符
low = fgetc(pf);
List_insert(Head,high,low);
low = -1;//注意要及时置为-1,因为有时候不是中文字符
}
}
void Test2()//完成打印字符频次表的工作
{
assert(Head != NULL);//Head不能为空
Print_freq(Head);
}
void Test3()//完成构建赫夫曼树,并打印每个字符对应的01编码的工作
{
assert(Head != NULL);//Head不能为空
root = buildHuffmanTree(Head);
assignCodes(root, "");//编码
dfs(root);//遍历打印
}
void Test4()//完成写入加密文件并打印加密文件的路径的工作
{
assert(Head != NULL);//Head不能为空
assert(root != NULL);//root不能为空,保证已经加密过了
FILE* pf = fopen(file, "r");//打开原始文件
if (NULL == pf)
{
perror("fopen");
return 1;
}
FILE* pfw = fopen("encryption.txt", "w");//创建加密文件,相对路径
if (NULL == pfw)
{
perror("fopen");
return 1;
}
int high = -1, low = -1;
while ((high = fgetc(pf)) != EOF)//读取文件字符
{
if (high > 128)//判断中文字符
{
low = fgetc(pf);
}
ListP cur = NULL;
cur = Head->next;
while (cur != NULL)//依次在表中找对应的字符并写入它的编码
{
if (cur->data->high == high && cur->data->low == low)
{
fputs(cur->data->code, pfw);
break;
}
cur = cur->next;
}
low = -1;//防止中文字符对英文字符产生干扰
}
printf("加密文件的路径为:D:\\code_2023_5\\test_c\\数据结构\\c++\\哈夫曼树编码\\encryption.txt\n");//打印加密文件路径,这个是自己事先就确定的
//关闭对应的文件
fclose(pfw);
fclose(pf);
pfw = NULL;
pf = NULL;
}
void Test5()//完成解密的工作,并打印解密的路径
{
assert(root != NULL);//root不为空
FILE* pfw = fopen("encryption.txt", "r");//打开加密的文件
if (NULL == pfw)
{
perror("fopen");
return 1;
}
FILE* pfD = fopen("Decoding_files.txt", "w");//创建解密文件
if (NULL == pfD)
{
perror("fopen");
return 1;
}
decode(root, pfw, pfD);//调用解密函数
printf("解密文件的路径为:D:\\code_2023_5\\test_c\\数据结构\\c++\\哈夫曼树编码\\encryption.txt\n");//打印解密文件的绝对路径
//关闭文件
fclose(pfw);
fclose(pfD);
pfw = NULL;
pfD = NULL;
}
void Test6()//完成清理资源的操作
{
Destroy_HuffmanTree(root);//清理赫夫曼树中的资源
root = NULL;
Destroy_List(Head);//清理链表中的资源
Head = NULL;
printf("清理资源成功<>\n");
}
void menu()//菜单函数
{
int instructions = 0;
printf("请输入指令以执行操作<>\n: ");
printf("***********************************************************************************************************\n");
printf("****************************1.输入要加密的文件路径(绝对路径和相对路径均可)*******************************\n");
printf("****************************2.打印字符频次表***************************************************************\n");
printf("****************************3.打印字符编码*****************************************************************\n");
printf("****************************4.输出加密01文件路径***********************************************************\n");
printf("****************************5.输出解码文件路径*************************************************************\n");
printf("****************************6.清理相关资源*****************************************************************\n");
printf("****************************7.刷新屏幕*********************************************************************\n");
printf("****************************8.结束程序*********************************************************************\n");
scanf("%d", &instructions);
switch(instructions)
{
case 1: { printf("请输入要加密的文件路径<>:\n"); scanf("%199s", file); Test1(); }
break;
case 2: Test2();
break;
case 3: Test3();
break;
case 4: Test4();
break;
case 5: Test5();
break;
case 6: Test6();
break;
case 7: system("cls");
break;
case 8: exit(0);
break;
default: printf("指令不合法,重新输入\n");
break;
}
}
int main()
{
while (1)//循环打印菜单
{
menu();
}
return 0;
}
🔑 效果展示
- 代码运行结果:
词频及字符串编码打印:

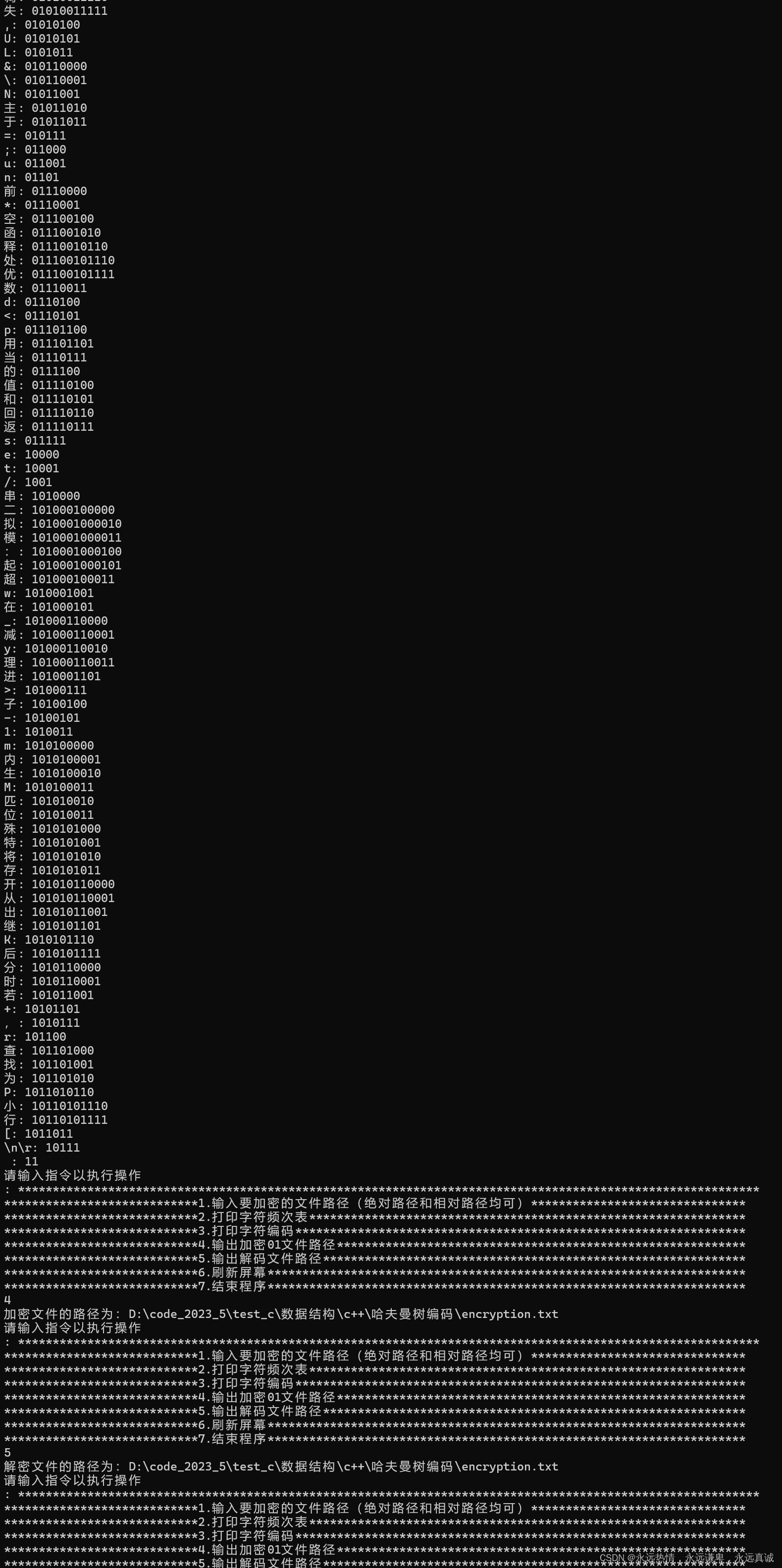
- 加密01字符串文件
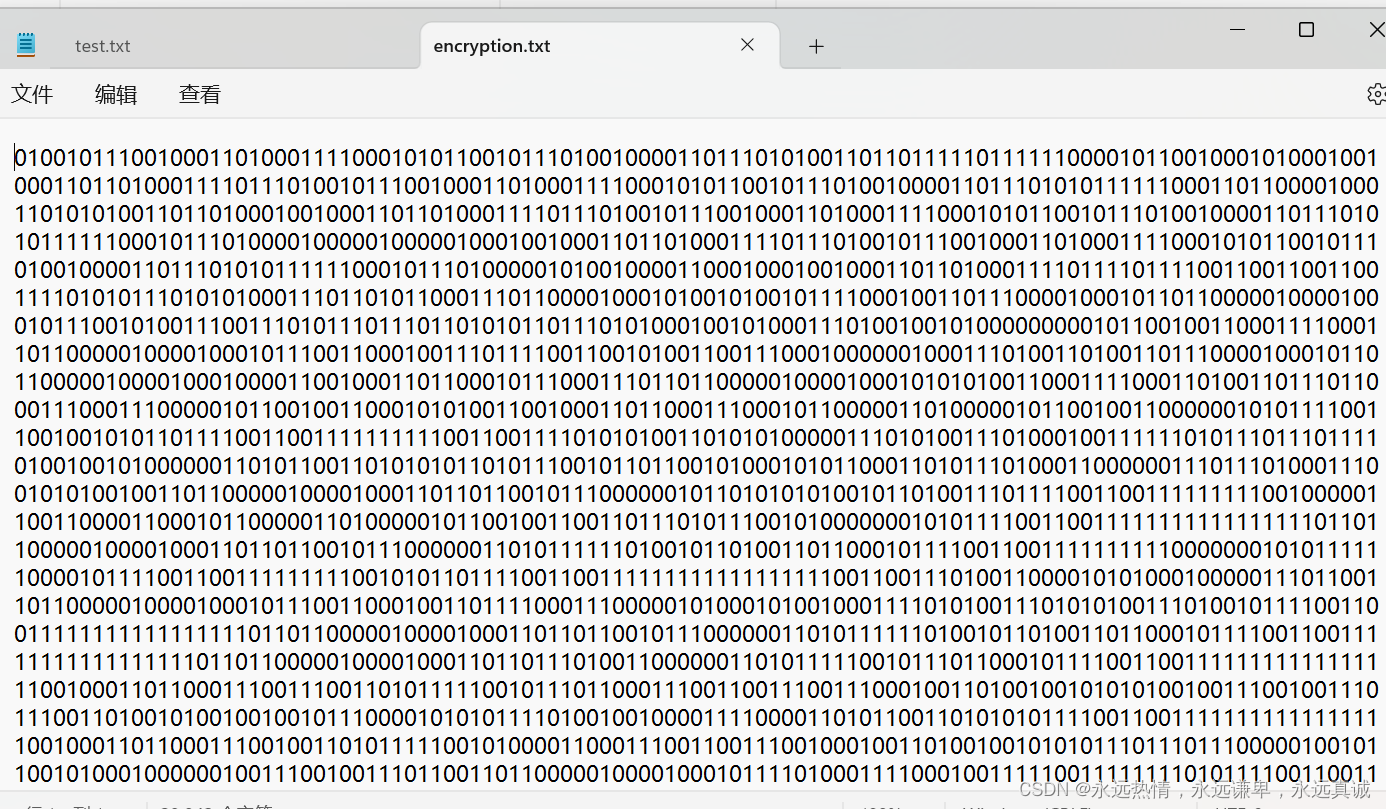
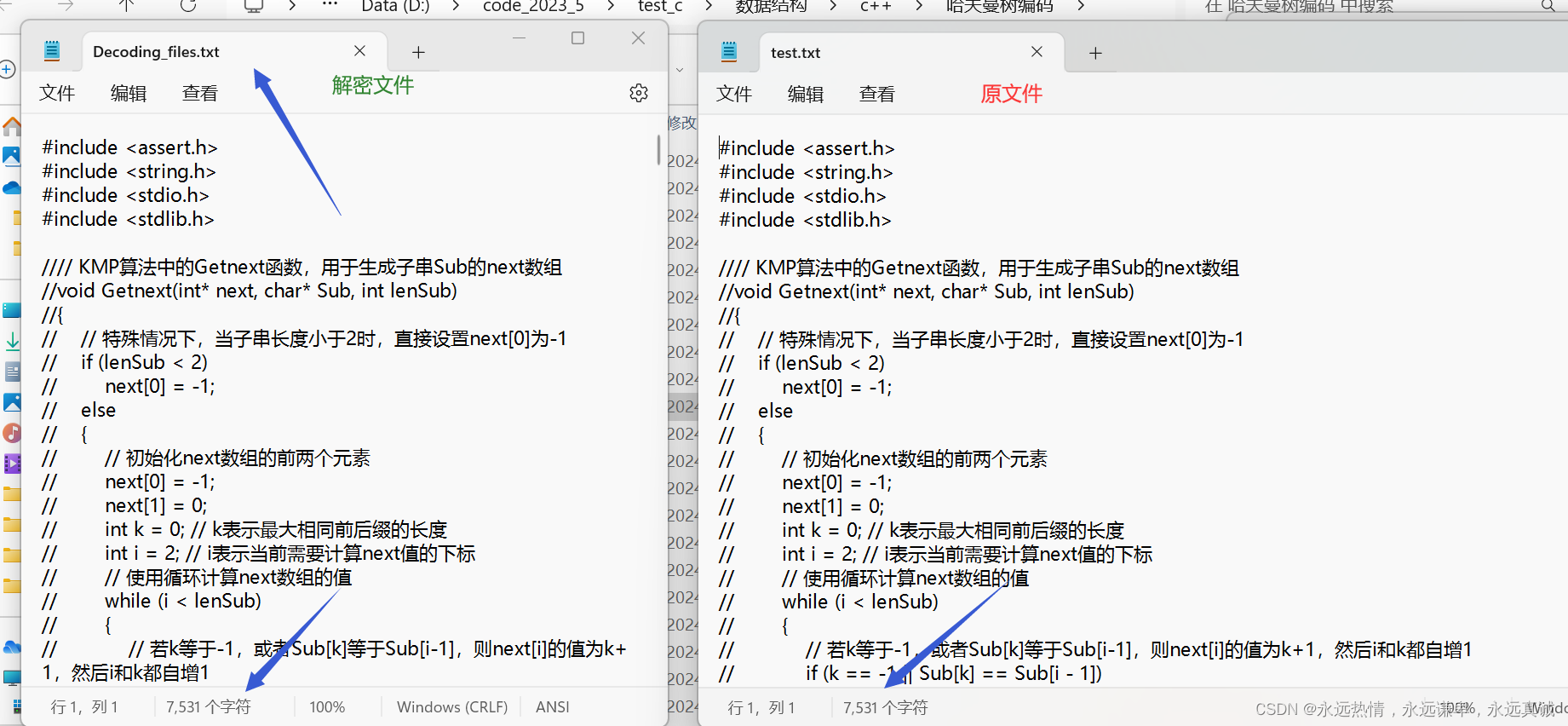
3. 解密文件与原文件对比结果。






![Python中批量提取[]括号内第一个元素的四种方法](https://img-blog.csdnimg.cn/direct/b4ac8fe970da4c6c92ff1b60a01c0124.png)