目录
思维训练
走方格
解题思路
参考代码
最短曼哈顿距离
编辑 解题思路
参考代码
酒厂选址
解题思路
参考代码
雪地足迹Tracks in the Snow
解题思路
参考代码
一个星期没有更博客了…这一个星期,去学校信竞集训的我收获颇丰,下面就是我的还加集训总结
思维训练
下面是思维训练中比较重要的题目
走方格
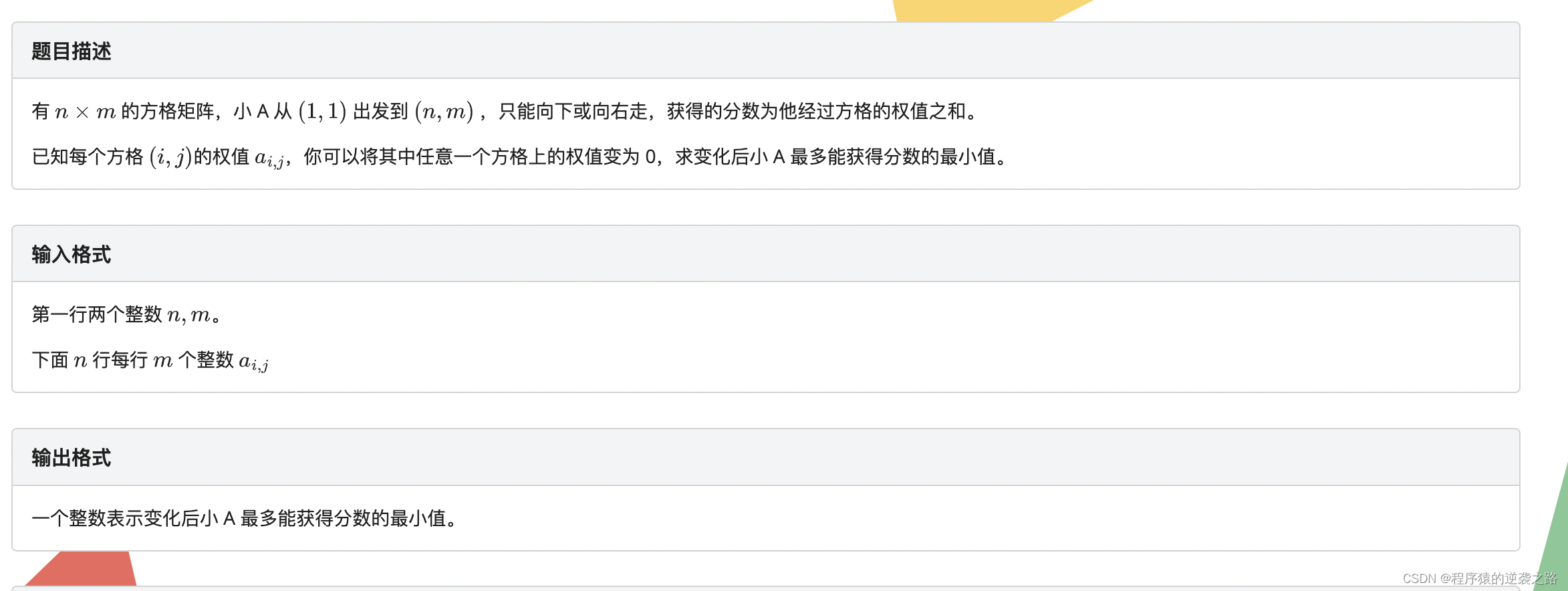
解题思路
本题主要考查了动态规划;
我们用dp1[i][j]记录从(1,1)到(i,j)的最大得分
我们用dp2[i][j]记录从(i,j)到(1,1)的最大得分
由于要经过点(i,j),但是要去掉(i,j)的最大得分
如下图:
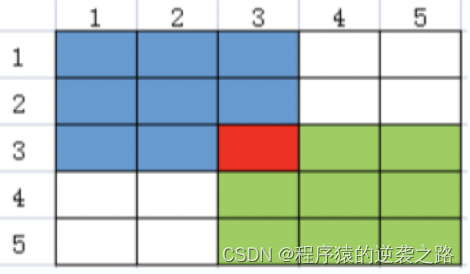
从左侧绕开(i,j)的最大得分
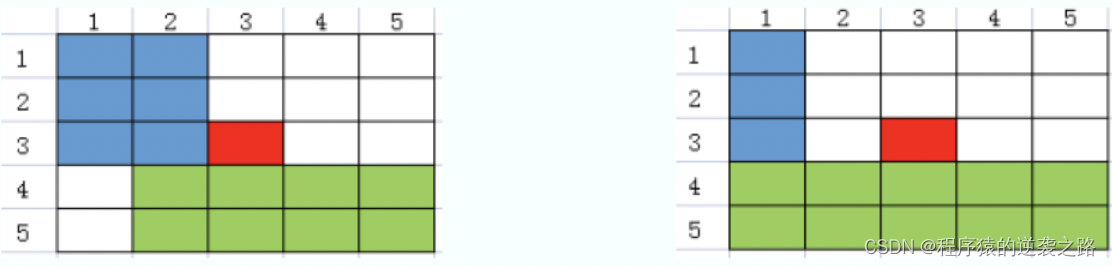
从上方绕开(i,j)的最大得分

所以最多能获得的最小值为
参考代码
#include<bits/stdc++.h>
using namespace std;
long long n,m,dp2[2005][2005];
long long dp1[2005][2005];
long long a[2005][2005];
long long x[2005][2005];
long long y[2005][2005];
long long minn=LONG_LONG_MAX;
int main(){
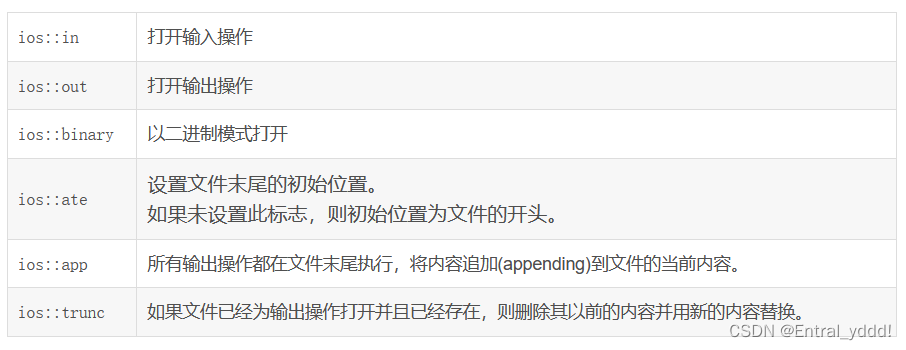
ios::sync_with_stdio(false);
cin>>n>>m;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>a[i][j];
dp1[i][j]=max(dp1[i-1][j],dp1[i][j-1])+a[i][j];
}
}
for(int i=n;i>=1;i--){
for(int j=m;j>=1;j--){
dp2[i][j]=max(dp2[i+1][j],dp2[i][j+1])+a[i][j];
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
x[i][j]=max(x[i][j-1],dp1[i][j-1]+dp2[i+1][j-1]);
y[i][j]=max(y[i-1][j],dp1[i-1][j]+dp2[i-1][j+1]);
minn=min(minn,max(max(x[i][j],y[i][j]),dp1[i][j]+dp2[i][j]-a[i][j]*2));
}
}
cout<<minn<<endl;
return 0;
}最短曼哈顿距离

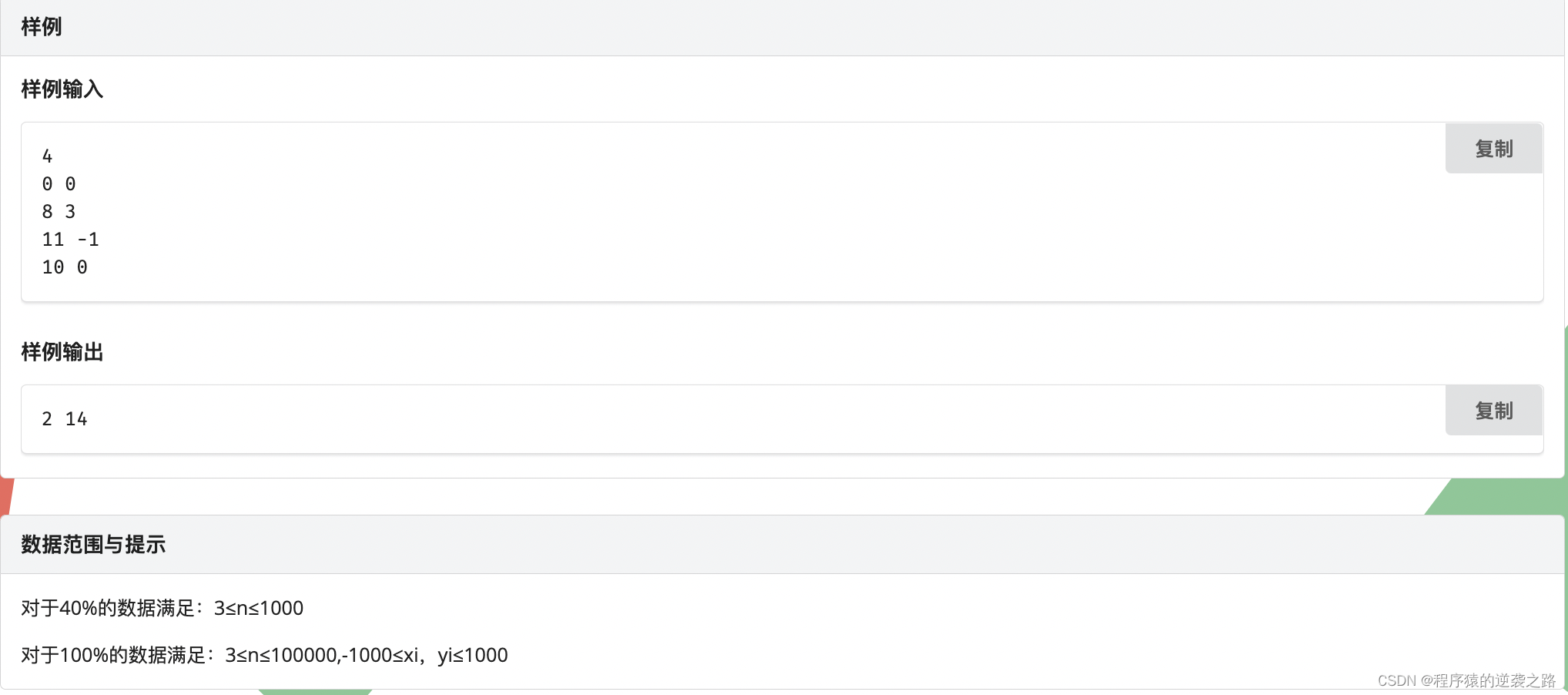 解题思路
解题思路
题意是按照顺序一次去掉一个点后的最短曼哈顿距离,所以每个店需要记录其与相邻两个点的距离和离起点的距离,所以要定义二维数组,因为对于100%的数据满足3≤n≤100000,-1000≤xi,yi≤1000,所以储存所有点的坐标有一点浪费,于是我就用的滚动数组来存储最近三个点的坐标.就可以计算出每一个点的三种距离,滚动数组的下标用%3来区分每个点与之相邻两个点的坐标.
去掉某个点,需要修改新的总距离,例如去掉一号点,会有以下的改变.
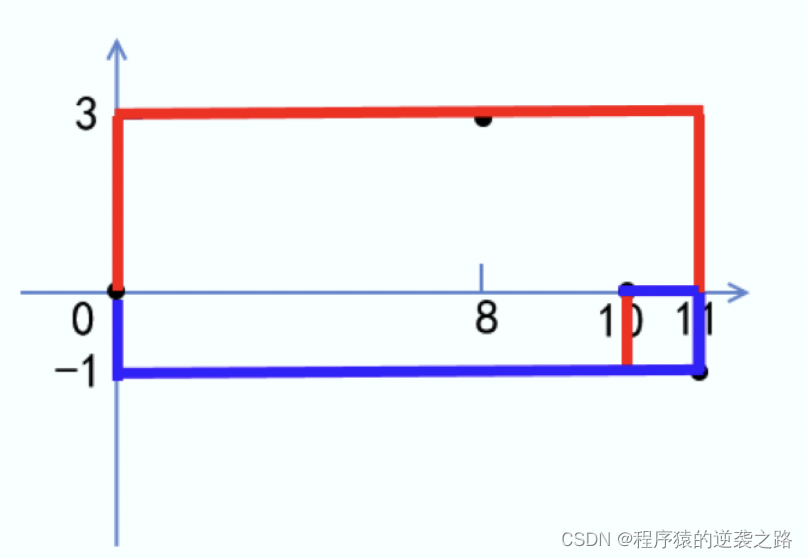
参考代码
#include<bits/stdc++.h>
using namespace std;
const int MAX=100005;
long long a[MAX][3],map1[3][2];
long long pos,n,sum,tot,tmp;
int f(int x,int y,int px,int py){
return fabs(x-px)+fabs(y-py);
}
int main(void){
ios::sync_with_stdio(false);
cin>>n>>map1[0][0]>>map1[0][1];
cin>>map1[1][0]>>map1[1][1];
a[1][0]=a[1][1]=a[1][2]=f(0,0,map1[1][0],map1[1][1]);
for(int i=2;i<n;i++){
cin>>map1[i%3][0]>>map1[i%3][1];
a[i][1]=f(map1[(i-1)%3][0],map1[(i-1)%3][1],map1[i%3][0],map1[i%3][1]);
a[i][2]=f(map1[(i-2)%3][0],map1[(i-2)%3][1],map1[i%3][0],map1[i%3][1]);
a[i][0]=a[i-1][0]+a[i][1];
}
sum=tot=a[n-1][0];
for(int i=1;i<n-1;i++){
tmp=tot+a[i+1][2]-a[i][1]-a[i+1][1];
if(tmp<=sum)pos=i,sum=tmp;
}
cout<<pos+1<<" "<<sum<<endl;
return 0;
}
酒厂选址

解题思路
本题主要考查了前缀和and枚举的思想.我用的d[i]记录从1号店到i号点的距离,sum来累加总距离,有余数据是一个单环,所以任意两点之间的距离有两种情况
或
选择较小的距离来计算运算成本.由于可能有多个消费相同最大的城市,所以每一个点都要枚举讨论,在这个点修建酒厂是否代价最小.
参考代码
#include<bits/stdc++.h>
using namespace std;
const int MAX=100005;
long long a[MAX],b[MAX],n;
long long tmp,ans,minn=LONG_LONG_MAX;
int main(){
ios::sync_with_stdio(false);
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i-1]>>b[i];
ans+=b[i];
b[i]=b[i]+b[i-1];
}
for(int i=0;i<n;i++){
tmp=0;
for(int j=0;j<n;j++){
if(fabs(b[j]-b[i])<=ans/2){
if(j!=i){
tmp+=fabs(b[j]-b[i])*a[j];
}
}else if(fabs(b[j]-b[i])>ans/2){
if(j!=i){
tmp+=(ans-fabs(b[j]-b[i]))*a[j];
}
}
}
minn=min(minn,tmp);
}
cout<<minn<<endl;
return 0;
}
雪地足迹Tracks in the Snow
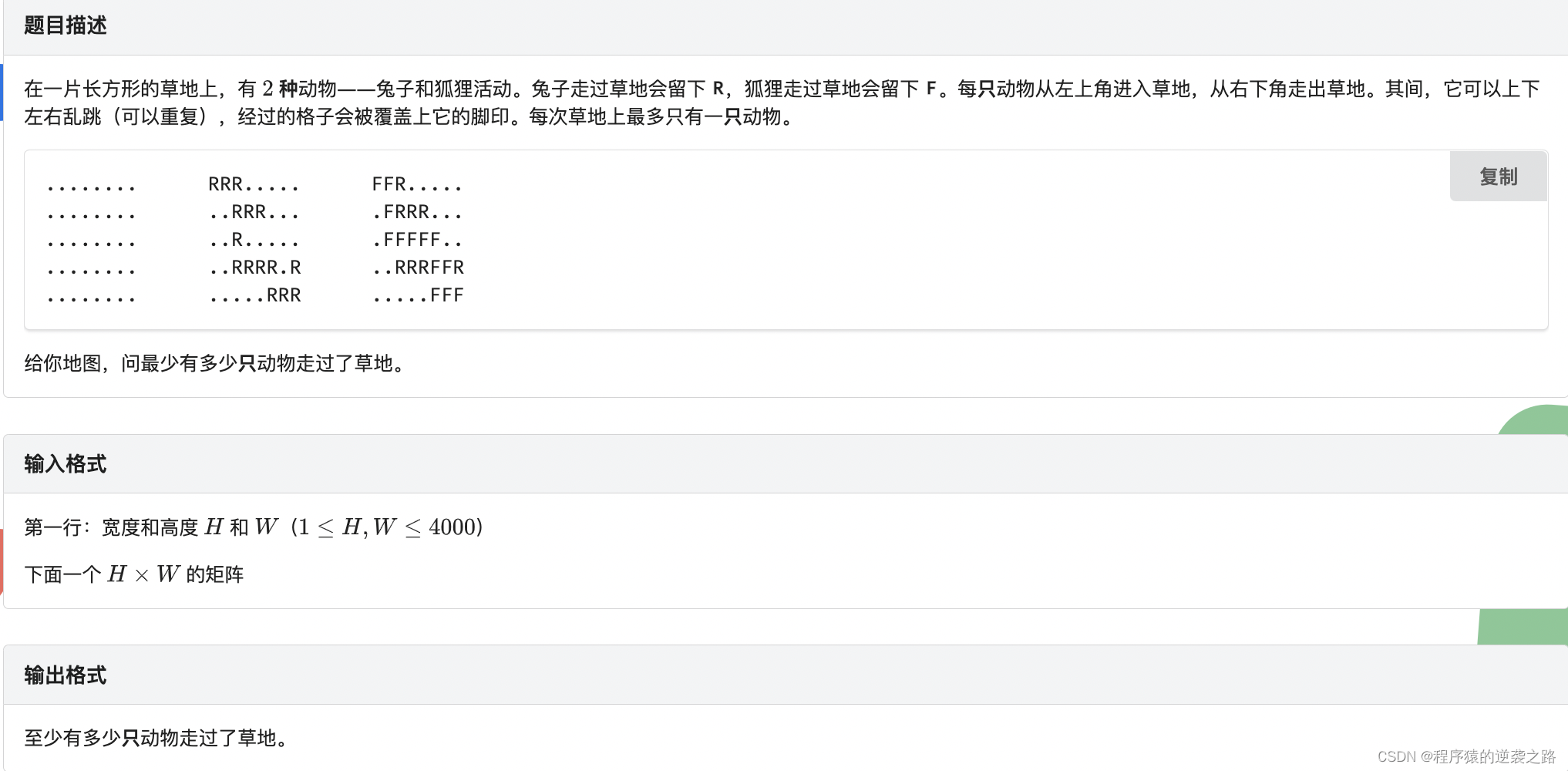
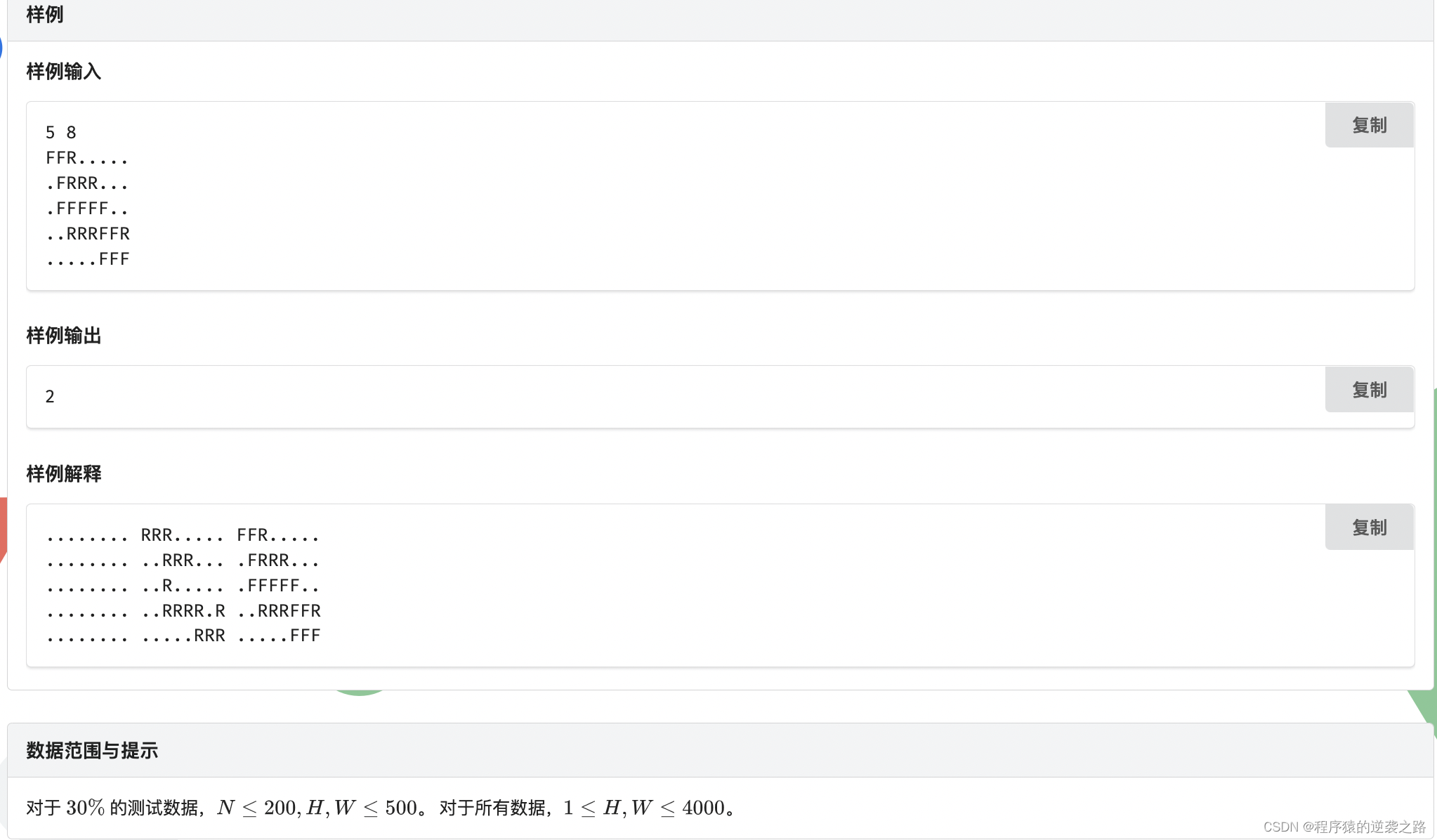
解题思路
本题我主要是用deque(双端队列)做的,当搜索到不同的动物的时候,我就用pair来记录这个动物出现的下标,(1,1)坐标是最后一种动物,注意不会出现连续着相同的动物进入草坪,因为这样踩的脚印只能由第一个动物去完成.把当前位置的相邻动物入队:相同的动物放队头,不同的动物放队尾.并且记录目前已经出队的动物种类,如果队头对应的动物和之前的动物不同,说明就有新的动物出现,cnt+1;
参考代码
#include <bits/stdc++.h>
using namespace std;
const int M=4005;
char mp[M][M];
int fx[4][2]={-1,0,0,1,1,0,0,-1};
int h,w,cnt;
char sum,last;
typedef pair<int,int> pr;
deque<pr> q;
int main(){
ios::sync_with_stdio(false);
scanf("%d%d",&h,&w);
for(int i=1;i<=h;i++)
scanf("%s",mp[i]+1);
last=char('R'+'F'-mp[1][1]);
q.push_front(pr(1,1));
while(!q.empty()){
pr now=q.front();
q.pop_front();
sum=mp[now.first][now.second];
if(sum==0)continue;
mp[now.first][now.second]=0;
if(sum!=last){
last=sum;
cnt++;
}
for(int i=0;i<4;i++){
pr pos=pr(now.first+fx[i][0],now.second+fx[i][1]);
char next=mp[pos.first][pos.second];
if(next==sum) q.push_front(pos);
else if(next+sum=='R'+'F') q.push_back(pos);
}
}
printf("%d\n",cnt);
return 0;
}这个是寒假集训总结的第一篇文章,所有的文章都在我的专栏里面保存着的.