本专栏主要记录力扣的刷题记录,备战蓝桥杯,供复盘和优化算法使用,也希望给大家带来帮助,博主是算法小白,希望各位大佬不要见笑,今天要分享的是——《507.完美数、509. 斐波那契数、520. 检测大写字母》。
目录
507.完美数
题目描述
解题思路
解题过程
509. 斐波那契数
题目描述
解题思路
解题代码
520. 检测大写字母
题目描述
解题思路
解题代码
507.完美数
题目描述
对于一个 正整数,如果它和除了它自身以外的所有 正因子 之和相等,我们称它为 「完美数」。
给定一个 整数
n, 如果是完美数,返回true;否则返回false。示例 1:
输入:num = 28 输出:true 解释:28 = 1 + 2 + 4 + 7 + 14 1, 2, 4, 7, 和 14 是 28 的所有正因子。示例 2:
输入:num = 7 输出:false
解题思路
首先求因子想到的是暴力循环,两个列表去遍历,但看到通过率我就知道这题暴力循环肯定会超出时间限制,先试一试:
解题过程
def checkPerfectNumber(num):
fin_list = []
for i in range(num):
for j in range(num+1):
if i * j == num:
fin_list.append(i)
if sum(fin_list) == num:
return True
else:
return False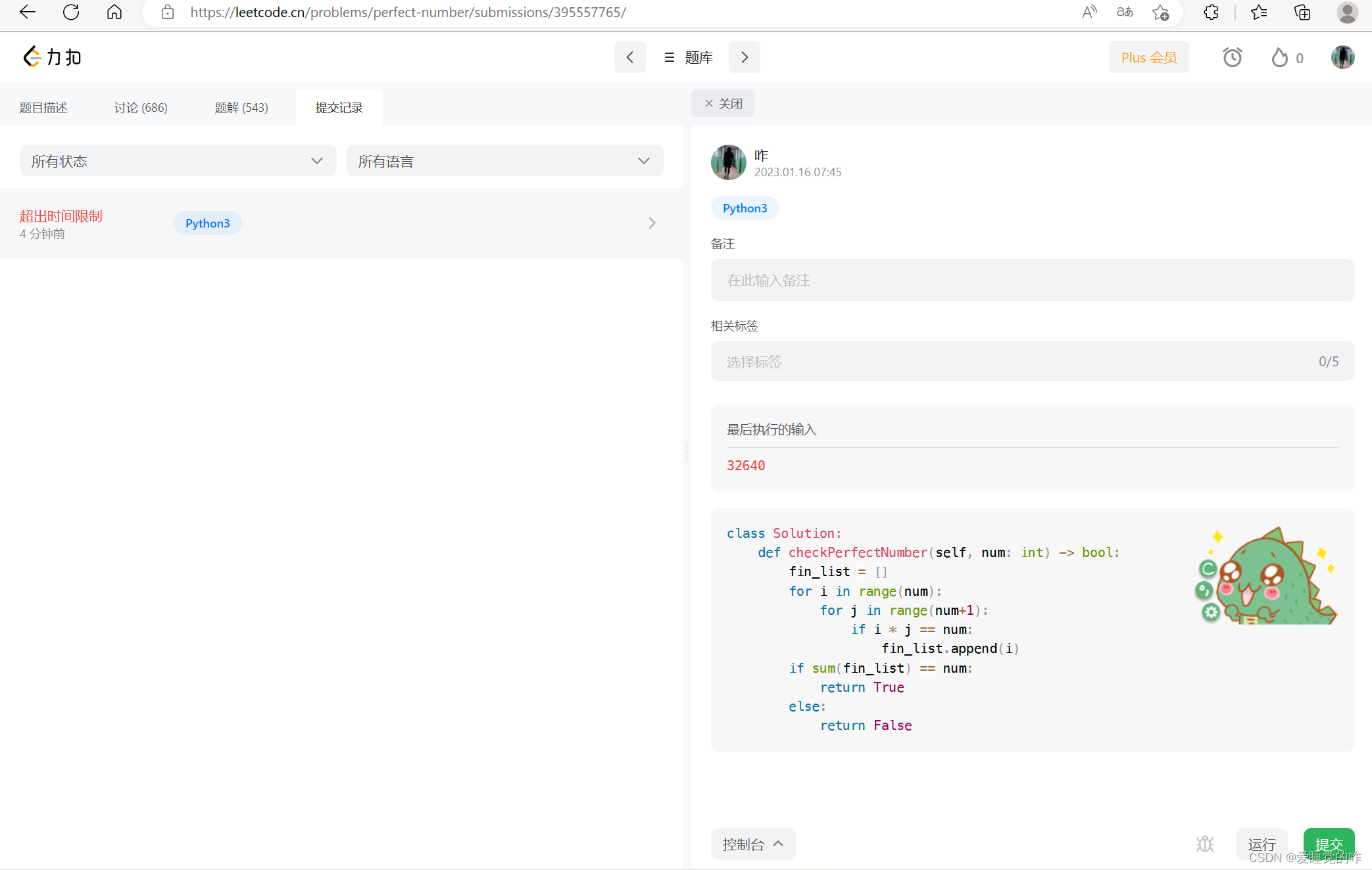
果然,超出了时间限制,看来得降低时间复杂度。实际上我们只需要判断2-int(math.sqrt(num))+1就可以了,添加的时候也不要用列表添加了,改成数字相加,这样能大大优化时间复杂度。
def checkPerfectNumber(num):
target = 1
# 只需要判断2-sqrt(num)+1
if num == 1:
return False
for i in range(2,int(math.sqrt(num))+1):
if num%i == 0:
target += i
target += num//i
if target == num:
return True
else:
return False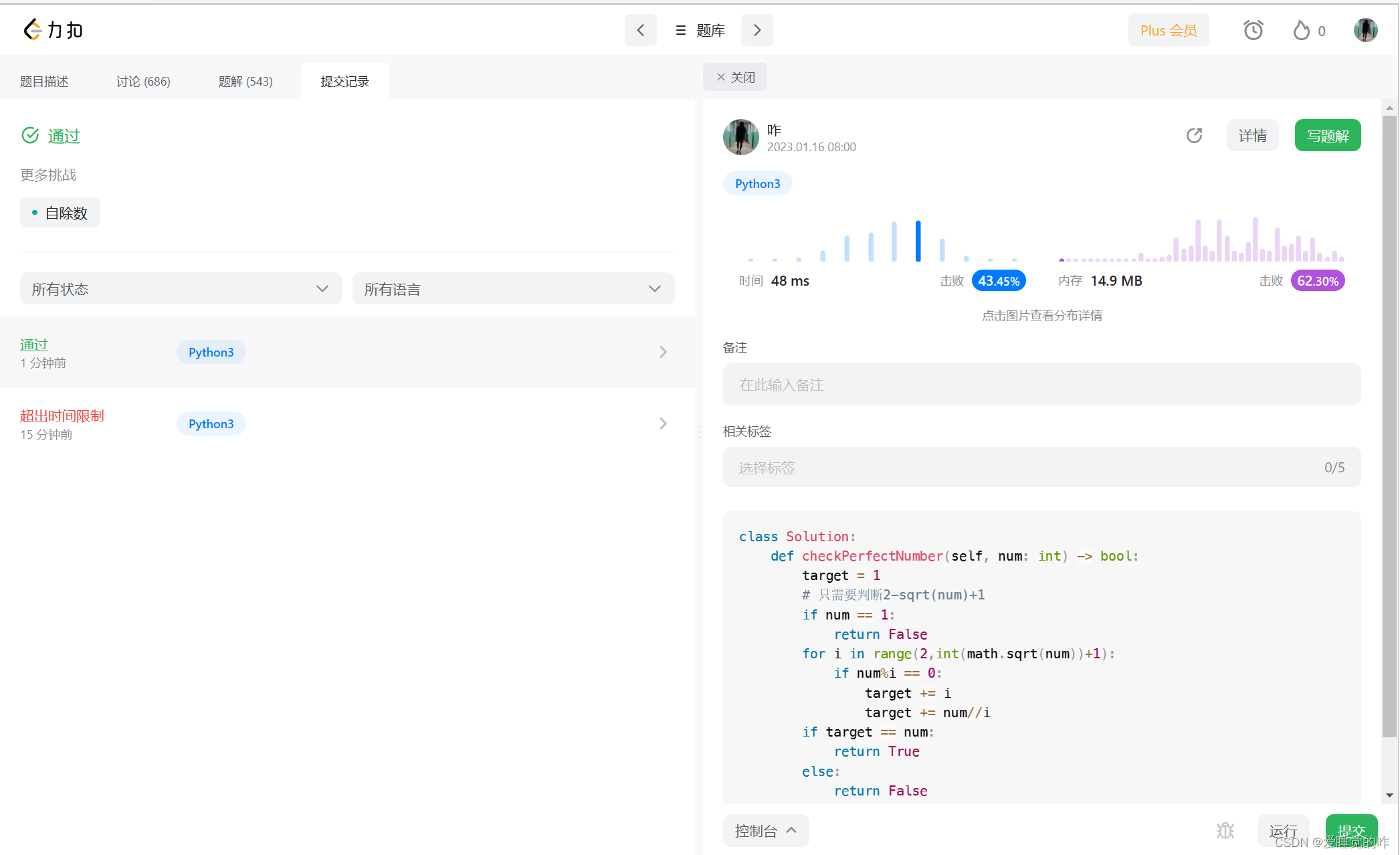
509. 斐波那契数
题目描述
斐波那契数 (通常用
F(n)表示)形成的序列称为 斐波那契数列 。该数列由0和1开始,后面的每一项数字都是前面两项数字的和。也就是:F(0) = 0,F(1) = 1 F(n) = F(n - 1) + F(n - 2),其中 n > 1给定
n,请计算F(n)。示例 1:
输入:n = 2 输出:1 解释:F(2) = F(1) + F(0) = 1 + 0 = 1示例 2:
输入:n = 3 输出:2 解释:F(3) = F(2) + F(1) = 1 + 1 = 2示例 3:
输入:n = 4 输出:3 解释:F(4) = F(3) + F(2) = 2 + 1 = 3
解题思路
这题就是很典型的斐波那契递归问题,用递归能够很好的解决问题。
解题代码
def fib(n):
if n == 0:
return 0
elif n ==1:
return 1
else:
return fib(n-1) + fib(n-2)
520. 检测大写字母
题目描述
我们定义,在以下情况时,单词的大写用法是正确的:
- 全部字母都是大写,比如
"USA"。- 单词中所有字母都不是大写,比如
"leetcode"。- 如果单词不只含有一个字母,只有首字母大写, 比如
"Google"。给你一个字符串
word。如果大写用法正确,返回true;否则,返回false。示例 1:
输入:word = "USA" 输出:true示例 2:
输入:word = "FlaG" 输出:false
解题思路
将符合要求的情况转化为大写字母,好在python字符串提供了相应的API,直接调用就可以,内存和速度表现的都很不错。
解题代码
def detectCapitalUse(word:str):
if word.isupper() or word.islower() or word.title() == word:
return True
else:
return False