碎碎念:小编去年数学建模比赛的时候真的理解不了主成分分析中的“主成分”的概念!!但是,时隔两年,在机器学习领域我又行了,终于搞明白了!且看正文!再分享一个今天听到的播客中非常触动我的一句话吧:“人生也许没有诗和远方,你脚下的苟且就是你没有发现的诗和远方。”来自钱婧老师的新书《我有自己的宇宙》
第一次更新:2024/5/10
目录
一. 引入
1. 为什么要降维
2. 如何降维
二. PCA(Principal Component Analysis)主成分分析
1. 主要思想
1.1 相关性理解
1.2 特征空间重构
1.3 主成分
2. 数学建模
2.1 最大投影方差
2.2 最小重构代价
3. 算法原理
4. matlab代码
一. 引入
1. 为什么要降维
数据的维度增高在机器学习中会带来“维度灾难”:高维度数据(如大型矩阵或稠密向量)可能会占用大量存储空间,并且计算复杂性和时间可能会随着维度的增加而急剧增加。这可能导致计算资源和存储空间的瓶颈,从而影响算法性能和系统效率。同时,高维数据也会带来数据稀疏,怎么理解这个稀疏呢?
假设我们有一个全世界总人口的数据集,如果我们按照性别这个特征关注数据,会发现此时数据是稠密并且相对均匀分布的;如果我们加入年龄、学历又会发现,此时的数据相对原来有一点点稀疏;如果再加入性格、身高、外貌等多个维度的特征时会发现满足这些特征的数据只有你一个,这个维度下的数据当然是稀疏的。
所以为了提高我们处理数据的模型的性能,降低计算的复杂度我们就会用到“降维”这个手段了。
2. 如何降维
我们常见的降维手段主要包括三类:特征降维、线性降维、非线性降维。
- 特征降维主要思想就是人为或者机器来筛选我们需要的特征,将不需要的特征变量删除;
- 线性降维是最常用的降维手段,主要包括PCA主成分降维和多维缩放降维;
- 非线性降维主要思想是主要思想是利用非线性映射将原始数据从原始空间映射到一个低维空间,主要包括IsoMAP、LLE算法等。
二. PCA(Principal Component Analysis)主成分分析
1. 主要思想
先来搜一下常见定义:
主成分分析(PCA:Principal Component Analysis)旨在通过正交变换将可能存在相关性的变量转换为一组线性不相关的变量,即主成分。PCA的核心是数据降维思想,通过降维手段实现多指标向综合指标的转化,使得转化后的综合指标(主成分)之间互不相关,并且尽可能地保留原始数据集的信息。
但看这一段是不是很懵?我也很懵,咱别看它,开始我们的正文。
我们知道一个数据集的如果特征较多的话就可能导致某些特征之间是存在相关性的,降维的一个切入点就可以是尽量让可以代表一类特征的一个变量来代替很多变量,进一步可以设想达到我们降维后的变量之间的相关性非常小,这样就说明我们降维后的变量是“有代表性的”。在数学中如何刻画这种相关性呢?我们分为几何角度和代数角度:
1.1 相关性理解
几何角度
我们先来看一个二维特征空间:
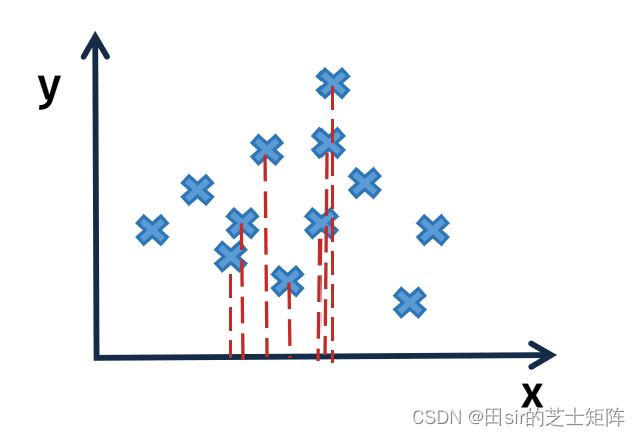
我们发现在x轴上数据呈现出明显的“拥挤”现象,即特征变量的相关性较高在几何上通常表现为线条的聚集或重叠。这意味着多个特征变量在图形上表现出较为接近的分布,它们的线条有时会交叉或重叠。这表明这些变量之间存在较高的相关关系,即一个变量的变化往往伴随着另一个变量的相应变化。
代数角度
数据在某一方向上的“拥挤”在数学上可以理解为在这个方向上数据的波动性较小(总体方差较小)。当特征变量之间高度相关时,在数据集中不同的特征变量波动方向和大小通常相近,因此总体方差相对较小。
同时高度相关的特征变量之间可能存在多重共线性问题,即它们之间存在相互依赖的关系。这可能导致方差解释性的降低,因为多重共线性的存在可能会混淆变量之间的因果关系。
1.2 特征空间重构
我们在原有的方向上特征重合度较高,主成分分析给予我们一个思路:换个角度看
如果旋转一下坐标系,使得在新坐标系下不同特征“分得很开”,会更有利于我们理解数据:

当我们在新的坐标系再观察数据时会发现,从
的方向上看数据已经相对不再那么“拥挤”了,此时数据在
方向上的离散程度最大,即方差最大。
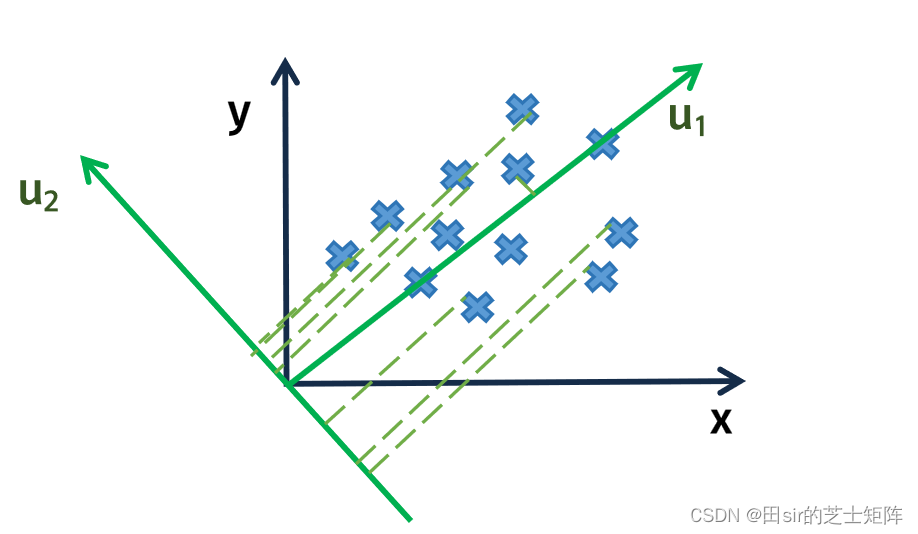
与此同时在轴上的方差较小。
所构建的新的特征空间简化了系统结构。
1.3 主成分
在主成分分析中,主成分指的是数据方差最大的方向,即数据在某一方向上的变化。
在我们的二维例子中,方向的方差最大,也就是第一主成分;其次,
为第二主成分。
在高维坐标系下我们做的工作也只是构建一个特征空间,按照每个坐标轴(也就是该特征空间下的基)方向的方差大小排序,就可以得到第一、第二、第三...主成分了。
通过将原始数据投影到主成分的坐标系中,我们可以减少数据的维度,同时保留原始数据中的大部分信息。主成分分析的目标是找到数据的主成分,这些主成分能够最大限度地保留原始数据的方差,同时尽可能减少彼此之间的相关性。
在主成分分析中,第一个主成分通常包含原始数据集中的大部分信息,因为它对应于数据的主要变化方向。后续的主成分通常包含的数据信息逐渐减少,因为它们更多地反映原始数据中的冗余或重复信息。
2. 数学建模
主成分分析的核心数学原理借鉴b站博主的又红又专的总结:一个中心,两个基本点
- 一个中心:对原始特征空间的重构,将相关特征转化为无关特征
- 两个基本点:(1)最大投影方差 (2)最小重构代价
机器学习-白板推导系列(五)-降维(Dimensionality Reduction)_哔哩哔哩_bilibili
在主要思想板块我们详细讲了特征空间的重构,这里就不过多赘述了,下面我们来手推两个基本点
2.1 最大投影方差
前提:
数据中心化:
向量长度: 即

数学模型:
结论:
主成分方向就是特征值λ的最大特征向量方向
2.2 最小重构代价

数学模型:
结论:
前q个主成分最大的方向就是协方差阵的前q个特征向量
3. 算法原理
基本的算法思路如下:
- 数据标准化:在PCA之前,所有数据都应该标准化(归一化)。这是由于PCA通过线性变换对特征进行降维,所以任何具有非零均值的特征都可能被误导。
- 计算协方差矩阵:PCA基于协方差矩阵对数据进行降维。在这个过程中,我们假设所有变量之间都存在某种相关性。
- 计算协方差矩阵的特征向量和特征值:协方差矩阵的特征向量表示了数据的主要变化方向,而特征值的平方根表示了每个方向上的方差贡献。
- 选择主成分:选择前k个主成分,其中k是我们要降到的维度数。通常会选择那些特征值占总特征值之和的95%以上的主成分。
- 应用主成分:对于原始数据中的每个样本,我们可以通过将其投影到选定的主成分上,从而将其降维到新的维度数。
4. matlab代码
function [tg xs q px newdt]=pca(h)
%数据标准化
h=zscore(h);
%计算相关系数矩阵
r=corrcoef(h);
disp('计算的相关系数矩阵如下:');
disp(r)
%计算特征向量与特征值
[x,y,z]=pcacov(r);
s=zeros(size(z));%创建0矩阵
for i=1:length(z)
s(i)=sum(z(1:i));
end
%主成分贡献率计算
disp('前几个特征根及其贡献率:');
disp([z,s])
tg=[z,s];
f=repmat(sign(sum(x)),size(x,1),1);
x=x.*f;
%主成分选择
n=input('请选择前n个需要计算的主成分:\n');
disp('由此可得选择的主成分系数分别为:');
for i=1:n
xs(i,:)=(x(:,i)');
end
newdt=h*xs';
disp('以主成分的贡献率为权重,构建主成分综合评价模型系数:');
q=((z(1:n)./100)')
w=input('是否需要进行主成分综合评价?(y or n)\n');
if w==y
df=h*x(:,1:n);
tf=df*z(1:n)/100;
[stf,ind]=sort(tf,'descend'); %按照降序排列
disp('主成分综合评价结果排序:');
px=[ind,stf]
else
return;
end