前言

随着分布式电源(distributed generation，DG)的渗透率不断提高，传统的配电网系统从被动单向的供电网络转变为功率双向流动的有源网络，使得配电网运行和控制面临诸多新挑战。依靠网络升级或运行结构变化等方法维持配电网可靠运行的成本高而且被动，将不再适用。采用主动策略来控制和管理配电网中的分布式可控资源成为系统运行方式优化以及提高可再生能源渗透率的主要手段。2008 年，国际大电网会议(CIGRE)提出了“配电网主动运行与发展”研究主题，主动配电网(active distribution network，ADN)是在主网和配网协同控制的基础上，具有分布式发电、储能和需求侧响应等电源、负荷调控手段，能够针对电力系统的实际运行状态，以安全性、经济性为调控目标，自适应调节其电源、网络及负荷的配电网。

基于支路潮流的无功优化控制模型

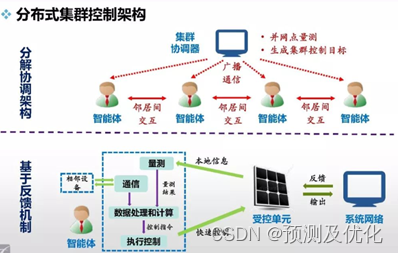
通常情况下ADN的电压和无功控制方法可分为2大类：集中式和分布式。集中式电压控制以系统全局为优化目标，统一调配可控资源，控制效果好，但控制策略的形成依赖于全网数据的监测和通信，一旦中央控制器故障，控制系统便会崩溃。分布式电压控制通常将系统分成若干个子区域，通过各子区域的控制和各子区域之间的协调，实现对整个网络的电压控制，摆脱了对中央控制器的依赖，减少了数据的量测与通信，提高了运行可靠性。

针对ADN中DG渗透率不断提高的特点，通过控制DG发出的无功以实现对ADN的电压优化控制。在ADN中，DG单元可分为可控性发电和不可控型发电。可控型发电包括小火电机组、燃气轮机和燃料电池等，不可控发电主要是风力和光伏等可再生能源发电，为了保证可再生能源最大化利用，一般要求风力和光伏电源采用最大功率点跟踪控制模式，有功功率固定在最大功率运行点，不参与协同控制。本程序控制可控型发电单元。

目标函数

对ADN的电压无功优化控制，除了要求系统中各节点电压控制在安全运行允许范围内，还要考虑系统运行的经济性，以系统运行的网络有功损耗作为目标函数：

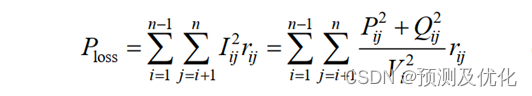
式中：Iij为线路ij传输电流；rij为线路ij电阻；Vi为节点i的电压；Pij、Qij为线路ij首端的传输功率。

约束条件

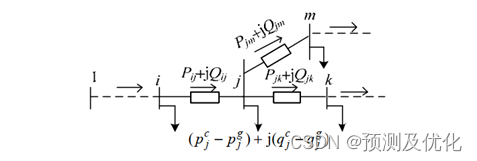
约束条件包含等式约束和不等式约束。等式约束为网络约束，不等式约束主要为控制变量上下限约束，状态变量上下限约束。其中网络约束采用支路潮流方程进行描述，如下图所示。

无功优化控制模型的凸化

上述AND无功优化控制模型中，等式约束DistFlow潮流方程包含复杂的二次项，使得优化问题非凸。分布式优化算法求解非凸的问题难以找到全局最优解，不能保证收敛性。为了分布式求解非凸的非线性规划问题，一般把非凸优化问题转变成为凸优化问题。无功优化问题凸化的方法有多种，常通过半定规划SDP、二阶锥规划SOCP对问题进行凸化。程序采用对DistFlow潮流方程进行合理简化的方法对原优化问题进行凸化。

简化的假设为：1）线路上的功率损耗远远小于线路本身传输的功率；2）节点之间的电压偏差远远小于节点电压本身。

基于分区的分布式无功优化控制模型

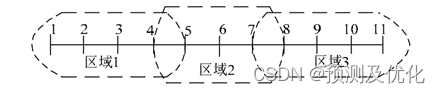
对于一个主动配电网系统，可用图G=(N,E)表示，其中N是全系统节点的集合，E是全系统支路的集合，eij∈E表示系统中某一支路，其中{i,j}∈N。对于优化问题可以按照物理区域分解为多个子系统的优化问题。如把配电网系统分成r个有联系的物理区域，以集合R表示；对于某个区域a，以Na表示区域a的节点集合，Ea表示区域a的支路集合，eij∈Ea表示区域a中某一支路。相邻区域之间的联系，通过区域边界上的支路进行耦合，即相邻区域共享某一支路。以下图所示配电系统为例，区域 的节点集合为{1,2,3,4,5}，区域2的节点集合为{4,5,6,7,8}，区域3的节点集合为{7,8,9,10,11}，区域1和区域2通过支路e45进行耦合，区域2和区域3通过支路e78进行耦合。耦合支路的集合用O:={eij|Ea∩Eb,Ɐa,b∈R且b≠a}表示。对于图示系统，耦合支路的集合O:={e45,e78}。耦合支路eij的状态变量包括支路传输的功率Pij、Qij，支路两端节点的电压平方Ui、Uj。区域a中耦合支路的状态以向量Xa,ij: {Pa,ij, Qa,ij,Ua,i,Ua,j}表示。

同步型ADMM分布式求解

基于分区协调的分布式无功优化控制模型是目标函数可分、边界耦合约束线性的凸规划模型，可采用同步型ADMM实现分布式求解。下面以原问题分解成为a，b2个区域协调的子问题为例，简述同步型ADMM分布式求解的过程。

程序介绍

程序基于分区协调控制和凸优化的思想，提出了一种主动配电网分布式无功优化控制方法。此方法以网络有功损耗为目标函数，考虑配电网潮流方程约束、各节点电压上下限约束和分布式电源无功出力上下限约束。以简化的支路潮流方程将非凸的无功优化控制问题转化成凸二次规划问题，以物理分区的形式对凸二次规划问题进行分布式计算求解。每个控制区域都配有一个独立的控制器，每个控制器仅对所控制区域数据进行测量，并且只收集相邻控制器的边界协调信息，采用同步型交替方向乘子法进行分布式优化计算，得到各区域分布式电源的无功优化控制策略。程序中算例丰富，注释清晰，干货满满，创新性和可扩展性很高，足以撑起一篇高水平论文！下面对程序做简要介绍！

程序适用平台：Matlab+Yalmip+Cplex

参考文献：《主动配电网分布式无功优化控制方法》-电网技术；

Tips：仅参考了文中IEEE33节点算例！

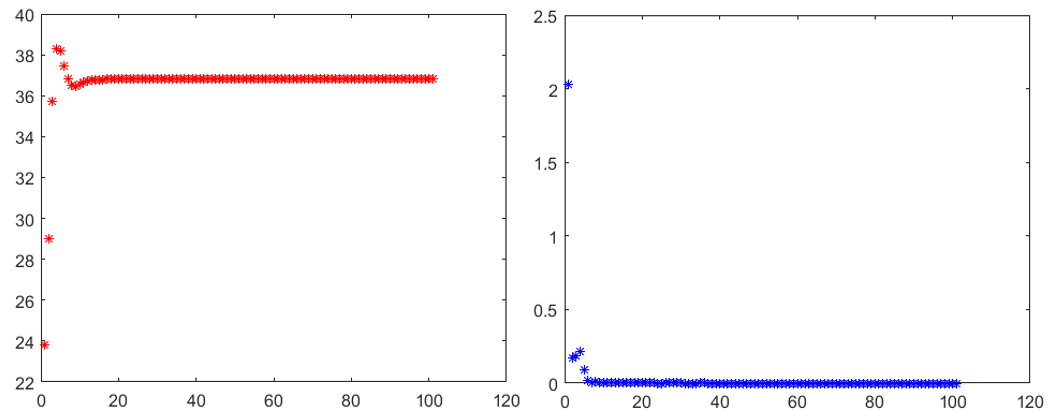
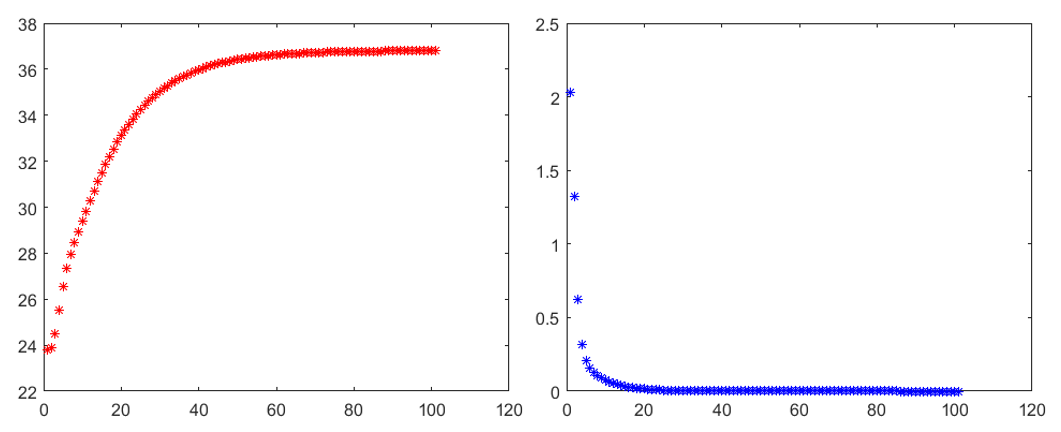
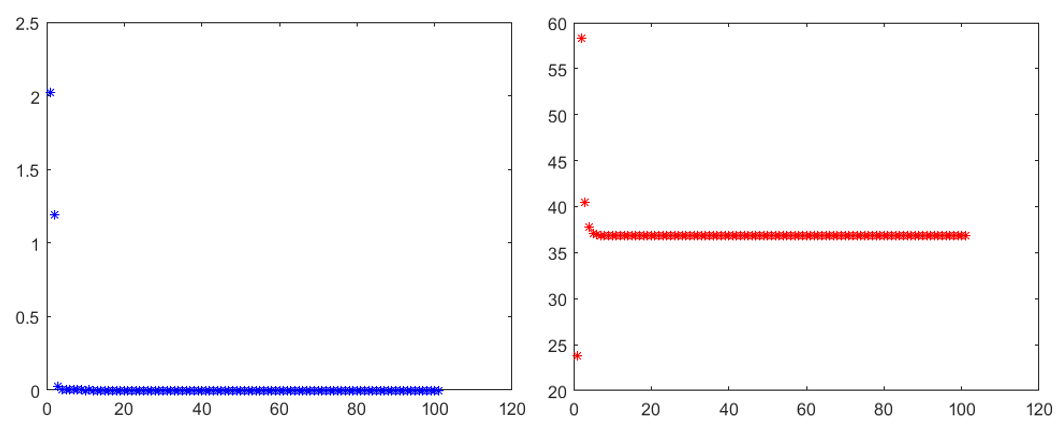
程序结果

部分程序

%%ADMM主程序%%串行计算​
%%%区域a,节点33,1-7,18-25
%%耦合为Xa=[U(6),U(7),P(7),Q(7),U(5),U(25),P(25),Q(25)]​
%%%区域b,节点6-17
%%耦合为Xb=[U(6),U(7),P(7),Q(7)]​
%%%区域c,节点5,25-32
%%耦合为Xb=[U(5),U(25),P(25),Q(25)]​
%%%%首轮求解
Ploss_data=zeros(32,1);​Volta_data=zeros(33,1);
Qg_data=zeros(33,1);xigma=0;lagrant_a=[0;0;0;0;0;0;0;0];lagrant_b=[0;0;0;0];lagrant_c=[0;0;0;0];​
lagrant_a=lagrant_a+xigma*(Xa-Xa_last);lagrant_b=lagrant_a(1:4);lagrant_c=lagrant_a(5:8);
figure(1)
%目标函数​%%%%迭代
for k=1:100
​[Xa,Ploss,Volta,Qg]=program_a(lagrant_a,xigma,Xa_last);
​Ploss_data(Line_a)=Ploss(Line_a);Volta_data(Node_a)=Volta(Node_a);Qg_data(Node_a)=Qg(Node_a);
Xb_last=Xa(1:4);​[Xb,Ploss,Volta,Qg]=program_b(lagrant_b,xigma,Xb_last);
​Ploss_data(Line_b)=Ploss(Line_b);Volta_data(Node_b)=Volta(Node_b);Qg_data(Node_b)=Qg(Node_b);
Xc_last=Xa(5:8);[Xc,Ploss,Volta,Qg]=program_c(lagrant_c,xigma,Xc_last);

部分内容源自网络，侵权联系删除！

欢迎感兴趣的小伙伴关注并私信获取完整版代码，小编会不定期更新高质量的学习资料、文章和程序代码，为您的科研加油助力！