解耦信息瓶颈
摘要: 信息瓶颈方法是一种从源随机变量中提取与预测目标随机变量相关的信息的技术,通常通过优化平衡压缩和预测项的IB拉格朗日乘子f来实现,然而拉格朗日乘子很难优化,需要多次实验来调整拉格朗日乘子的值,此外我们还证明了随着压缩强度的增大 预测性会严重降低,本文从监督解纠缠的角度来实现信信息瓶颈的方法,DisenIB 旨在保证目标与测性能不损失的前提下,最大化的压缩性信息源大量的理论和实验证明,我们的方法在最大压缩方面是一致性的,并且在泛化性能 对抗性攻击的鲁棒性 、分布外检测和监督解耦方面表现出色。
最大压缩方面是一致性的:最大化压缩源数据的同时,保持了目标预测性能的一致性,即在不损失预测性能的前提下实现最大压缩。
问题提出: 什么是信息瓶颈? 信息瓶颈的意义是什么?
信息瓶颈技术是一种基于信息论原理的方法,旨在从源随机变量中提取与目标随机变量预测相关的最小信息集合。它通过优化信息瓶颈的拉格朗日量(IB Lagrangian)来实现,这个拉格朗日量在压缩和预测项之间取得了平衡。简而言之,信息瓶颈技术试图在减少信息量的同时,保持或提高预测的准确性。
信息瓶颈提取出的信息 是从源随机变量中提取的,提取的约束是保持或者提高预测的准确性的前提下,减少信息量,即 用少量的信息实现最好的预测。
意义与应用:数据压缩(找到最优的中间表示)、特征选择(选择最具代表性的特征子集),和模型压缩(减少模型的复杂性和参数量)
1 introduction
压缩是机器学习中 普遍存在的任务,为了提高计算效率过度参数化的网络使用剪枝进行压缩,机器可以讲复杂的数据转化为可以泛化的压缩表示,确定数据的哪些方面可以保留,哪些方面可以舍弃是很重要的,信息瓶颈理论提供了一种原则性的方法来解决这个问题,它压缩源随机变量以保留与预测目标随机变量相关的信息,最近的研究表明,信息瓶颈的方法可以产生具有很好泛化性能的表征,并且有望解释神经网络的学习行为,给定随机变量X,Y 他们的联合概率分布是
T)信息瓶颈的方法旨在压缩信息X到一个瓶颈随机变量T 并且保持与预测随机变量的信息,也就是说寻找一个概率映射q(T|X) 使得互信息I(X;T)受限的同时最大化I(T;Y),这可以表述为一个约束优化问题
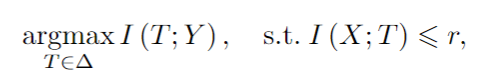
可以通过最小化拉格朗日量来解决这个问题:

最小化拉格朗日乘子遇到了很多问题 。。。。
我i们期望从X中提取出Y的最小充分表示,T,最大化压缩X 而不丢失互信息I(T;Y) 在本文其余部分称为最大压缩, 这种i情况不能通过最小化拉格朗日乘子来实现,因为压缩总要 减少 互信息I(T;Y) 此外 我们期待消除对多次优化的需要,并且探索 通过单个优化实现最大压缩一致的方法,我们一开始意识到监督解纠缠和信息瓶颈背后的思想密切相关,监督解纠缠解决的问题是 识别 互补的数据方面,并且通过监督学习的方式将他们解开,在信息瓶颈的方法中的 必须分离与Y相关和不相关的数据方面,这启发我们从监督解耦的角度来实现信息瓶颈的方法,据我们所知我们是第一个在信息瓶颈和解耦学习方面建立联系的研究,我们的贡献有下面三个方面:
•我们研究了IB拉格朗日量中的权衡,表明平衡压缩和预测项只会降低预测性能,因此无法实现最大压缩。
•我们提出了IB的一个变体,即解纠缠信息瓶颈(DisenIB),它被证明在最大压缩上是一致的。具体来说,DisenIB消除了多次优化的需要,并通过单个优化一致性执行最大压缩。
•通过实验结果,我们证明了我们的理论陈述,并表明DisenIB在概括(Shamir, Sabato, and Tishby 2010)、对抗性攻击的鲁棒性(Alemi et al. 2017)和分布外数据检测(Alemi, Fischer, and Dillon 2018)以及监督解缠方面表现良好
2 方法
在本节中,我们首先研究了IB拉格朗日量中涉及的权衡,表明平衡压缩和预测项只会降低预测性能,因此无法实现最大压缩。然后,我们介绍了我们提出的最大压缩一致的DisenIB。
2.1 IB拉格朗日权衡
我们首先证明了优化IB拉格朗日会导致不可避免的权衡。具体来说,通过优化IB拉格朗日量得到的压缩目标和预测目标的最优解始终不如单独优化每个目标得到的最优解。这可以用定理1(见补充证明)来正式表述:

2.2一致性
由于上述权衡,优化IB拉格朗日量无法实现最大压缩。期望探索一种能够执行最大压缩的方法。此外,我们还希望消除对多重优化的需求。也就是说,我们期望探索一种通过单个优化始终如一地执行最大压缩的方法,这被称为最大压缩的一致性属性。。。。。。
2.3 Disentangled IB
我们介绍了我们的方法在最大压缩方面是一致的,在认识到信息瓶颈和解耦之间的关系后,我们从监督解耦分类角度实现信息瓶颈,我们引入另一个变量S 作为 与T 互补的方面表示 T 表示的是从X中提取出的能够预测Y的最小信息量 S 可以简单理解为 冗余无关信息。
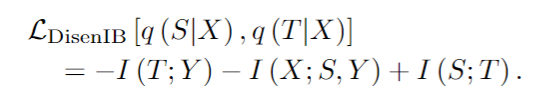
具体来说,我们鼓励(S, Y)通过最大化I (X;S, Y),使得S至少涵盖了与Y无关的数据方面的信息。我们鼓励Y可以通过最大化I (T;Y),使得T至少涵盖了Y相关数据方面的信息。因此,存储在S和T中的信息量都是下界的。在这种情况下,通过最小化I (S;T)消除了它们之间的重叠信息,从而收紧了两个边界,使确切的信息保持相关。此外,通过优化LDisenIB可以一致地实现最大压缩,如下定理2所示(见补充证明):
定理2 LDisenIB在最大压缩上是一致的。
我们推导出I (T;Y)的变分近似;Y)和I (X;S, Y)项 通过引入变分概率映射p (y|t)和R (x|s, y),可处理的变分下界可表示为

最小化I (S;T) = DKL [q (S, T)‖q (S) q (T)]项是难以处理的,因为q (S, T)和q (S) q (T)都涉及具有大量组分的混合物。然而,我们观察到,由于马尔可夫链s↔x↔t (Kim and Mnih 2018),我们可以有效地从联合分布q (s, t)中抽样,首先从数据集中均匀随机抽样x,然后从q (s, t|x) = q (s|x) q (t|x)抽样。我们还可以通过沿着批轴对联合分布q (s, t)中的样本进行洗牌,从边际分布q (s) q (t)的乘积中进行抽样(Belghazi et al. 2018)。然后,我们使用密度比率技巧通过引入一个判别器d来估计其输入是来自q (s, t)而不是来自q (s) q (t)的样本的概率。对抗训练是用来训练鉴别器的
当达到纳什均衡Nash equilibrium时,q (s, t) = q (s) q (t),从而使它们的互信息I (S; T )项最小