Rocky Ding

公众号：WeThinkIn

写在前面

【三年面试五年模拟】栏目专注于分享AI行业中实习/校招/社招维度的必备面积知识点与面试方法，并向着更实战，更真实，更从容的方向不断优化迭代。也欢迎大家提出宝贵的意见或优化ideas，一起交流学习💪

大家好，我是Rocky。

本文是“三年面试五年模拟”之独孤九剑秘籍的第十二式，之前我们将独孤九剑秘籍前六式进行汇总梳理成汇总篇，并制作成pdf版本，大家可在公众号后台 【精华干货】菜单或者回复关键词“三年面试五年模拟” 进行取用。

除此之外Rocky还将YOLOv1-v7全系列大解析也制作成相应的pdf版本，大家可在公众号后台 【精华干货】菜单或者回复关键词“YOLO” 进行取用。

由于【三年面试五年模拟】系列都是Rocky在工作之余进行整理总结，难免有疏漏与错误之处，欢迎大家对可优化的部分进行指正，我将在后续的优化迭代版本中及时更正。

在【人人都是算法工程师】算法工程师的“三年面试五年模拟”之独孤九剑秘籍（先行版）中我们阐述了这个program的愿景与规划。本系列接下来的每一篇文章都将以独孤九剑秘籍框架的逻辑展开，考虑到易读性与文章篇幅，一篇文章中只选取每个分支技能树中的2-3个经典&高价值知识点和面试问题，并配以相应的参考答案（精简版），供大家参考。

希望独孤九剑秘籍的每一式都能让江湖中的英雄豪杰获益。

So，enjoy（与本文的BGM一起食用更佳哦）：

干货篇

----【目录先行】----

深度学习基础：

什么是转置卷积的棋盘效应？
Instance Normalization的作用？

经典模型&&热门模型：

Focal Loss的作用？
YOLO系列的面试问题

机器学习基础：

机器学习有哪些种类？
L1正则为什么比L2正则更容易产生稀疏解?

Python/C/C++知识：

Python中assert的作用？
Python中互换变量有不用创建临时变量的方法吗？
C/C++中野指针的概念？

模型部署：

什么是异构计算？
端侧部署时整个解决方案的核心指标？

图像处理基础：

有哪些常用的图像质量评价指标？
什么是图像畸变？

开放性问题：

不同性质的公司如何使用好AI技术？
新时期的AI Lab该如何搭建？

----【深度学习基础】----

【一】什么是转置卷积的棋盘效应？

造成棋盘效应的原因是转置卷积的不均匀重叠（uneven overlap）。这种重叠会造成图像中某个部位的颜色比其他部位更深。

在下图展示了棋盘效应的形成过程，深色部分代表了不均匀重叠：

棋盘效应

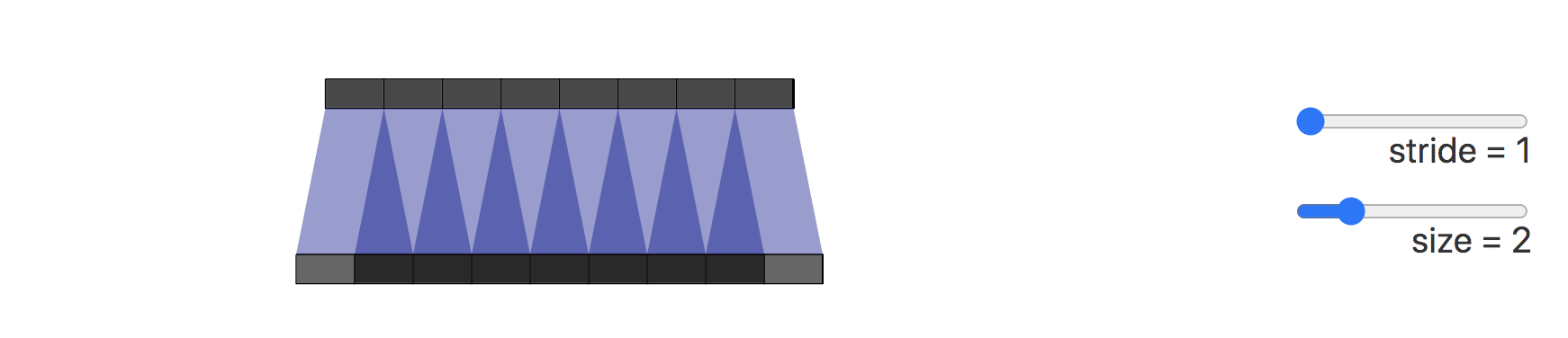
接下来我们将卷积步长改为2，可以看到输出图像上的所有像素从输入图像中接收到同样多的信息，它们都从输入图像中接收到一个像素的信息，这样就不存在转置卷带来的重叠区域。

我们也可以直接进行插值Resize操作，然后再进行卷积操作来消除棋盘效应。这种方式在超分辨率重建场景中比较常见。例如使用双线性插值和近邻插值等方法来进行上采样。

【二】Instance Normalization的作用？

Instance Normalization（IN）和Batch Normalization（BN）一样，也是Normalization的一种方法，只是IN是作用于单张图片，而BN作用于一个Batch。

BN对Batch中的每一张图片的同一个通道一起进行Normalization操作，而IN是指单张图片的单个通道单独进行Normalization操作。如下图所示，其中C代表通道数，N代表图片数量（Batch）。

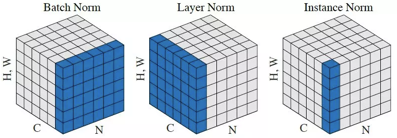
IN适用于生成模型中，比如图片风格迁移。因为图片生成的结果主要依赖于某个图像实例，所以对整个Batch进行Normalization操作并不适合图像风格化的任务，在风格迁移中使用IN不仅可以加速模型收敛，并且可以保持每个图像实例之间的独立性。

下面是IN的公式：

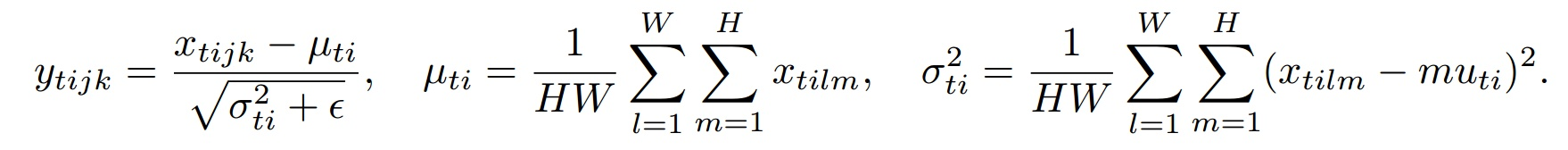
其中t代表图片的index，i代表的是feature map的index。

----【经典模型&&热门模型】----

【一】Focal Loss的作用？

Focal Loss是解决了分类问题中类别不均衡、分类难度差异的一个损失函数，使得模型在训练过程中更加聚焦在困难样本上。

Focal Loss是从二分类问题出发，同样的思想可以迁移到多分类问题上。

我们知道二分类问题的标准loss是交叉熵：

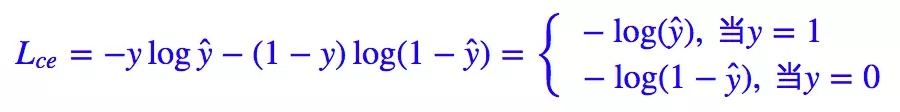
在这里插入图片描述
对于二分类问题我们也几乎适用sigmoid激活函数 $\hat{y} = \sigma(x)$ ，所以上面的式子可以转化成：

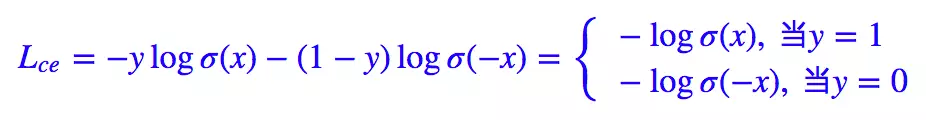
在这里插入图片描述
这里有 $\sigma(x) = \sigma(-x)$ 。

Focal Loss论文中给出的式子如下：

其中 $y\in \{ 1,-1\}$ 是真实标签， $p\in[0,1]$ 是预测概率。

我们再定义 $p_{t}:$

那么，上面的交叉熵的式子可以转换成：

有了上面的铺垫，最初Focal Loss论文中接着引入了均衡交叉熵函数：

针对类别不均衡问题，在Loss里加入一个控制权重，对于属于少数类别的样本，增大 $\alpha_{t}$ 即可。但这样有一个问题，它仅仅解决了正负样本之间的平衡问题，并没有区分易分/难分样本。

为什么上述公式只解决正负样本不均衡问题呢？

因为增加了一个系数 $\alpha_{t}$ ，跟 $p_{t}$ 的定义类似，当 $l ab e l = 1$ 的时候 $\alpha_{t}=\alpha$ ;当 $l ab e l = - 1$ 的时候， $\alpha_{t}= 1 - \alpha$ ， $\alpha$ 的范围也是 $[0, 1]$ 。因此可以通过设定 $\alpha$ 的值（如果 $1$ 这个类别的样本数比 $- 1$ 这个类别的样本数少很多，那么 $\alpha$ 可以取 $0.5$ 到 $1$ 来增加 $1$ 这个类的样本的权重）来控制正负样本对整体Loss的贡献。

Focal Loss

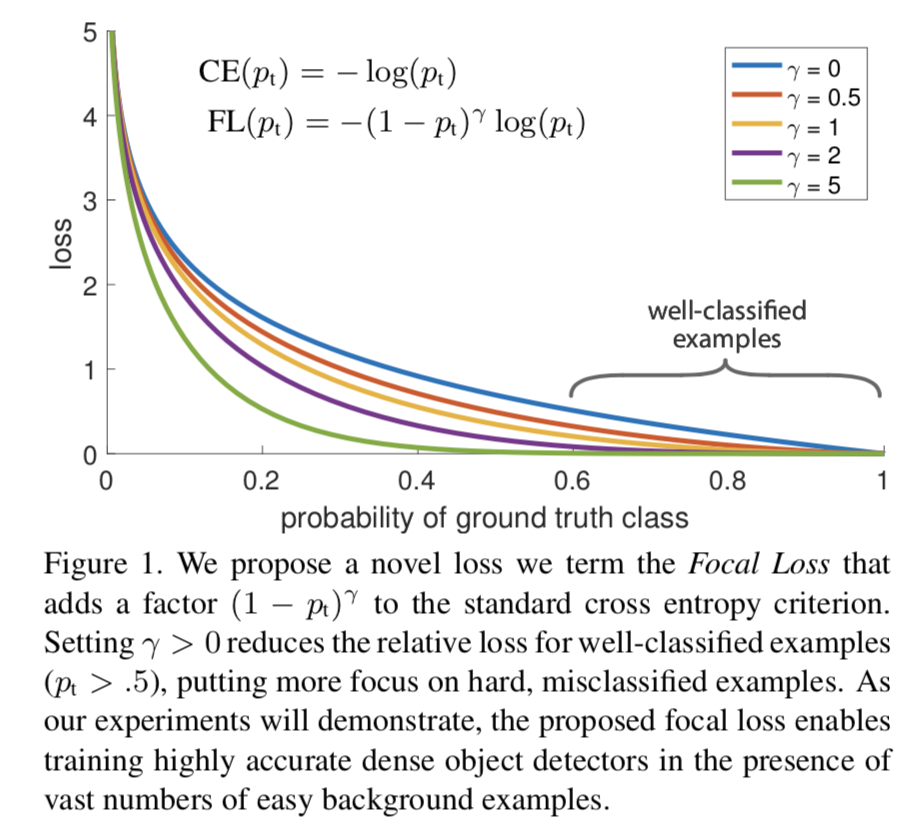
为了可以区分难/易样本，Focal Loss雏形就出现了：

$p_{t})^{\gamma}$ 用于平衡难易样本的比例不均， $\gamma >0$ 起到了对 $1 - p_{t})$ 的放大作用。 $\gamma >0$ 减少易分样本的损失，使模型更关注于困难易错分的样本。例如当 $\gamma =2$ 时，模型对于某正样本预测置信度 $p_{t}$ 为 $0.9$ ，这时 $0.9)^{\gamma} = 0.01$ ，也就是FL值变得很小；而当模型对于某正样本预测置信度 $p_{t}$ 为0.3时， $0.3)^{\gamma} = 0.49$ ，此时它对Loss的贡献就变大了。当 $\gamma = 0$ 时变成交叉熵损失。

为了应对正负样本不均衡的问题，在上面的式子中再加入平衡交叉熵的 $\alpha_{t}$ 因子，用来平衡正负样本的比例不均，最终得到Focal Loss：

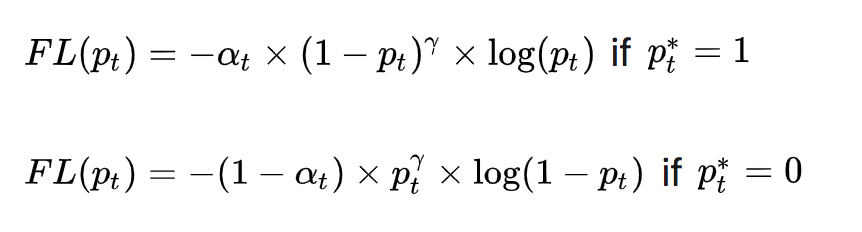
Focal Loss论文中给出的实验最佳取值为 $a_{t}= 0.25$ ， $\gamma = 2$ 。

【二】YOLO系列的面试问题

Rocky之前总结了YOLOv1-v7全系列的解析文章，帮助大家应对可能出现的与YOLO相关的面试问题，大家可按需取用：

【Make YOLO Great Again】YOLOv1-v7全系列大解析（汇总篇）

----【机器学习基础】----

【一】机器学习有哪些种类？

机器学习中通常根据数据是否有标签可以分为监督学习(supervised learning)、非监督学习(unsupervised learning)，半监督学习(semi-supervised learning)以及弱监督学习(weakly supervised learning)。

监督学习

机器学习模型在训练过程中的所有数据都有标签，就是监督学习的逻辑。

监督学习是最常见的学习种类，常见场景为分类和回归问题。

深度学习模型大都数都遵从监督学习的流程，并且支持向量机(Support Vector Machine, SVM)，朴素贝叶斯(Naive Bayes)，逻辑回归(Logistic Regression)，K近邻(K-Nearest Neighborhood, KNN)，决策树(Decision Tree)，随机森林(Random Forest)，AdaBoost以及线性判别分析(Linear Discriminant Analysis, LDA)等也属于监督学习算法的范畴。

非监督学习

非监督学习与监督学习完全相反，机器学习模型在训练过程中的所有数据都是没有标签的，主要学习数据本身的一些特性。

比如想象一个人从来没有见过猫和狗，如果给他看了大量的猫和狗，虽然他还是没有猫和狗的概念，但是他是能够观察出每个物种的共性和两个物种间的区别的，并对这个两种动物予以区分。

半监督学习

半监督学习的逻辑是机器学习模型在训练过程中，部分数据有标签，与此同时另外一部分数据没有标签，并把这两种数据都利用起来用于训练。

弱监督学习

弱监督学习的逻辑是机器学习模型在训练过程中使用的数据的标签存在不可靠的情况。这里的不可靠可以是标注不正确，多重标记，标记不充分，局部标记，包含噪声等情况。一个直观的例子是相对于分割的标签来说，分类的标签就是弱标签。

【二】L1正则为什么比L2正则更容易产生稀疏解?

我们首先可以设目标函数为 $L$ ，目标函数中的权值参数为 $w$ ，那么目标函数和权值参数的关系如下所示：

如上图所示，最优的 $w$ 在绿色的点处，而且 $w$ 非零。

我们首先可以使用L2正则进行优化，新的目标函数： $L + CW^{2}$ ，示意图如下蓝线所示：

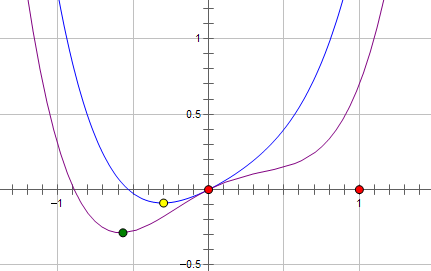
我们可以看到，最优的 $w$ 出现在黄点处， $w$ 的绝对值减小了，更靠近横坐标轴，但是依然是非零的。

为什么是非零的呢？

我们可以对L2正则下的目标函数求导：

我们发现，权重 $w$ 每次乘上的是小于1的倍数进行收敛，而且其导数在 $w = 0$ 时没有办法做到左右两边导数异号，所以L2正则使得整个训练过程稳定平滑，但是没有产生稀疏性。

接下来我们使用L1正则，新的目标函数： $L + C ∣ w ∣$ ，示意图如下粉线所示：

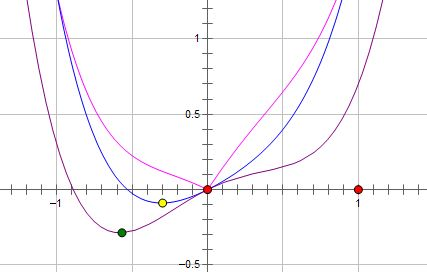
这里最优的 $w$ 就变成了0。因为保证使用L1正则后 $x = 0$ 处左右两个导数异号，就能满足极小值点形成的条件。

我们来看看这次目标函数求导的式子：

可以看出L1正则的惩罚很大， $w$ 每次都是减去一个常数的线性收敛，所以L1比L2更容易收敛到比较小的值，而如果 $C > |f^{'}(0)|$ ，就能保证 $w = 0$ 处取得极小值。

上面只是一个权值参数 $w$ 。在深层网路中，L1会使得大量的 $w$ 最优值变成0，从而使得整个模型有了稀疏性。

----【Python/C/C++知识】----

【一】Python中assert的作用？

Python中assert（断言）用于判断一个表达式，在表达式条件为 $f a l se$ 的时候触发异常。

断言可以在条件不满足程序运行的情况下直接返回错误，而不必等待程序运行后出现崩溃的情况。

Rocky直接举一些例子：

>>> assert True 
>>> assert False
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
AssertionError
>>> assert 1 == 1
>>> assert 1 == 2
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
AssertionError
>>> assert 1 != 2

【二】Python中互换变量有不用创建临时变量的方法吗？

在Python中，当我们想要互换两个变量的值或将列表中的两个值交换时，我们可以使用如下的格式进行，不需要创建临时变量：

x, y = y, x

这么做的原理是什么呢？

首先一般情况下Python是从左到右解析一个语句的，但在赋值操作的时候，因为是右值具有更高的计算优先级，所以需要从右向左解析。

对于上面的代码，它的执行顺序如下：

先计算右值 $y, x$ (这里是简单的原值，但可能会有表达式或者函数调用的计算过程)，在内存中创建元组(tuple)，存储 $y, x$ 分别对应的值；计算左边的标识符，元组被分别分配给左值，通过解包(unpacking)，元组中第一个标示符对应的值 $(y)$ ，分配给左边第一个标示符 $(x)$ ，元组中第二个标示符对应的值 $(x)$ ，分配给左边第二个标示符 $(y)$ ，完成了 $x$ 和 $y$ 的值交换。