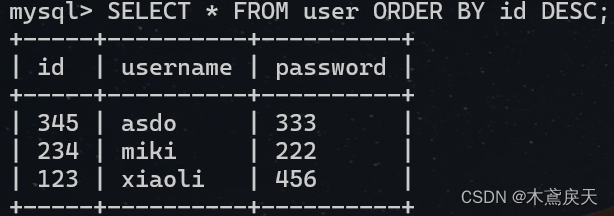
鲁棒控制（Robust Control）是一种控制系统设计方法，其目标是使控制系统在面临参数摄动、外部干扰、建模误差等不确定性因素时，仍能够保持其期望的性能特性。鲁棒性是指控制系统在一定（结构，大小）的参数摄动下，维持某些性能的特性。

根据对性能的不同定义，鲁棒性可分为稳定鲁棒性和性能鲁棒性。稳定鲁棒性主要关注系统在面对不确定性时能否保持稳定，而性能鲁棒性则关注系统能否在不确定性影响下维持其性能指标。

鲁棒控制理论在工业自动化、航空航天、机械制造等领域有广泛应用。其主要的理论原理是在设计控制器时尽量利用不确定性信息，使控制器能够容忍不确定性参数的出现，并在一定范围内保持系统的稳定性和性能。

鲁棒控制的主要方法包括H∞控制理论、结构奇异值理论（μ理论）等。其中，H∞控制理论是一种基于频域特性的控制理论，它通过对系统频域特性的整形来实现对系统性能的优化。而结构奇异值理论则是一种基于系统结构特性的控制理论，它通过对系统结构特性的分析来设计控制器，使系统在面对不确定性时仍能保持其性能。

控制器综合结构

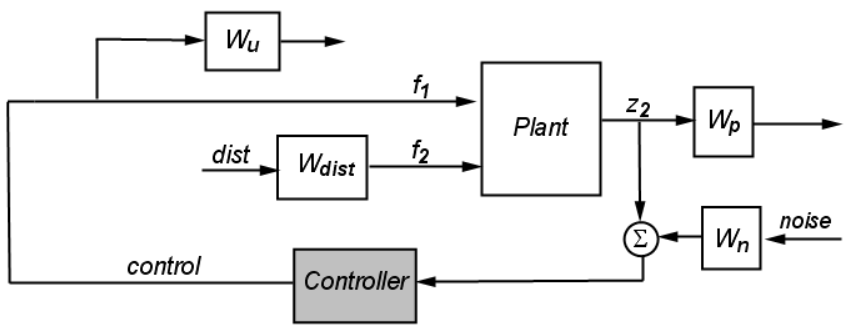
鲁棒控制器综合结构是一个设计过程，旨在构建能够在存在不确定性（如模型误差、外部干扰等）时维持系统性能和稳定性的控制器。这个过程涉及对控制系统的深入分析，并设计合适的控制策略来应对潜在的不确定性和扰动。

在鲁棒控制中，有几种关键的综合方法，如回路成形、H∞控制和结构奇异值（SSV）μ综合方法。其中，μ综合方法是一种多变量鲁棒控制设计方法，特别适用于设计满足多个性能要求的鲁棒控制器。在μ综合中，性能指标可以包括灵敏度、扰动响应、稳定裕度等多个方面，并通过确定权重函数或合成函数将这些指标加权或组合在一起。

在鲁棒控制器的综合结构中，通常会引入增广的对象模型，以表示系统的不确定性。这个模型可以包含系统的不确定性参数和可能的扰动。然后，通过选择合适的控制算法（如自适应控制、鲁棒控制、模糊控制等），并设计合适的控制器结构（如状态反馈控制器、输出反馈控制器等），来确保系统在面对不确定性时仍能保持其稳定性和性能。

鲁棒控制器的综合结构还需要考虑系统的硬件结构和传感器配置。高性能的传感器可以提供准确的系统状态信息，而合理的硬件结构可以确保控制器能够实时、准确地响应系统的变化。

鲁棒控制器综合结构是一个复杂的过程，需要综合考虑系统的不确定性、性能指标、硬件结构和传感器配置等多个方面。通过合理的设计和综合，可以构建出能够在存在不确定性时仍能保持高性能和稳定性的鲁棒控制器。

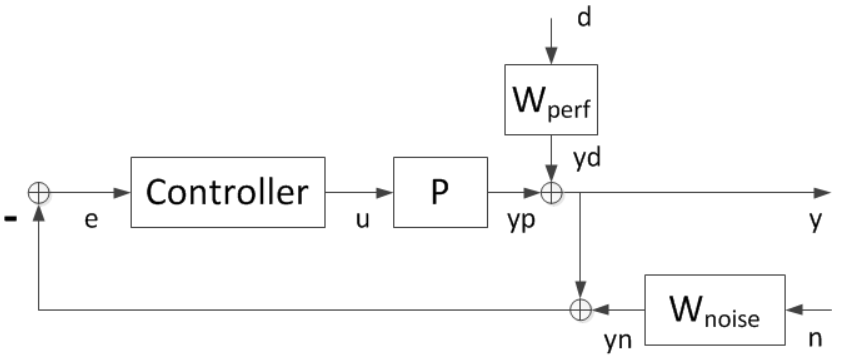
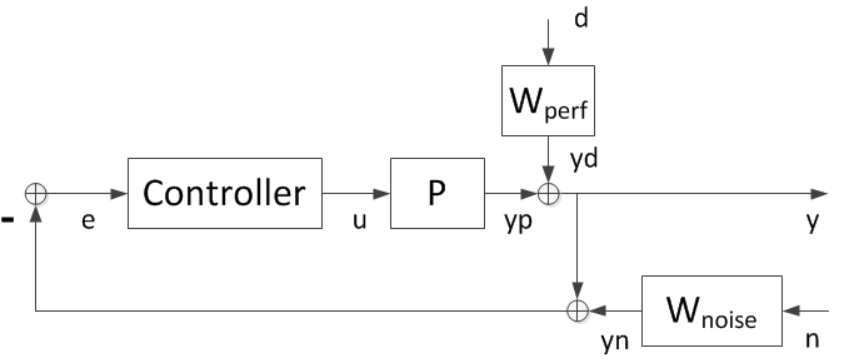
为了设计不确定对象P的鲁棒控制器，选择目标闭环带宽desBW，并使用简化的不确定性模型Usys进行灵敏度最小化设计。控制结构如下图所示。主要信号是干扰d、测量噪声n、控制信号u和被控对象输出y。滤波器Wperf和Wnoise反映了干扰和噪声信号的频率含量，或者等价地，反映了需要良好抗干扰和抗噪性能的频段。

我们的目标是通过抑制干扰d和最小化测量噪声n的影响来保持y接近于零。同样，我们想设计一个控制器，使增益从[d;n]到y“小”。请注意,

因此，感兴趣的传递函数由灵敏度函数1/(1+PC)和互补灵敏度函数PC/(1+PC)的性能加权和噪声加权组成。

D-K ITERATION SUMMARY:
-----------------------------------------------------------------
                       Robust performance               Fit order
-----------------------------------------------------------------
  Iter         K Step       Peak MU       D Fit             D
    1           223.6        100.4        101.4             2
    2           20.15        1.759        1.774            10
    3          0.9757       0.9681       0.9787            10
    4          0.9289       0.9289       0.9367             8
    5          0.9117       0.9118       0.9139            10
    6          0.9053       0.9053        0.906            10
    7           0.898        0.898        0.907            10
    8          0.8959       0.8959       0.8984            10
    9          0.8946       0.8946       0.8969             8

Best achieved robust performance: 0.895

鲁棒性能muBound是一个正标量。如果它接近于1，则说明设计成功，所需的有效闭环带宽匹配紧密。根据经验，如果muBound小于0.85，则可以提高可实现的性能。当muBound大于1.2时，对于给定的植物不确定性量，则无法实现所需的闭环带宽。

由于这里的muBound值大约为0.9，因此达到了目标，但最终还需要改进。为了验证目的，创建不同不确定度值的开环响应的波德图，并注意典型的零db交叉频率和相位裕度:

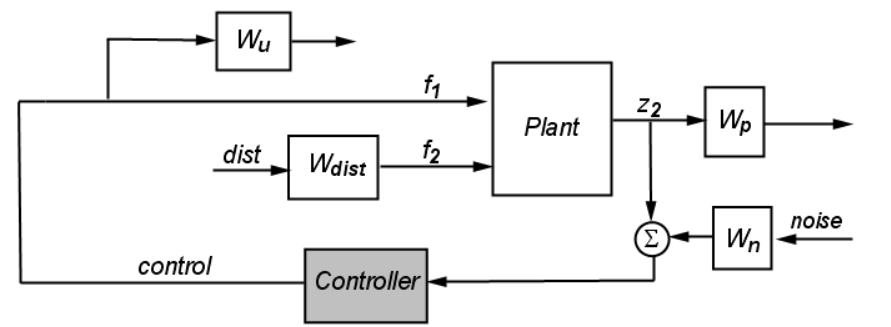
有重要的动力学和饱和与执行器相关，所以想要包括执行器模型。在使用的频率范围内，可以将执行器建模为具有速率和幅度饱和度的一阶系统。对于大多数信号，限制执行器性能的是速率限制，而不是极点位置。对于线性模型，速率限制的一些影响可以包含在扰动模型中。

控制结构

选择过滤器Wperf和Wnoise来实现所需的带宽和适当的滚降。从[d;n]到y的闭环传递函数为

y = [Wperf * S, Wnoise * T] [d;n]
其中S=1/(1+PC)、T=PC/(1+PC)分别为灵敏度函数和互补灵敏度函数。如果我们设计一个控制器，使闭环增益从[d;n]到y小于1，则

|S| < 1/|Wperf|， |T| < 1/|Wnoise|
通过为Wperf和Wnoise选择适当的幅度曲线，我们可以在带宽内实现较小的灵敏度(S)，并在带宽外实现足够的滚降(T)。