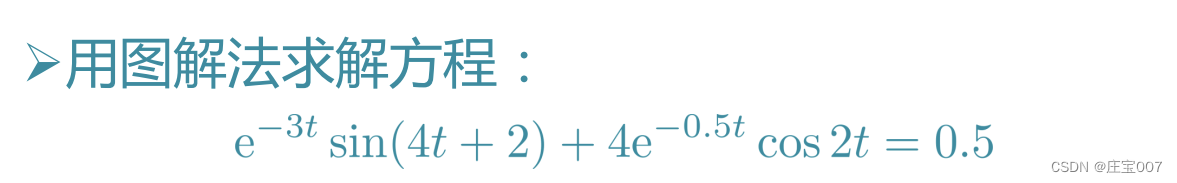
>> ezplot('exp(-3*t)*sin(4*t+2)+4*exp(-0.5*t)*cos(2*t)-0.5',[0 5]),
line([0 5],[0 0])

验证

>> t=0.6738;
>> exp(-3*t)*sin(4*t+2)+4*exp(-0.5*t)*cos(2*t)-0.5

ans =

  -2.9852e-04

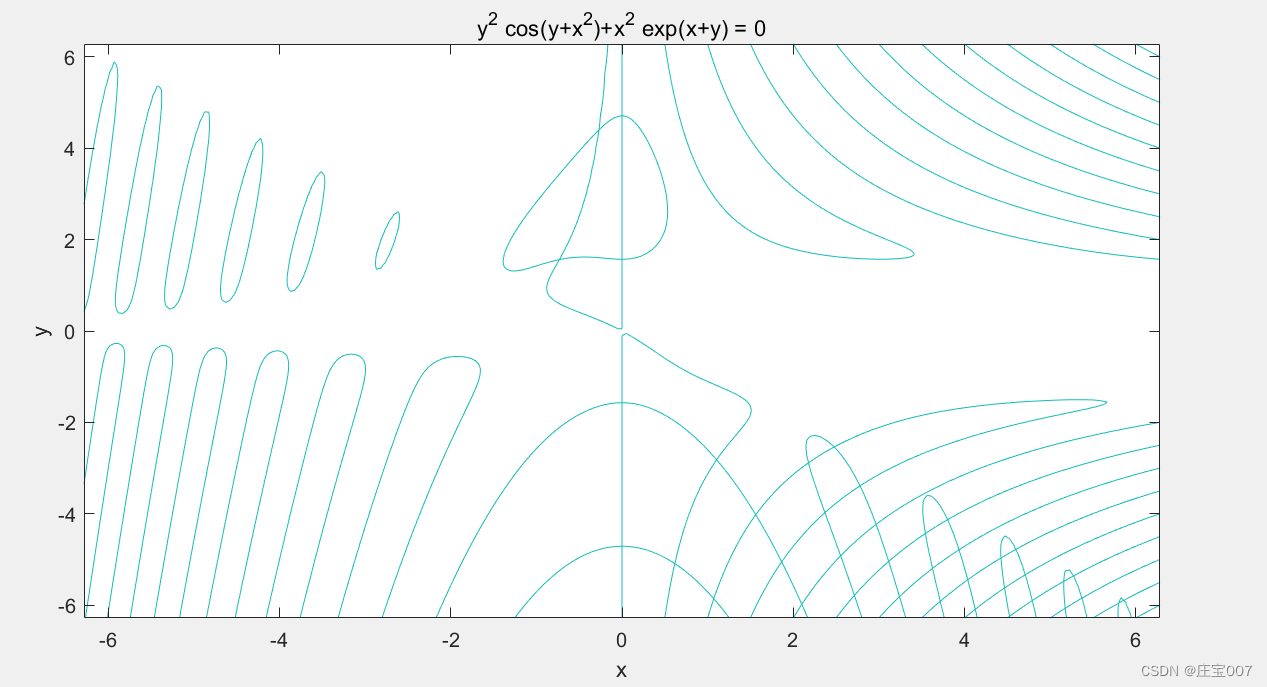
>> ezplot('x^2*exp(-x*y^2/2)+exp(-x/2)*sin(x*y)')
>> hold on; ezplot('y^2*cos(y+x^2)+x^2*exp(x+y)')

 

ezplot('x^2+y^2-1'); hold on, ezplot('0.75*x^3-y+0.9')

多项式型方程的准解析解方法

 准解析解的精度要远远高于双精度意义下的数值解

>>  syms x y; [x0 y0]=solve(x+y==35,2*x+4*y==94)
 
x0 =
 
23
 
 
y0 =
 
12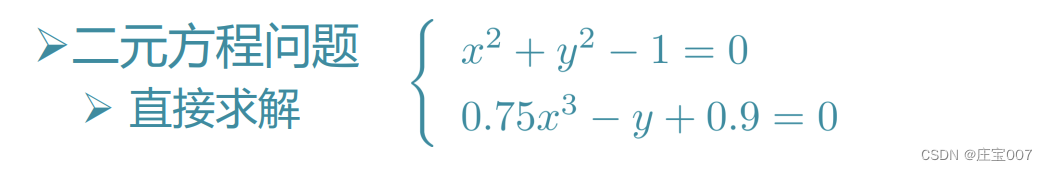

>>  [x1,y1]=vpasolve(x^2+y^2-1==0,75*x^3/100-y+9/10==0)
 
x1 =
 
    0.8663180988361181101678980941865 + 1.2153712664671427801318378544391i
    0.8663180988361181101678980941865 - 1.2153712664671427801318378544391i
- 0.55395176056834560077984413882735 - 0.35471976465080793456863789934944i
- 0.55395176056834560077984413882735 + 0.35471976465080793456863789934944i
                                        0.35696997189122287798839037801365
                                       -0.98170264842676789676449828873194
 
 
y1 =
 
- 1.4916064075658223174787216959257 + 0.7058820072140226775391882713884i
- 1.4916064075658223174787216959257 - 0.7058820072140226775391882713884i
 0.92933830226674362852985276677202 - 0.2114382218589592361562338176221i
 0.92933830226674362852985276677202 + 0.2114382218589592361562338176221i
                                      0.93411585960628007548796029415446
                                       0.1904203509918773024097775641529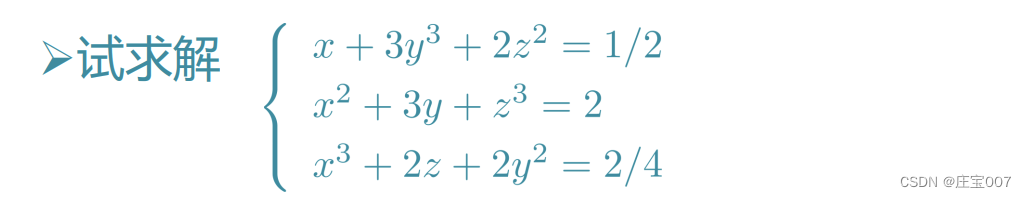

syms x y z; F=[x+3*y^3+2*z^2-1/2, x^2+3*y+z^3-2, x^3+2*z+2*y^2-2/4]; [x0,y0,z0]=vpasolve(F,[x,y,z]), size(x0)

使用了符号工具箱（Symbolic Toolbox）进行符号计算。1. `syms x y z;`: 这一行定义了符号变量 `x`、`y` 和 `z`，使它们成为符号对象，而不是普通的数值变量。这样定义的符号变量可以进行符号运算。2. `F=[......];`: 这一行定义了一个包含三个方程的方程组 `F`。每个方程都是关于 `x`、`y` 和 `z` 的符号表达式。方程组的目标是找到满足这三个方程的 `x`、`y` 和 `z` 的值。（向量型的方程解析表达式）3. `[x0,y0,z0]=vpasolve(F,[x,y,z]), size(x0)`: 这一行利用 `vpasolve` 函数求解方程组 `F`，并将解保存在变量 `x0`、`y0` 和 `z0` 中。`vpasolve` 是用于求解包含符号变量的方程组的函数。`[x0,y0,z0]` 将解分别赋给 `x0`、`y0` 和 `z0`。最后，`size(x0)` 返回解向量 `x0` 的大小，即解的个数。所以，这段代码的作用是解方程组 `F`，并返回解的个数。解向量 `x0`、`y0` 和 `z0` 包含了方程组的解。

>>  norm(subs(F,{x,y,z},{x0,y0,z0}))
 
ans =
 
6.1612263763129763734660360111682e-34

计算方程组 `F` 在求解后得到的 `x0`、`y0` 和 `z0` 值处的误差向量的二范数。1. `subs(F,{x,y,z},{x0,y0,z0})`: 这一部分使用 `subs` 函数，将方程组 `F` 中的符号变量 `x`、`y` 和 `z` 替换为它们的解 `x0`、`y0` 和 `z0`，生成了一个数值的向量。这个向量代表了在解 `x0`、`y0` 和 `z0` 处，方程组的每个方程的数值结果。2. `norm(...)`: 在这里用于计算误差向量的二范数，即向量的模。综合起来，`norm(subs(F,{x,y,z},{x0,y0,z0}))` 的作用就是计算方程组 `F` 在求解后得到的 `x0`、`y0` 和 `z0` 值处的误差向量的二范数，从而衡量求解结果的精确度。

 syms x y; F=[x^2/2+x+3/2+2/y+5/(2*y^2)+3/x^3; y/2+3/(2*x)+1/x^4+5*y^4]; [x0,y0]=vpasolve(F,[x,y]), size(x0) 

>> norm(subs(F,{x,y},{x0,y0}))
 
ans =
 
1.7815462397351061220372854390882e-33

>> syms a b x y; [x1,y1]=solve(x^2+a*x^2+6*b+3*y^2==0,y==a+(x+3),[x,y])
 
x1 =
 
(4*a + 3^(1/2)*(- 15*a - 8*b - 2*a*b - 7*a^2 - a^3 - 9)^(1/2) + a^2 + 3)/(a + 4) - a - 3
(4*a - 3^(1/2)*(- 15*a - 8*b - 2*a*b - 7*a^2 - a^3 - 9)^(1/2) + a^2 + 3)/(a + 4) - a - 3
 
 
y1 =
 
(4*a + 3^(1/2)*(- 15*a - 8*b - 2*a*b - 7*a^2 - a^3 - 9)^(1/2) + a^2 + 3)/(a + 4)
(4*a - 3^(1/2)*(- 15*a - 8*b - 2*a*b - 7*a^2 - a^3 - 9)^(1/2) + a^2 + 3)/(a + 4)