文章目录
- 前言
- 了解AVL树
- AVL树的特点
- AVL树的节点
- 调整方案
- 右单旋
- 为什么要右单旋呢?
- 右单旋代码
- 左单旋
- 为什么要左单旋?
- 左单旋代码
- 左右双旋
- 左右双旋之后平衡因子的情况
- 左右双旋代码实现
- 右左双旋
- 右左双旋代码:
- 简单测试
前言
回顾我们对于二叉搜索树的了解,二叉搜索树的效率跟树的高度成反比。而且,数据插入的随机性导致普通的二叉搜索树甚至可能退化成一条“单链表”,这样的结构查找起来时间复杂度直奔O(N),这无疑是我们不想看到的。我们希望,无论数据怎么插入,二叉搜索树的结构都应该保持平衡,即看起来更加接近于完全二叉树或者满二叉树·。AVL树因此诞生。
了解AVL树
AVL树又叫平衡二叉搜索树,得名于它的发明者Georgy Adelson-Velsky和Evgenii Landis。它的出现很好的解决了二叉搜索树的效率退化问题。AVL树的特点就是任一一个节点的左右子树的高度差不超过1。这个特点可以使二叉搜索树的高度始终保持在logn的级别,从而保证了查找效率稳定在O(logn)级别。具体是怎么实现这一特点的呢?下面结合代码给您讲解。
AVL树的特点
- AVL树具有二叉搜索树的性质,即对于任意一个节点,左子树的值均小于根节点的值,右子树的值均大于根节点的值。
- 每个节点都有一个平衡因子属性(可视为一个int变量),记录着左右子树的高度差(一般是右子树高度减去左子树高度)
- 查找、删除、插入的时间复杂度均为O(logn).
AVL树的节点
根据AVL树的特点,AVL树的每一个节点都得有一个记录左右子树高度差的平衡因子。除此之外,还需要有一个指向父节点的指针。具体如下:
//节点信息
template<class K, class V>
class AVLNode {
public:
AVLNode(const pair<K, V>& kv)
:_bf(0)
, left(nullptr)
, right(nullptr)
,father(nullptr)
{
}
int _bf;//平衡因子
pair<K, V> _kv;
AVLNode<K, V>* left;
AVLNode<K, V>* right;
AVLNode<K, V>* father;
};
调整方案
下面所述代码中,平衡二叉树的平衡因子均表示右子树高度减去左子树高度。
当我们向一颗平衡二叉树里插入一个元素,插入节点的祖先节点的平衡因子都有可能会因此改变。从当前新节点的父节点开始向上遍历,重复以下几个步骤:
- 用一个指针指
cur向新节点表示当前节点,一个指针pa指向其父节点。 - 如果
cur节点在pa的左子树中,那么这个pa节点的平衡因子减一,否则加一。 - 更新平衡因子之后,观察
pa平衡因子大小。如果为0,则说明当前pa节点向上的所有父节点的平衡因子都不会改变。 - 如果·pa·平衡因子为-1或者1,则说明当前节点符合平衡二叉树节点特征,但是其父节点还不一定,于是继续向上遍历。
- 如果
pa平衡因子为2或者-2,则说明当前节点失衡了(左右子树的高度差大于1)!我们需要调整。
调整方案具体如下:
右单旋
如果cur的平衡因子为-1,且pa的平衡因子为-2。那么我们选择让pa节点右单旋。
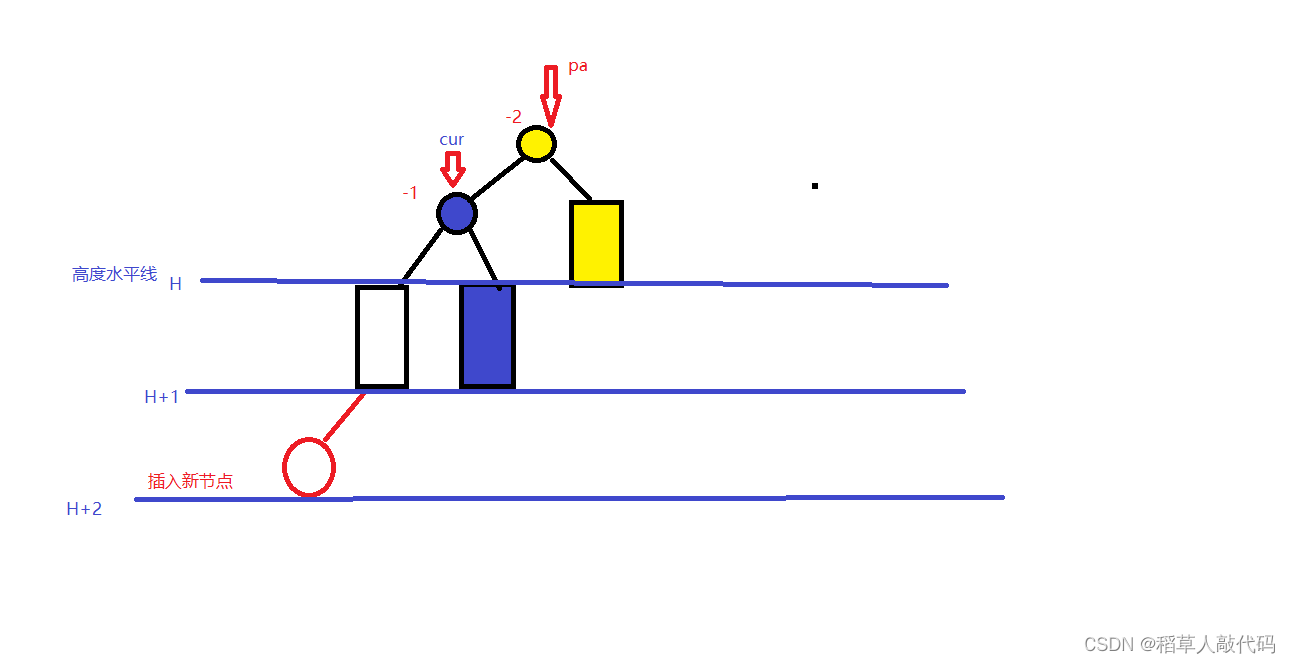
上图就是这种情况**。矩形表示一颗子树**。右旋过之后就变成了这样:
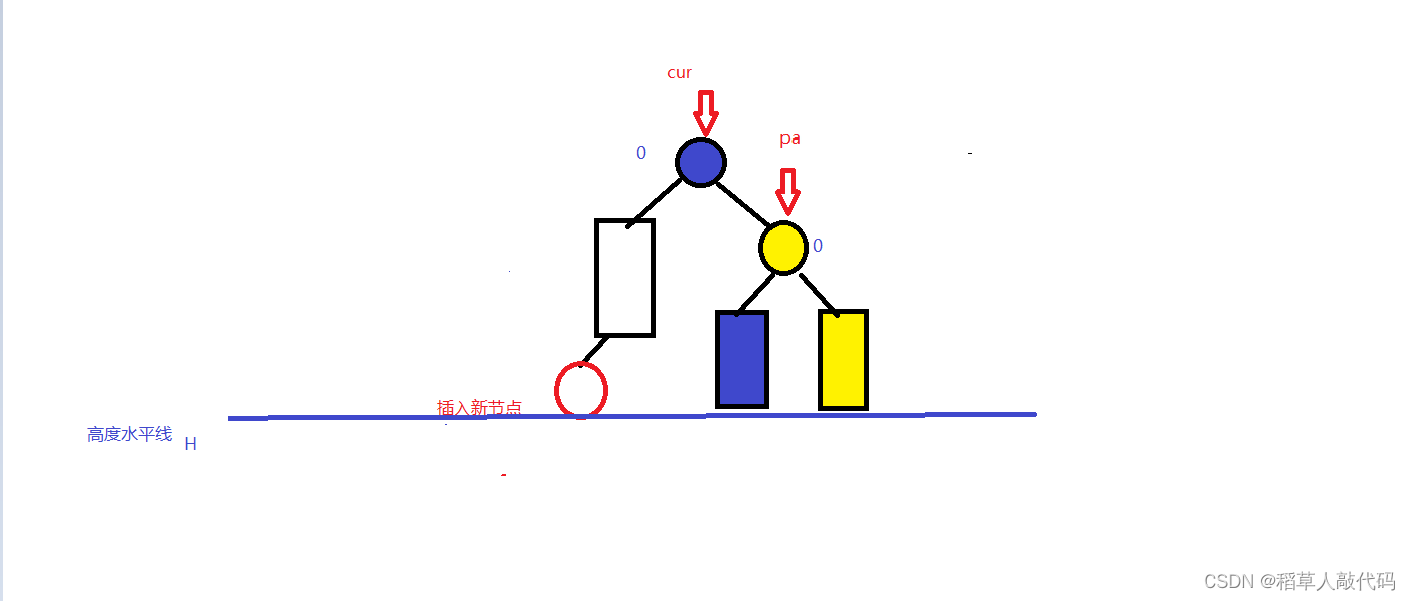
为什么要右单旋呢?
或者说为什么右单旋之后,pa和cur的平衡因子会为0呢?
假设在没有旋转的时候,pa的左子树高度为N,则右子树高度为N-2。即上图黄色矩形的表示的树的高度为N-2。
由于cur的平衡因子为-1,则cur左子树的高度为N-1,右子树的高度为N-2。即上图蓝色矩形表示的树的高度为N-2。所以,我们完成这样一个右单旋之后,对于
cur来说,左子树的高度依旧是N-1,但是右子树的高度变成了N-1,平衡因子也就变成了0。
对于pa来说,它的右子树高度依旧是N-2,但是左子树高度变成了N-2,平衡因子也变成了0。
右单旋之后还需不需要继续往上调整呢呢?答案是不用了,由于cur和pa的平衡因子都是0了,再往上的节点的平衡因子保持不变。
继续思考,平衡因子是没问题了,但是这样旋转会不会改变二叉搜索树的性质呢?答案也是不会的。所谓的右单旋,就是把pa变成cur的右孩子,原本cur是pa的左孩子,pa节点包括pa的右子树的值均大于以cur子树的值。旋转之后cur的左子树的值依旧小于cur节点的值,cur右子树的值依旧大于cur节点的值。对于pa来说也是如此。
右单旋代码
//右单旋
void RotateR(pNode pa) {
pNode subL = pa->left;
pNode subLR = subL->right;
pa->left = subLR;
if (subLR) subLR->father = pa;
subL->right = pa;
pNode ppa = pa->father;
pa->father = subL;
if (pa == _root) {
_root = subL;
subL->father = nullptr;
}
else {
if (pa == ppa->left) {
ppa->left = subL;
}
else {
ppa->right = subL;
}
subL->father = ppa;
}
subL->_bf = pa->_bf = 0;
}
左单旋
如果cur的平衡因子为1,且pa的平衡因子为2。那么我们选择让pa节点左单旋。
在理解右单旋的原理之后,对于左单旋也就容易理解了,因为两者的旋转方式都是一样的,只不过“方向”不同。
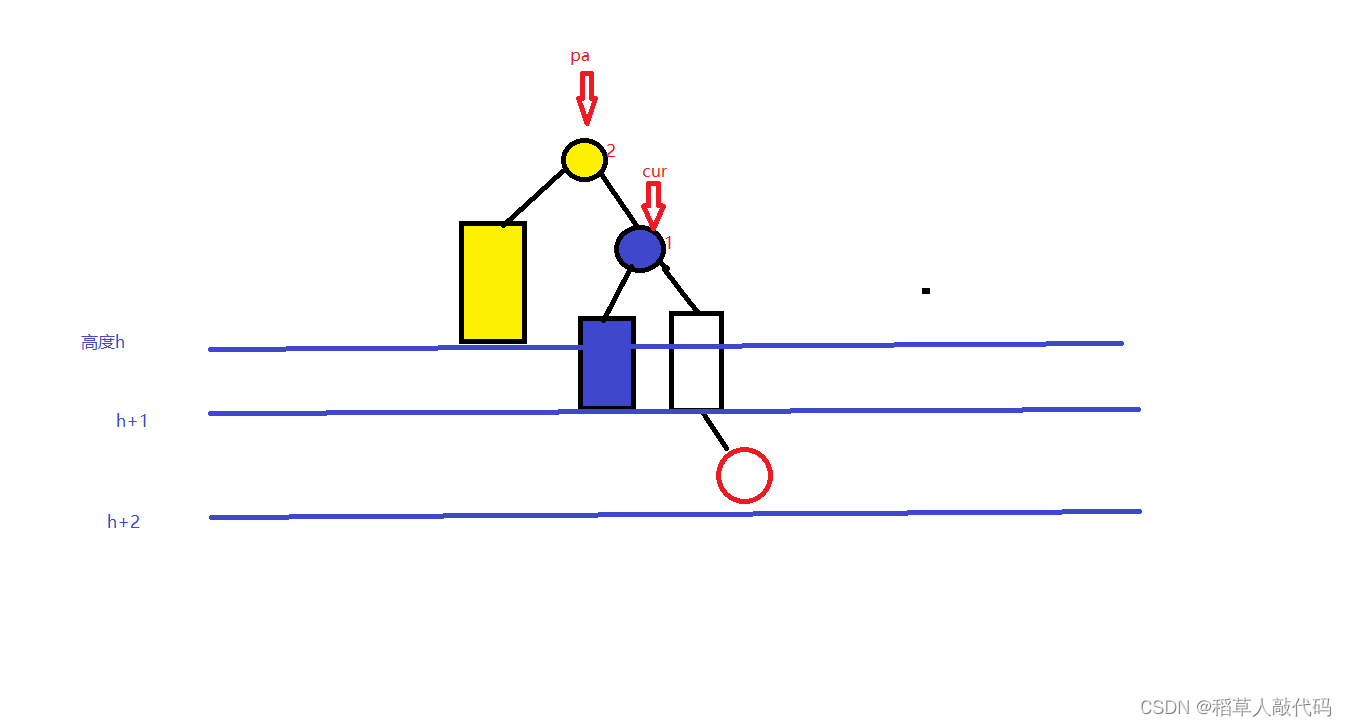
这种情况我们就需要对pa进行左单旋,调整之后就变成了下图所示:
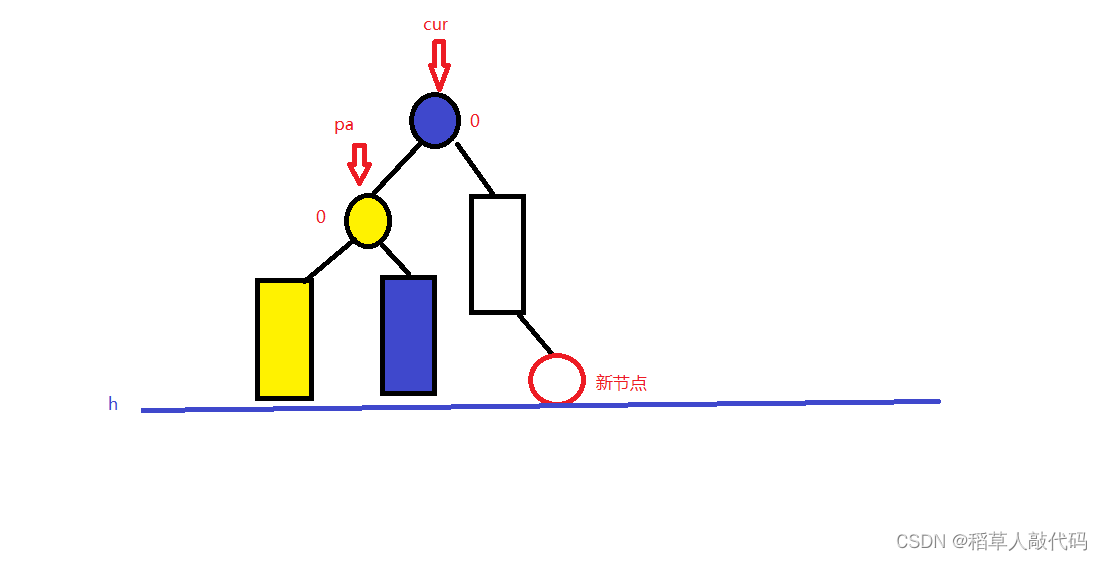
为什么要左单旋?
参考右单旋。
假设在没有旋转的时候,pa的左子树高度为N,则右子树高度为N+2。即上图黄色矩形的表示的树的高度为N。
由于cur的平衡因子为1,则cur右子树的高度为N+1,左子树的高度为N。即上图蓝色矩形表示的树的高度为N。所以,我们完成这样一个左单旋之后,对于
cur来说,右子树的高度依旧是N+1,但是左子树的高度变成了N+1,平衡因子也就变成了0。
对于pa来说,它的左子树高度依旧是N,但是右子树高度变成了N,平衡因子也变成了0。
左单旋代码
//左单旋
void RotateL(pNode pa) {
pNode subR = pa->right;
pNode subRL = subR->left;
pa->right = subRL;
if (subRL) subRL->father = pa;
subR->left = pa;
pNode ppa = pa->father;
pa->father = subR;
if (pa == _root) {
_root = subR;
subR->father = nullptr;
}
else {
if (pa == ppa->left) {
ppa->left = subR;
}
else {
ppa->right = subR;
}
subR->father = ppa;
}
subR->_bf = pa->_bf = 0;
}
左右双旋
如果cur的平衡因子为1,且pa的平衡因子为-2。那么我们选择先让pa节点的左孩子左单旋。然后再让pa右单旋。
这种情况只对pa进行右单旋不能保证让所有节点平衡,我们自能
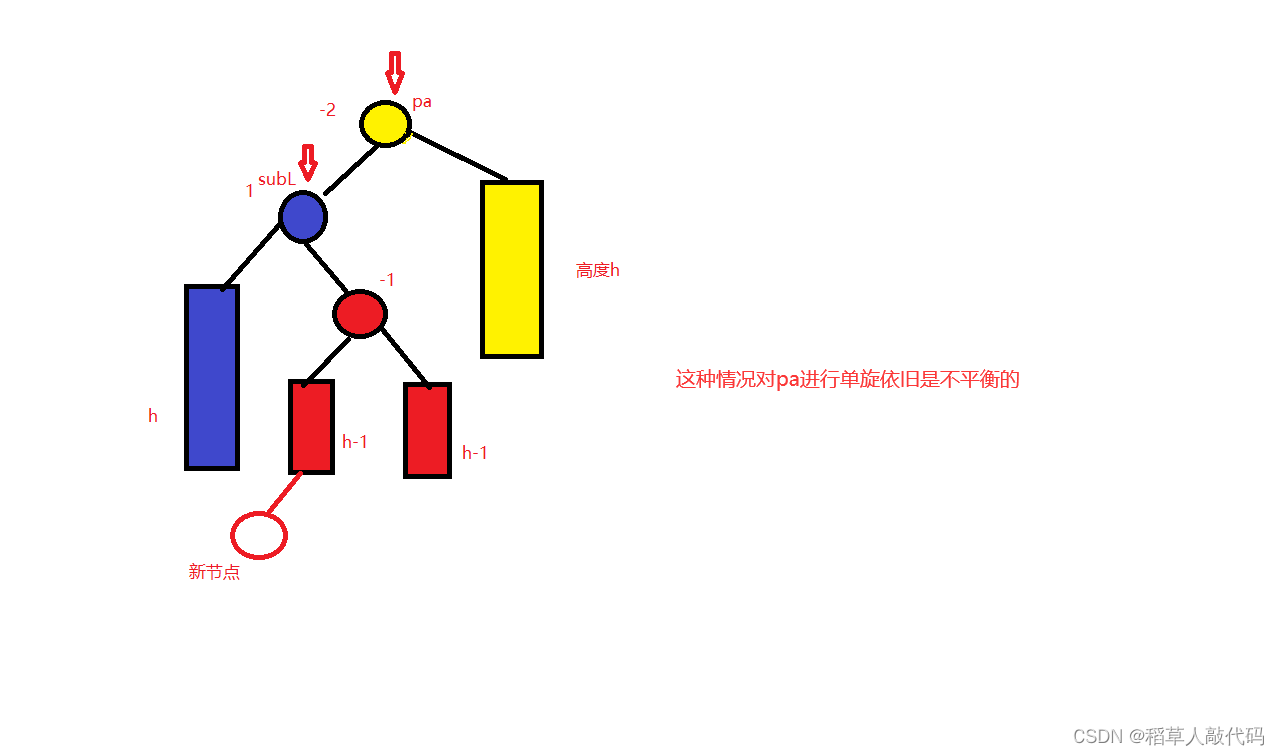
图中的h表示子树的高度
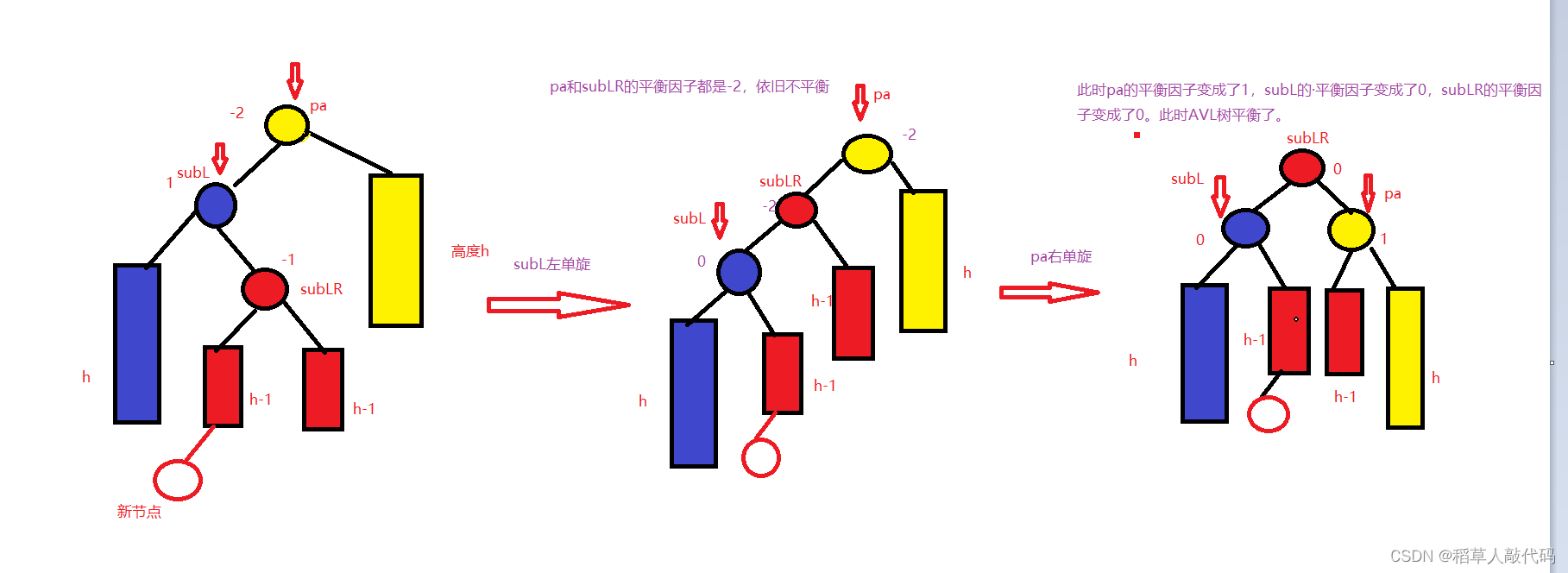
仔细观察上图AVL树左右双旋的过程,就能明白为什么要双旋能让每个节点再次平衡了。值得注意的是,在双旋之后,pa于subL节点的平衡因子并不是固定的,它们随着新节点插入到subLR的位置的而变化。
例如:
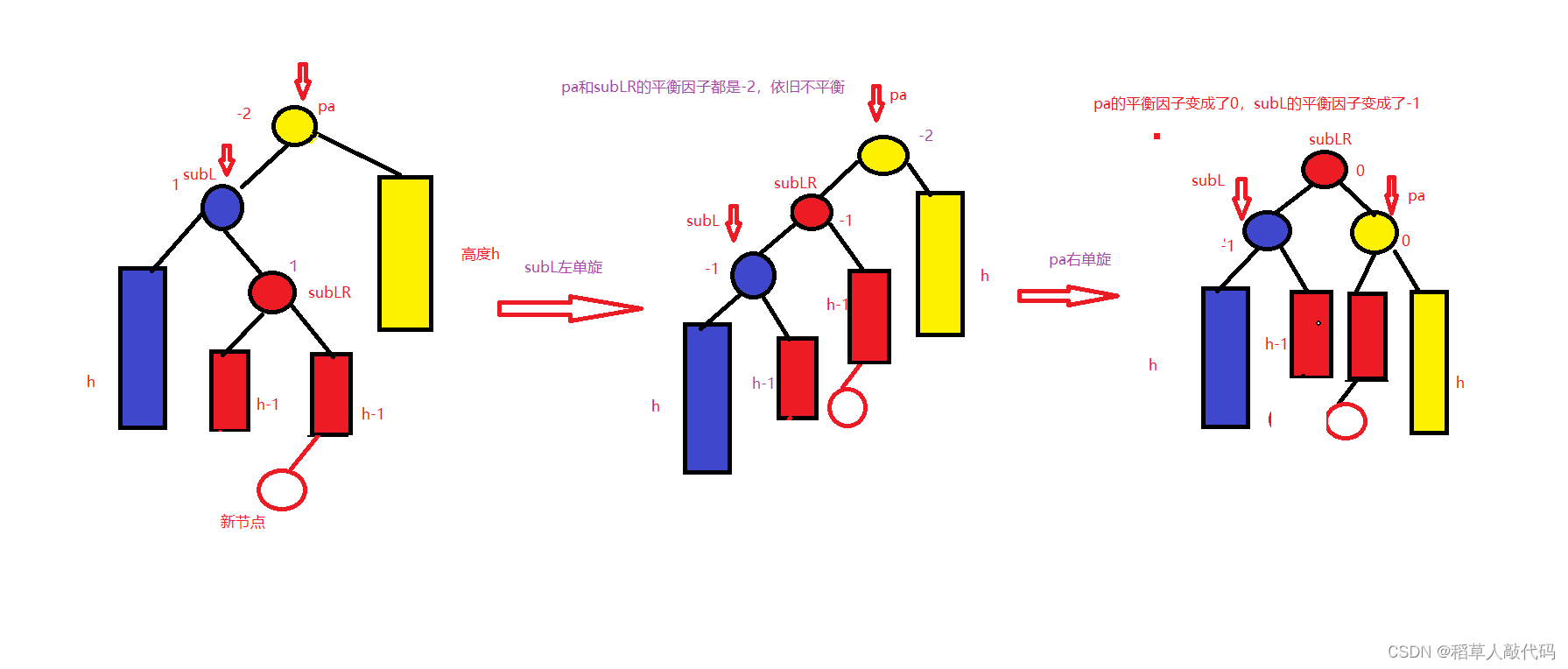
左右双旋之后平衡因子的情况
- 情况(1)如果新节点插入到subLR的左子树中,在双旋之后,这个新节点会变成subL的右子树节点,此时subL的平衡因子为0,pa的平衡因子为1。
- 情况(2)如果新节点插入到subLR的右子树中,双旋之后,这个新结点则会变成pa的左子树节点,此时pa的平衡因子为0,subL的平衡因子为-1。
- 情况(3)如果新插入节点本身就是subLR节点,即此时subLR的平衡因子为0。也就意味着双旋之后,pa和subL的平衡因子为0.
- 但无论是上面的哪种情况,双旋之后,subLR的平衡因子都是0.
那更新pa和subL的平衡因子时如何区分是以上哪种情况呢?看subLR的平衡因子。如果是-1,表示新节点在subLR的左子树中,即情况(1)。如果是1,说明新节点在subLR的右子树中,即情况(2)。如果是0,表示新节点就是subLR本身,即情况(3)。
左右双旋代码实现
有了上面左右单旋的代码,左右双旋就能通过使用封装它们的函数来实现了:
//左右双旋
void RotateLR(pNode pa) {
pNode subL = pa->left;
pNode subLR = subL->right;
int subLR_bf = subLR->_bf;
RotateL(subL);
RotateR(pa);
if (subLR_bf == -1) {
pa->_bf = 1 ;
subL->_bf = 0;
}
else if (subLR_bf == 1) {
pa->_bf = 0;
subL->_bf = -1;
}
else if (subLR_bf == 0) {
pa->_bf = 0;
subL->_bf = 0;
}
else {
//perror("RotateLR");
}
return;
}
右左双旋
如果cur的平衡因子为-1,且pa的平衡因子为2。那么我们选择先让pa节点的右孩子右单旋。然后再让pa左单旋。
原理和左右双旋一致,只不过旋转的方向相反:
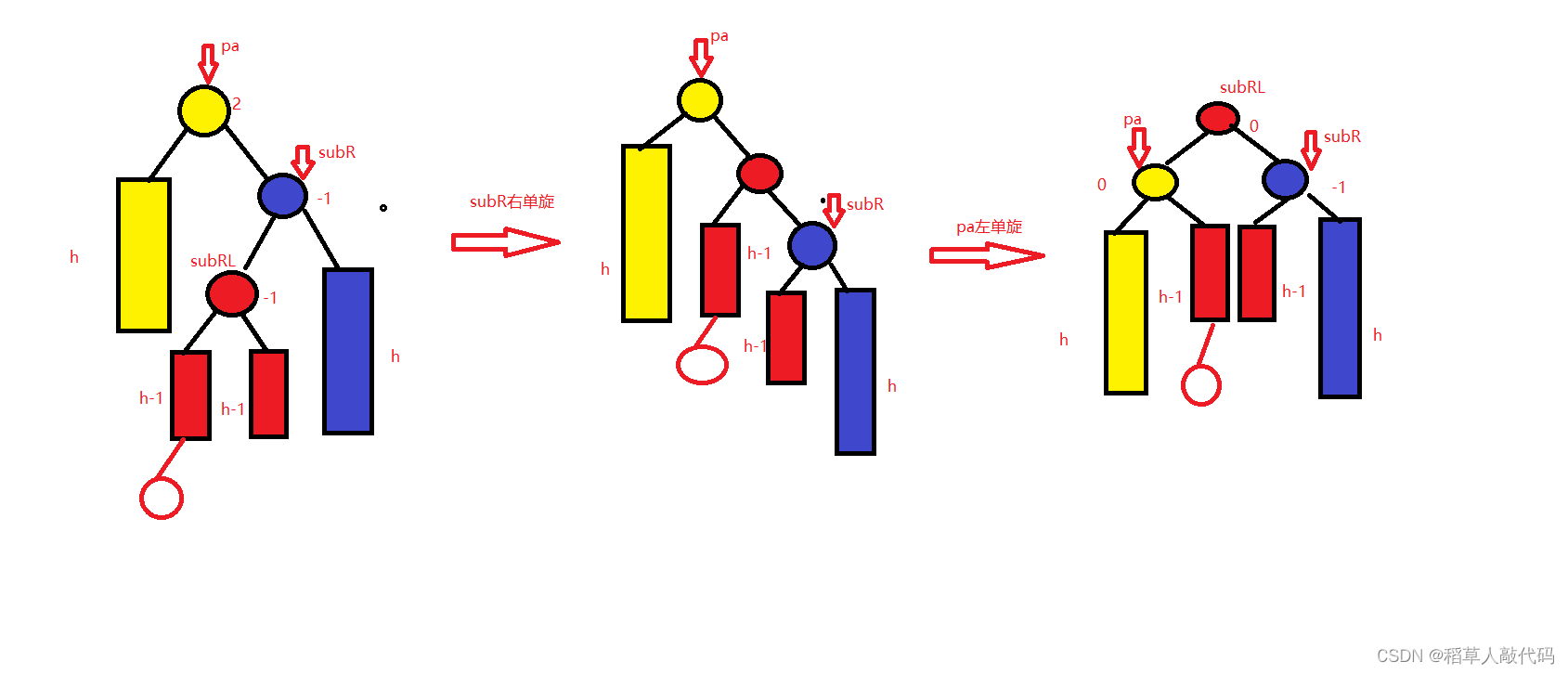
右左双旋的平衡因子的情况参考左右双旋,我这里就不做过多赘述了。
同样右左双旋的代码可以使用单旋的接口来实现
右左双旋代码:
//右左双旋
void RotateRL(pNode pa) {
pNode subR = pa->right;
pNode subRL = subR->left;
int subRL_bf =subRL->_bf;
RotateR(subR);
RotateL(pa);
if (subRL_bf == -1) {
pa->_bf = 0;
subR->_bf = 1;
}
else if (subRL_bf == 1) {
pa->_bf = -1;
subR->_bf = 0;
}
else if (subRL_bf == 0) {
pa->_bf = 0;
subR->_bf = 0;
}
else {
//perror("RotateRL");
}
}
简单测试
通过上面的学习,现在我们就能基本实现AVL树的插入操作了。为了检查代码的正确性,下面给出一组测试数据插入到AVL树中,并遍历输出观察结果:
#include<iostream>
#include"myAVLTree.h"
using namespace std;
using namespace k_val;
int main() {
int a[10] = { 1,7,8,3,4,9,10,2,6,5 };
AVLTree<int, int> avl;
for (int i = 0; i < 10; i++) {
avl.Insert({ a[i],a[i] });
}
avl.InOrder();
return 0;
}
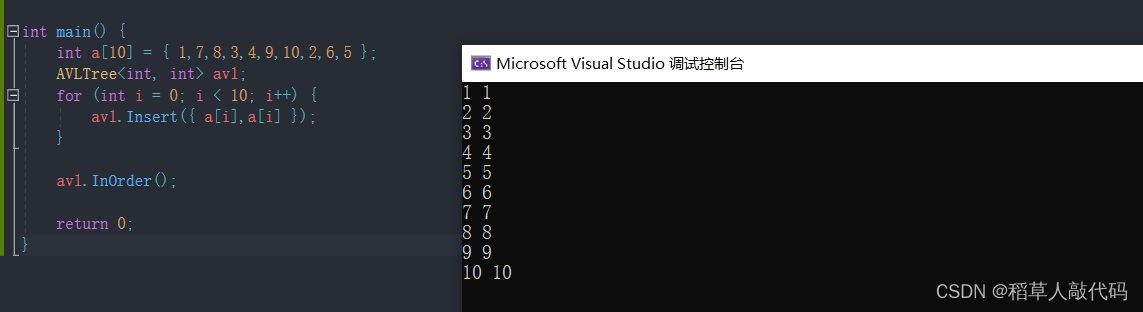
如果想观察·内部结构,可以自行打开调试窗口一一查看。