第三章 动态规划法
目录
●第三章 动态规划法
●前言
●一、动态规划法是什么？
1.简要介绍
2.生活实例
●二、动态规划法对斐波那契数列的优化
1.优化方法
2.优化核心代码片段
3.代码实现以及结果展示
●三、动态规划法的典型案例——最短总距离
1.具体情况
2.代码展示（C++）
3.代码结果展示
●总结
前言
简单的来说，算法就是用计算机程序代码来实现数学思想的一种方法。学习算法就是为了了解它们在计算机中如何演算，以及在当今的信息时代，它们是如何在各个层面上影响我们的日常生活的，从而提高我们的逻辑思维能力和处理实际问题的能力。善用算法、巧用算法，是培养程序设计逻辑的重中之重，许多实际的问题都可用多个可行的算法来解决， 但是要从中找出最优的解决算法却是一项挑战。
一、动态规划法是什么？
1.简要介绍
20世纪50年代初，动态规划法由美国数学家R.E.Bellman所创造，它很类似于分治法并且用来研究多阶段决策问题的优化过程和对问题最优解的求法。动态规划法的核心做法：如果一个问题的答案与子问题相关的话，就能将这个大问题拆解成多个子问题，并且将每个子问题的答案储存起来用于下一次求解时的直接使用。它与分治算法最大的不同点就是在于子问题能否去进行存储的问题。
2.生活实例
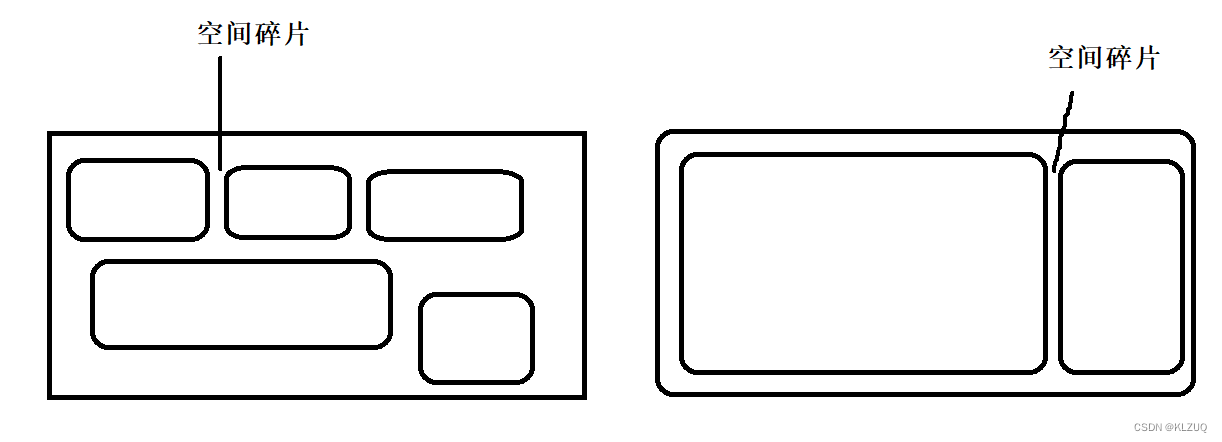
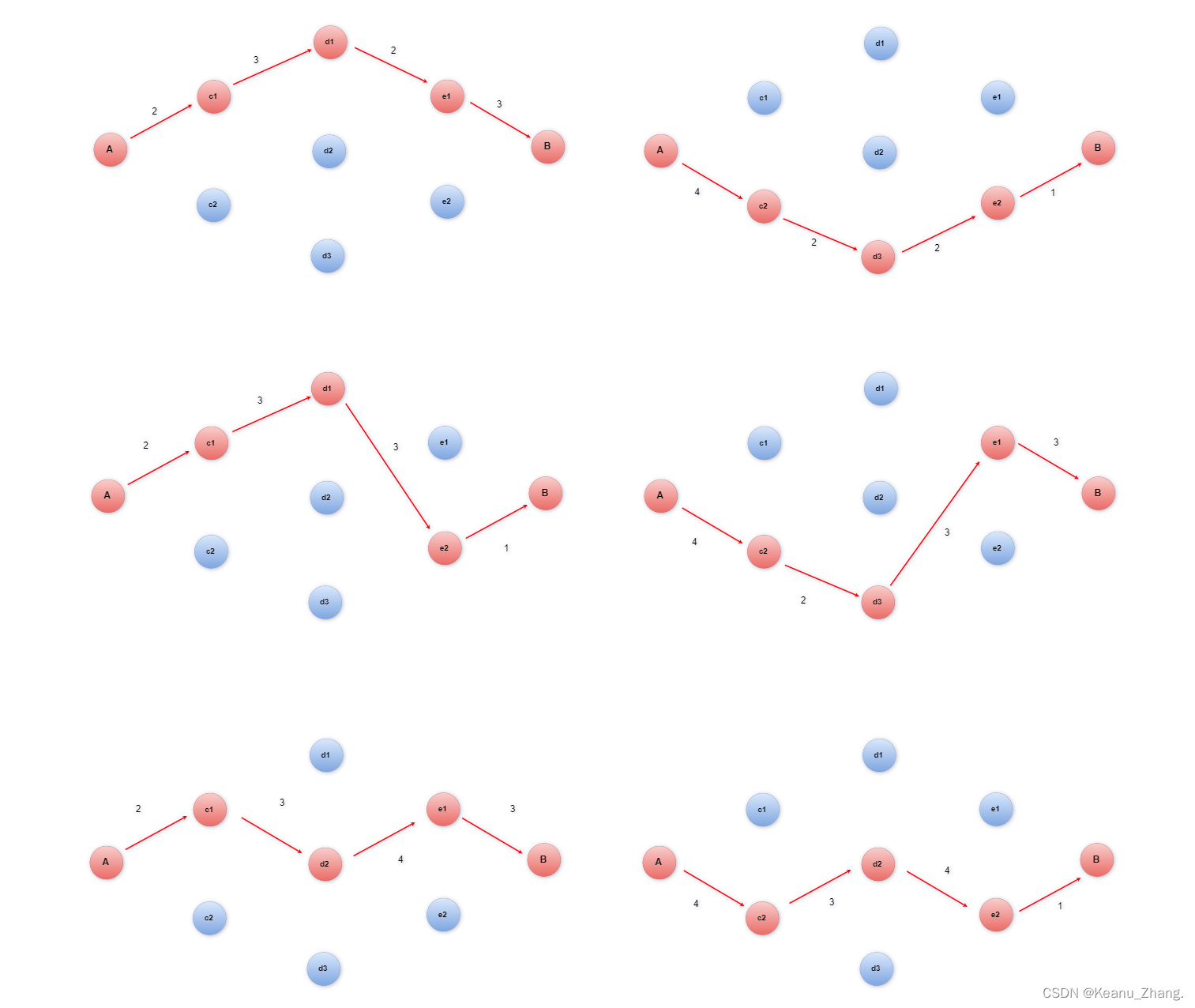
① 一个工程队需要从一个地方往另一个地方修建下水管道。他们的出发地是A，目的地是B，其中有三级中间站（中转枢纽），两地之间的连线表示即将要修建的下水管道，并且每一级的枢纽只能与自己下一级所有的枢纽相连，而不能跨级相连（具体情况如图所示）。工程队要从总的计划方案中找出最短的路径，从而以较低的成本去完成此次任务。 
运用动态规划的思想对该次任务进行分析：我们的总计划方案可以规划成多种子方案，并且每种情况下的子方案还与原来总方案之间是具有相关的关系的，是它的子问题。将每种情况下子方案的路径算出并记录下来，最终进行方案的总体比较从而得出我们要找的最短路径。
二、动态规划法对斐波那契数列的优化
1.优化方法
从第二章（http://t.csdn.cn/4OxrH）我们讲解的斐波那契函数执行路径图中可知，它递归调用了多次，加法也运算了多次。这样的重复计算影响到了执行的性能和效率，根据动态规划的思想已经计算过的数据就不需要再去重复计算，也不必要再往下递归。从而我们将对它进行以下的优化：
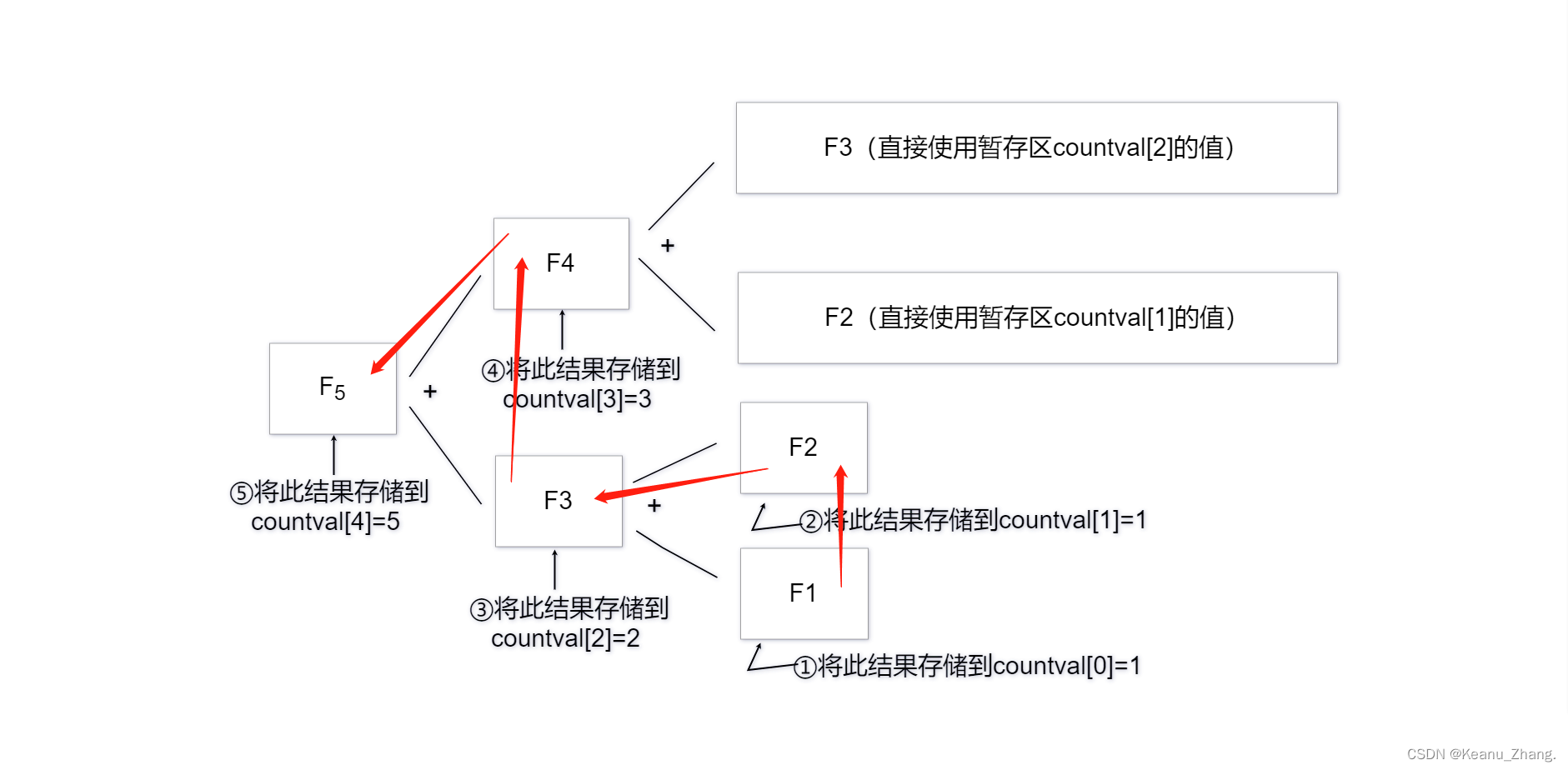
前面介绍中我们提到过，动态规划法的核心就是将已经计算过的数据进行记录存储。为了达到这个目的，我们可以先去设置一个用来记录值的数组countval，该数组中的每一个值将会去记录已经被计算过的斐波那契数列中的各项值，并且在记录前需要将该数组设为空。每当下一次要去计算斐波那契数列中的值时，就先去从countval中去判断，如果是空值就去继续进行计算，再将计算所得结果保存到相应下标的数组中......具体过程如下：
①第一次计算F1，按照斐波那契数列定义，其数值为1，将此值存入暂存区countval[0]中；
②第一次计算F2，按照斐波那契数列定义，其数值为1，将此值存入暂存区countval[1]中；
③第一次计算F3，按照斐波那契数列定义，其数值为F1+F2，即countval[0]+countval[1]=2，再将F3的值存入暂存区countval[2]中；
④第一次计算F4，按照斐波那契数列定义，其数值为F2+F3，即countval[1]+countval[2]=3，在将F4的值存入暂存区countval[3]中；
⑤第一次计算F5，按照斐波那契数列定义，其数值为F3+F4，即countval[2]+countval[3]=5，
再将F5的值存入暂存区countval[4]中，结束执行。
2.优化核心代码片段
int countval[1000] = { 0 }; //暂存区
int Fib(int n)
{
int result;
result = countval[n-1];
if (result == 0)
{
if (n == 1 || n == 2) {
result = 1;
}
else {
result = Fib(n - 2) + Fib(n - 1);
}
countval[n-1] = result;
}
return result;
}3.代码实现以及结果展示
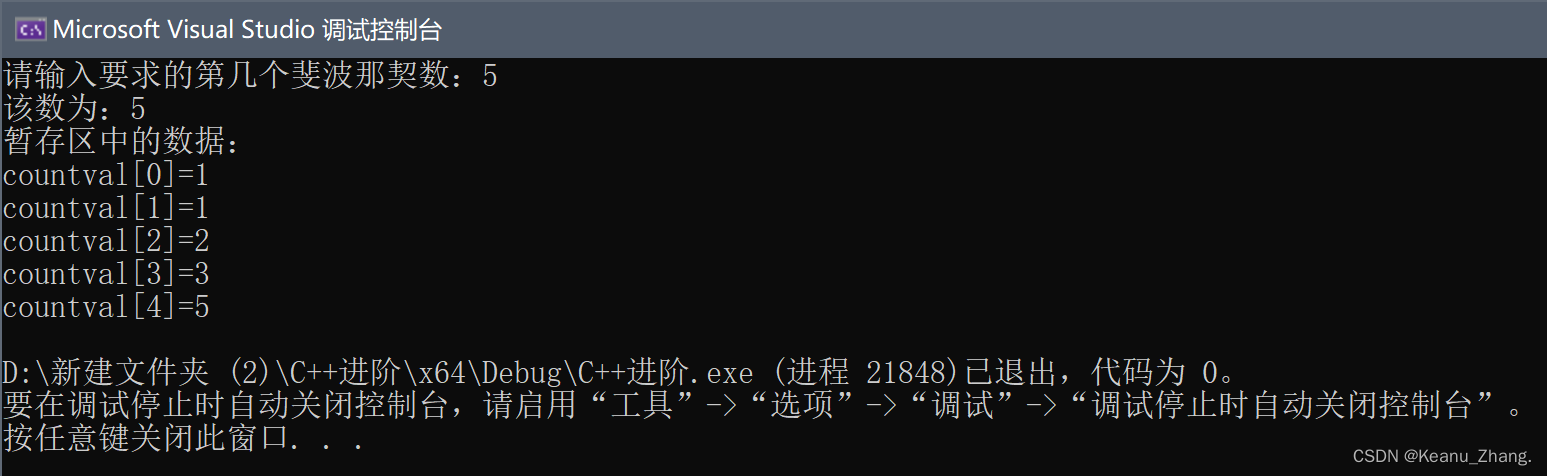
用优化后的方法去求解第五个斐波那契数的值，并且输出暂存区中的存储数据。
#include<iostream>
using namespace std;
int countval[1000] = { 0 }; //暂存区
int Fib(int n)
{
int result;
result = countval[n-1];
if (result == 0)
{
if (n == 1 || n == 2) {
result = 1;
}
else {
result = Fib(n - 2) + Fib(n - 1);
}
countval[n-1] = result;
}
return result;
}
void text()
{
int i = 0;
cout << "请输入要求的第几个斐波那契数：";
int x; cin >> x;
cout << "该数为：" << Fib(x) << endl;
cout << "暂存区中的数据：" << endl;
while (countval[i] != 0)
{
cout << "countval" << "[" << i << "]" << "=" << countval[i] << endl;
i++;
}
}
int main()
{
text();
}
三、动态规划法的典型案例——最短总距离
1.具体情况
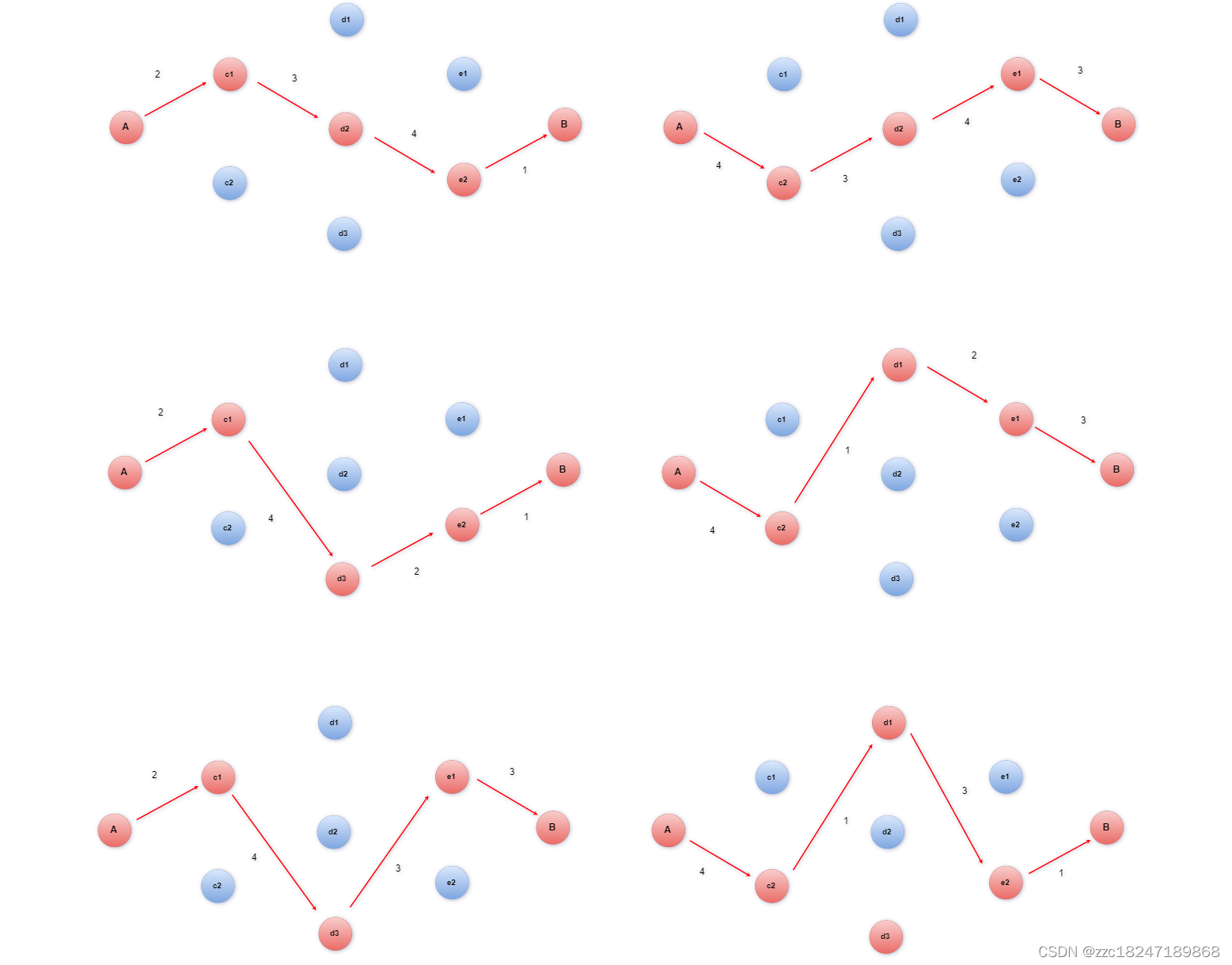
要在某地区5个城市之间去修路，将这5座城市构成一幅交通图，并且要使修的路的总距离要最短。因此对总体方案进行如下分析：
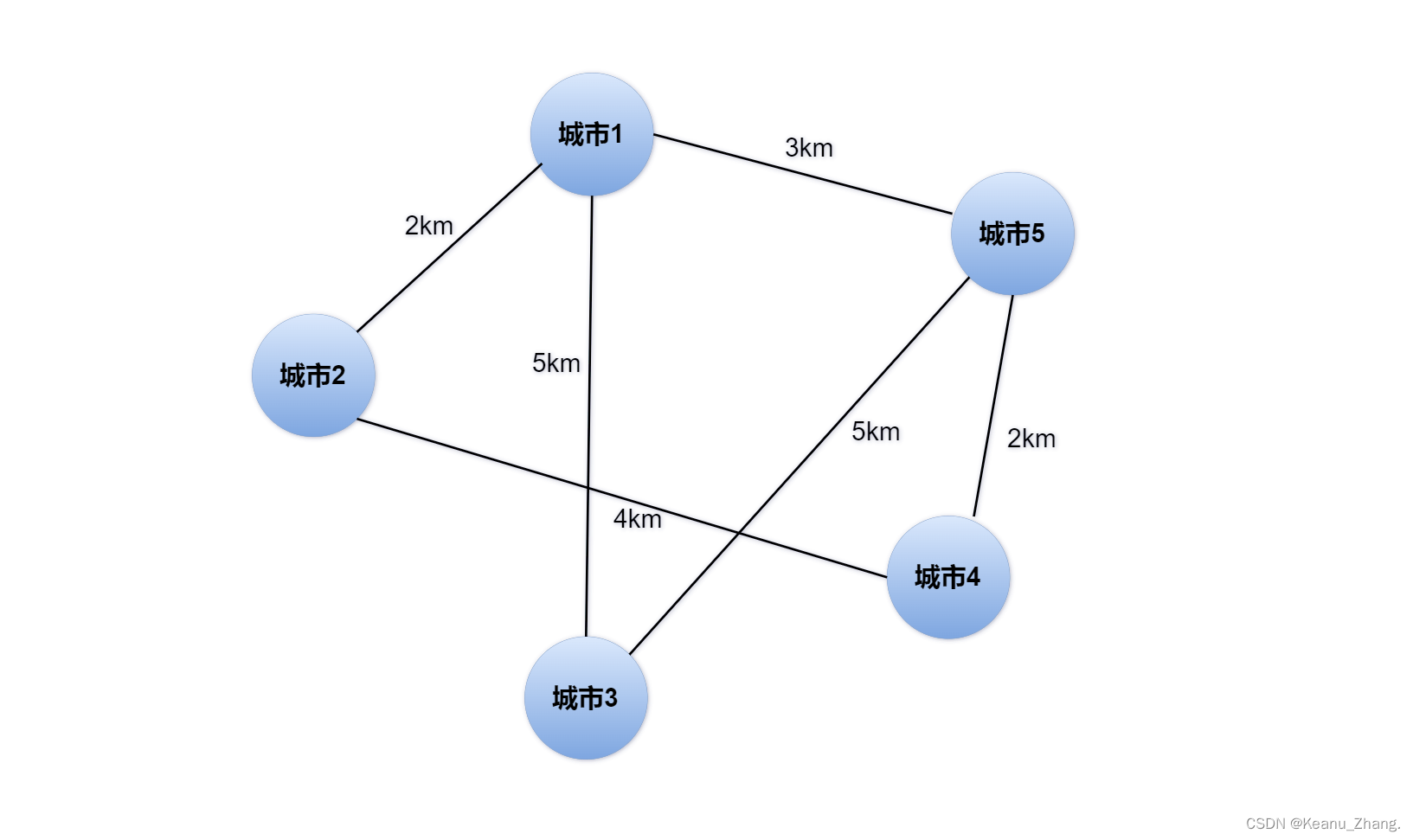
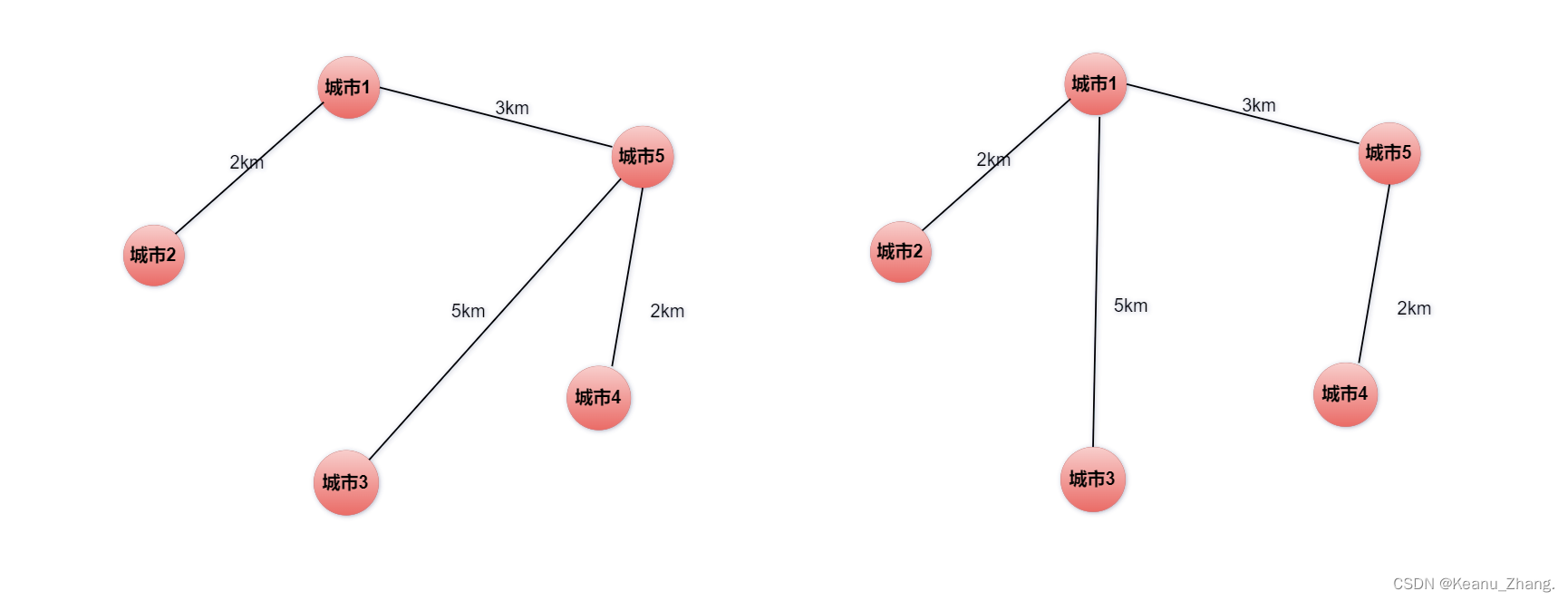
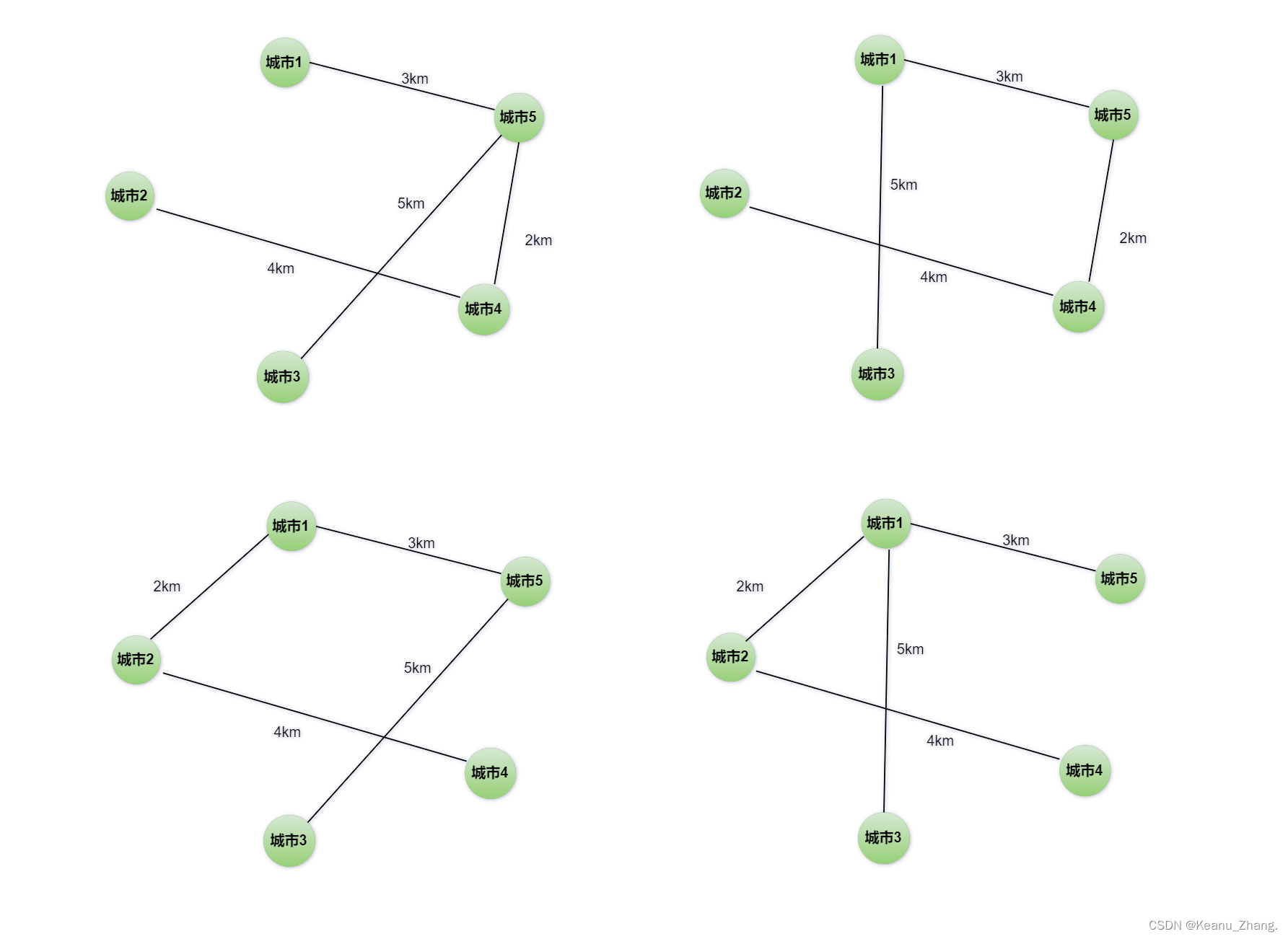
从上面各种情况中我们分析可知，情况一和情况二中子图的顶点和总体方案原图完全相同。子图的分支也是总体方案原图的子集，这些子分支刚好将图中所有城市连接起来，形成一张交通图。
2.代码展示（C++）
使用程序代码去构建以上的具体情况，并且求解出最短路径的具体长度。
#include<iostream>
using namespace std;
#define maxnum 20 //自定义图的最大的顶点数
#define maxvalue 65535
#define yes 0 //已选用顶点
#define no -1 //非邻接顶点
typedef struct {
char vertex[maxnum]; //顶点信息
int g_type; //图的类型
int vertex_num; //顶点的数量
int edge_num; //边的数量
int edge_weight[maxnum][maxnum]; //边的权
}graphmatrix;
void creategraph(graphmatrix& gm)
{
int weight; //权重
char start_vertex, end_vertex; //起始两顶点
int i,j,k;
cout << "###请输入图中各顶点信息###" << endl;
for (i = 0; i < gm.vertex_num; i++)
{
cout << "第" << i + 1 << "个城市:";
cin >> gm.vertex[i];
}
cout << "###请输入图中构成各边的左右顶点以及该边的权值###" << endl;
for (k = 0; k < gm.edge_num; k++)
{
cout << "第" << k + 1 << "条边:";
cin >> start_vertex >> end_vertex >> weight;
for (i = 0; start_vertex != gm.vertex[i]; i++) //查找始点
{
for (j = 0; end_vertex != gm.vertex[j]; j++) //查找终点
{
gm.edge_weight[i][j] = weight; //找到后将权值保存
}
}
if (gm.g_type == 0)
{
gm.edge_weight[j][i] = weight;
}
}
}
void clear_graph(graphmatrix& gm)
{
for (int i = 0; i < gm.vertex_num; i++)
for (int j = 0; j < gm.vertex_num; j++)
gm.edge_weight[i][j] = maxvalue;
}
void min_graph(graphmatrix &gm)
{
int min, sum=0;
int weight[maxnum];
char vertex_[maxnum];
int k;
for (int i = 1;i< gm.vertex_num; i++)
{
weight[i] = gm.edge_weight[0][i]; //保存邻接矩阵中的一行数据
if (weight[i] == maxvalue)
vertex_[i] = no;
else
vertex_[i] = gm.vertex[0];
}
vertex_[0] = yes;
weight[0] = maxvalue;
for (int i = 1; i < gm.vertex_num; i++)
{
min = weight[0];
k = i;
for (int j = 1; j < gm.vertex_num; j++)
{
if (weight[j] < min && vertex_[j]>0) //寻找具有更小权值的边
{
min = weight[j];
k = j;
}
}
sum += min; //将权值进行累加
vertex_[k] = yes;
weight[k] = maxvalue;
for (int j = 0; j < gm.vertex_num; j++)
{
if (gm.edge_weight[k][j] < weight[j] && vertex_ != 0)
{
weight[j] = gm.edge_weight[k][j];
vertex_[j] = gm.vertex[k];
}
}
}
cout << endl;
cout << "最短路径的总长度为：" << sum << endl;
}
void text()
{
graphmatrix gm;
cout << "###创建图###" << endl;
cout << "输入图的类型（0:无向图 1:有向图）:";
cin >> gm.g_type;
cout << "输入图中城市的数量:";
cin >> gm.vertex_num;
cout << "输入图中城市间路径的数量:";
cin >> gm.edge_num;
clear_graph(gm);
creategraph(gm); //构建图
min_graph(gm); //最小生成树算法 ,动态规划的使用块
}
int main()
{
text();
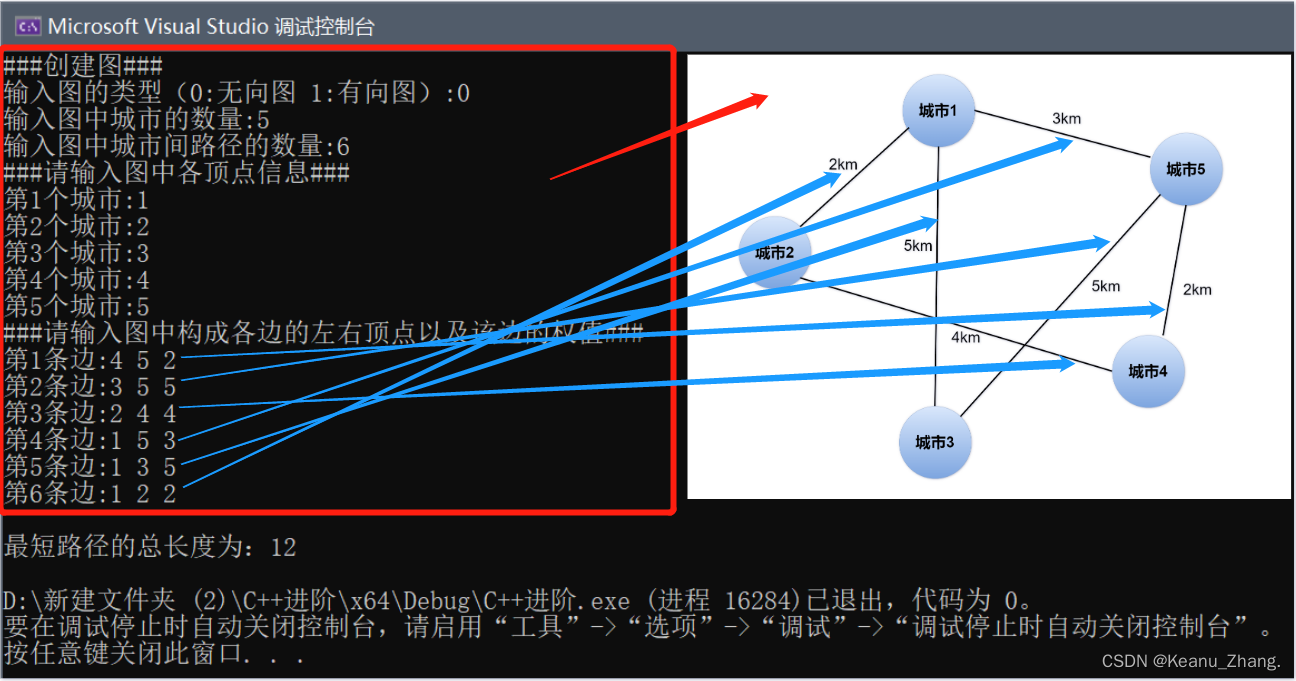
}3.代码结果展示
总结
在上面我们通过通俗易懂的例子对动态规划法进行了理解，也用该方法的核心对斐波那契数列进行了优化。动态规划是分治法的一个延伸，它增加了记忆机制的使用，将处理过的子问题的答案记录下来，从而避免去重复计算。
<您的三连和关注是我最大的动力>
🚀 文章作者：Keanu Zhang 分类专栏：算法之美（C++系列文章）
