题目描述
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。
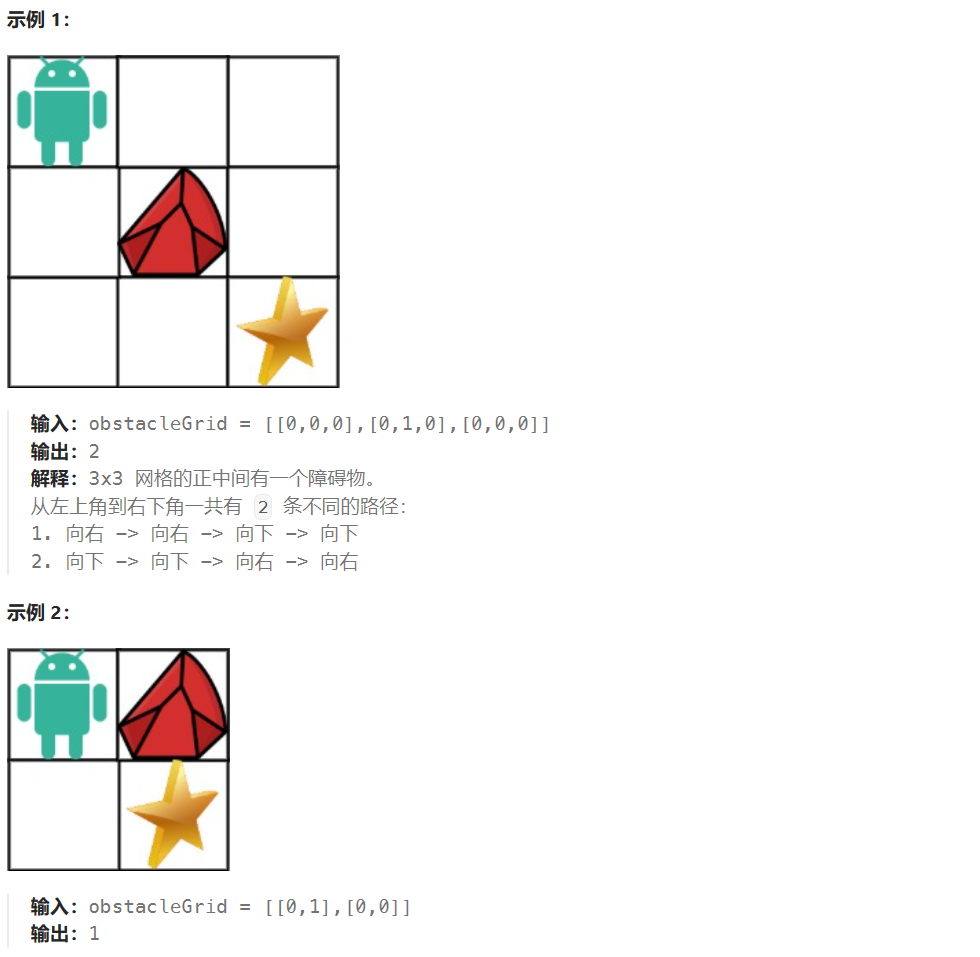
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
网格中的障碍物和空位置分别用 1 和 0 来表示。
代码
class Solution {
public:
/*
dp[i][j]:从[0,0]到[i,j]的路线数
递推公式:if(obs[i][j] == 0) 相当于将障碍物所在的位置 dp[i][j]的值为0
dp[i][j] = dp[i-1][j] + dp[i][j-1]
初始化: dp[0][i] = 1,如果遇到dp[0][i]为障碍物,则break,因为后面都到达不了
dp[i][0]类似
*/
int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
int m = obstacleGrid.size();
int n = obstacleGrid[0].size();
vector<vector<int>> dp(m, vector<int>(n, 0));
//初始化第一列
for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) {
dp[i][0] = 1;
}
//初始化第一行
for (int i = 0; i < n && obstacleGrid[0][i] == 0; i++) {
dp[0][i] = 1;
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
if (obstacleGrid[i][j] == 0)
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m - 1][n - 1];
}
};





![NSSCTF | [SWPUCTF 2021 新生赛]easy_sql](https://img-blog.csdnimg.cn/direct/b0fd4213324c4236af4b354d318e9bf5.png)
![[蓝桥杯]真题讲解:抓娃娃(思维+二分)](https://img-blog.csdnimg.cn/direct/2ba8eed64b4f4d7088e1cbb8492570fc.png)