一、简单选择排序

void select_sort(int a[], int len){
//len为数组长度
	for (int i = 0; i < len-1; ++i){
	//n个数需要比较n-1趟
		int min = i;//记录最小值的位置
		for (int j = i+1; j <= len-1; j++){
			if (a[j] < a[min]) min = j;//更新最小值的位置
		}	
		if (min != i) swap(a[i], a[min]);
	}
}

动画演示请点击这里

算法思想：
在待排序的数据中选出最小或最大放在最终位置，类似于暴力打擂台

1、首先通过n-1次比较，找出最小元素，把它和第一个记录交换

2、再通过n-2次记录从剩余的n-1个记录中找出次小的元素，把它和第二小的记录交换

3、重复上述操作，共进行n-1趟排序后，排序结束

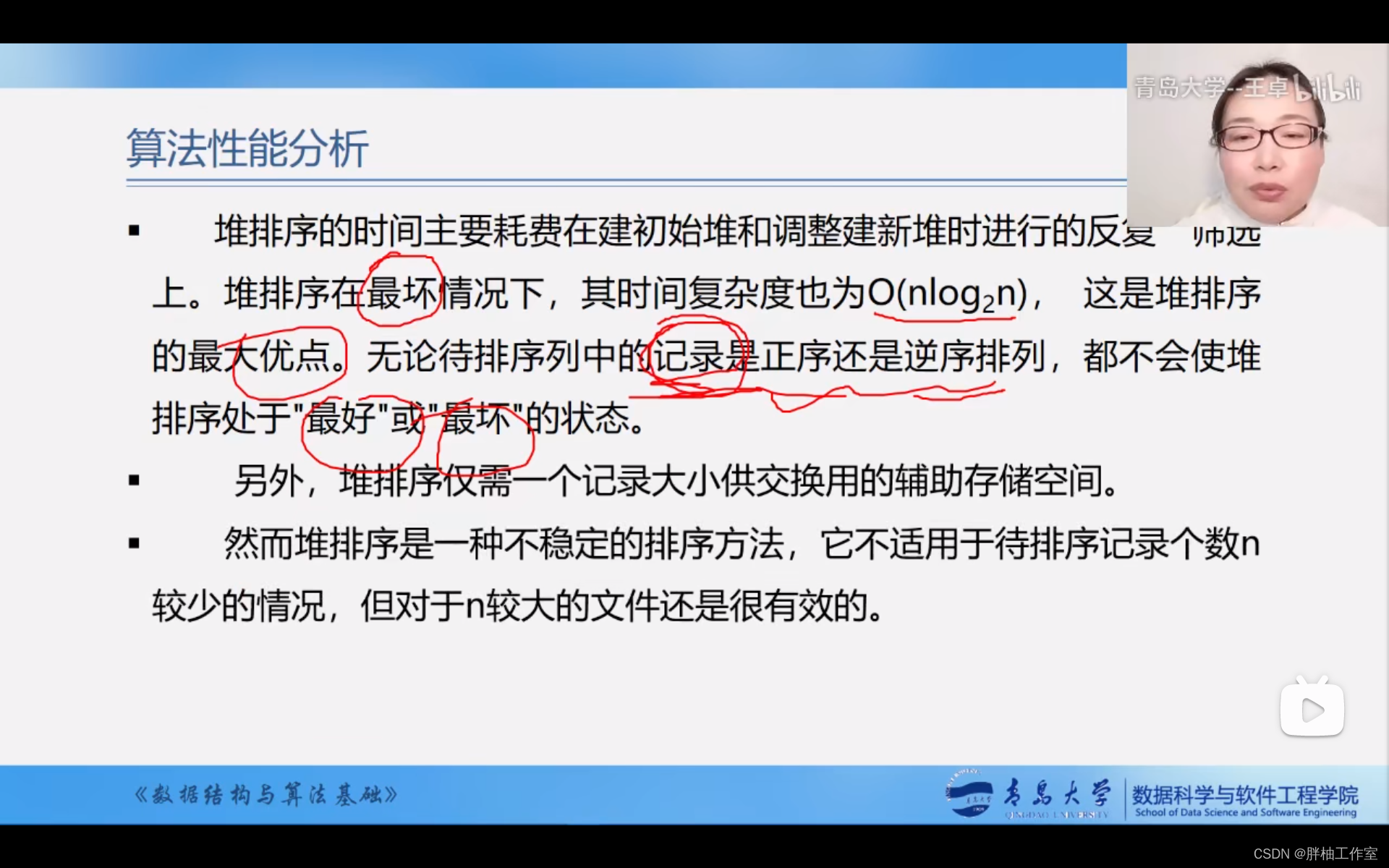
二、堆排序

从堆的定义可以看出，堆实质是满足如下性质的完全二叉树：二叉树中任一非叶子结点均小于（大于）它的孩子结点（完全二叉树有性质，i的左孩子是2i，右孩子就是2i+1）

堆排序：若在输出最小值（最大值）之后，使得剩余n-1个元素的序列重新又建成一个堆，则得到n个元素的次小值（次大值）…如此重复，便能得到一个有序序列，这个过程称为堆排序

——如何由无序序列建立一个堆

——如果在输出堆顶元素后，调整为一个新的堆

堆的调整:

1、输出堆顶元素，以堆中最后一个元素替代之

2、然后将根结点值和左右子树的值比较，并与其中小（大）者进行交换

3、重复上述操作，直到叶子结点，将得到新的堆，称这个从堆顶至叶子的调整过程为筛选

void HeapAdjust(elem R[], int s, int m) {
    /*已知R[s...m]中记录的关键字除R[s]之外均满足堆的定义，也就是说R[s]的左右孩子树都是堆，本函数调整R[s]的关键字，使得R[s...m]成为一个大根堆*/
    rc=R[s];
    for (j=2*s; j<=m; j*=2) {//沿key较大的孩子结点向下到该结点的左孩子结点
    	if (j<m&&R[j]<R[j+1]) j++;//j为key较大的记录的下标，右孩子大就到右孩子
        if (rc>=R[j]) break;//根大于两个孩子，满足大根堆定义，那不用操作了
        R[s]=R[j]; s=j;//rc应插入在位置s上
    }
    R[s]=rc;//插入
}

动画演示请点击这里

//堆的建立
//先按照乱序，构造完全二叉树，然后从最后结点开始依次向前调整为堆
for (i=n/2; i>=1; i--)
    HeapAdjust(R, i, n)
    
//堆排序算法如下
void HeapSort(elem R[]) {//对R[1]到R[n]进行堆排序
	int i;
    for (i=n/2; i>=1; i--) HeapAdjust(R, i, n);//建立初始堆
    for (i=n; i>1; i--) {//进行n-1趟排序
        visit(R[1]);//访问最大结点
        Swap(R[1], R[i]);//根和最后一个元素交换，访问过，可以把它放到尾巴去了，没用
        HeapAdjust(R, 1, i-1);//对R[1]到R[i-1]重新建堆
    }
}