概览

问题定义

拐点检测名为 change point detection，对于一条不平缓的时间序列曲线，认为存在一些时间点 $(t_1,t_2,...,t_k)$ ，使得曲线在这些点对应的位置发生突变，这些时间点对应的曲线点称为拐点，在连续的两个拐点之间，曲线是平稳的。

拐点检测算法的质量，通过算法输出拐点与实际观测到的拐点的差值绝对值除以样本数来评估。

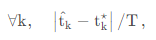
理想情况下，当样本数 T 无穷大时，误差应该减少到 0，这种性质称为满足渐近一致性 (asymptotic consistency.)

符号定义

$y_{a..b}$ 表示时间点 $a$ 和 $b$ 之间的时间序列，因此完整信号为 $y_{\mathrm{0..}T}$ 。

对于给定的拐点索引 $t$，它的关联分数 associate fraction 称为拐点分数 change point fractions ，公式为 ：

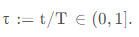
拐点分数的集合 $\tau ={\tau }_1,{\tau }_2,\dots$，写作 $|\mathbf{\tau }|$。

研究方法

一般思路是构造一个对照函数 contrast function，目标是将对照函数的值最小化。

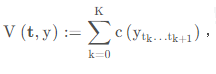
其中 $c(\cdot )$ 表示用来测量拟合度 goodness-of-fit 的损失函数 cost function，损失函数的值在均匀的子序列上较低，在不均匀的子序列上较高。

基于离散优化问题 discrete optimization problem，拐点的总数量记为 K ：

如果 K 是固定值，估算的拐点值为：

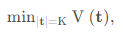
如果 $K$ 不是固定值，估算的拐点值为：

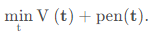
其中 $pen(t)$ 为对 $t$ 的惩罚项

在这种方法论下，拐点检测的算法包含以下三个元素：

1. 选择合适的损失函数来测算子序列的均匀程度 homogeneity，这与要检测的变化类型有关
2. 解决离散优化问题
3. 合理约束拐点的数量，确定使用固定的 K 还是用 pen() 来惩罚 penalizing 不固定的数量

损失函数