Matlab基础
- 1. Matlab界面与基本操作
- 1.1 matlab帮助系统
- 1.2 matlab命令
- 1.3 matlab功能符号
- 1.4 matlab的数据类型
- 1.5 函数计算
- 1.6 matlab向量
- 1.7 matlab多项式
- 1.8 M文件
- 1.9 函数文件
- 1.10 matlab的程序结构
- 1.11 echo、warning和error函数
- 1.12 交互输入
- 1.13 程序调试
- 1.14 设置断点调试
- 1.15 函数句柄 @
- 2. matlab中两种引号
- 3. matlab矩阵及运算
- 3.1 特殊变量
- 3.2多维矩阵
- 3.3 点乘与乘 = 幂运算
- 3.4 A*x=b求解
- 3.5 一个操作数是标量,而另一个操作上不是标量
- 3.6 矩阵元素的修改
- 3.7 常用矩阵函数
- 3.8 matlab符号运算
- 4. matlab的绘图
- 4.1 线图plot函数
- 4.1.2 三维曲线绘图 plot3
- 4.2 条形图bar函数
- 4.3 极坐标图polarplot函数
- 4.4 散点图scatter函数
- 4.5 三维曲面图surf
- 4.6 子图subplot函数
- 4.7 fplot精确绘图
- 4.8 ezplot符号函数绘图
- 4.9 plotyy 和 yyaxis
- 4.10 figure 创建图形窗口
- 4.11 坐标系与坐标轴axis
- 4.12 图形注释
- 4.13 文本属性
- 4.14 legend 添加图例
- 4.15 grid 坐标区网格线
- 4.16 area 区域图
- 4.17 pie饼图 和 histogram直方图
- 4.18 errorbar 含误差条的线图
- 4.19 stem 针状图
- 4.20 stairs 阶梯图
- 4.21 compass 罗盘图
- 4.22 quiver 箭头图
- 4.23 mesh 三维网格图
- 4.23.1 meshc 在网格图下展示等高线
- 4.23.2 meshz 在网格图下展示帷幕
- 4.24 三维网格ezmesh 和 三维曲面surf
- 4.25 cylinder 柱面
- 4.26 球面
- 4.27 contour3 等高线图
- 4.27.1 contourc等高线矩阵的计算
- 4.27.2 为等高线添加标签
- 4.28 三维图形的修饰处理
- 4.28.1 view 视角处理
- 4.28.2 brighten、caxis、colorbar 、shading、colormap颜色处理
- 4.28.3 光照处理surfl 和 light
- 5. matlab导入数据
- 6. matlab处理缺失值和异常值
- 7. 数模常用作图代码解析
- 7.1 二维曲线
- 7.2 二维散点图
- 7.3 scatter 二维渐变图
- 7.4 条形图
- 7.5 fill 填充图
- 7.6 多Y轴图
- 7.7 streamline 与 quiver 二维场图
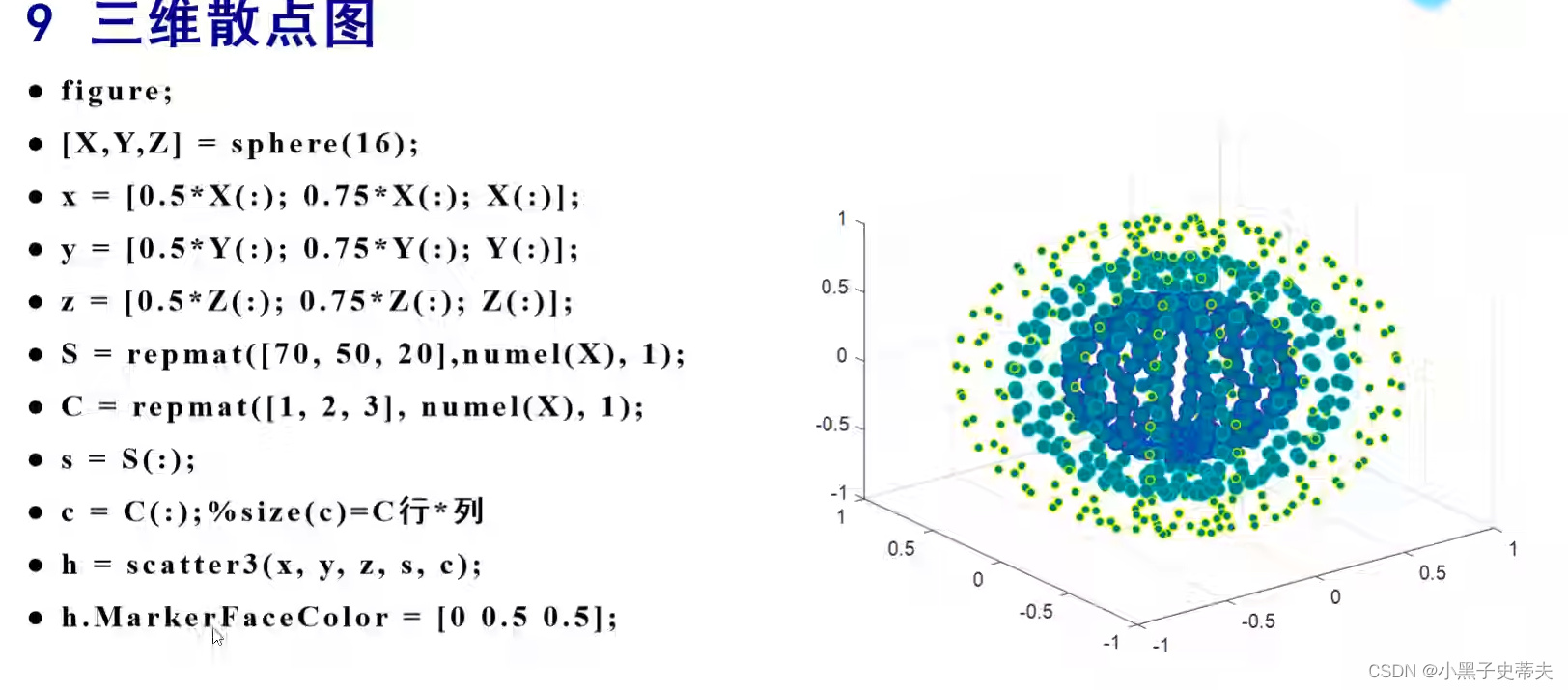
- 7.8 三维散点图
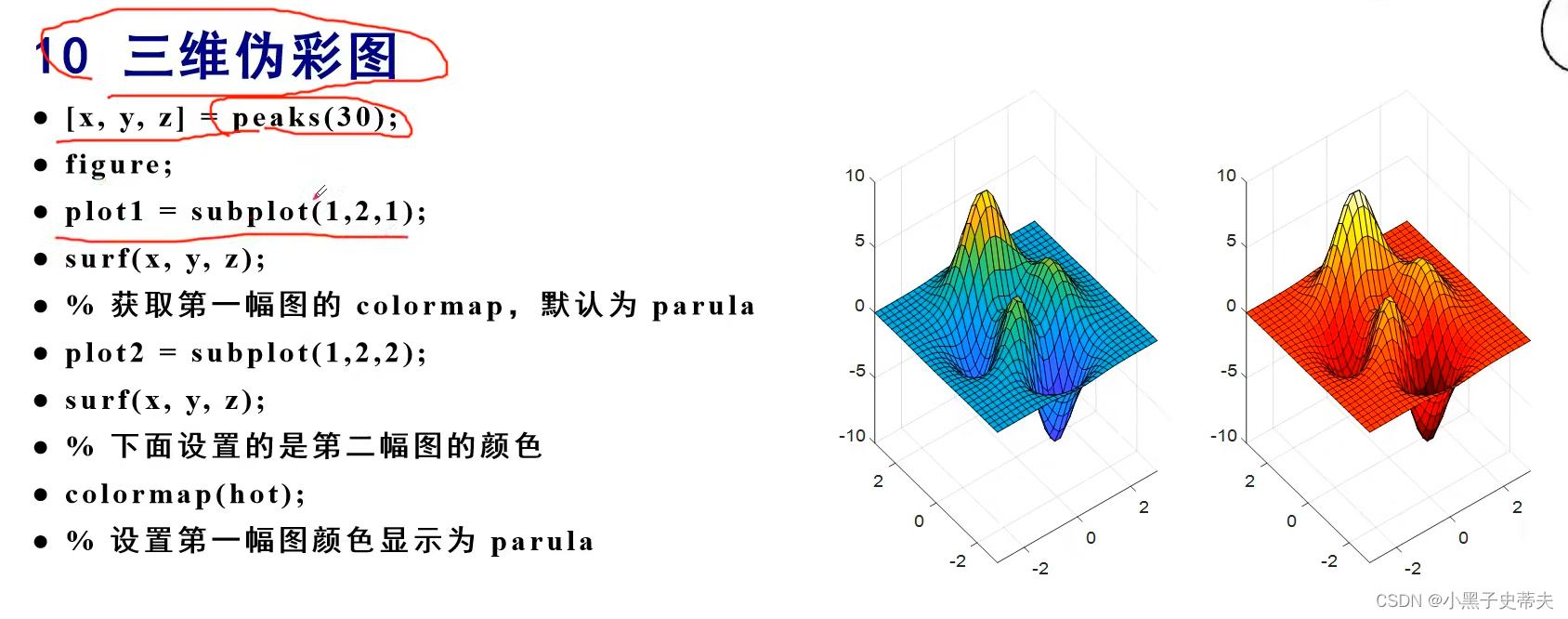
- 7.9 surf 与 colormap 三维伪彩图
- 7.10 shading interp 裁剪伪彩图
- 7.11 contour 等高线图
- 7.11.1 三维等高线图
- 7.11.2 等高线填充图
- 7.12 三维矢量场图
- 7.13 伪彩图+投影图
- 7.14 分子模型图
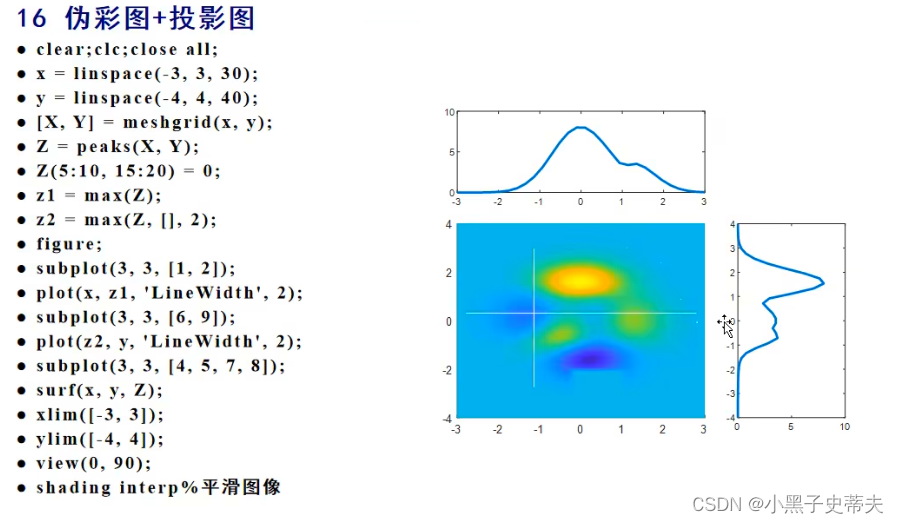
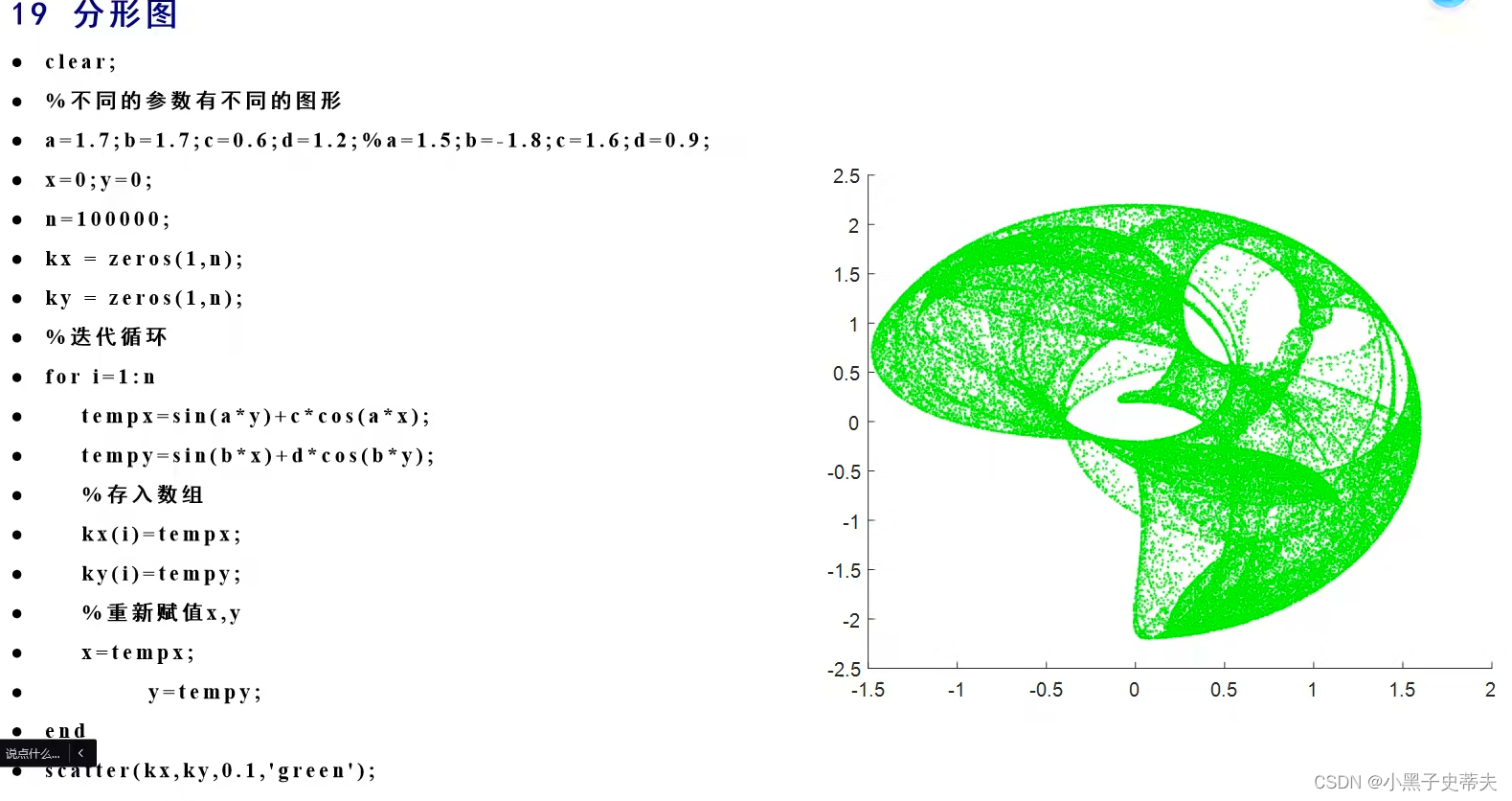
- 7.15 分形图
- 8. Matlab的数列与极限
- 8.1 sum 数组求和
- 8.2 nansum 和 cumsum累积和
- 8.3 cumtrapz计算累积梯形积分
- 8.4 prod 求数组元素乘积
- 8.5 其他计算乘积相关的函数
- 8.6 limit极限 与 diff导数
- 8.7 symsum 级数求和
- 8.8 等差、等比数列求和
- 8.9 int 计算定积分
- 8.10 integral2 计算二重积分
- 8.11 integral3 计算三重积分
- 8.12 taylor 泰勒展开
- 8.13 fourier 傅里叶变换
- 8.13.1 ffft 快速傅里叶变化
- 8.14 拉普拉斯变化
- 9. Matlab的微分方程
- 9.1 dsolve 求解微分方程
- 9.2 欧拉法
- 9.2.1 改进的欧拉法
- 9.3 ode龙格库塔法
- 9.4 偏微分方程
- 9.4.1 有限元法
- 9.4.2 求解区域的设置
- 9.4.3 求解区域的网格化
- 9.4.4 求解椭圆型PDE
- 9.4.5 pdetool辅助实现
- 10. matlab的线性规划
- 10.1 范数
- 10.2 序列
- 10.3 梯度
- 10.4 凸集和凸函数
- 10.5 凸规划
- 10.6 线性规划的标准
- 10.7 例题
1. Matlab界面与基本操作
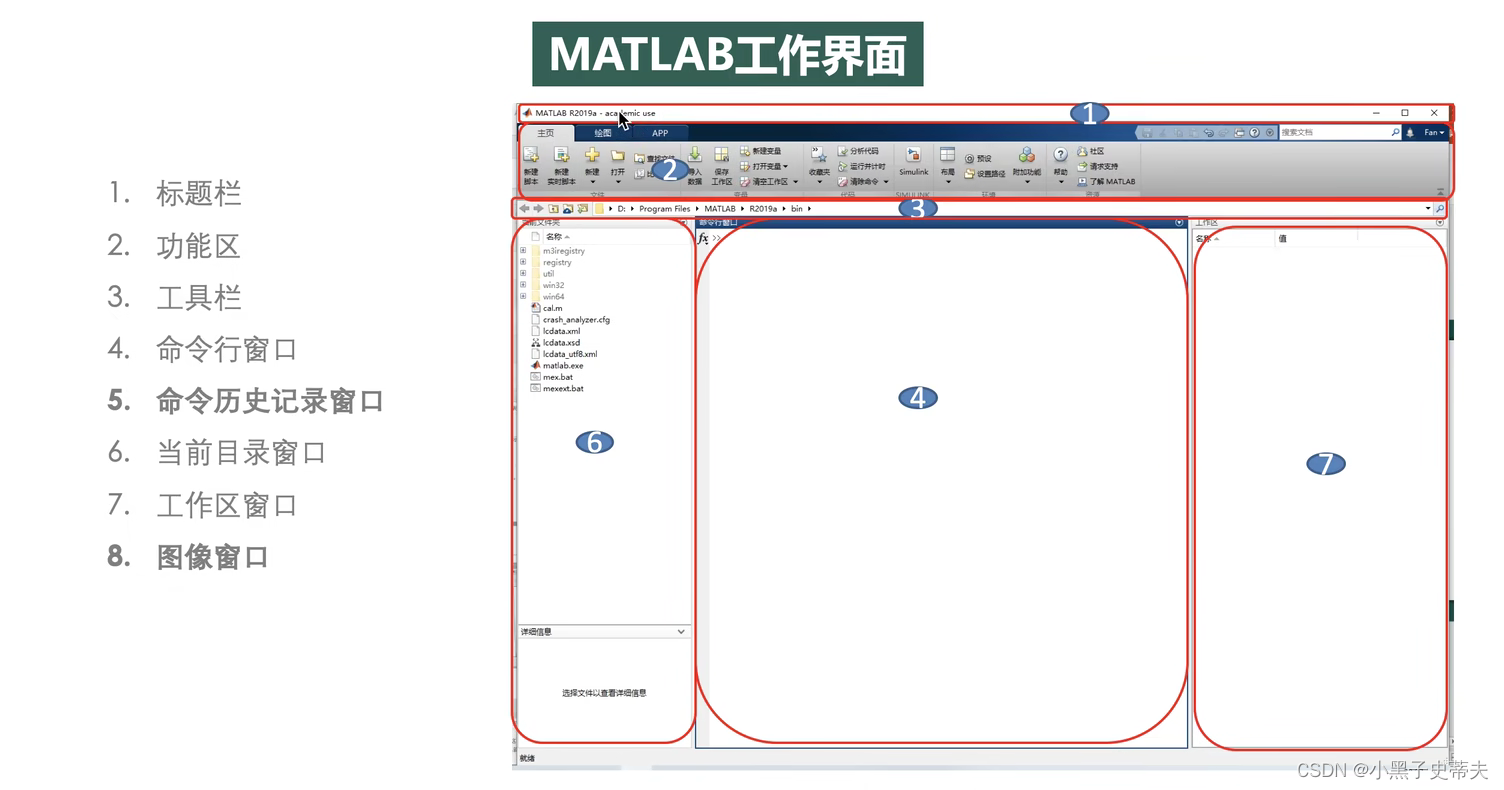
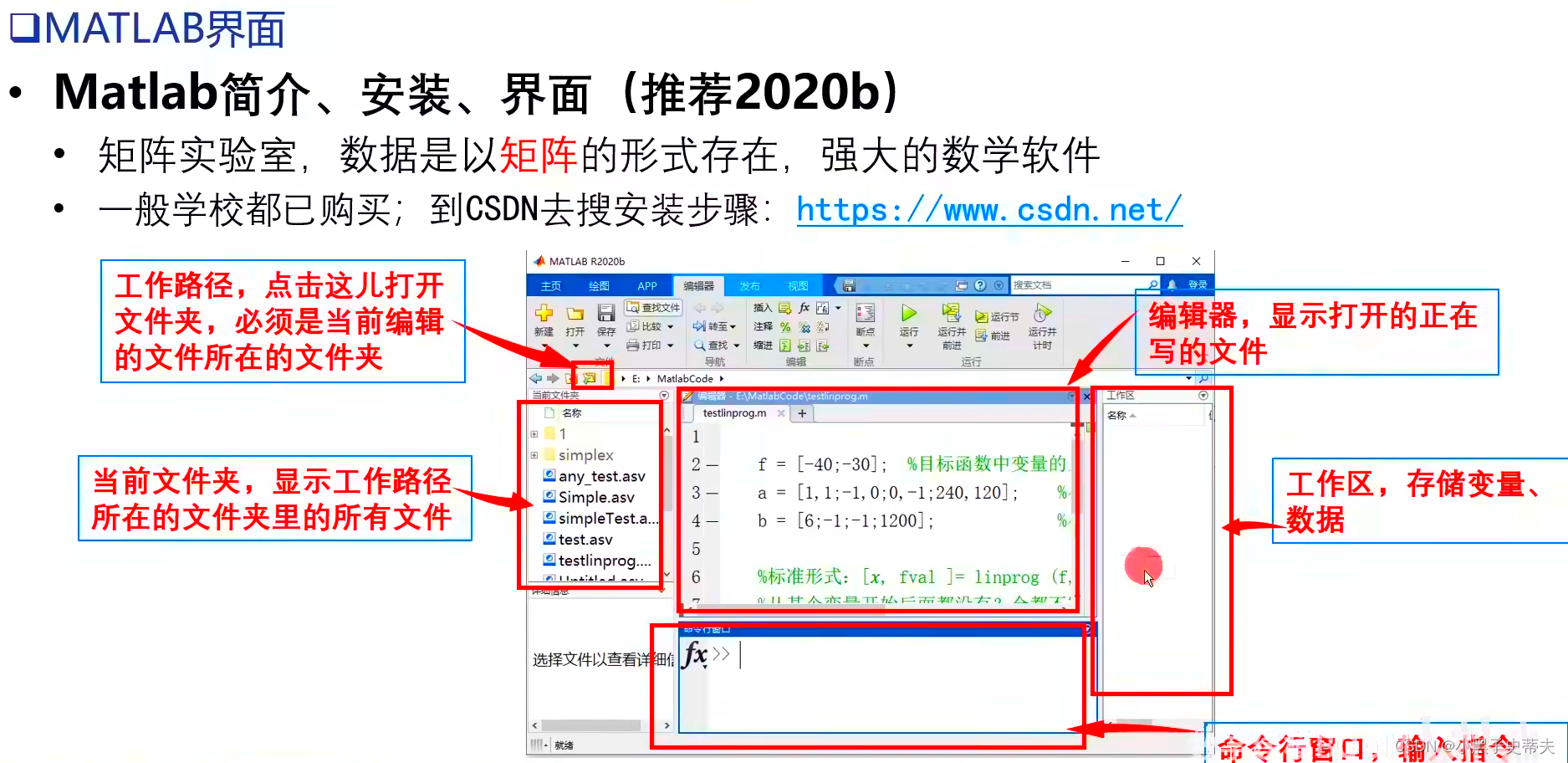
-
在
命令行输入指令- 输入完指令后,敲回车就执行
-
在
脚本文件中编写程序后运行- 脚本文件,就是存放代码的文件,尾缀.m
实时脚本文件界面更加方便,把结果实时显示在代码旁边,推荐使用。
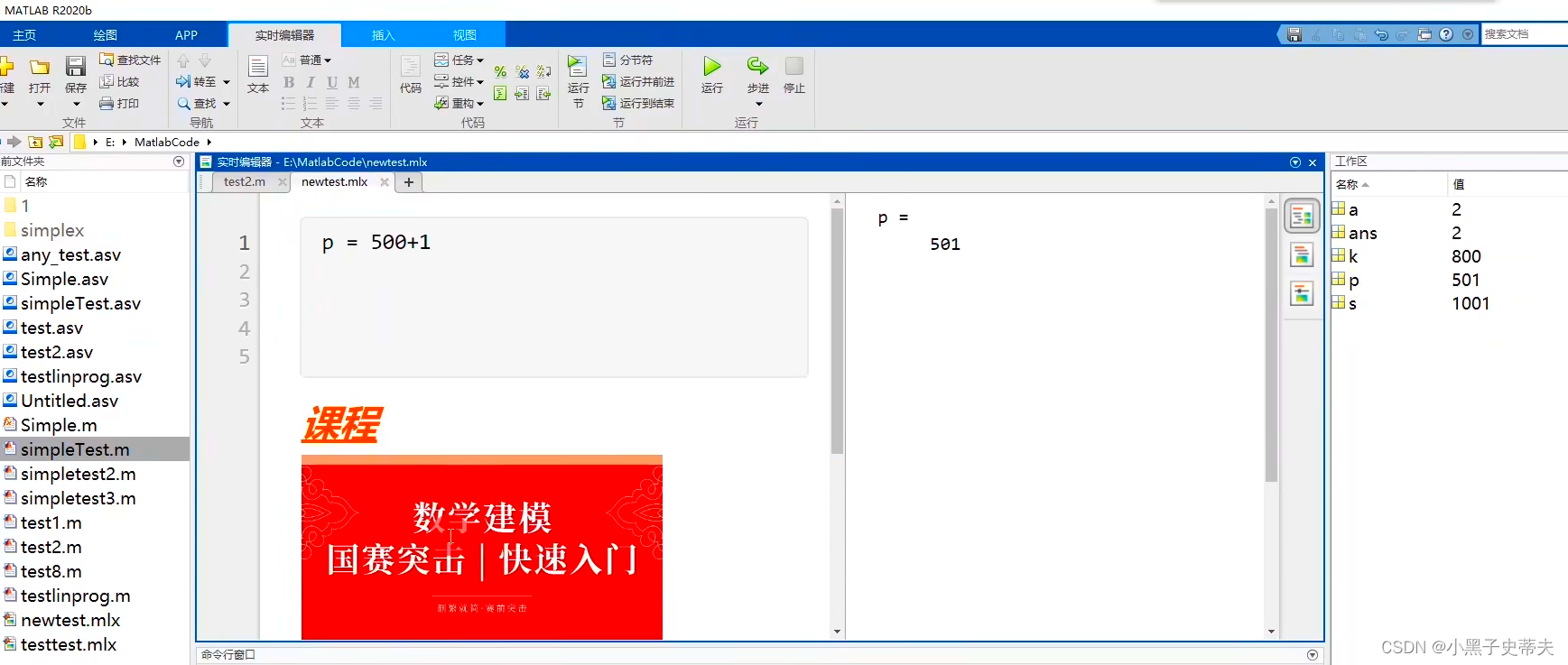
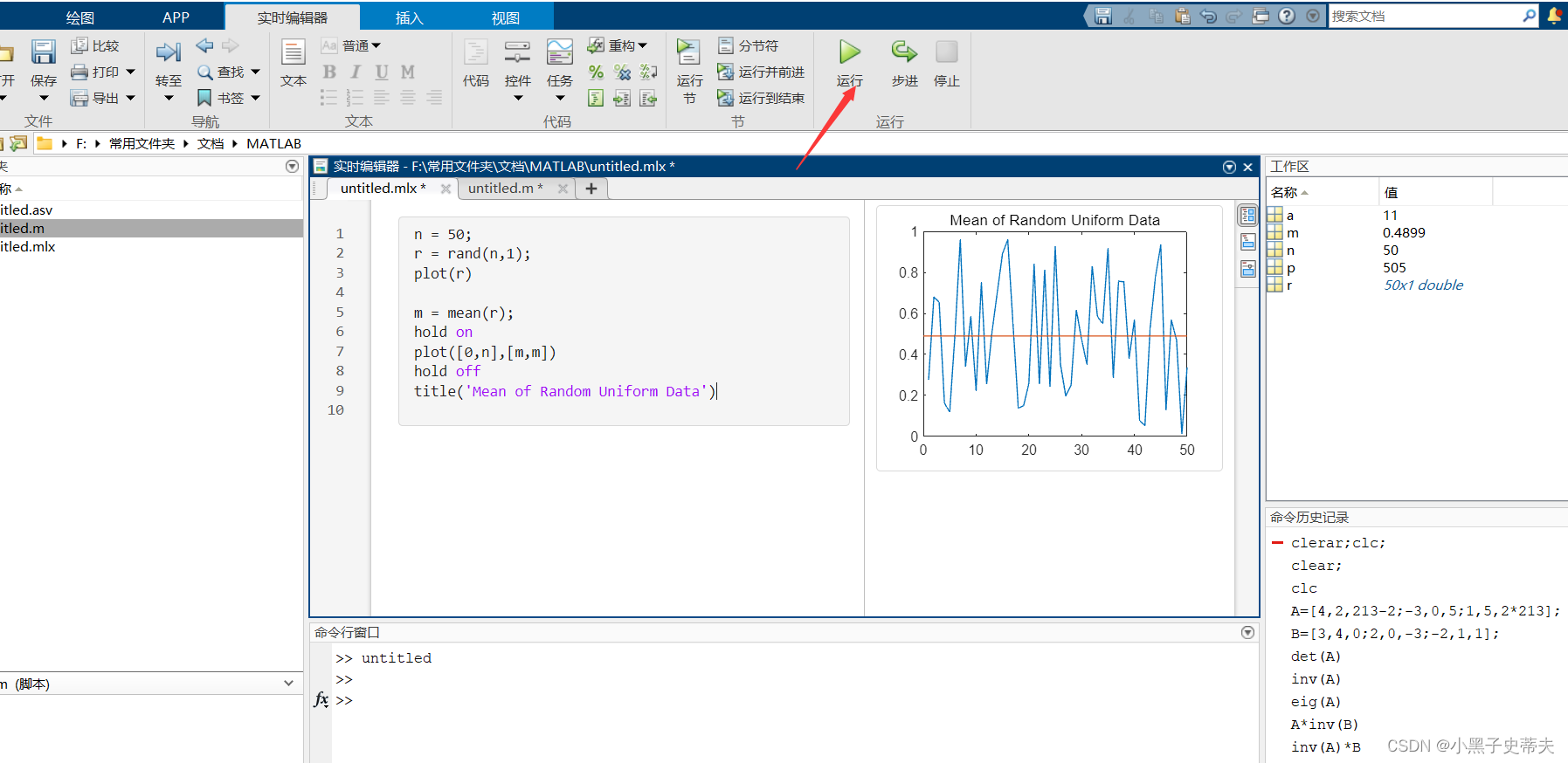
-
在函数文件中编写程序,然后在脚本文件中调用
- 函数文件相当于做好一个工具,以后用到的时候直接调用,尾缀也是
.m - 有固定格式,例如:
function [sigma, theta,x, y, final_res] = Simple(f,a, b. index)
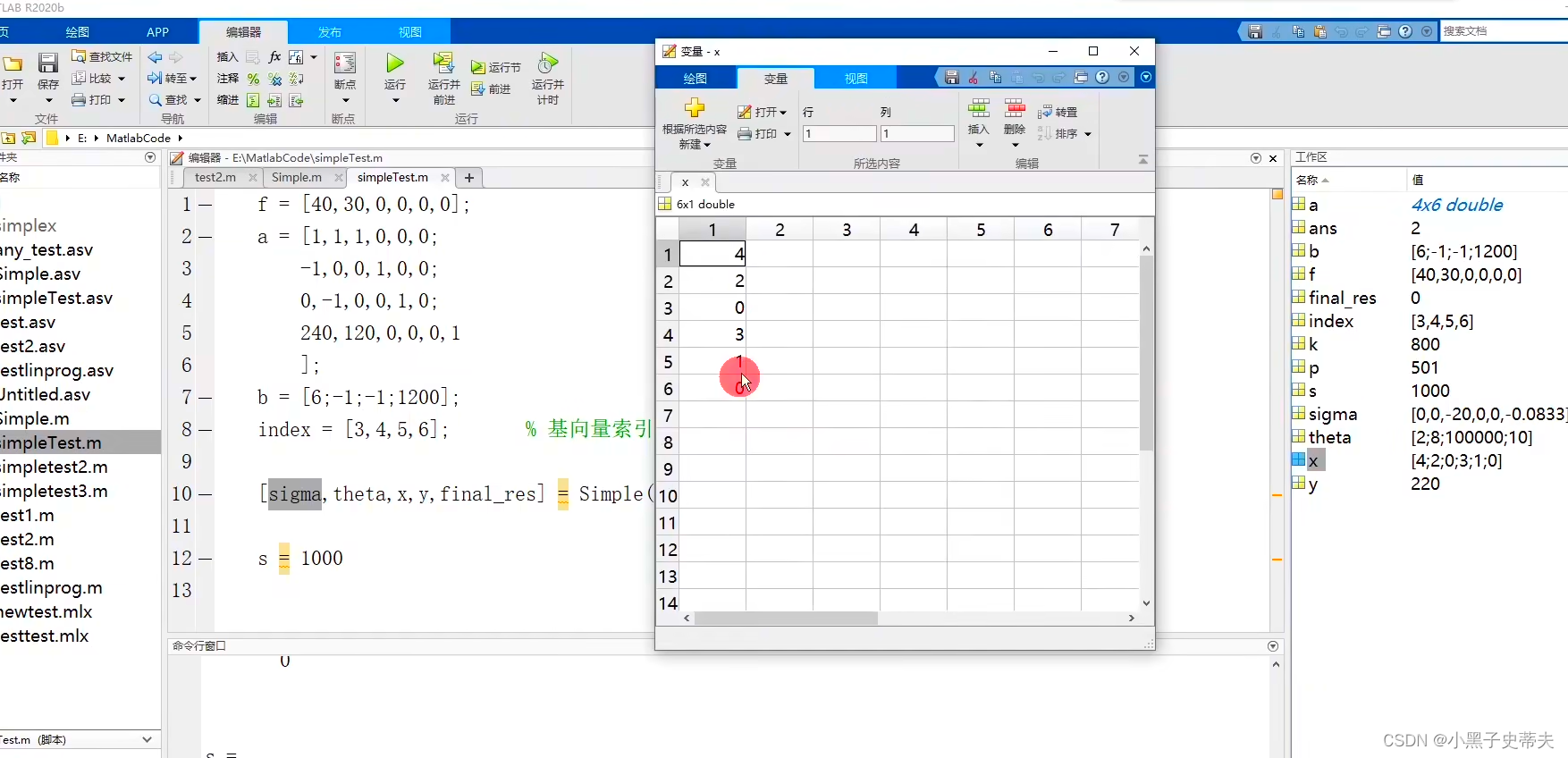
- 函数文件相当于做好一个工具,以后用到的时候直接调用,尾缀也是
-
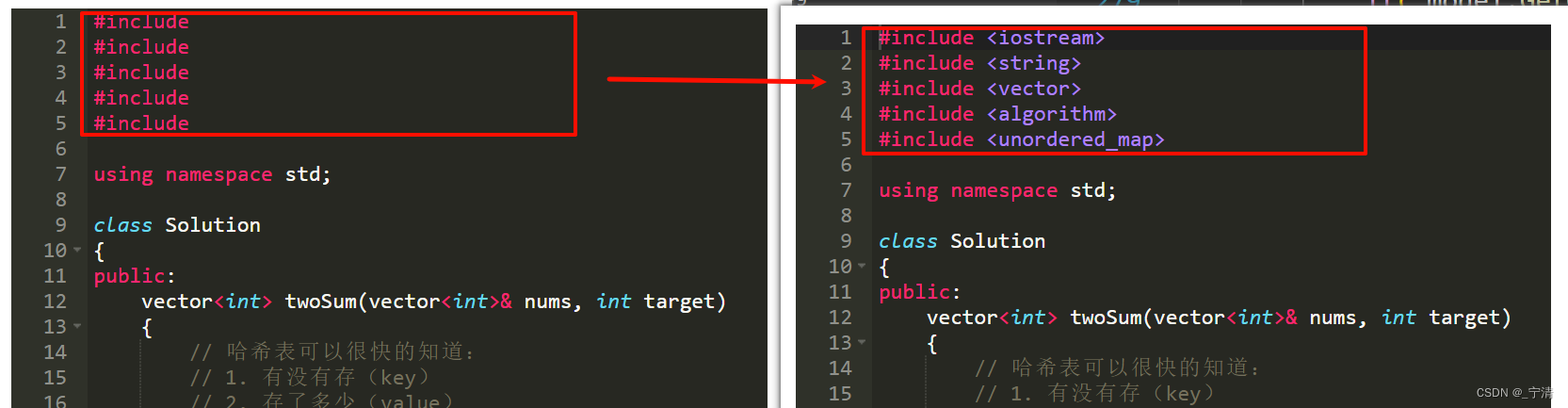
符号
- 注释:
%后面写的内容都是注释 - 分号:写完一行代码,该行末尾加个分号
;,会执行计算,但不在命令行窗口中显示输出 - 命令行输入:
clc(清空命令行),clear(清空工作区),按上方向键调用历史命令(很方便)
- 注释:
-
实时脚本文件
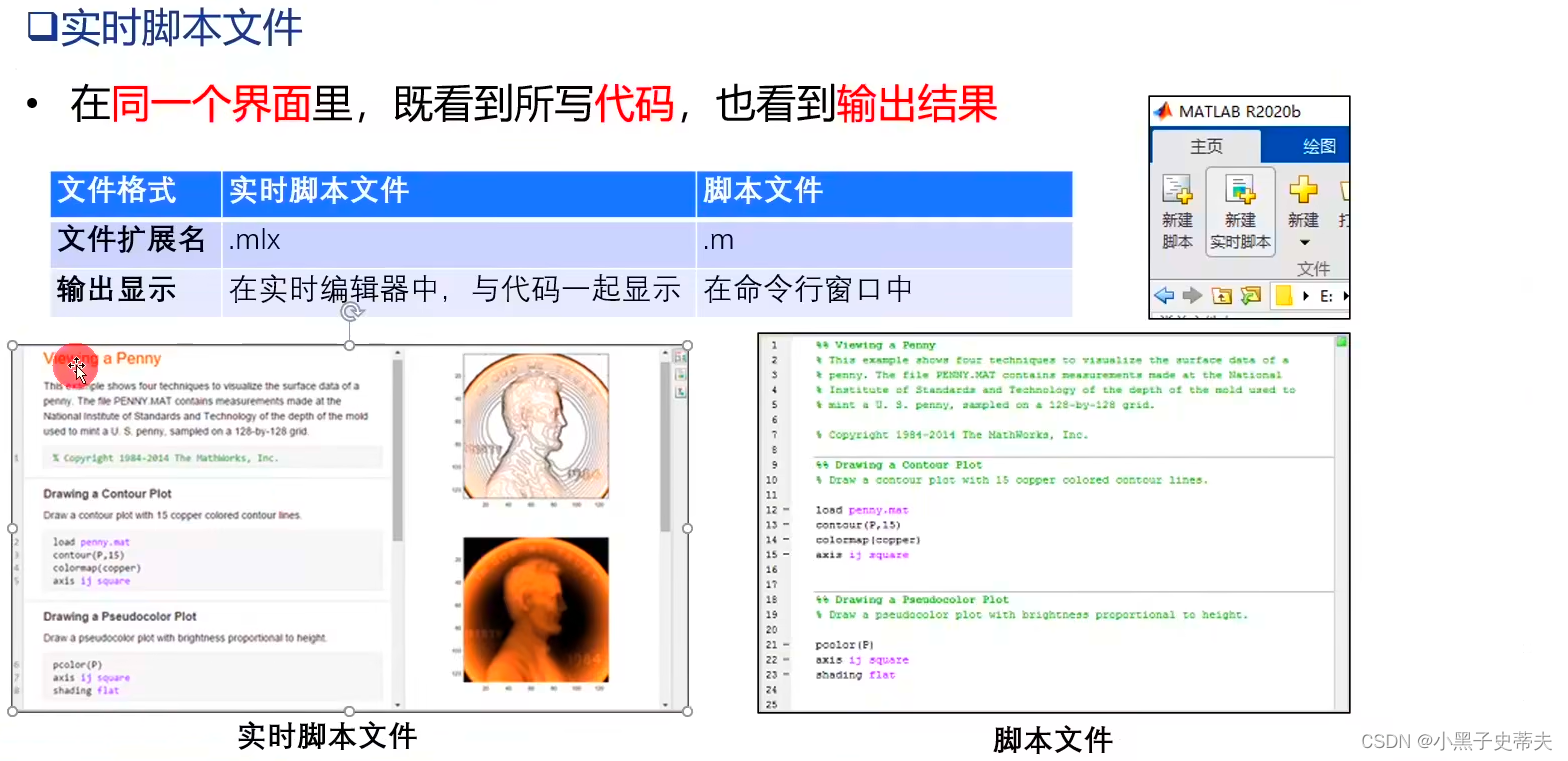
1.1 matlab帮助系统

-
help linspace函数

-
who

-
whos

-
exist 变量 (变量检验)

-
what 查找文件位置
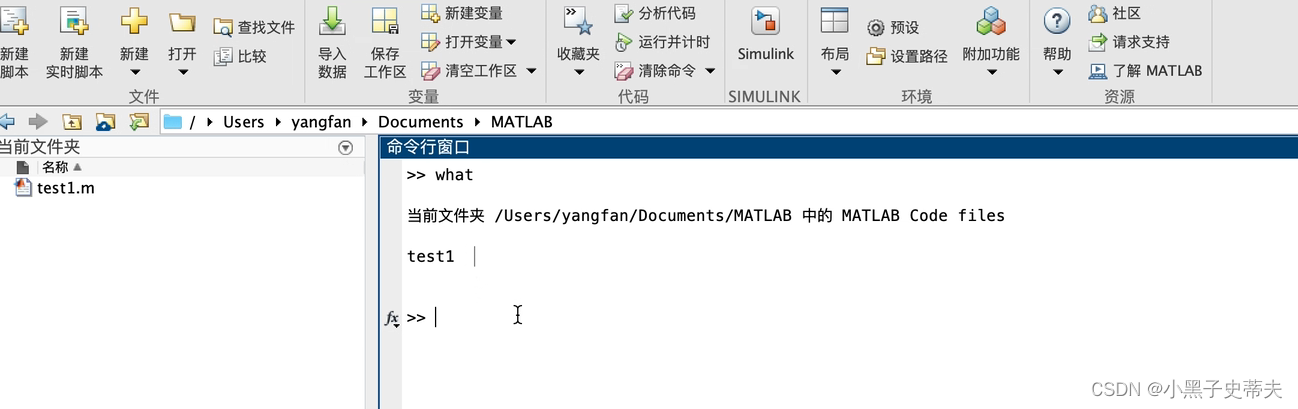
-
确定文件位置
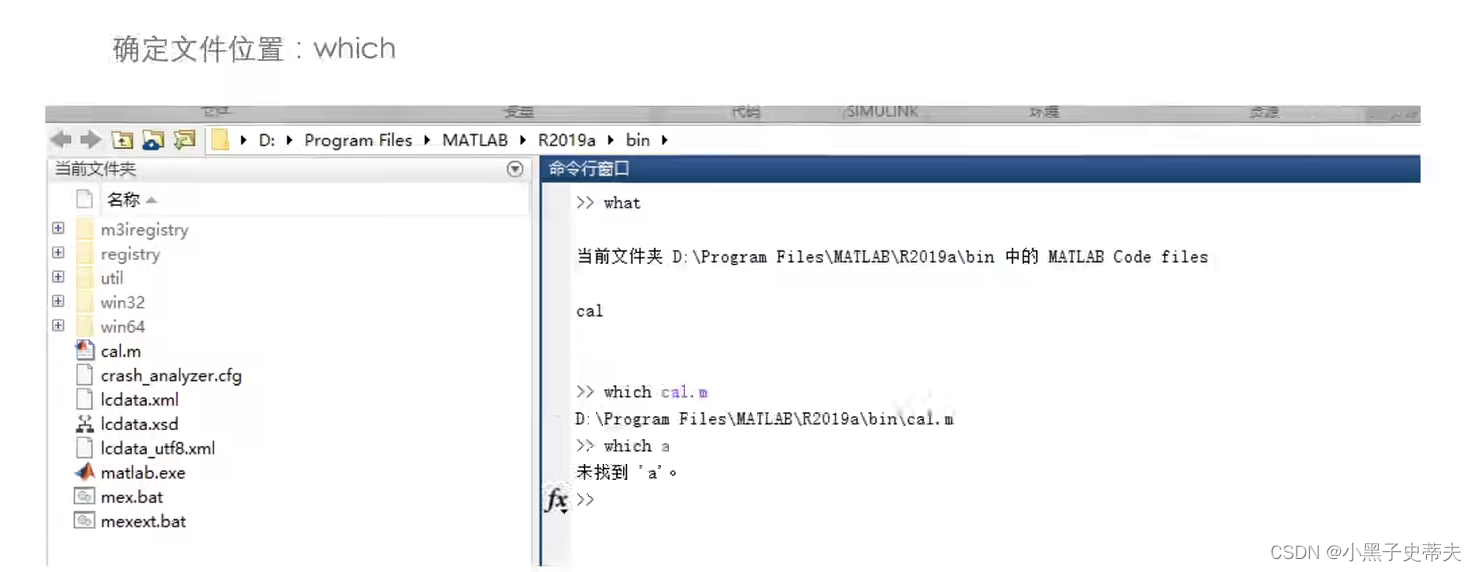
-
查看路径
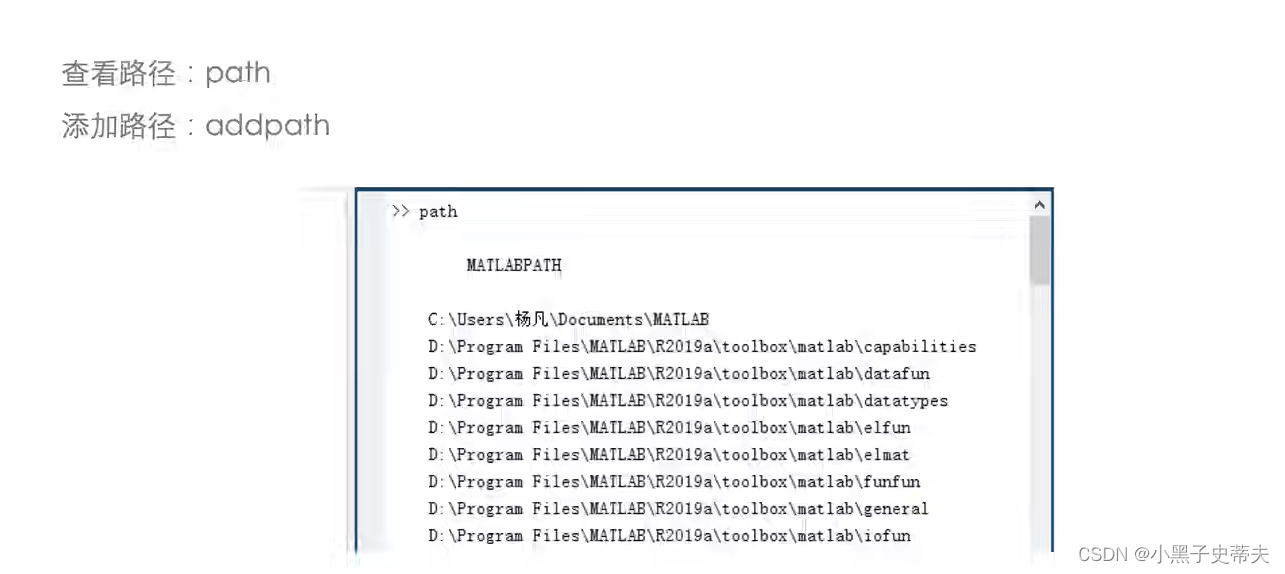
1.2 matlab命令



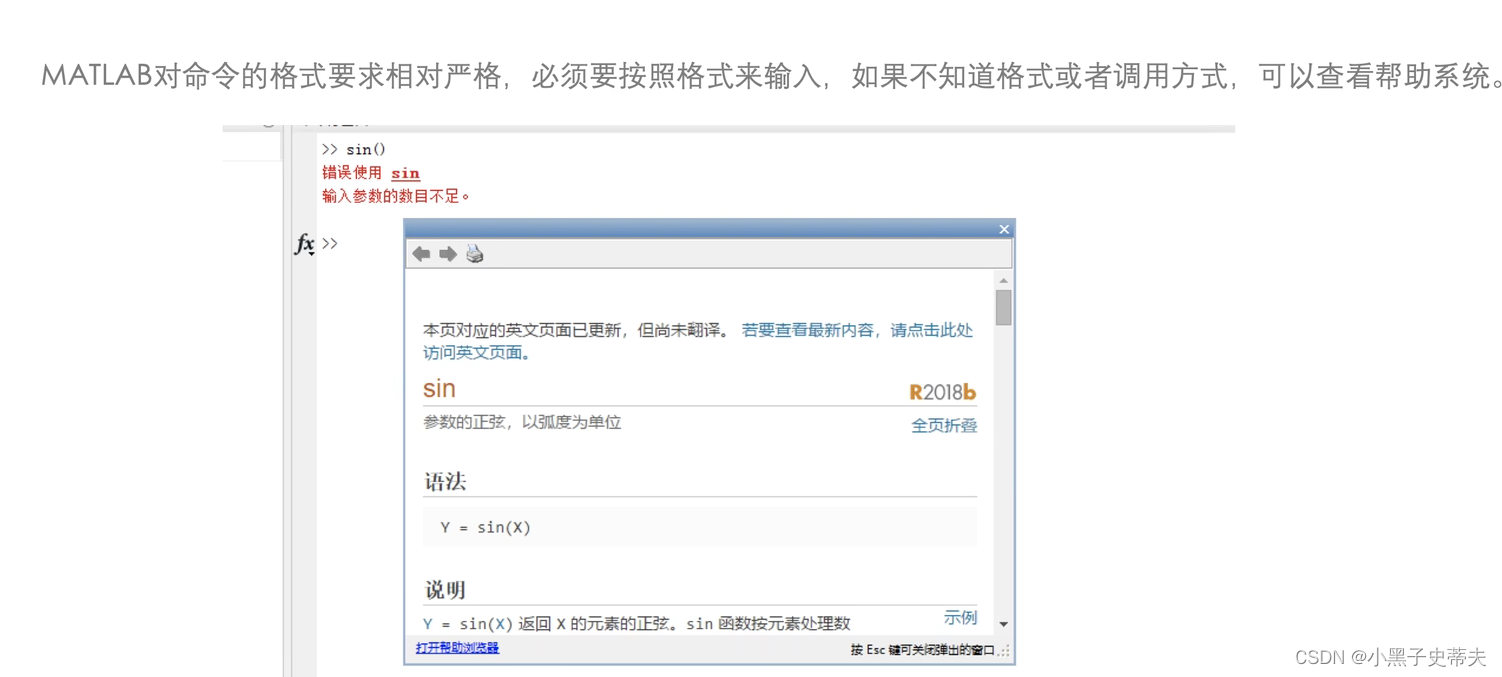

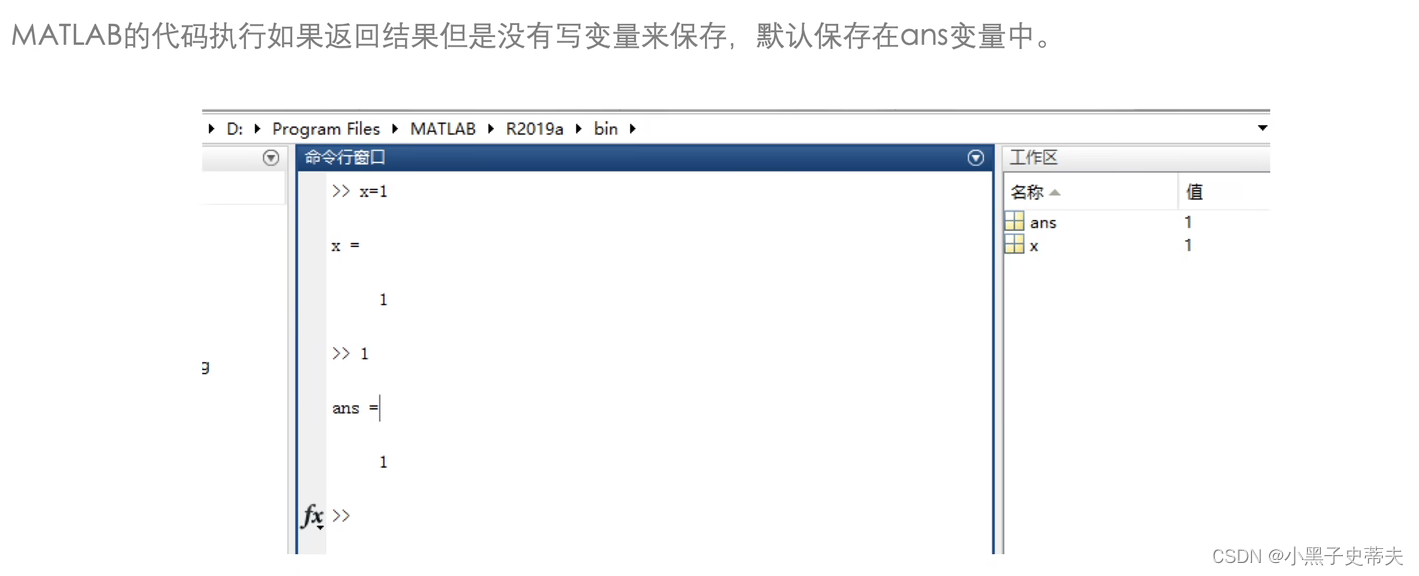
1.3 matlab功能符号
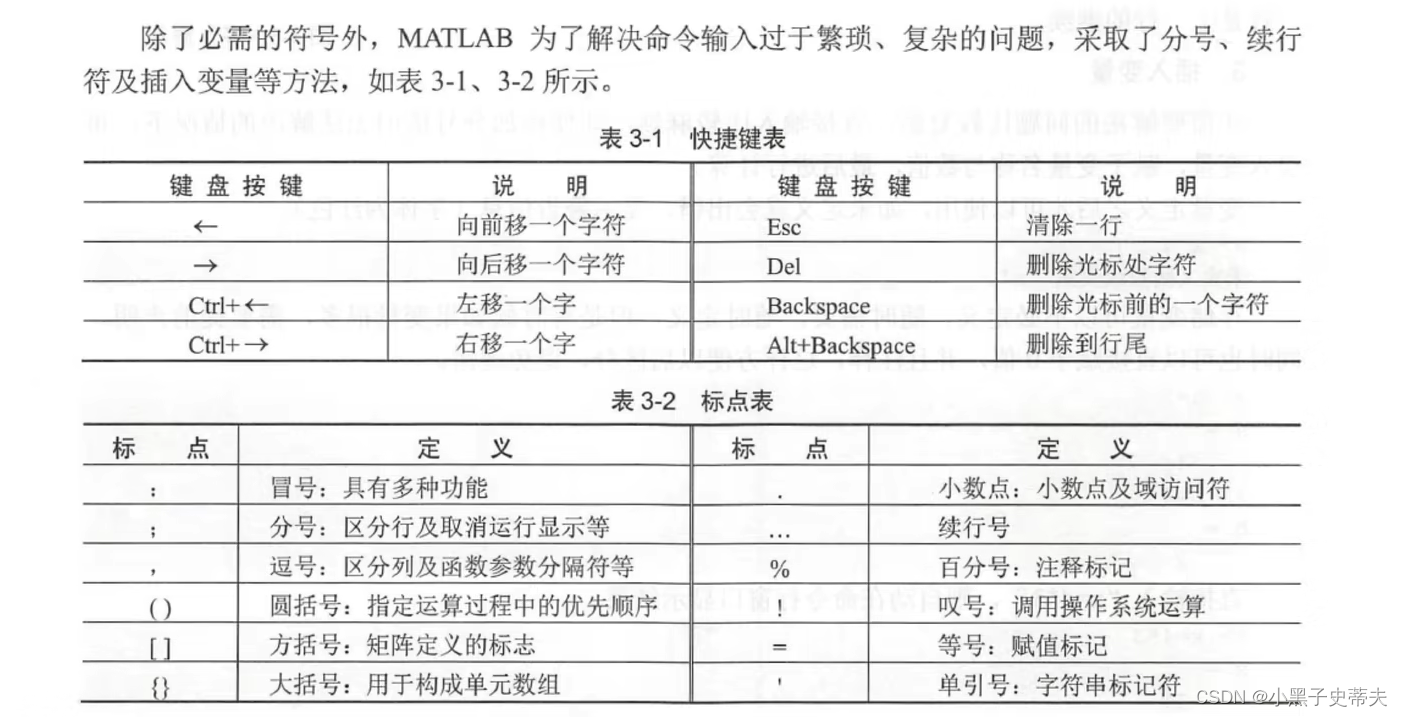

- 就是换行
...

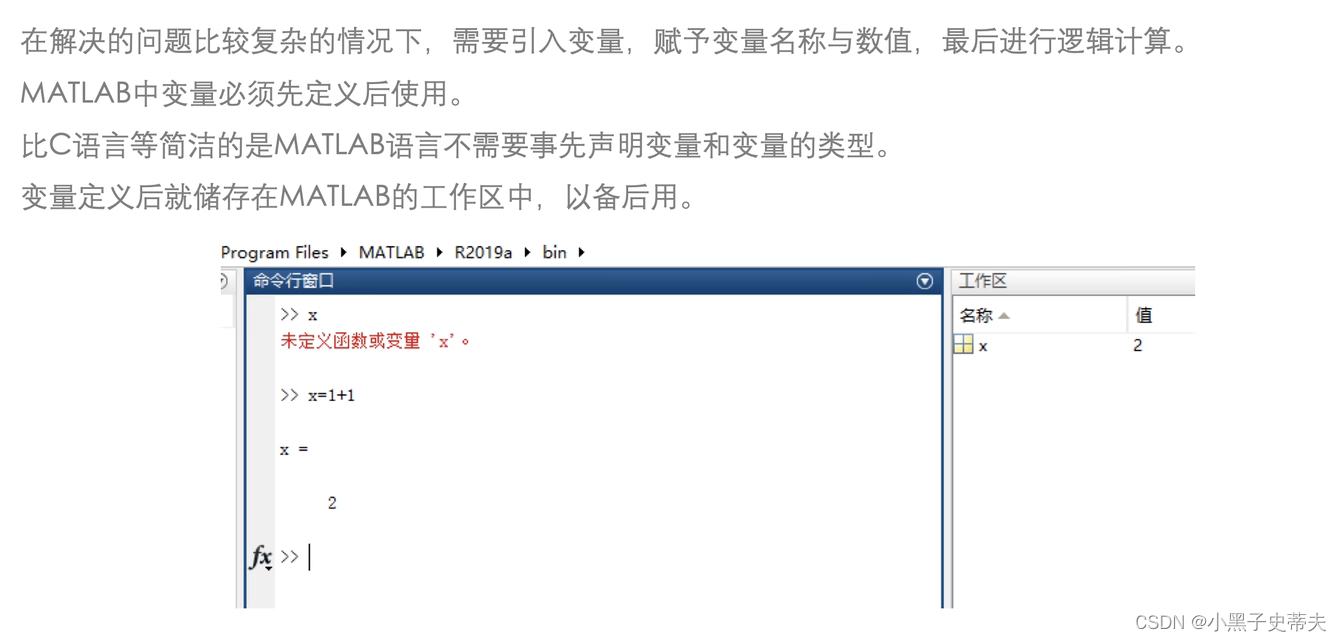
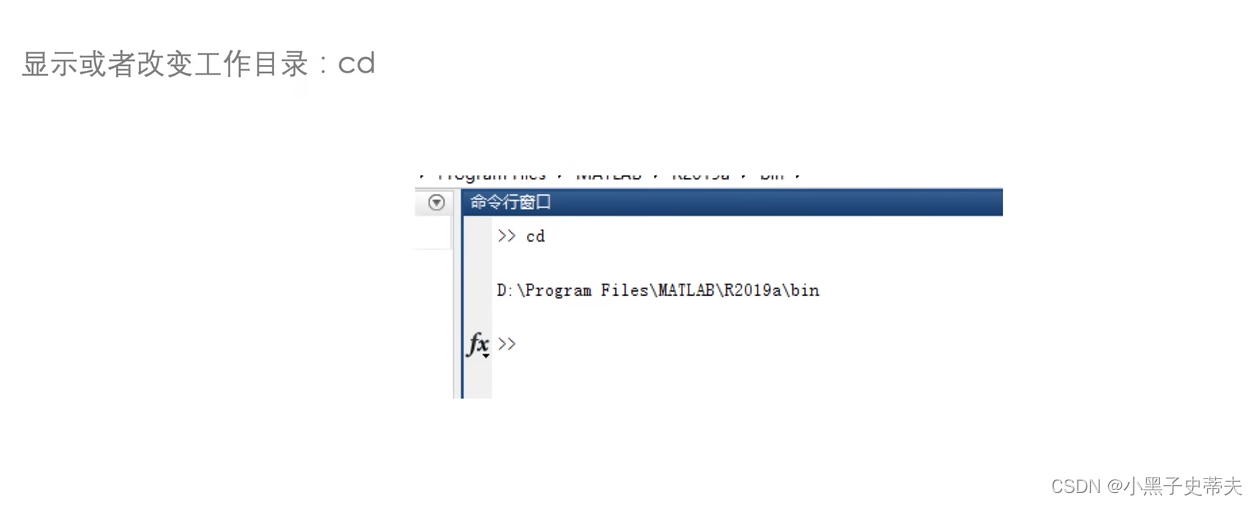
- 清除命令clc

- 清楚内存clear
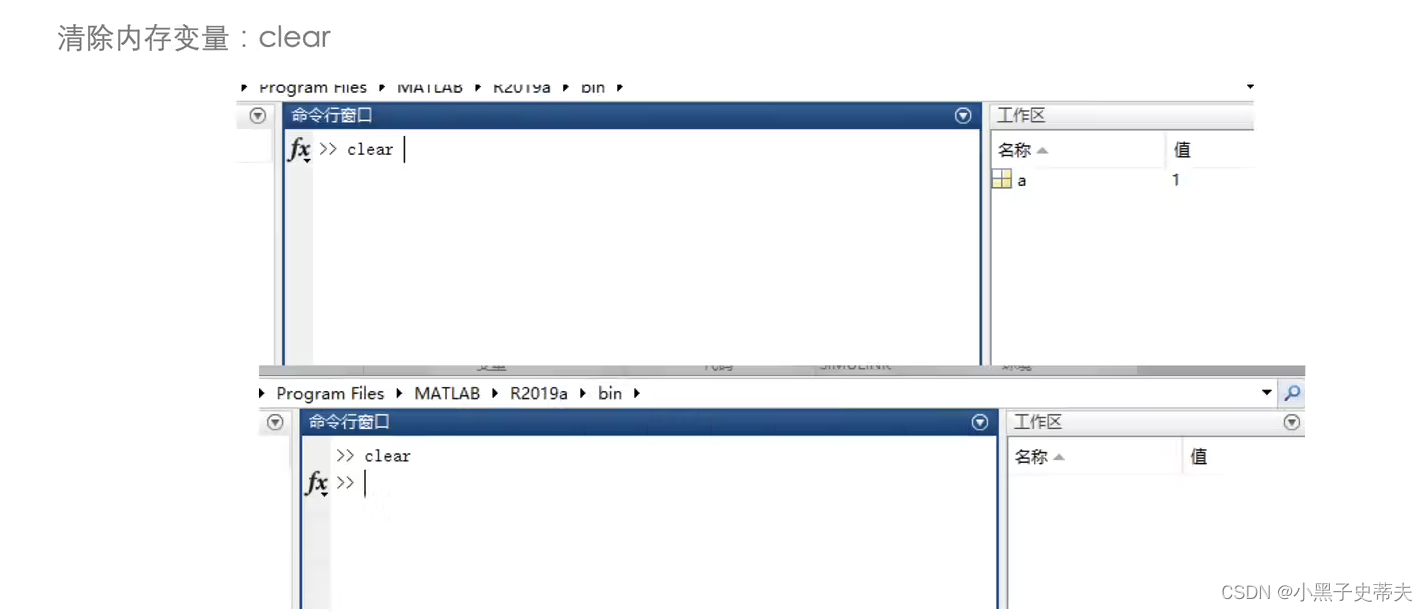
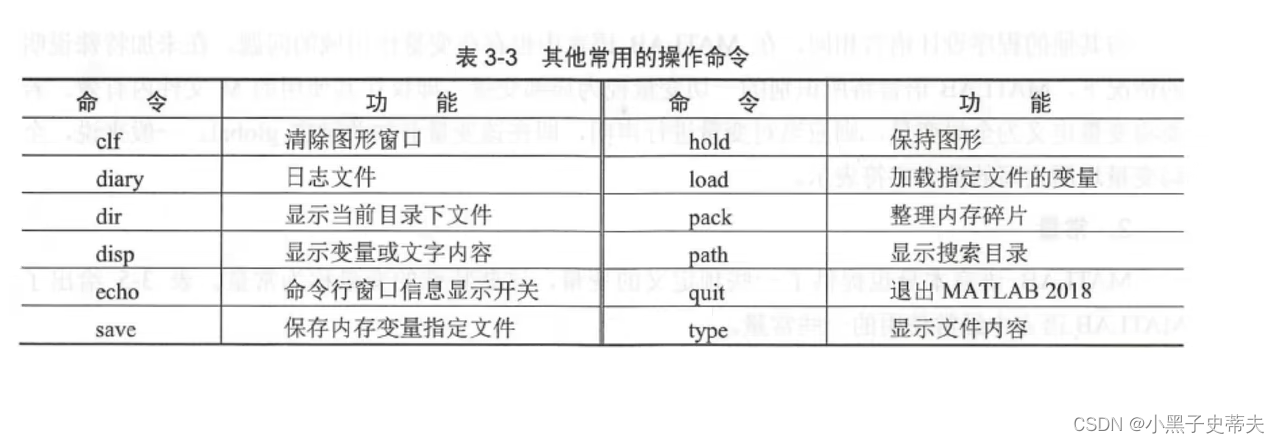
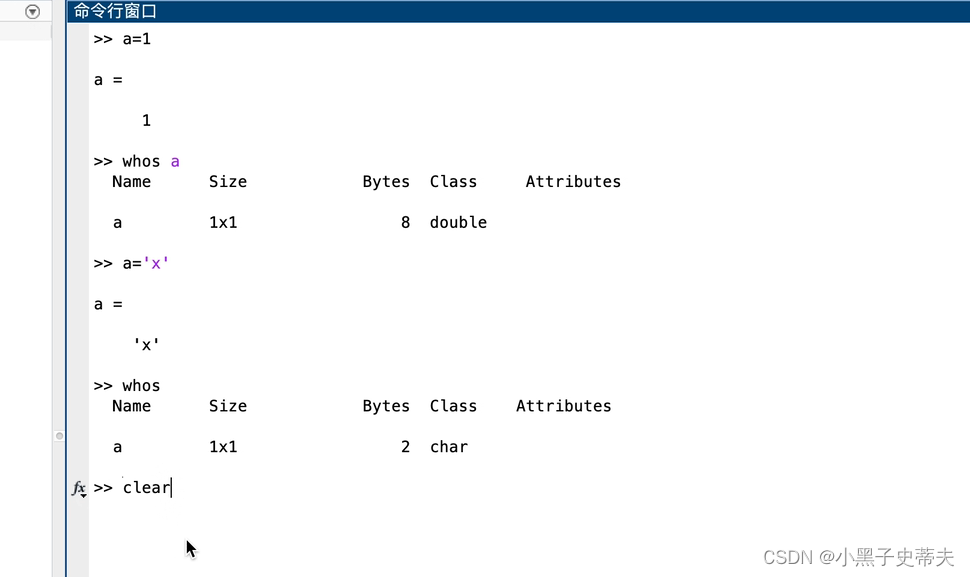
1.4 matlab的数据类型


例:
- matalb中的常量
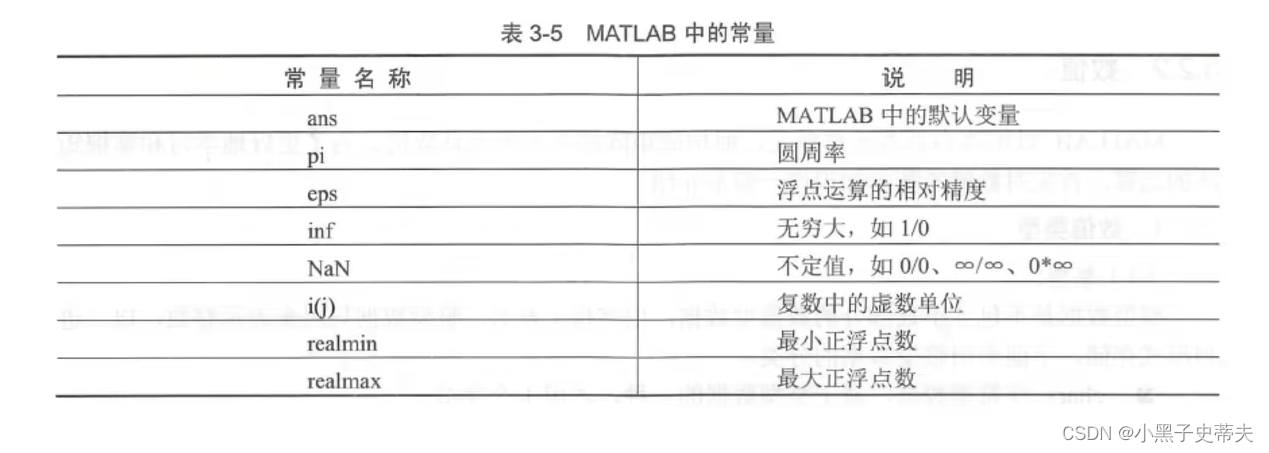
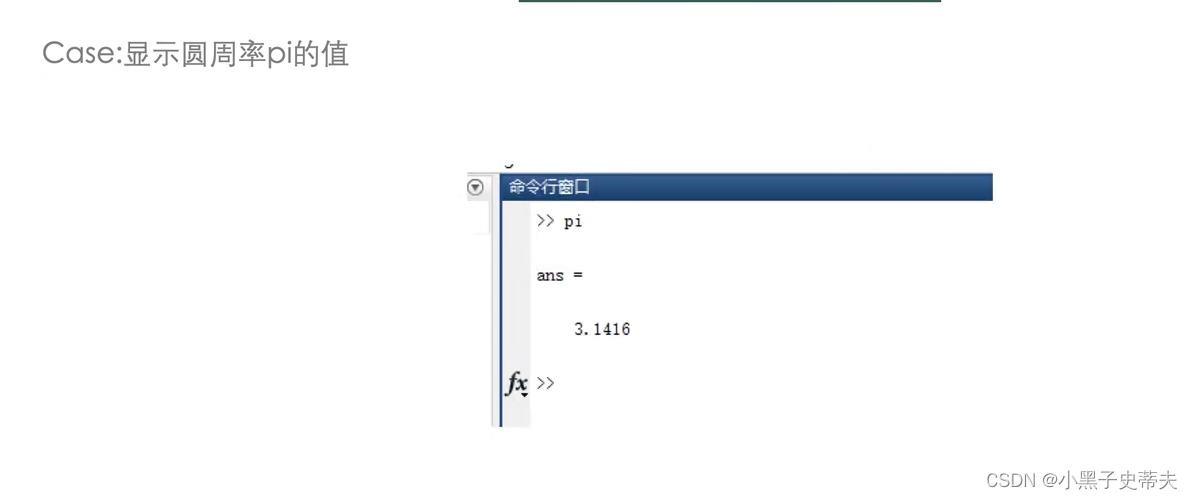


-
整型

-
浮点型



-
复数


1.5 函数计算

- 复数

1.6 matlab向量
-
直接输入法
[]

-
冒号法
:


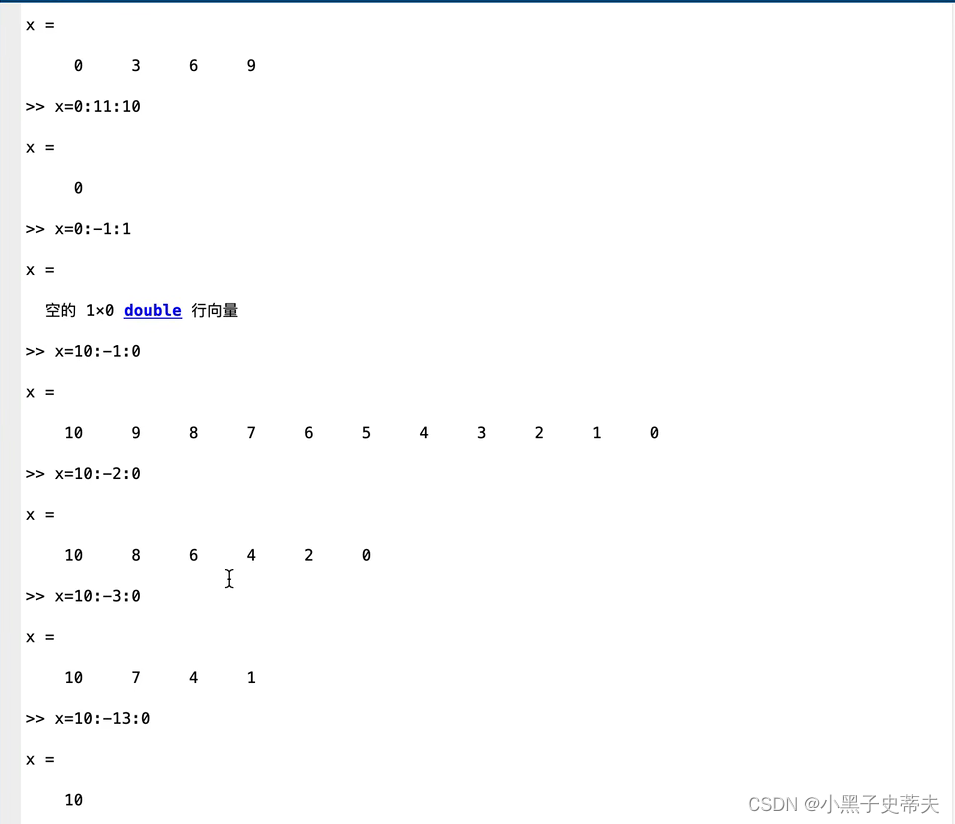
-
利用
linspace创建向量
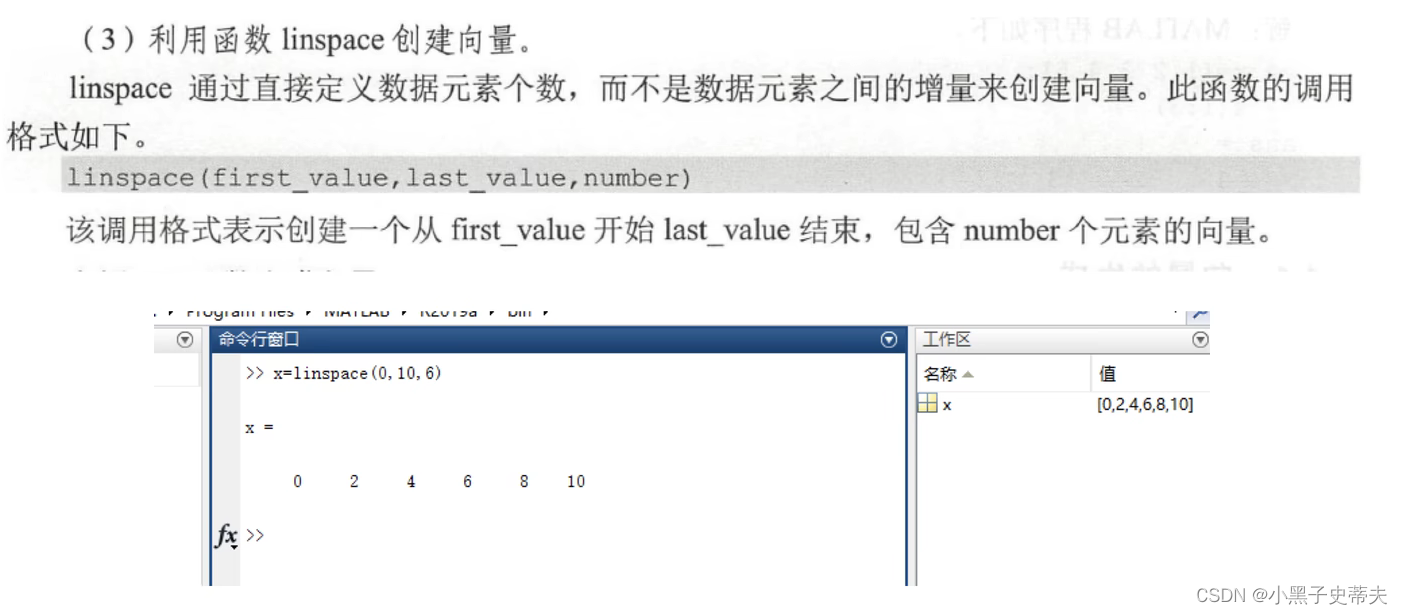
-
用
logspace创建一个对数分隔的向量

-
向量的引用:类似索引值

行向量变列向量加':例子x,x’ -
向量的点积运算

矩阵相乘的话,要求维度必须一致

-
向量的叉积运算

1.7 matlab多项式



多项式的除法运算:

1.8 M文件
1.9 函数文件
注意:函数文件的命名要同函数命名一致

1.10 matlab的程序结构

1.11 echo、warning和error函数

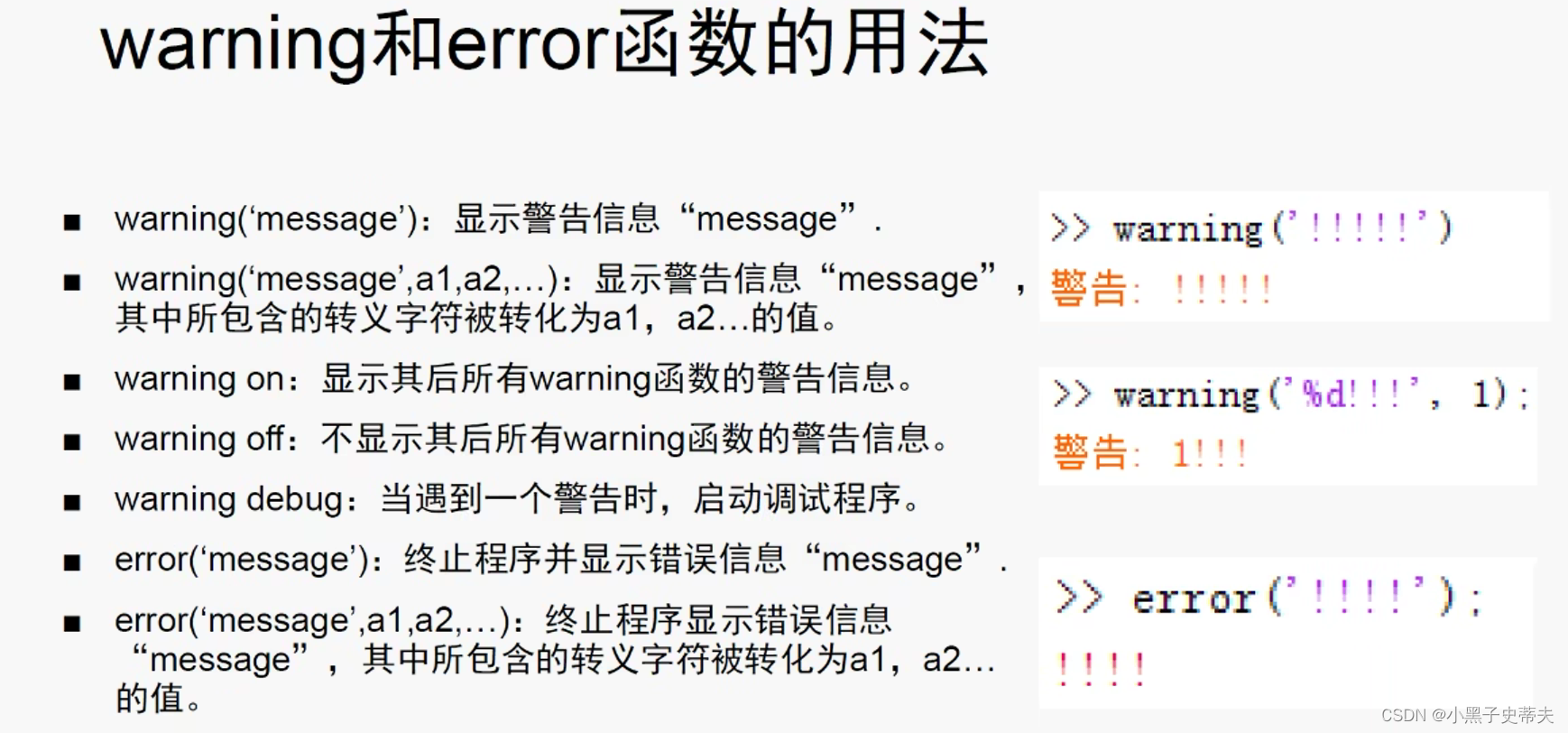
1.12 交互输入

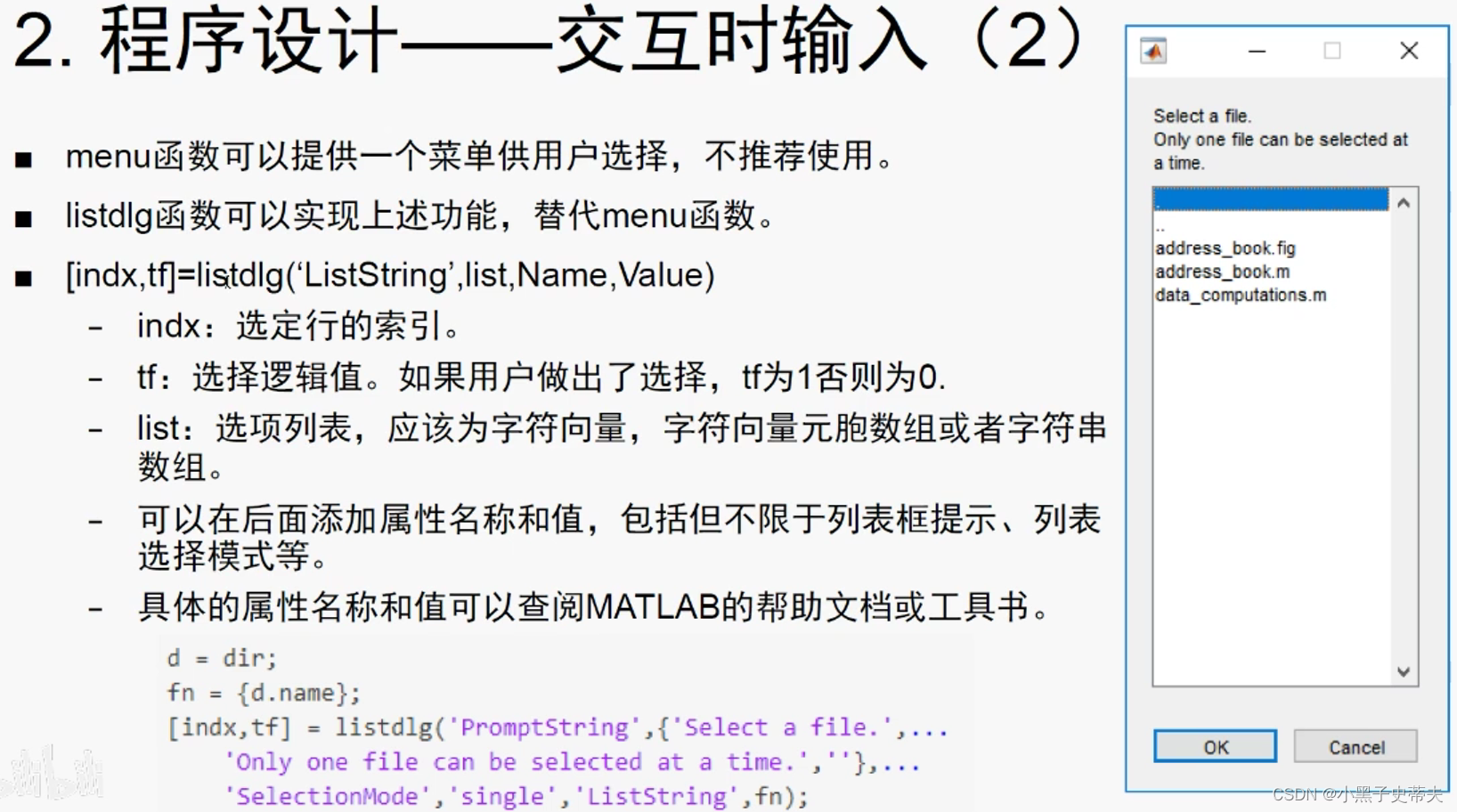
1.13 程序调试

1.14 设置断点调试
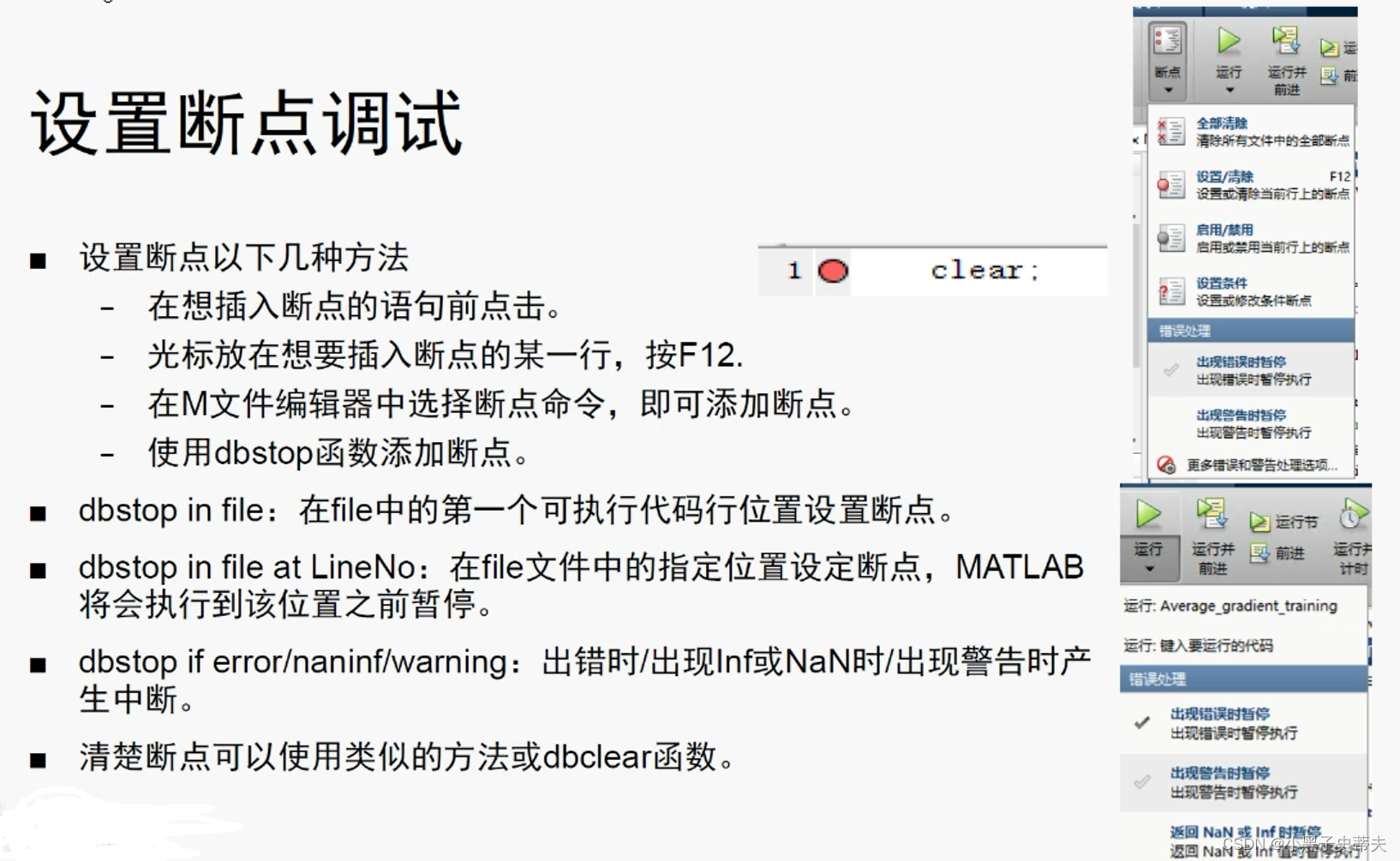
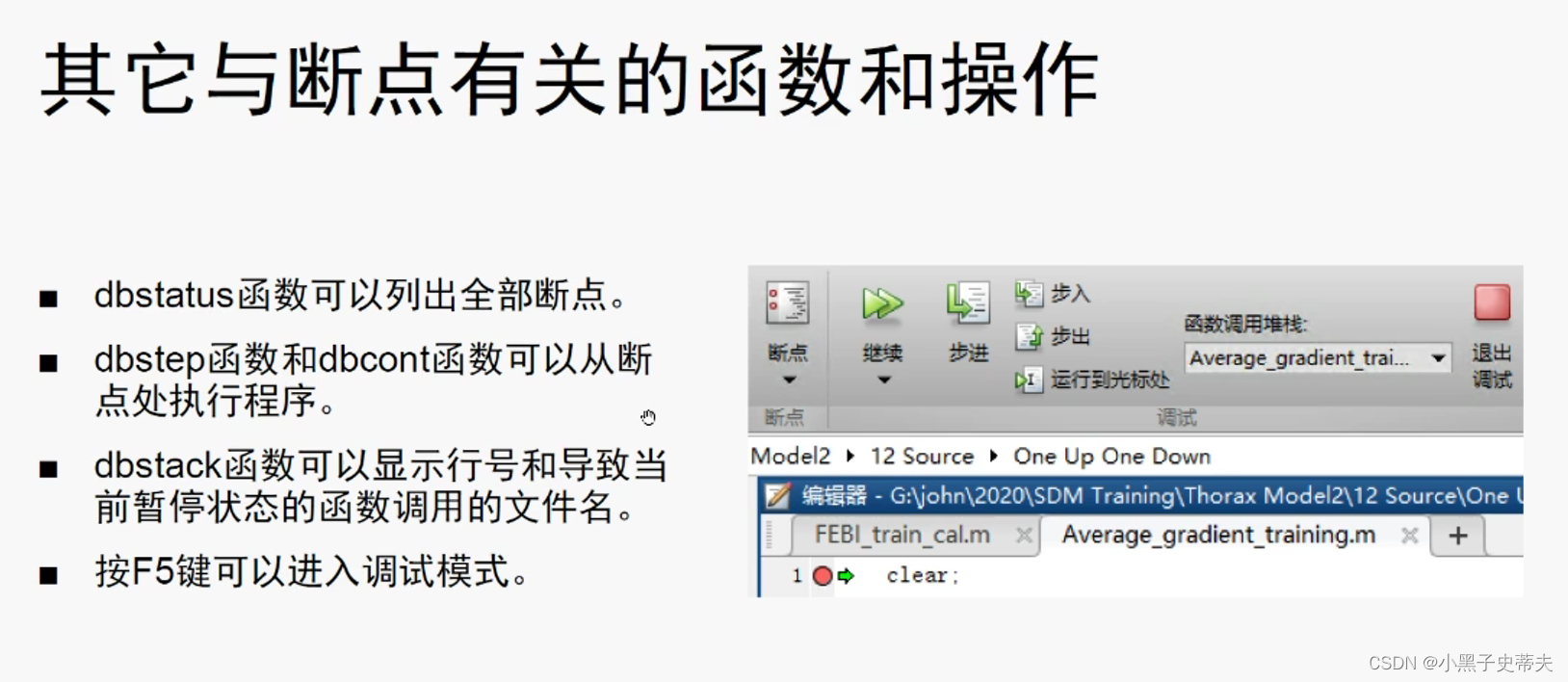
1.15 函数句柄 @
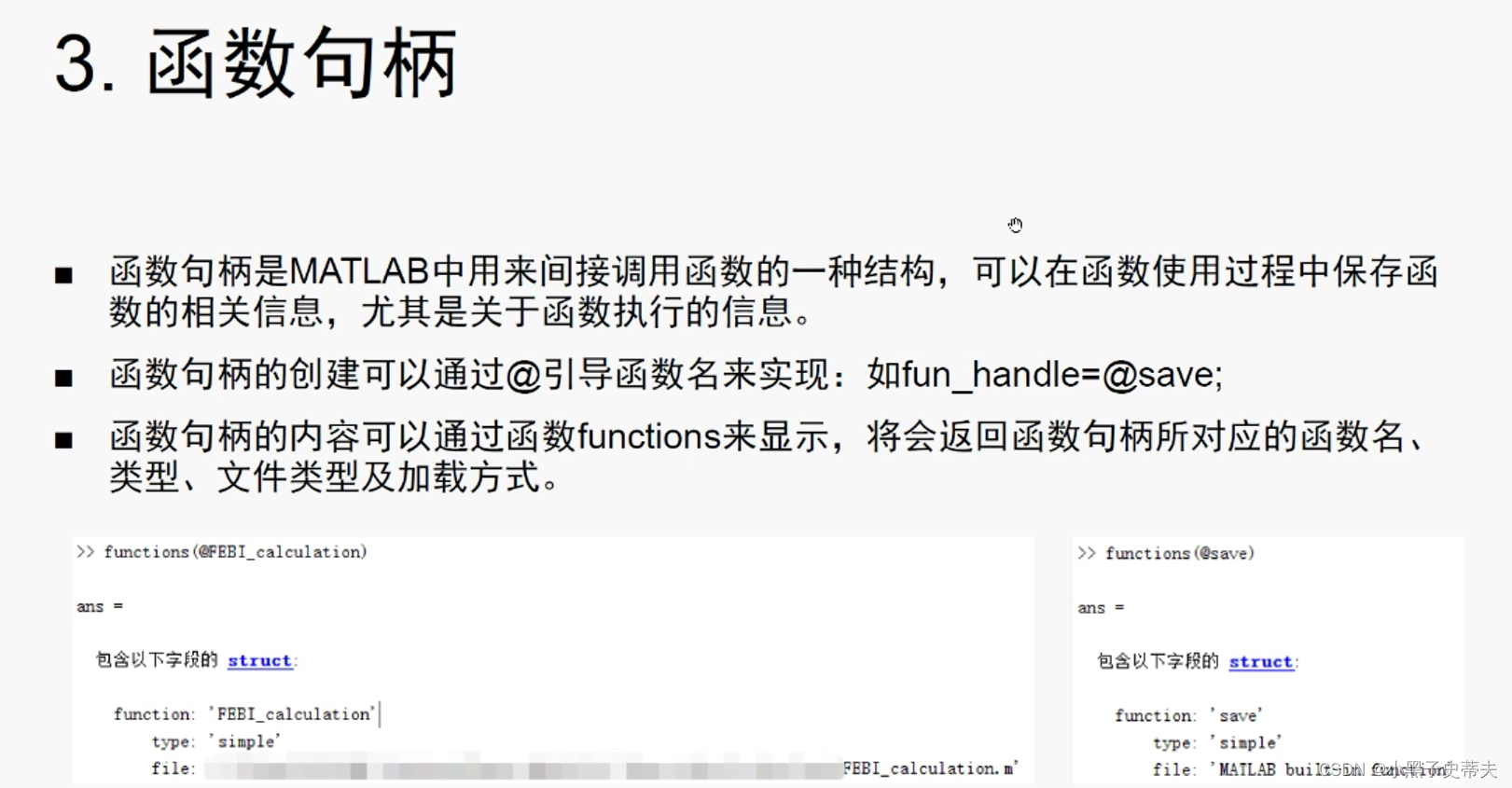
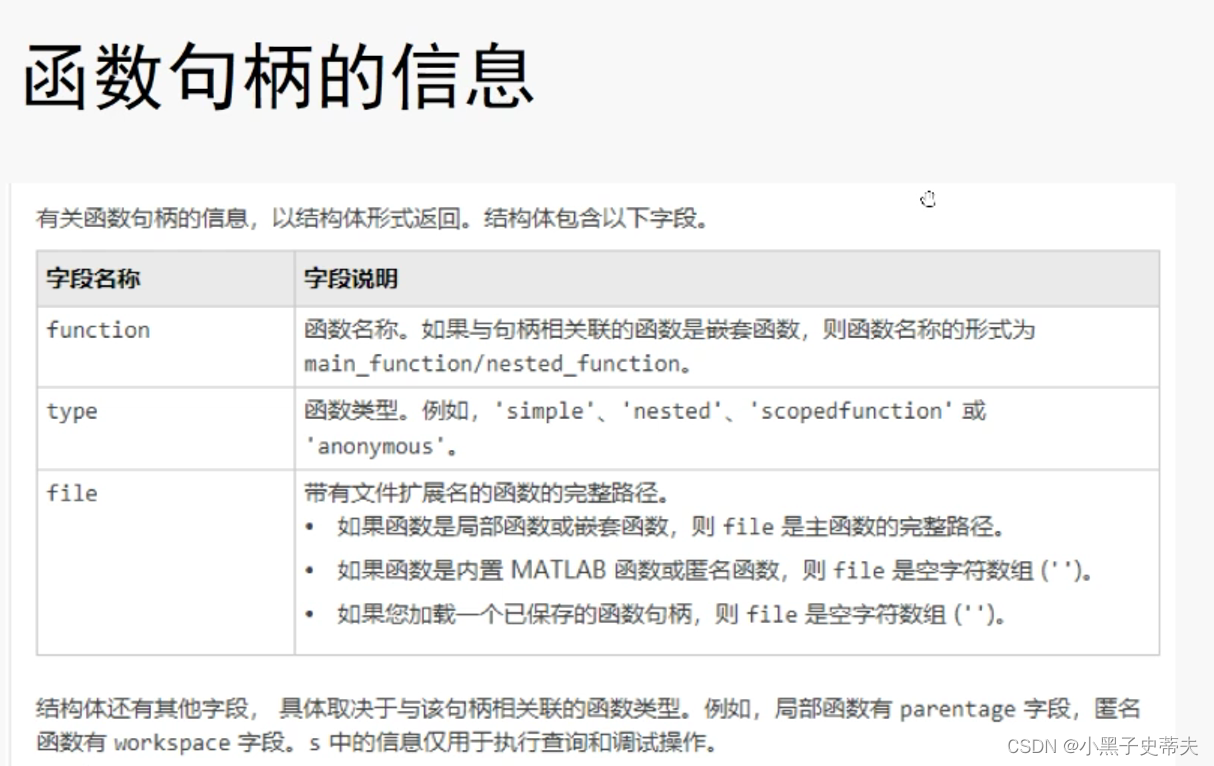

2. matlab中两种引号
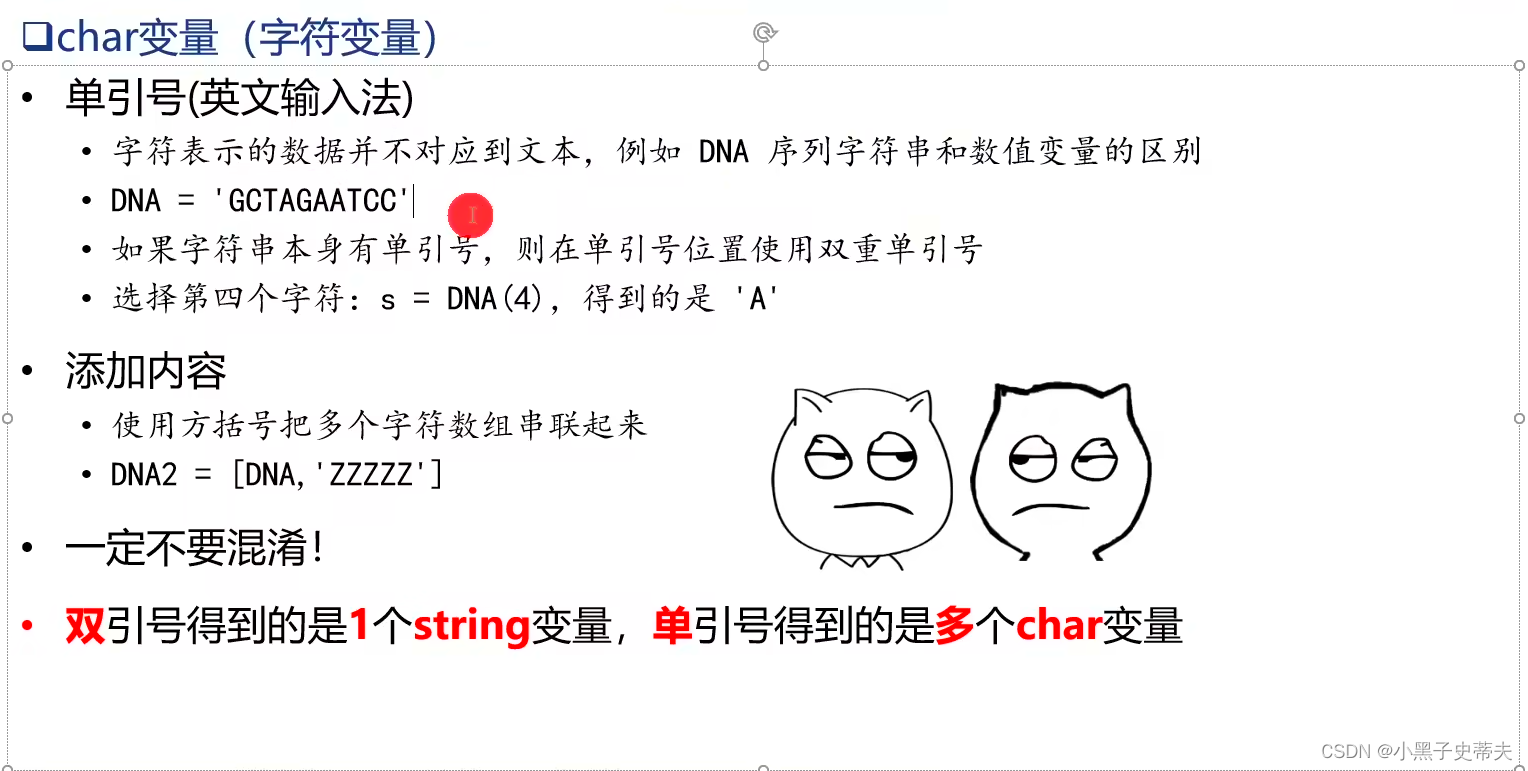
- string变量(字符串变量)

- char变量
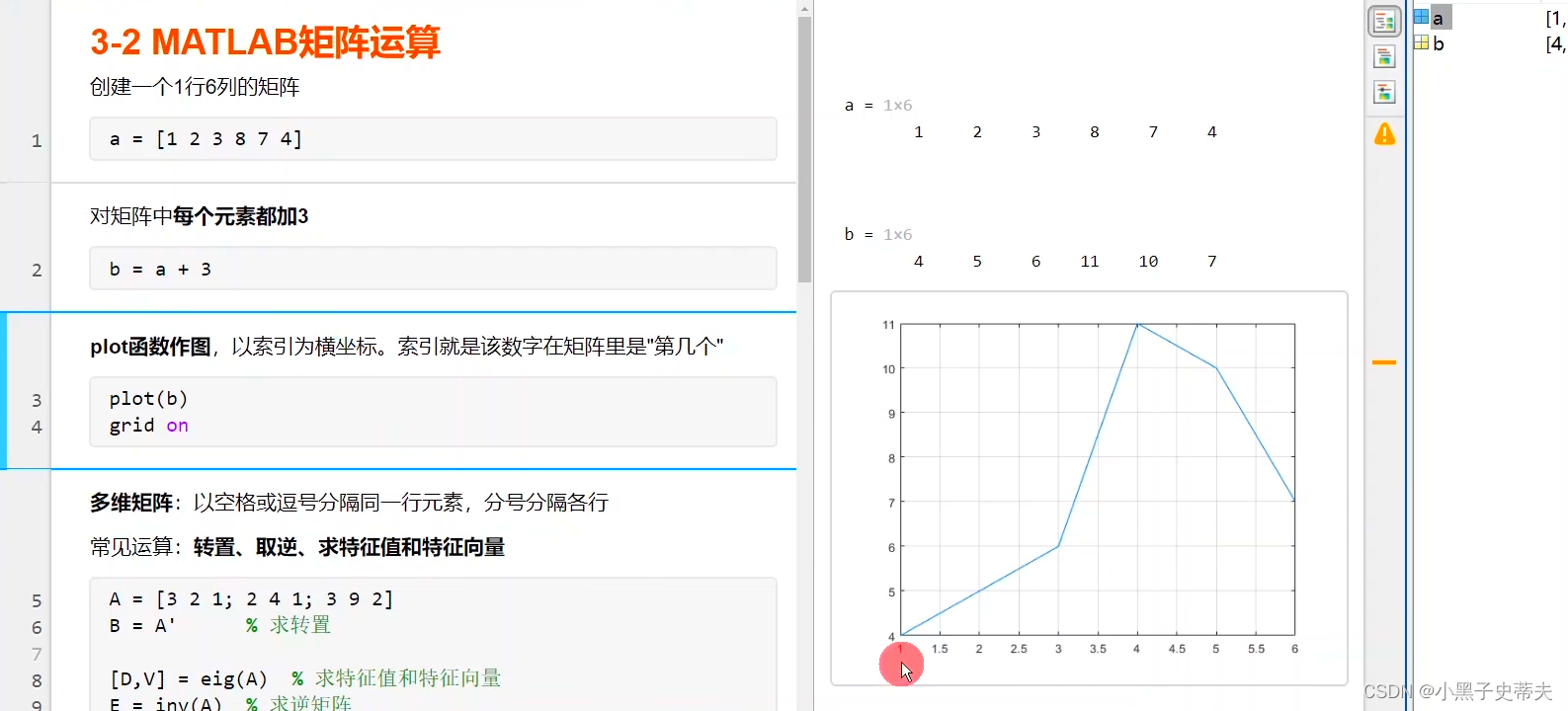
3. matlab矩阵及运算
3.1 特殊变量

-
生成单元数组

-
cell()函数,创建几×几的单元数组

-
定义数组
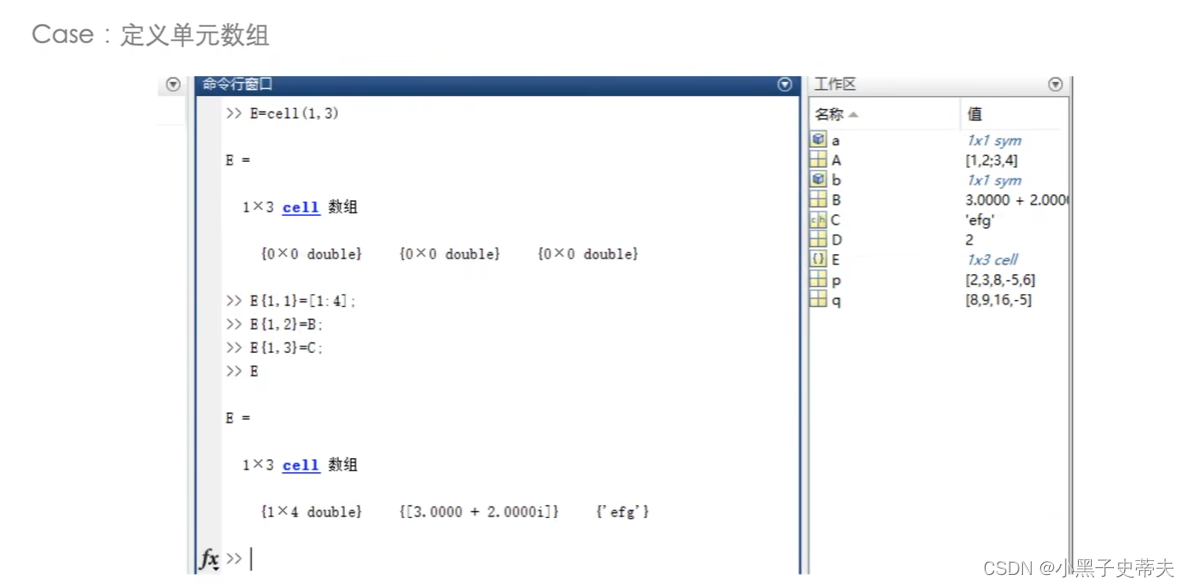
-
有关变量的函数


-
struct建立一个结构数组

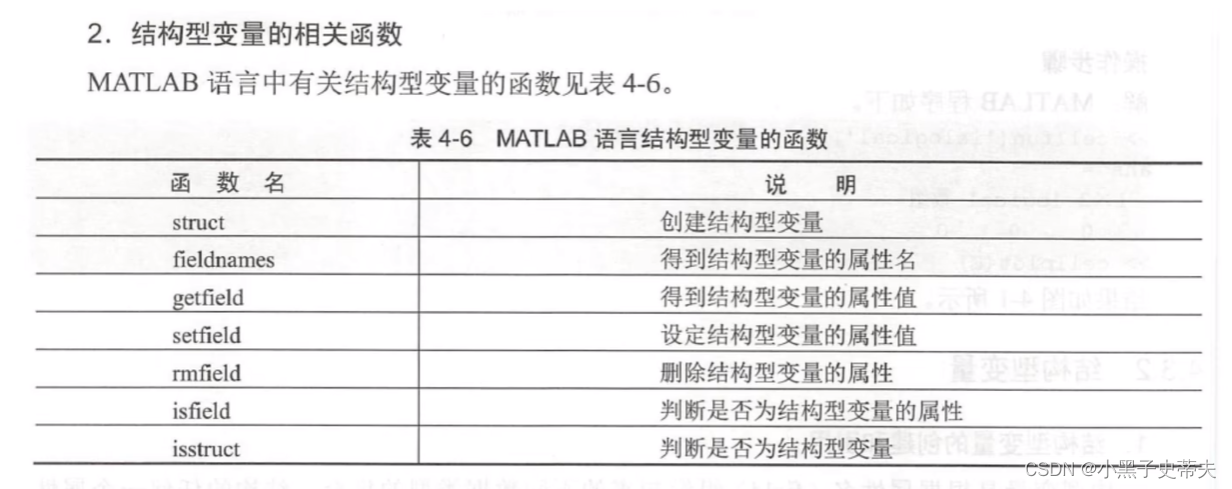
例子: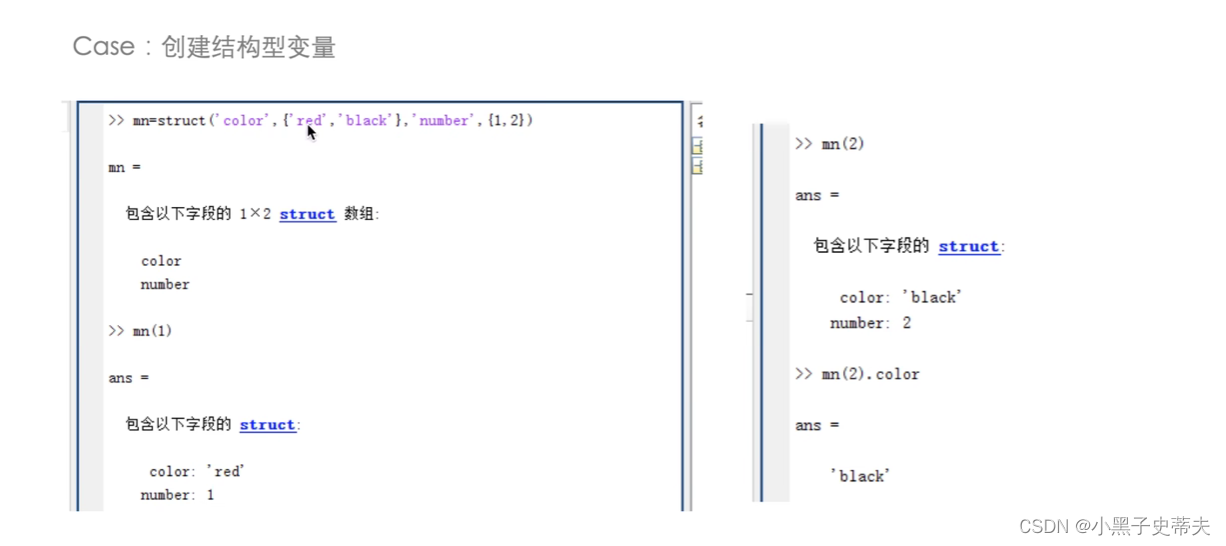
3.2多维矩阵


- 命令行
load+调用文件路径

- 也可以导入数据

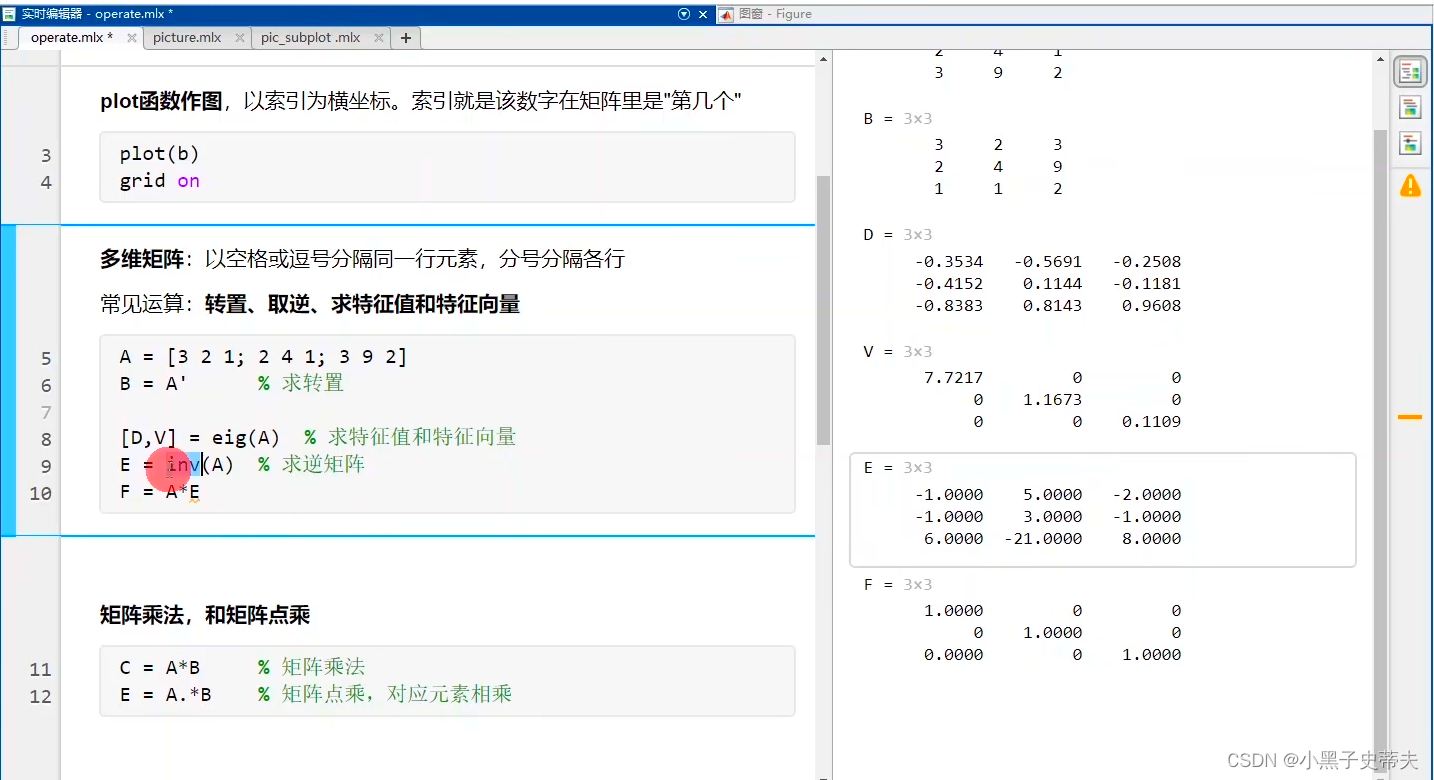
- 矩阵运算函数

3.3 点乘与乘 = 幂运算
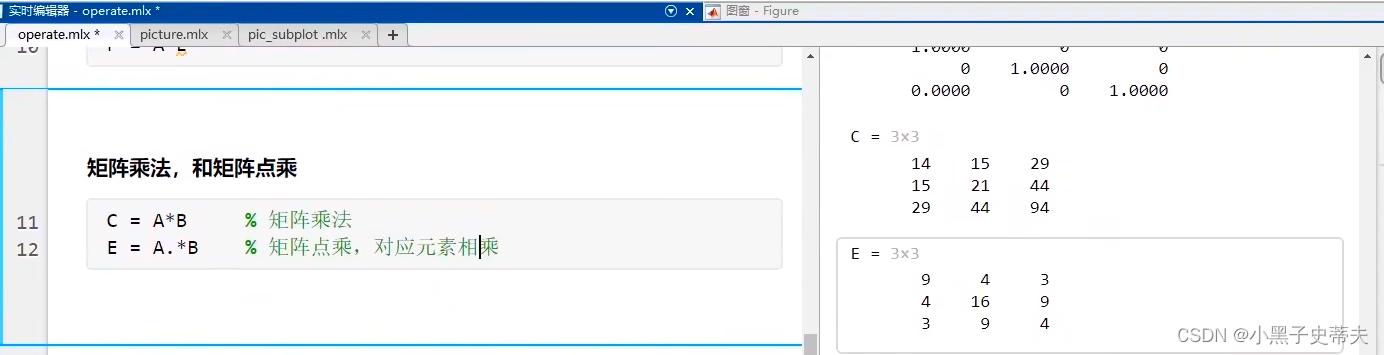

3.4 A*x=b求解
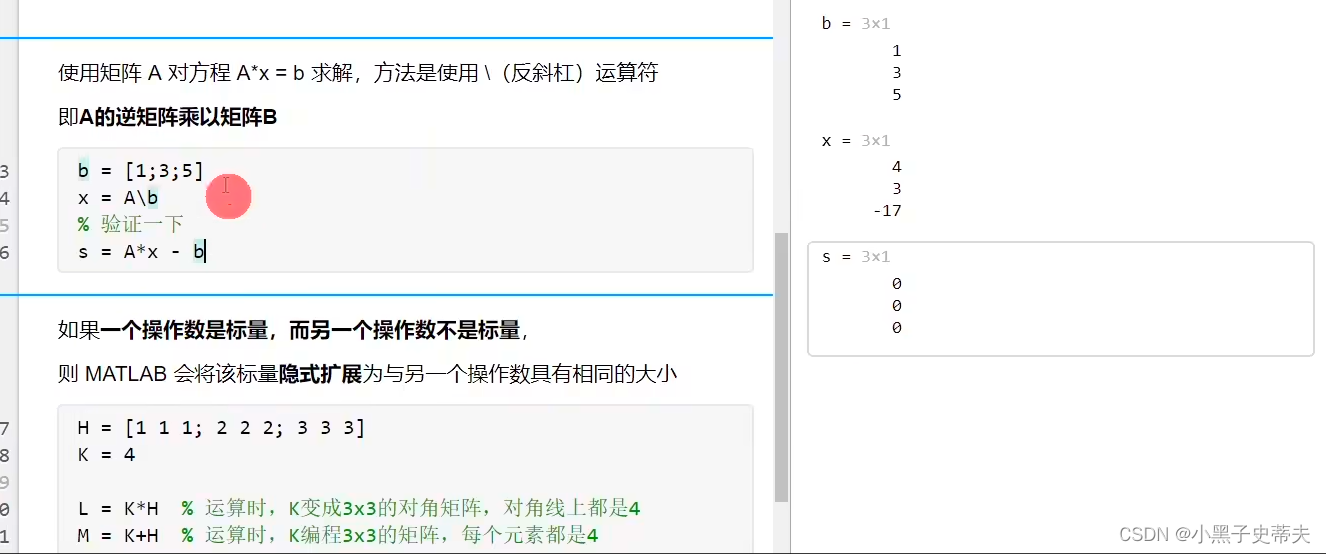
3.5 一个操作数是标量,而另一个操作上不是标量

不同维度的行向量和列向量相加:
matlab会根据缺少的地方补0
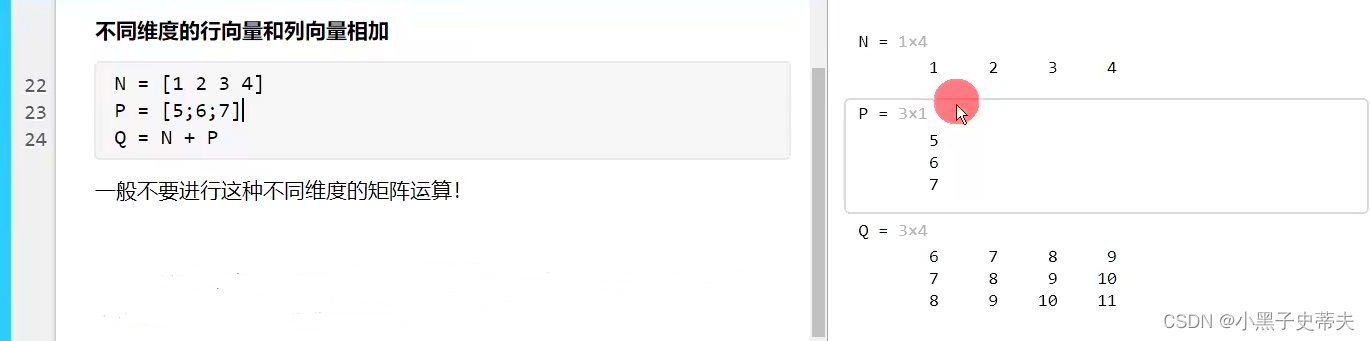
3.6 矩阵元素的修改
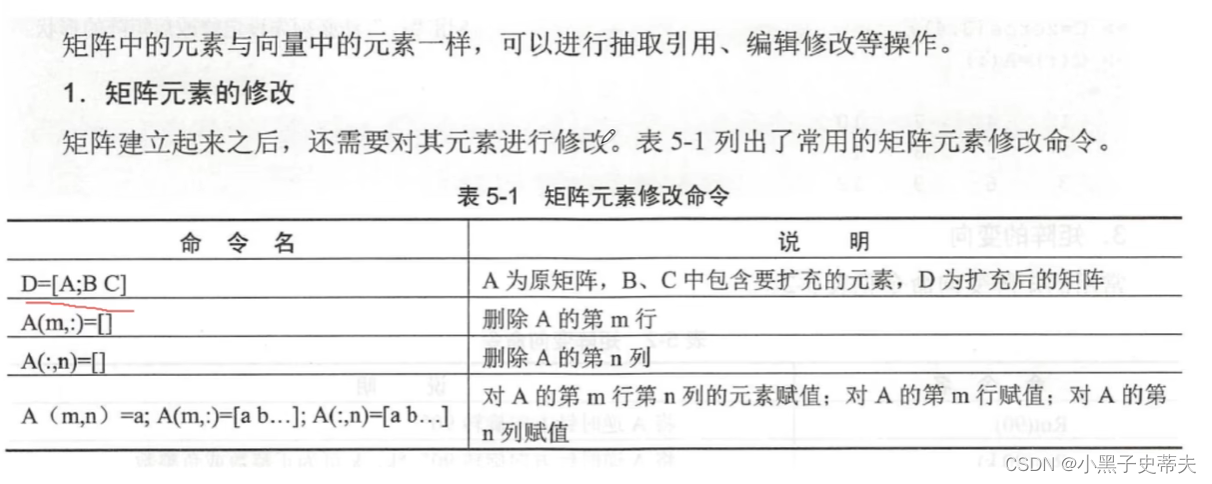

例子:
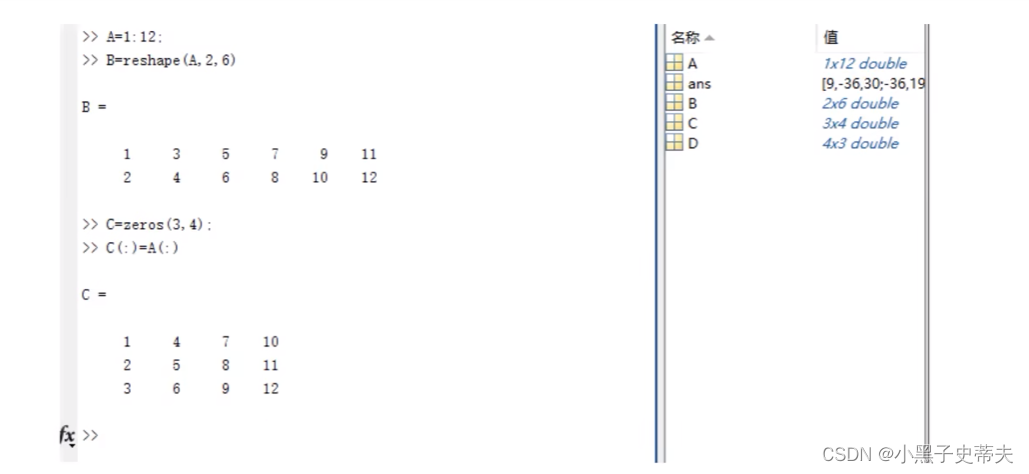
- 矩阵抽取


3.7 常用矩阵函数

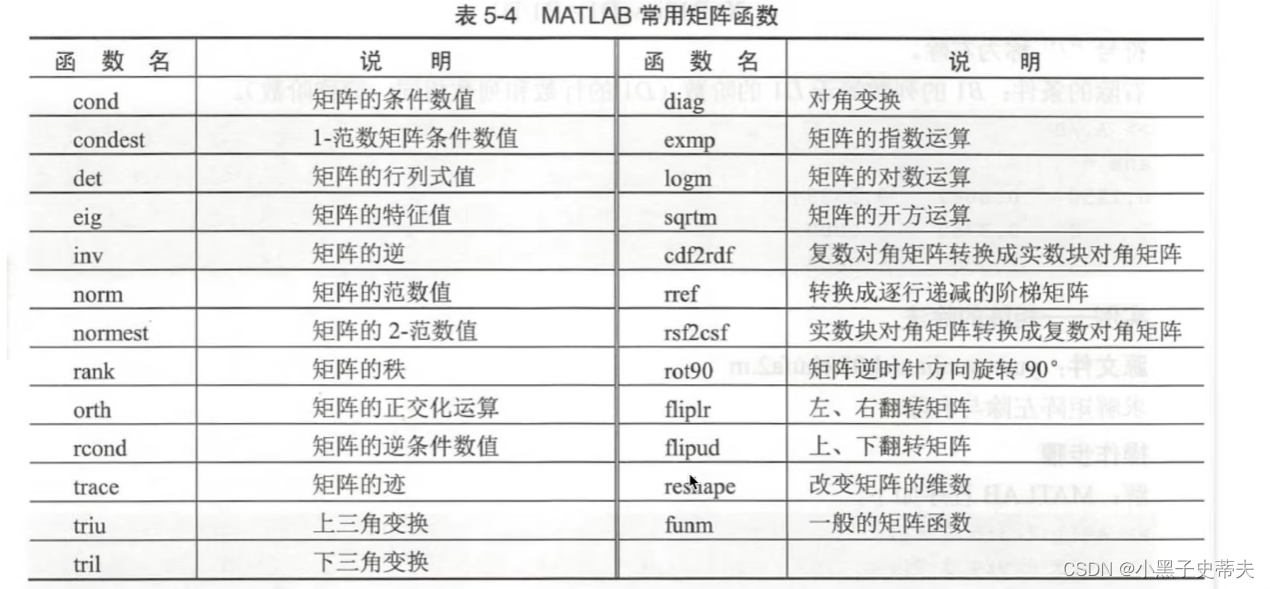

-
svd 矩阵奇异值运算

例子: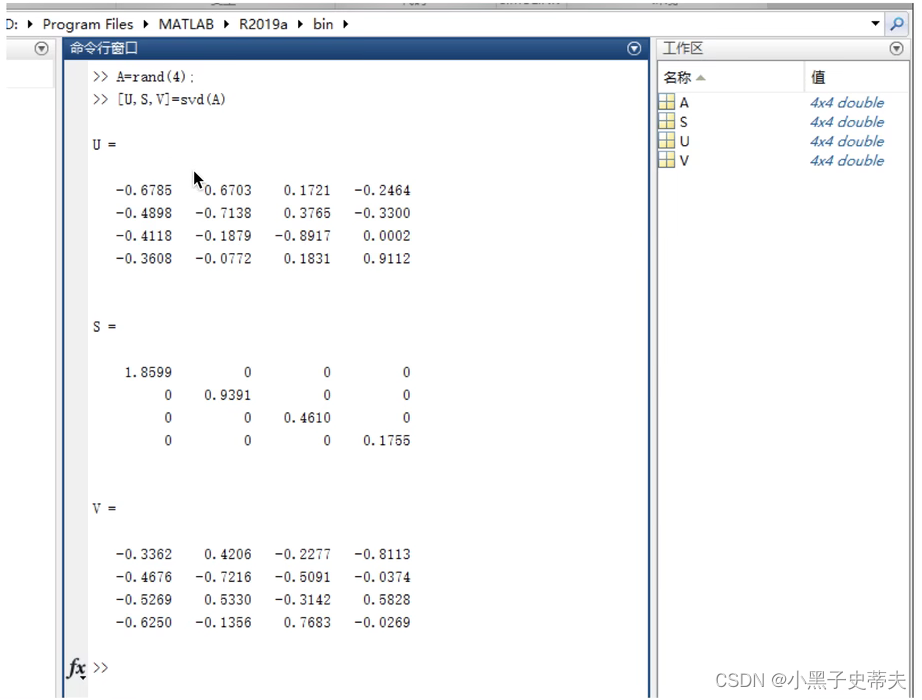

-
方程求解

3.8 matlab符号运算
-
subs函数简单来说就是替换变量

例子:
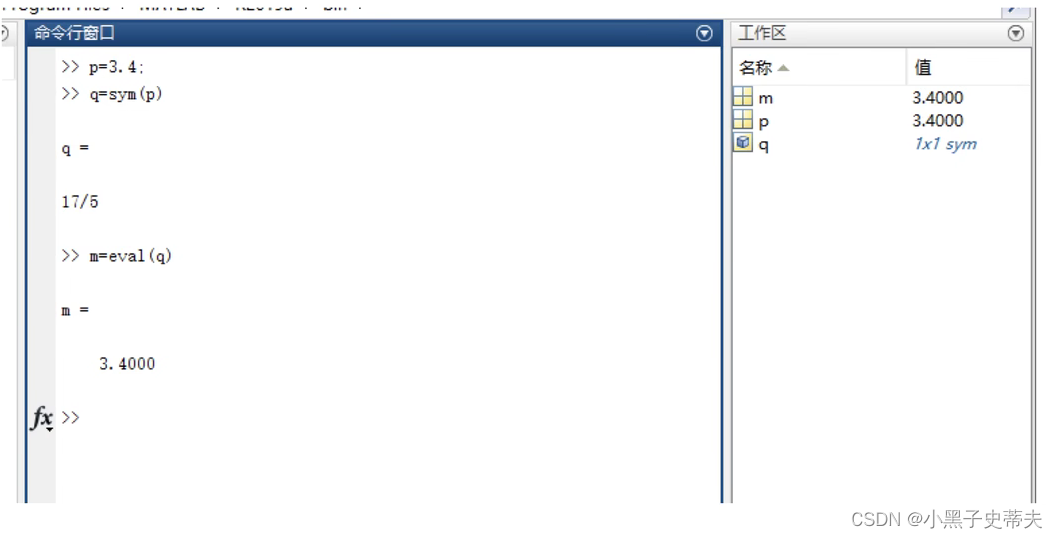
-
digits函数:求近似 与 vpa函数:在设置的有效个数下求

例子: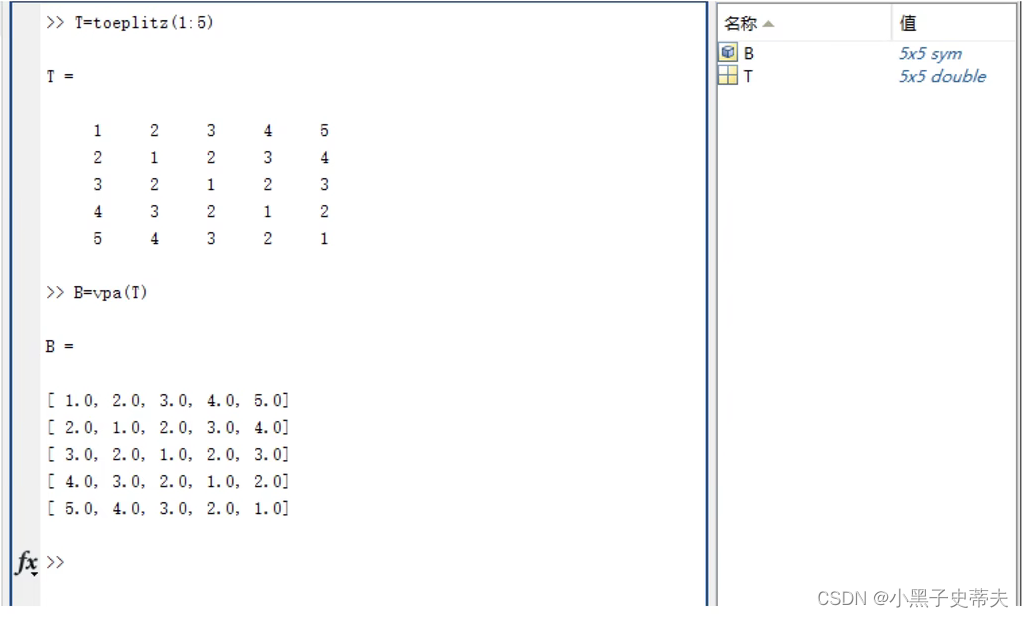
-
sym 生成符号矩阵

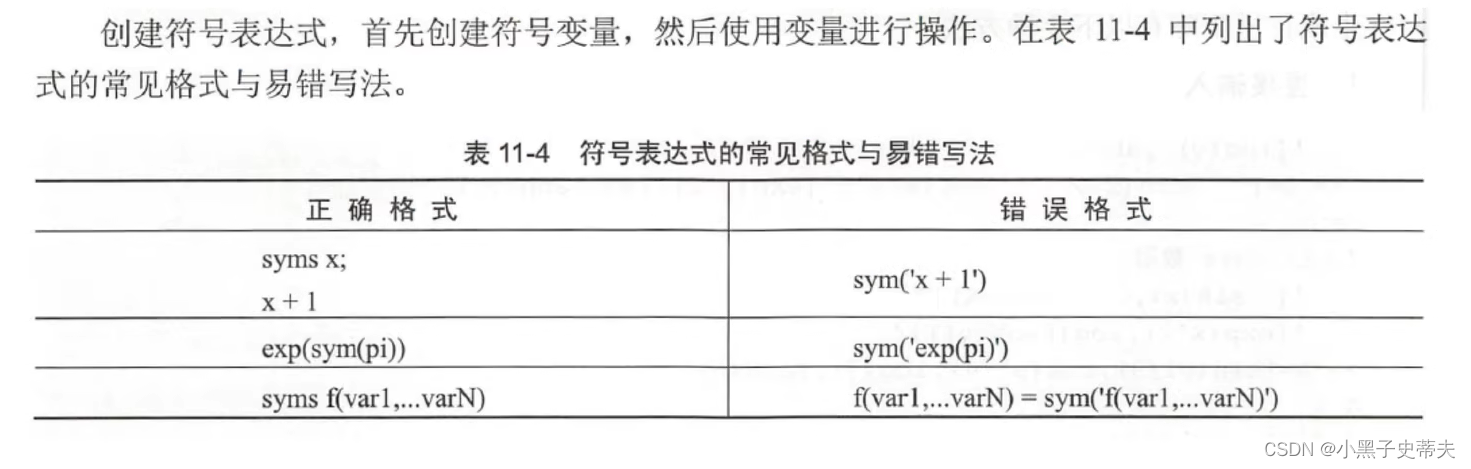
例子:

-
数值矩阵转换为符号矩阵


-
factor 函数因式分解 和 expand 函数式子展开


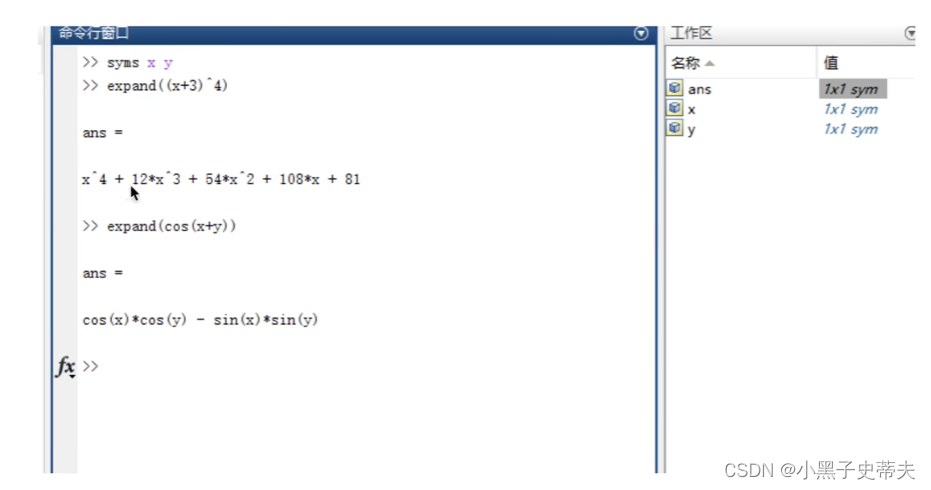
-
符号简化simple 与 分式通分numden

上诉n为分母,d为分子
例子:


-
horner§ 用于提取多项式共同因子
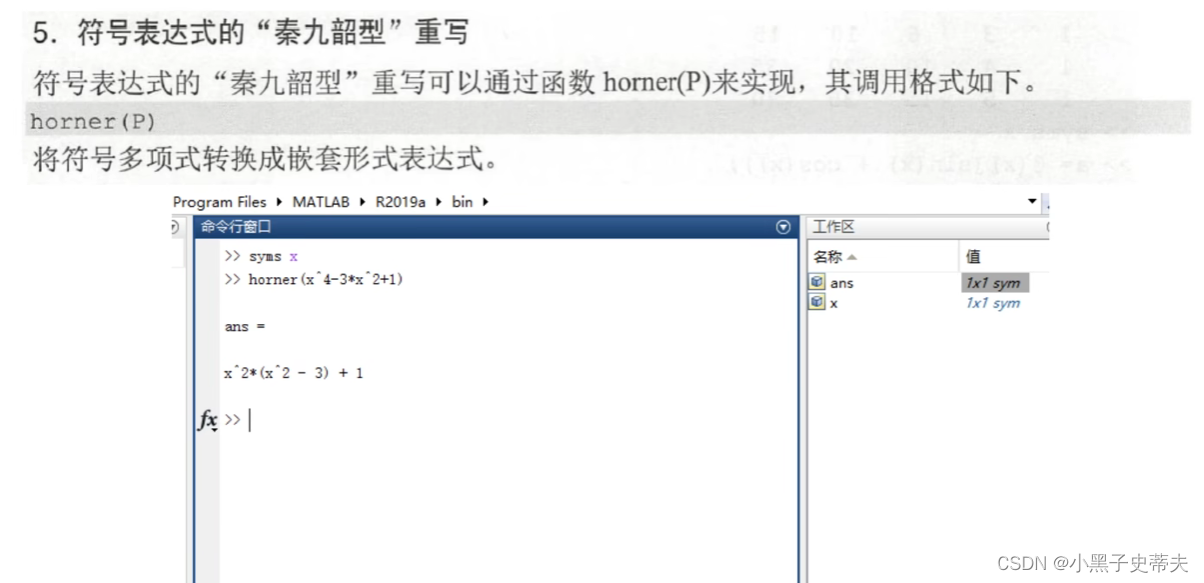 例子:
例子:

4. matlab的绘图
4.1 线图plot函数

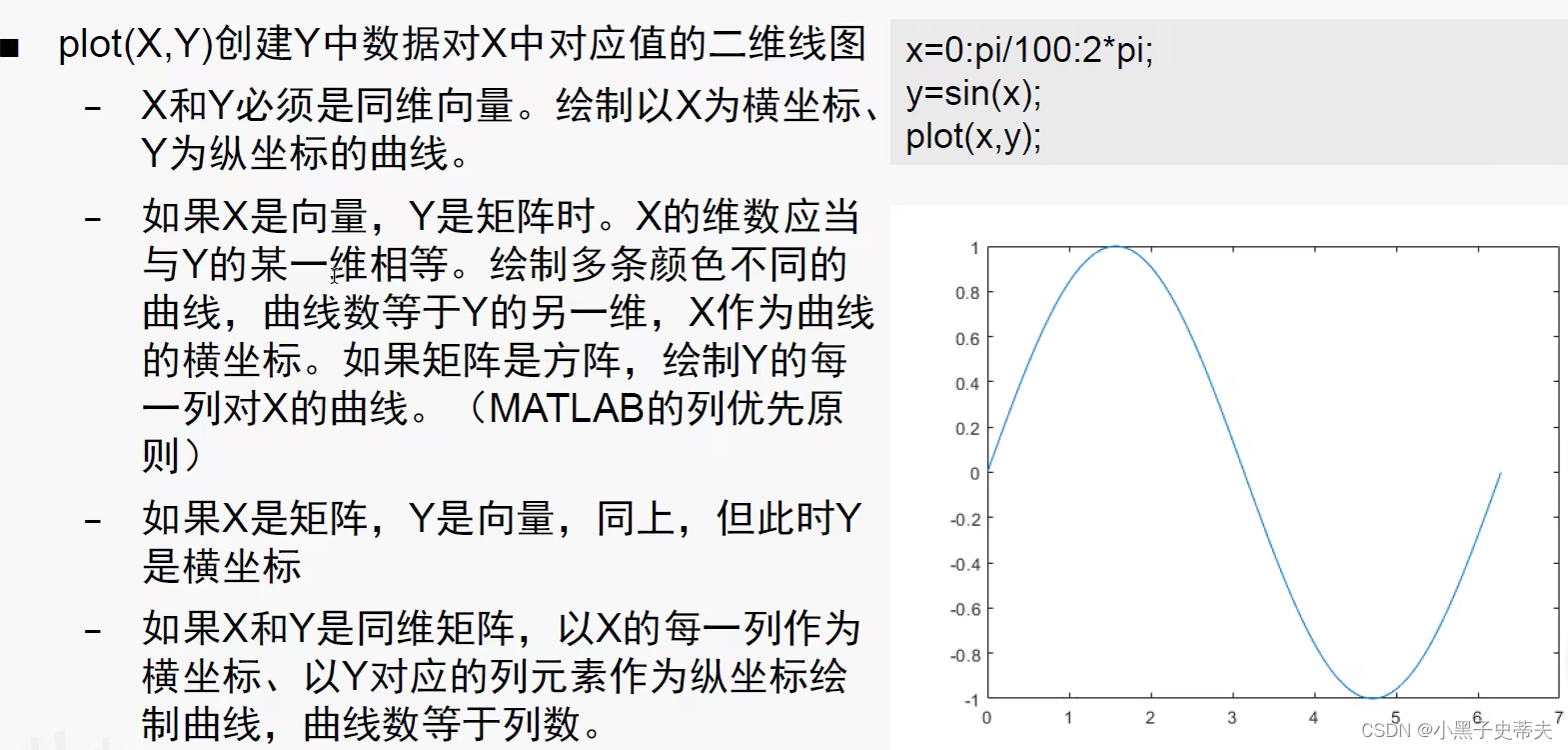

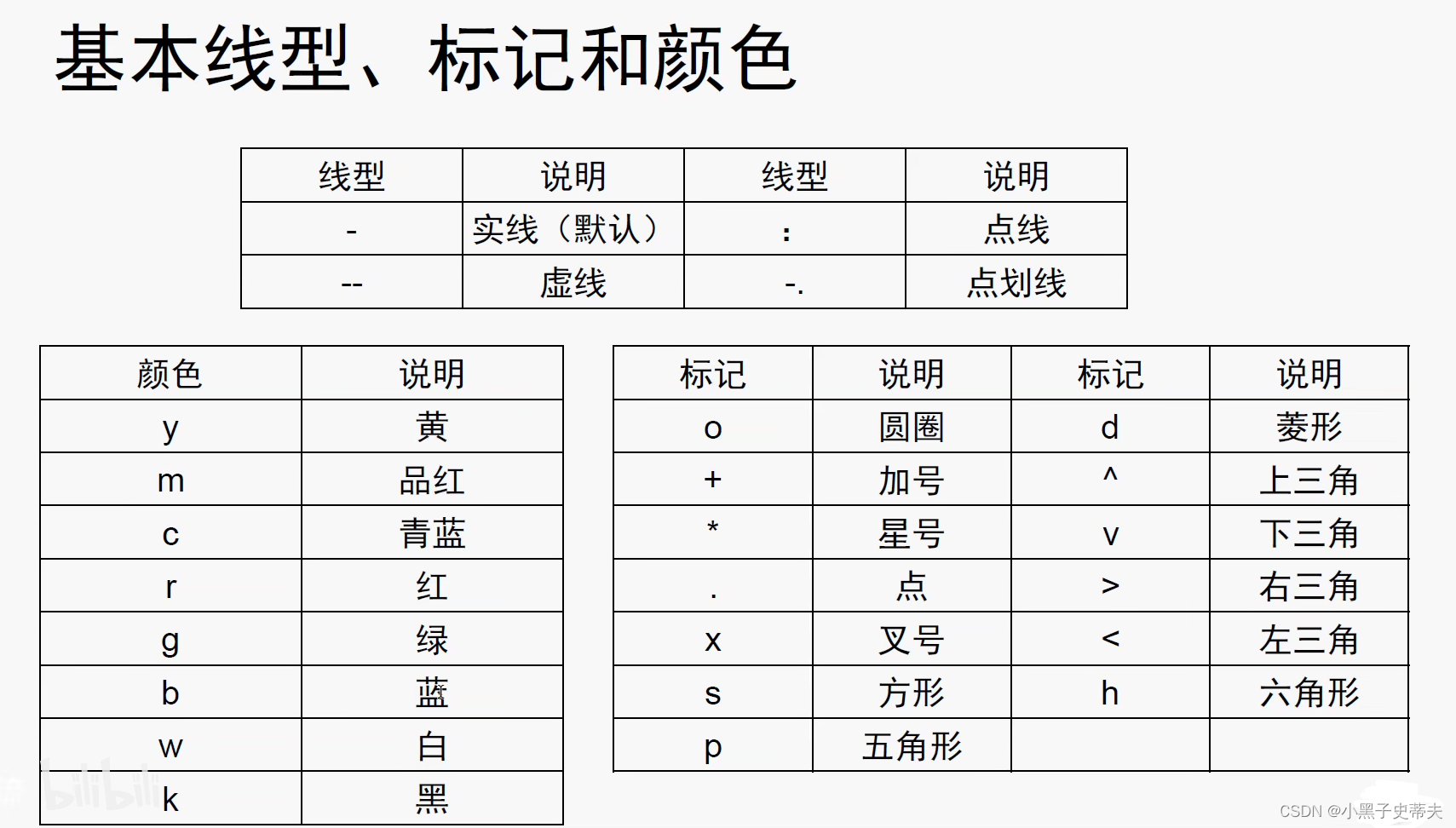
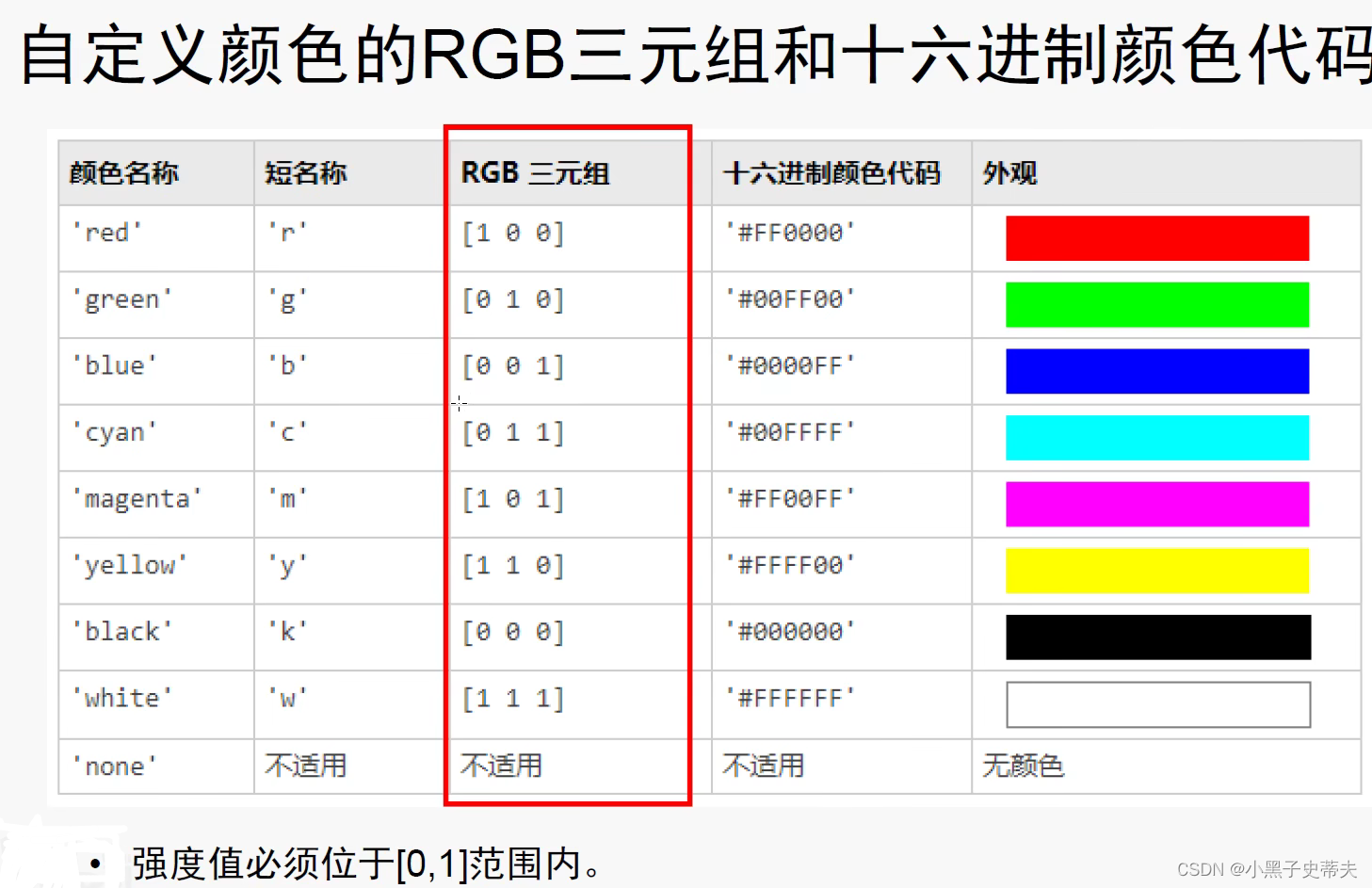
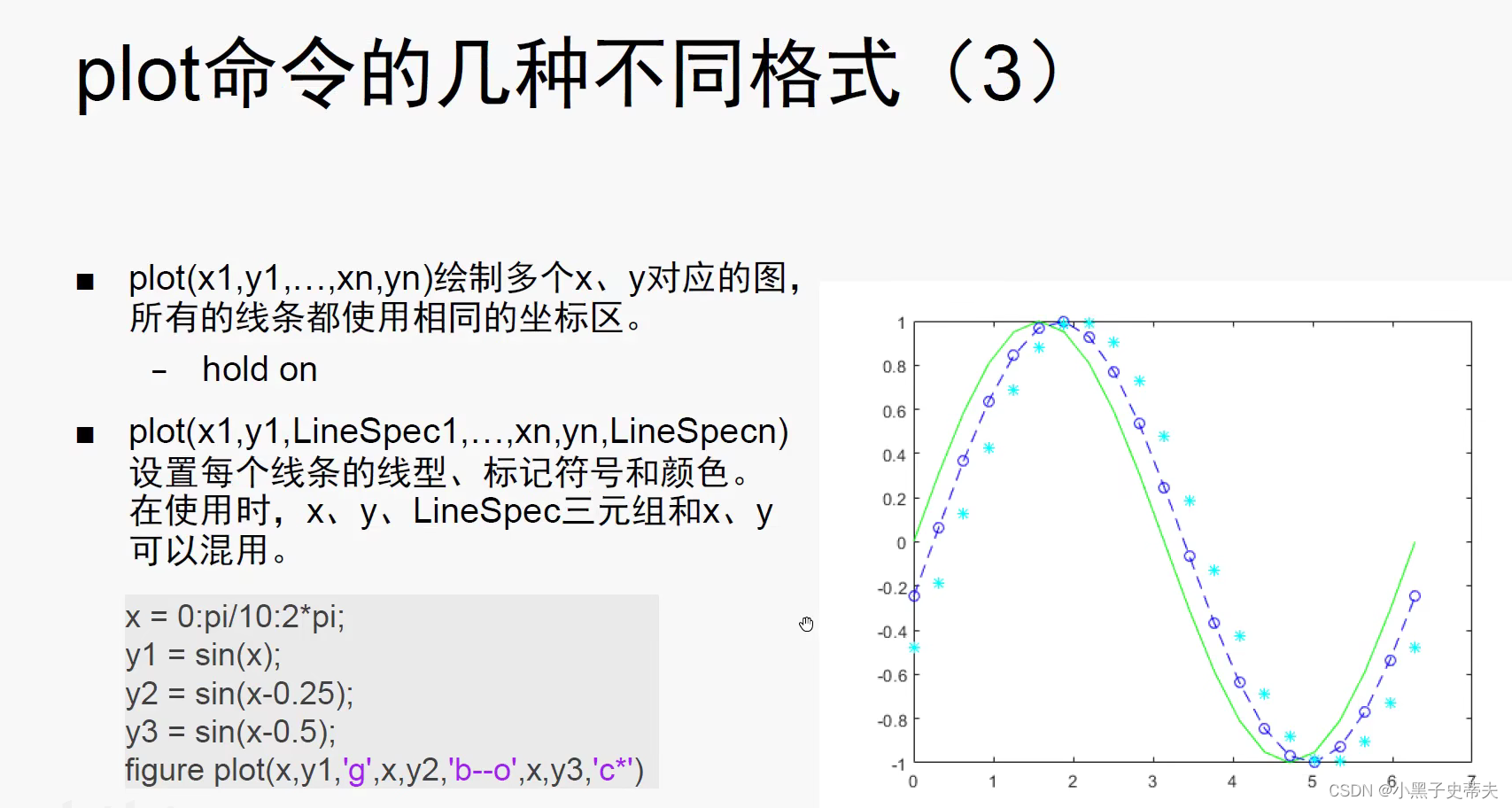
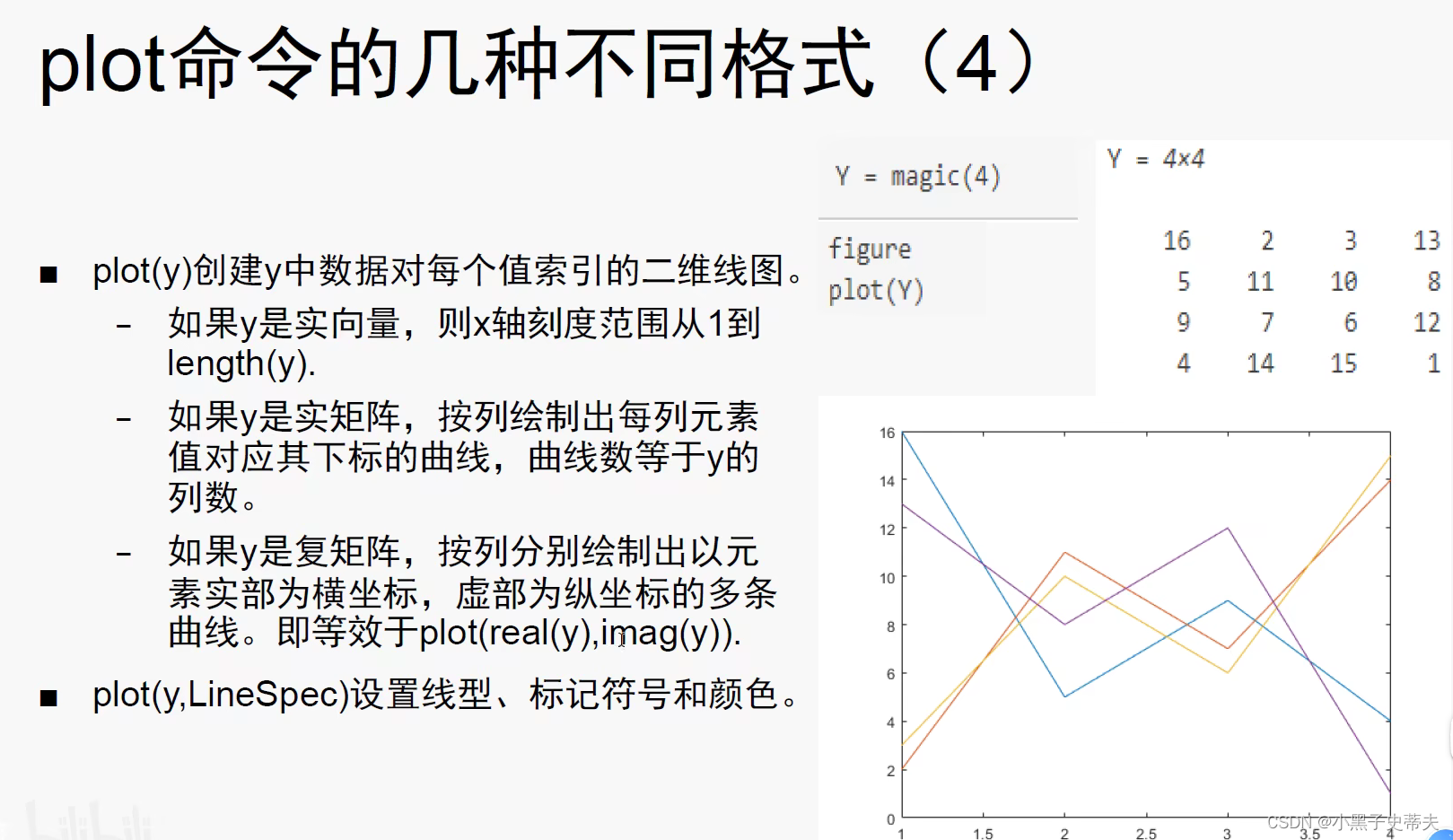
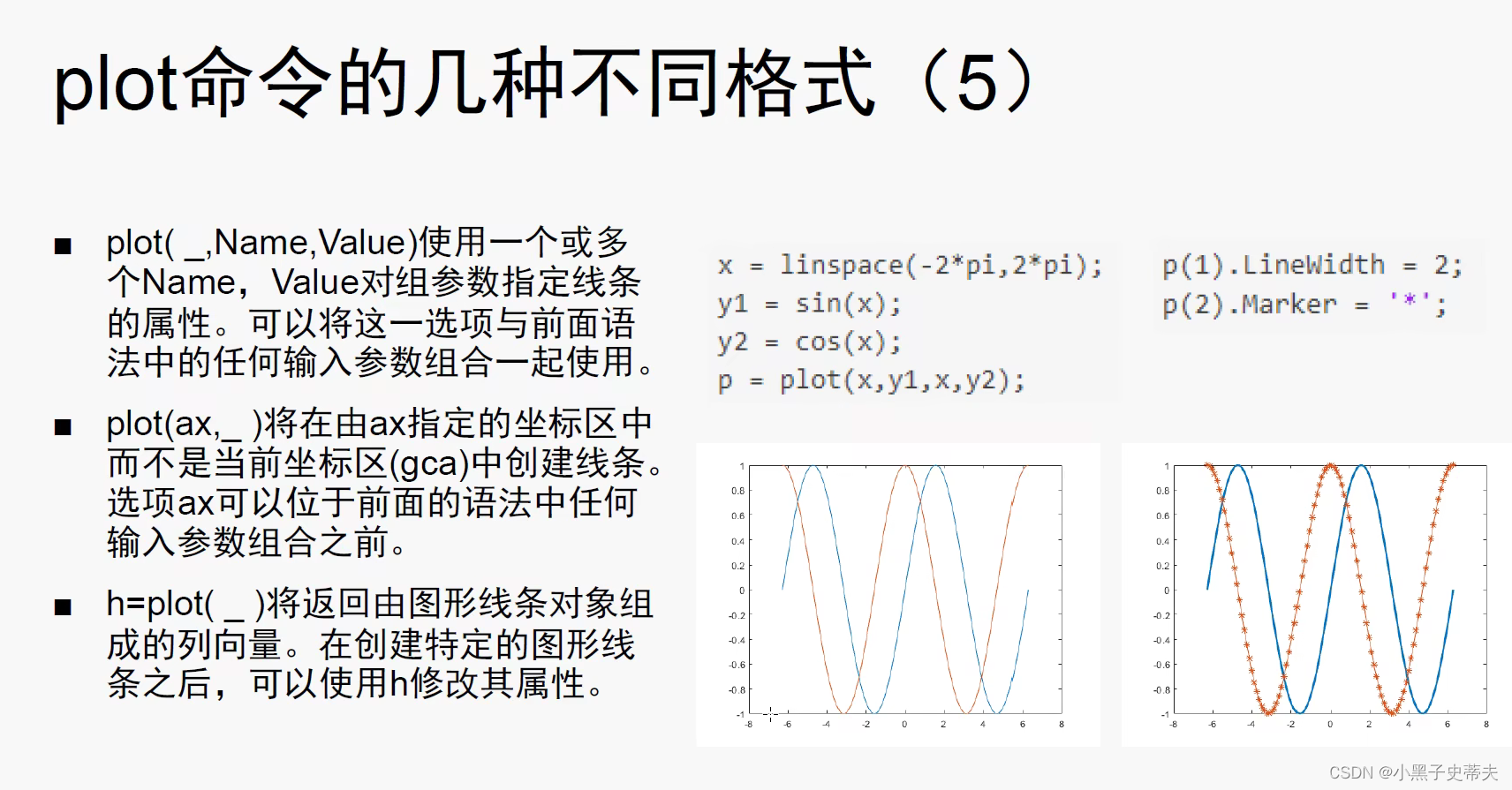
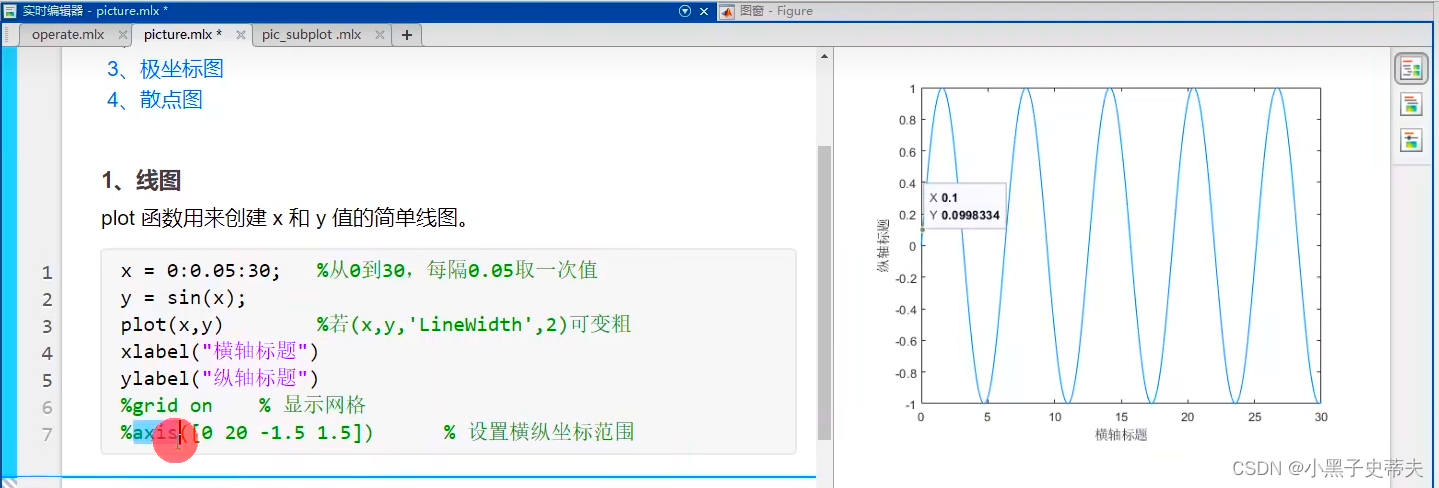
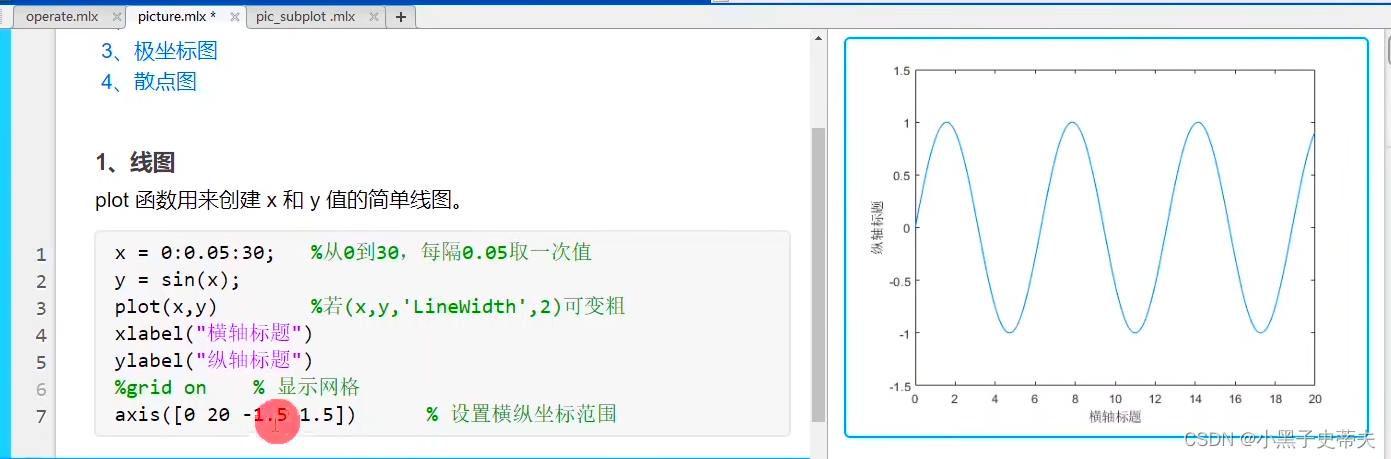
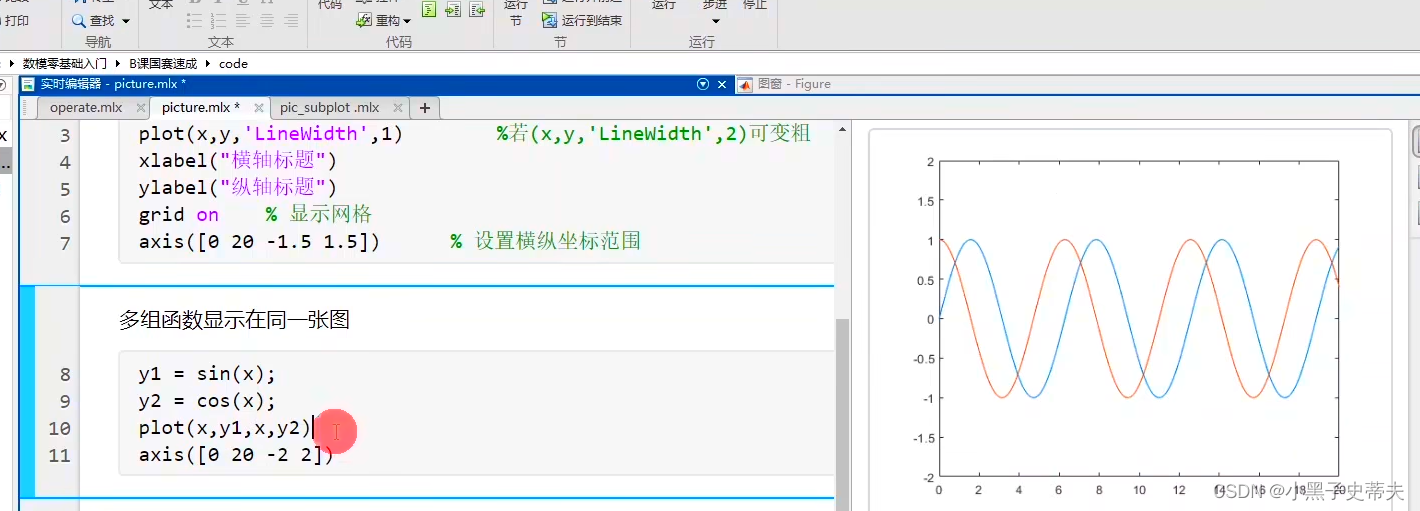
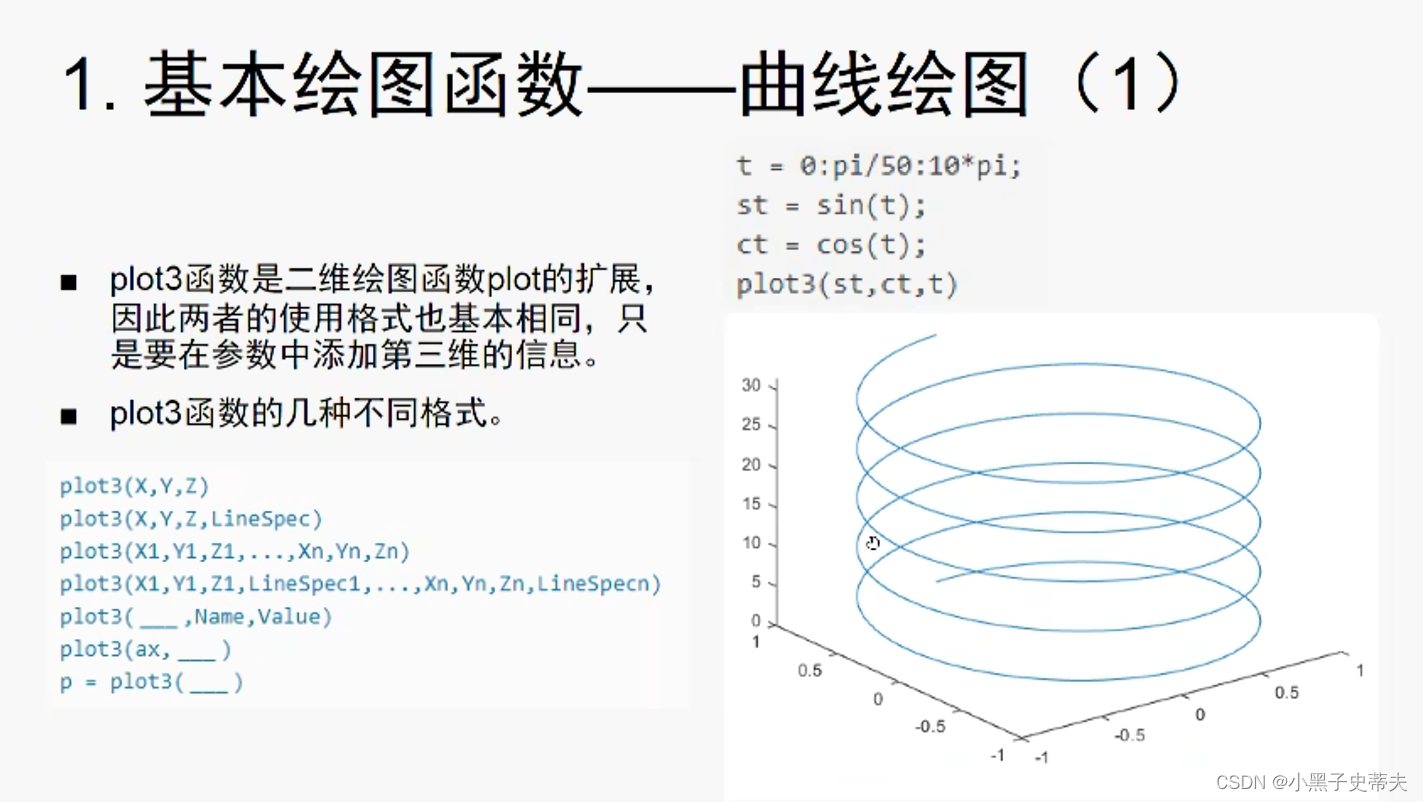
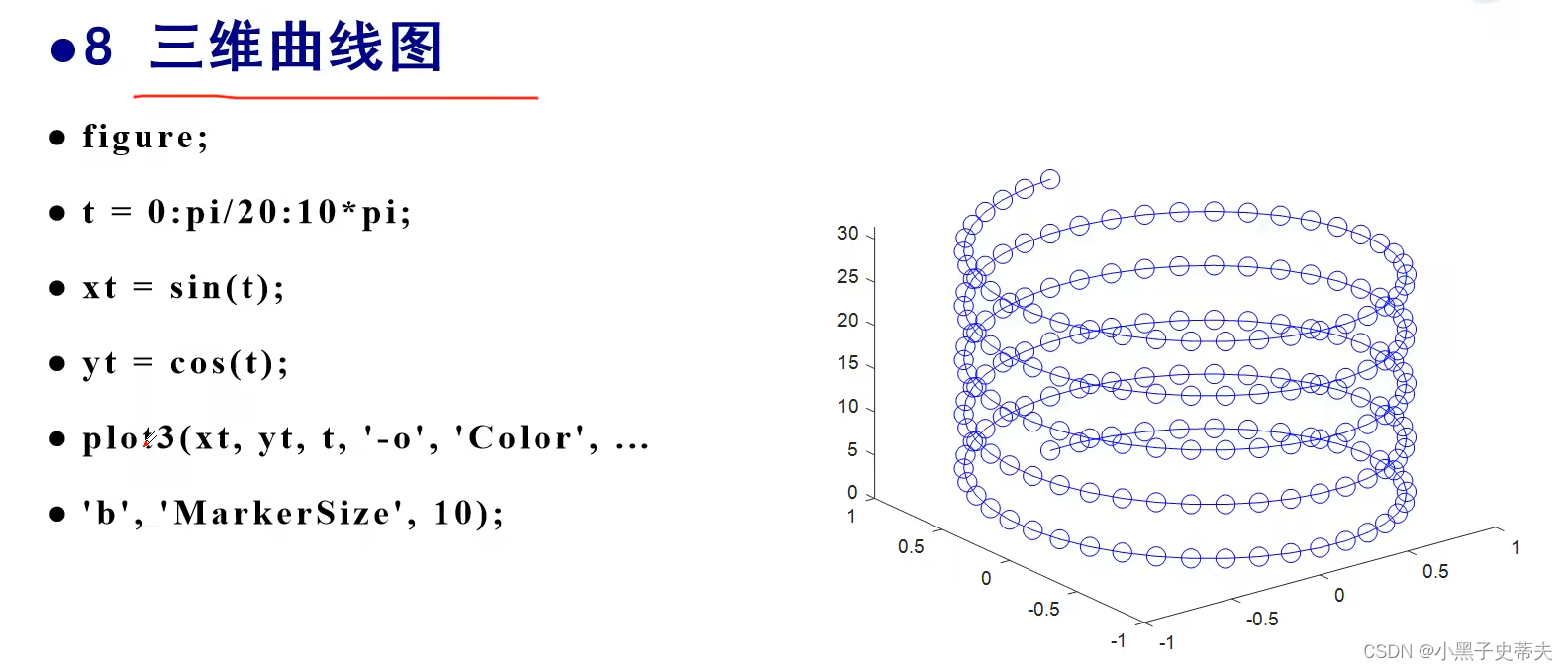
4.1.2 三维曲线绘图 plot3
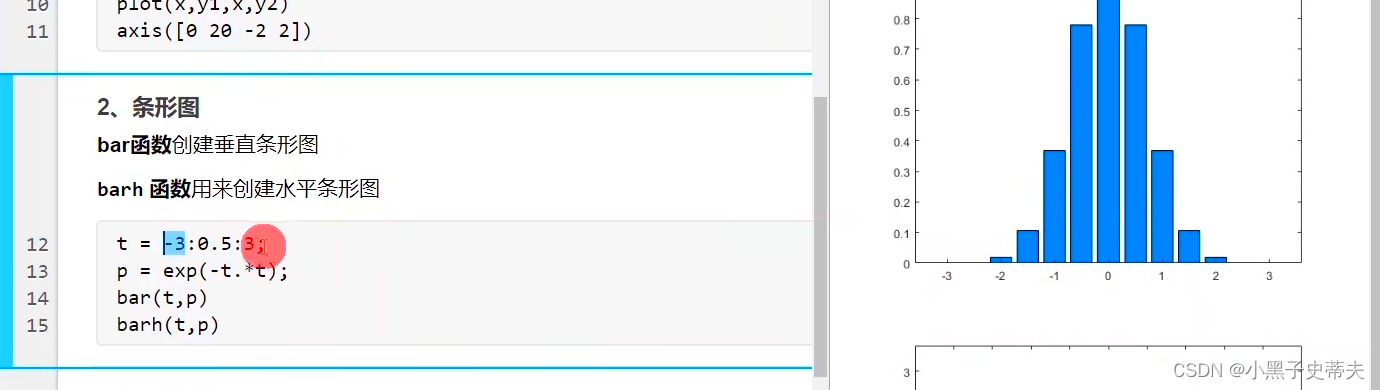
4.2 条形图bar函数


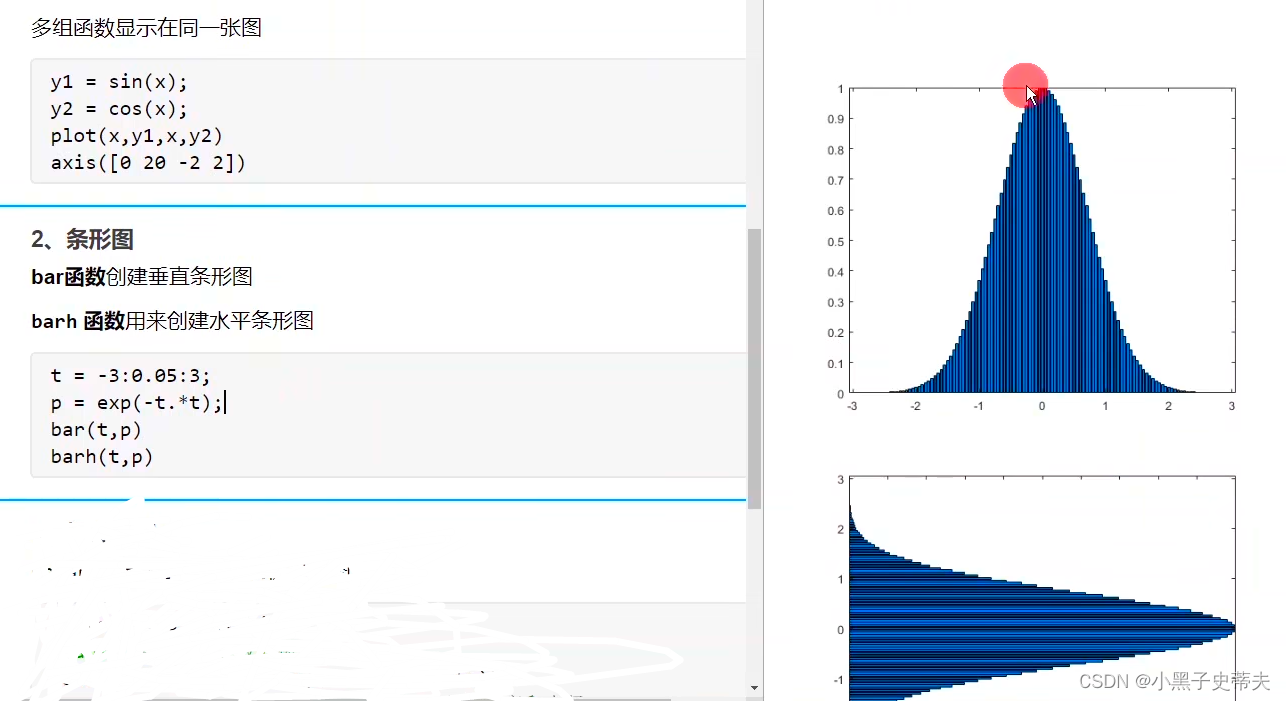
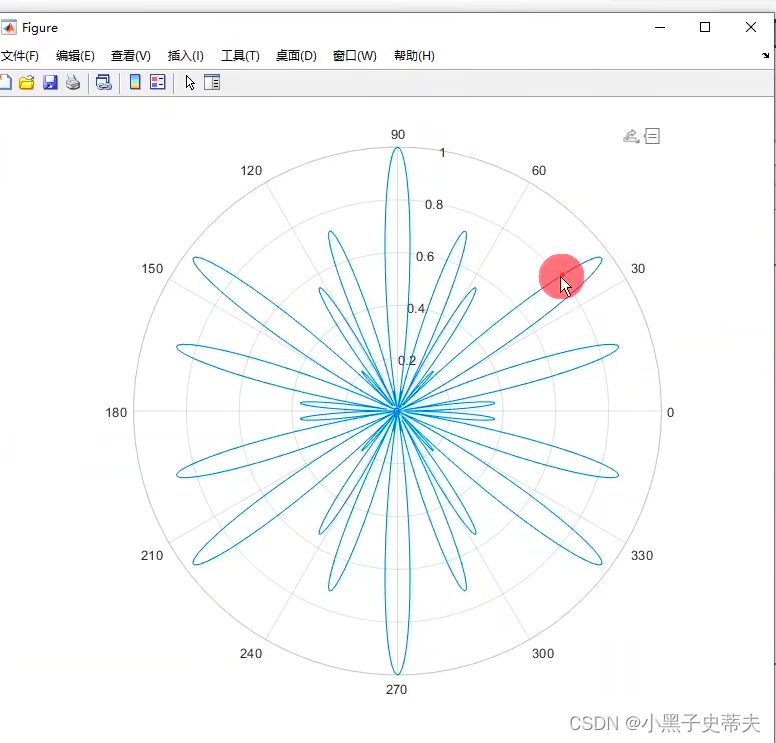
4.3 极坐标图polarplot函数




polarplot函数用来绘制极坐标图
theta = e:e.e1:2*pi;
% abs求绝对值或复数的模
radi = abs(sin(7*theta).*cos (10*theta));polarplot(theta,radi)
%括号内是弧度和半径
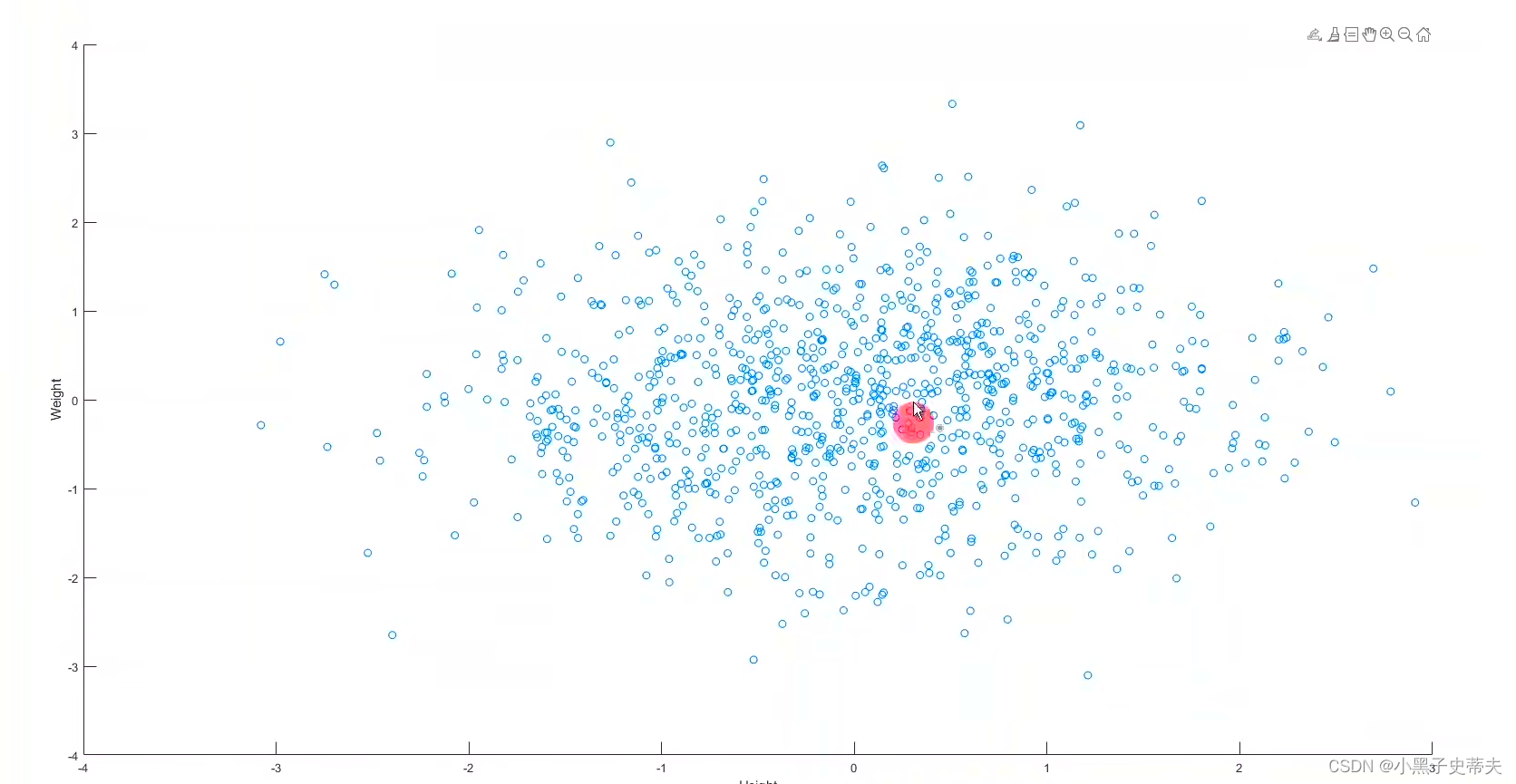
4.4 散点图scatter函数
scatter函数用来绘制×和y值的散点图
Height = randn ( 1000,1);
weight = randn (1000,1);
scatter(Height,weight)
xlabel( 'Height ')
ylabel( ' weight ')
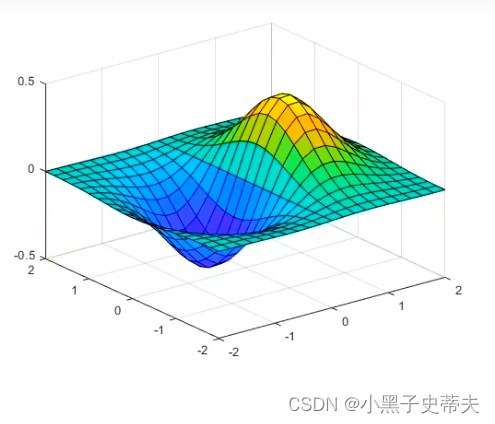
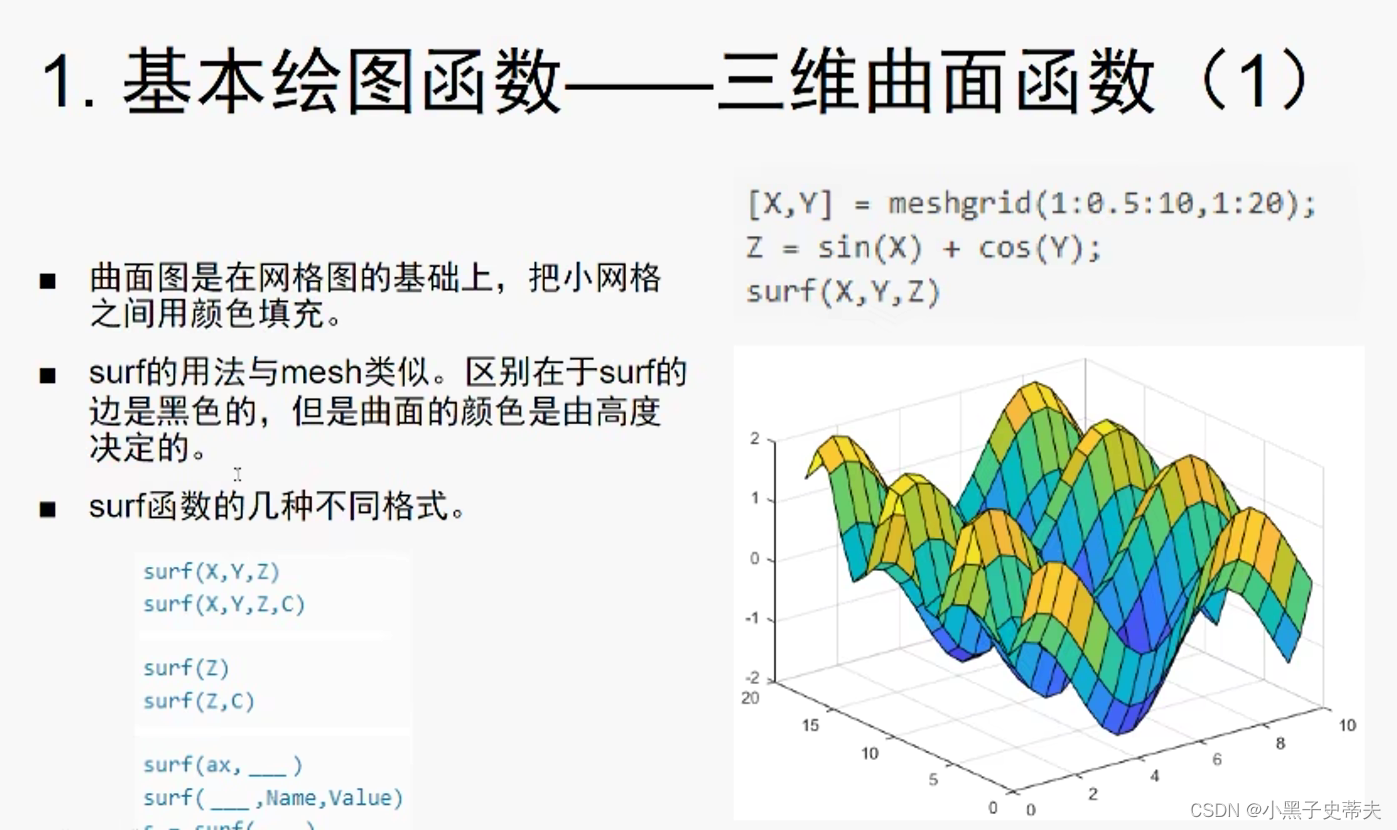
4.5 三维曲面图surf
surf函数可用来做三维曲面图。一般是展示函数z=z(x,y)的图像。
首先需要用meshgrid创建好空间上(x,y)点。
[×,Y] = meshgrid( -2:0.2:2); %采点
%Z= x.^2 +Y.^2
z = x.*exp( -x.^2-Y.^2);
surf(×,Y,z);
%colormap hsv% colormap设置颜色,可跟winter、summer等,hsv是一种颜色模型
%colorbar
- 采集点密集

- 采集点稀疏
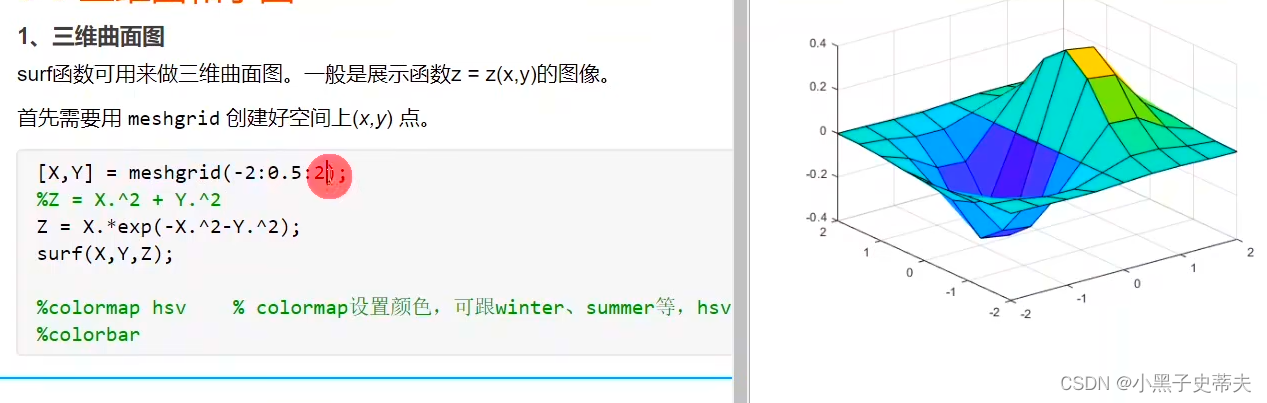
- 色调
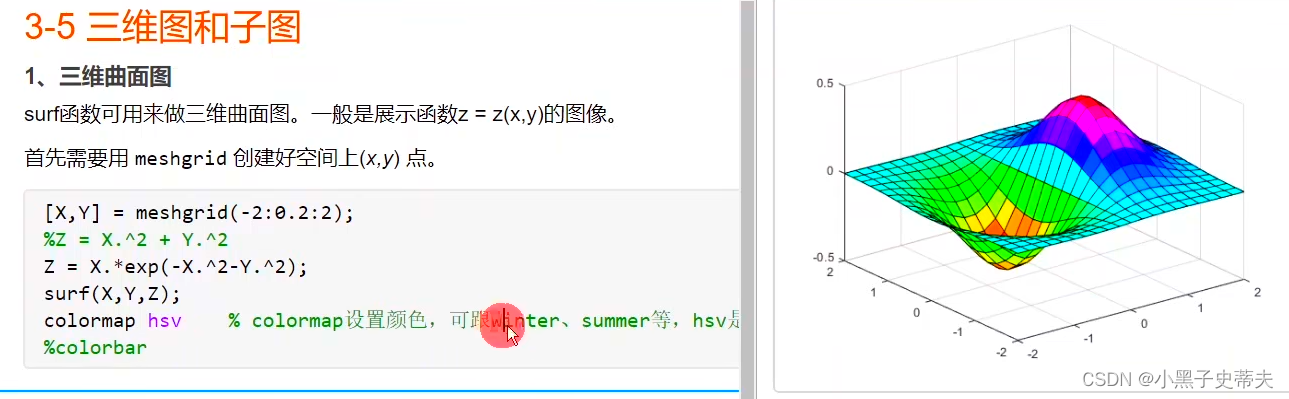
- 颜色调柱

- 颜色调柱
4.6 子图subplot函数

使用subplot函数可以在同一窗口的不同子区域显示多个绘图
theta = 0:e.e1:2*pi;
radi = abs(sin(2*theta).*cos ( 2*theta) );
Height = randn( 1000,1);
weight = randn( 100e,1);
subplot(2,2,1); surf(×.^2); title( ' 1st' );
subplot(2,2,2); surf(Y.^3); title( ' 2nd ' ) ;
subplot(2,2,3); polarplot(theta,radi); title( ' 3rd ' );
subplot(2,2,4) ;scatter(Height,weight); title( ' 4th');
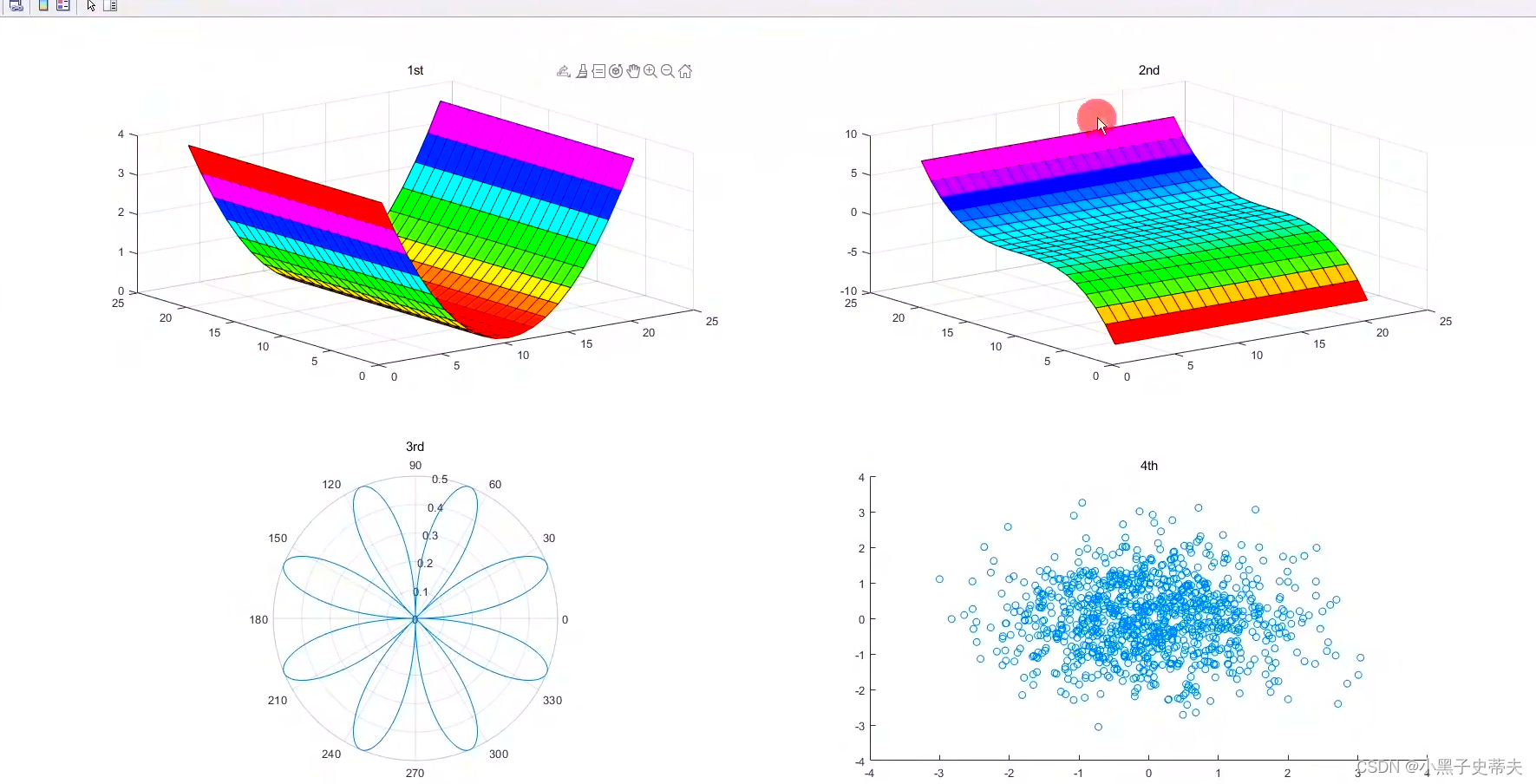
4.7 fplot精确绘图



4.8 ezplot符号函数绘图

4.9 plotyy 和 yyaxis
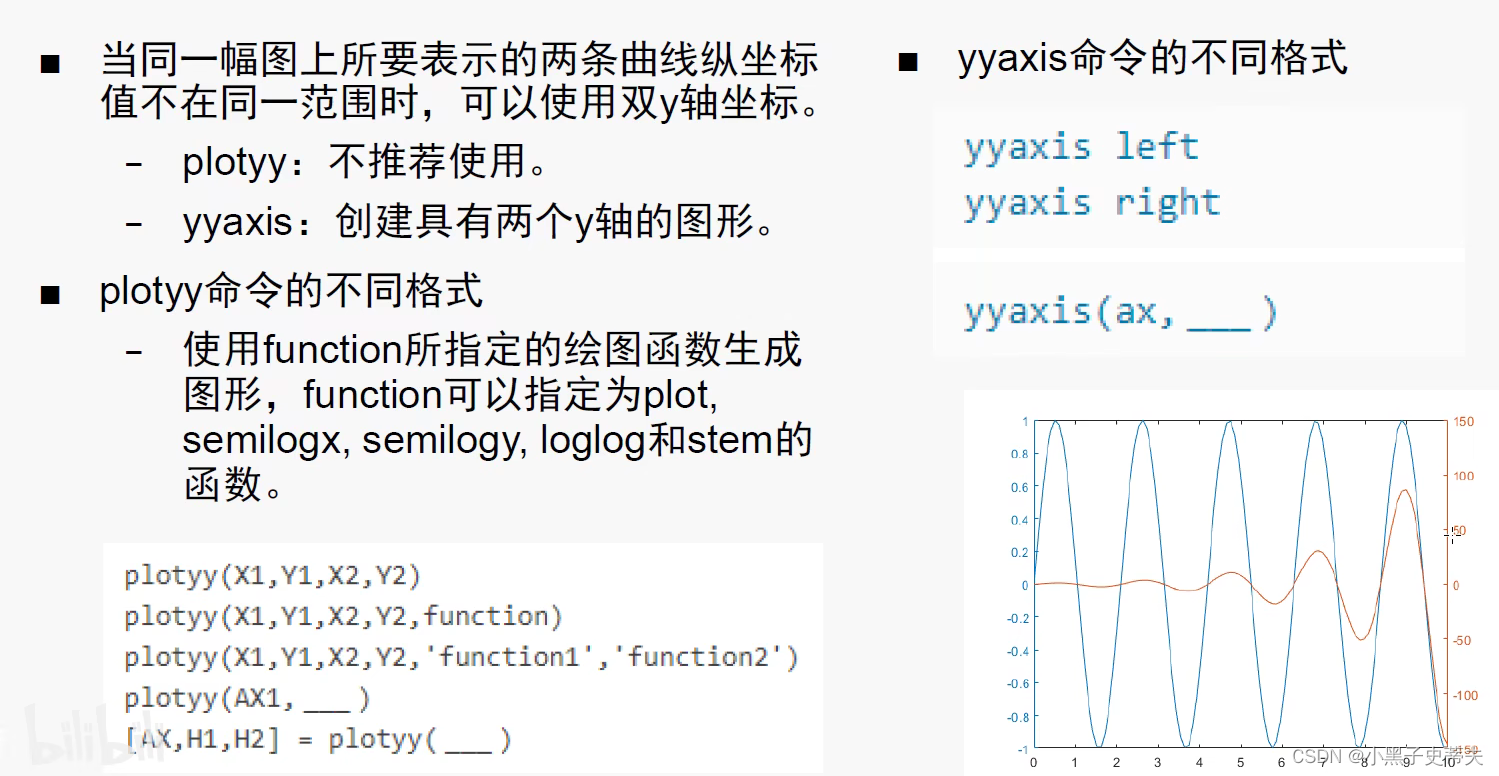
4.10 figure 创建图形窗口

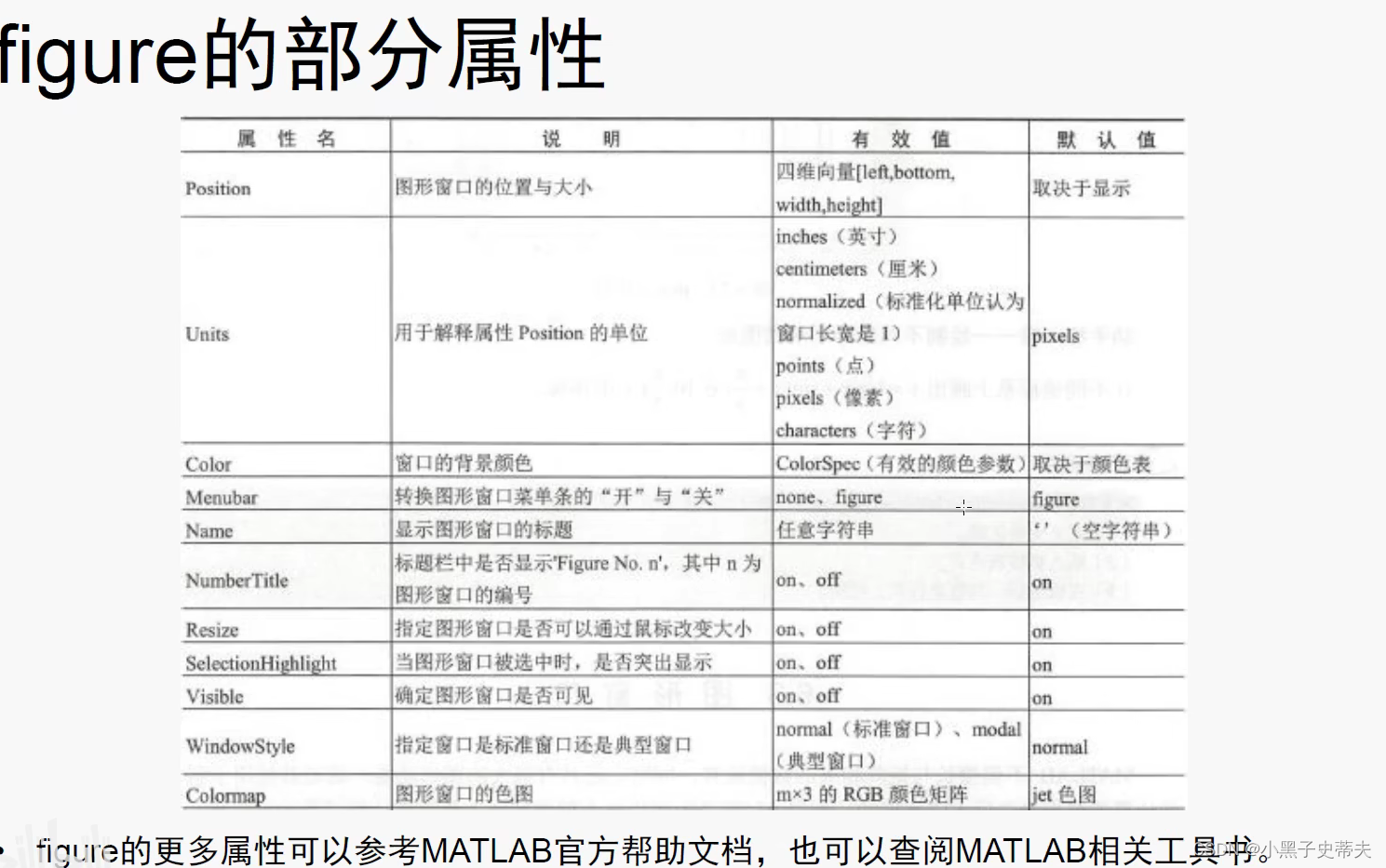

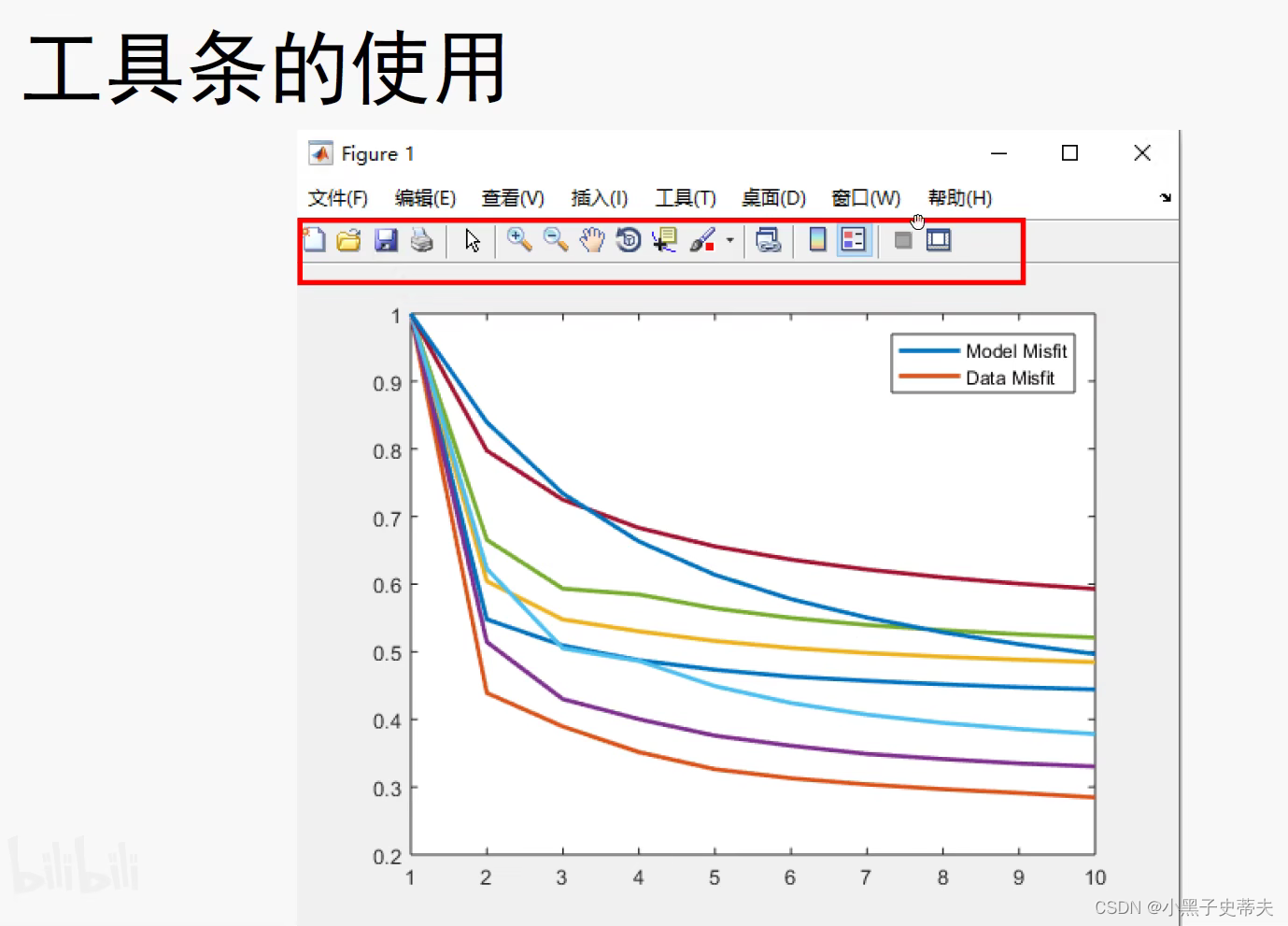
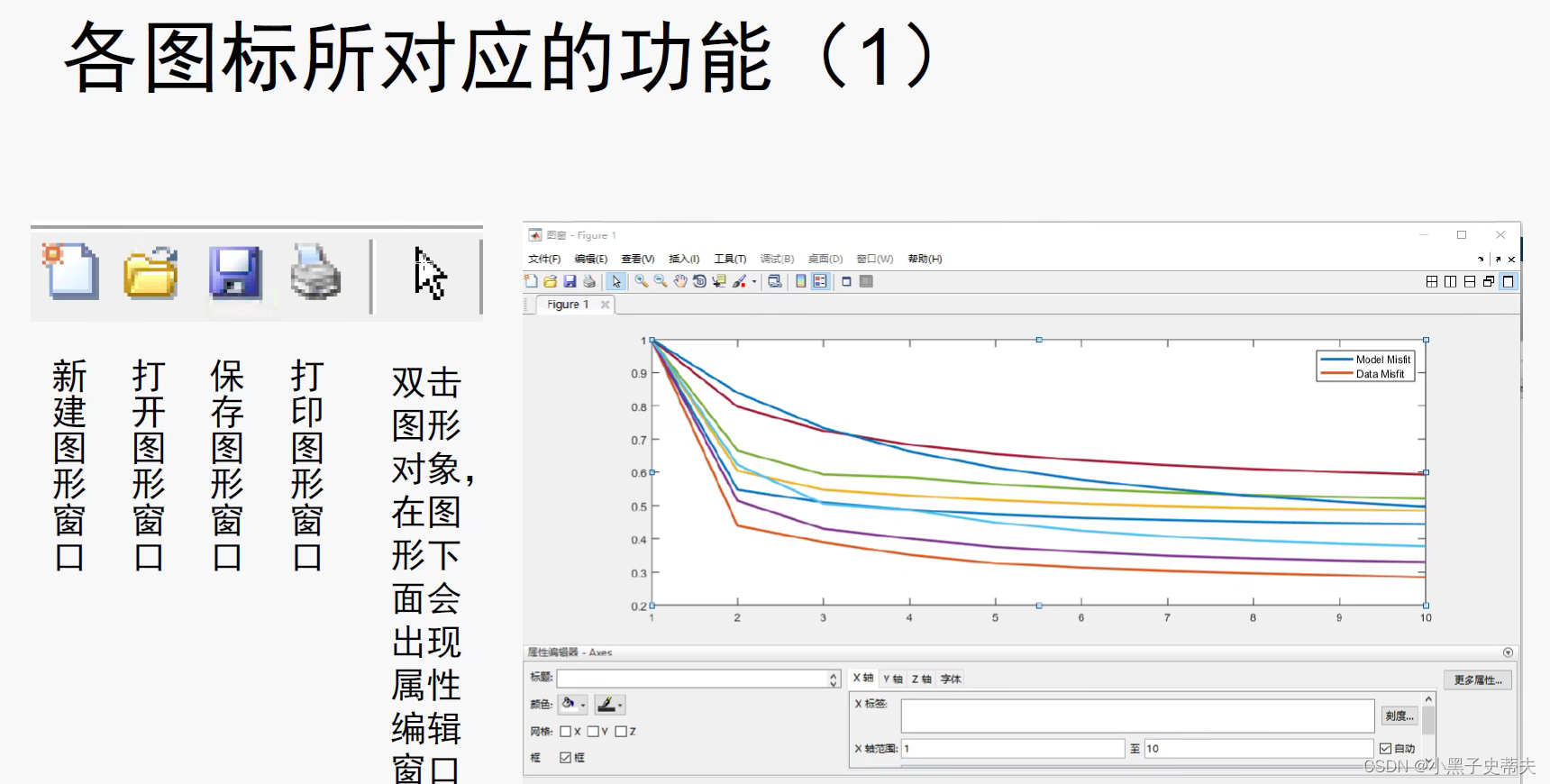
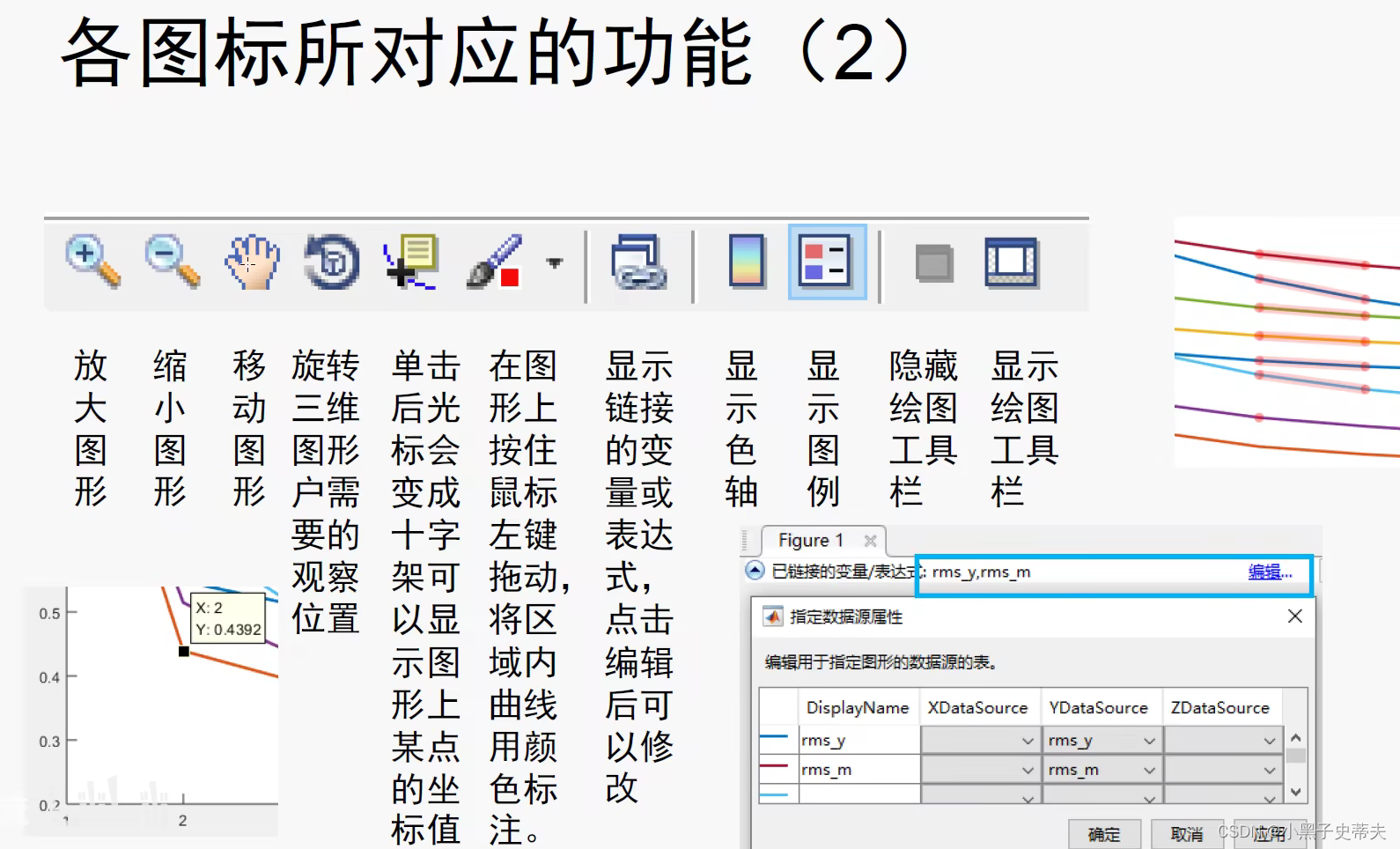
4.11 坐标系与坐标轴axis


4.12 图形注释

4.13 文本属性
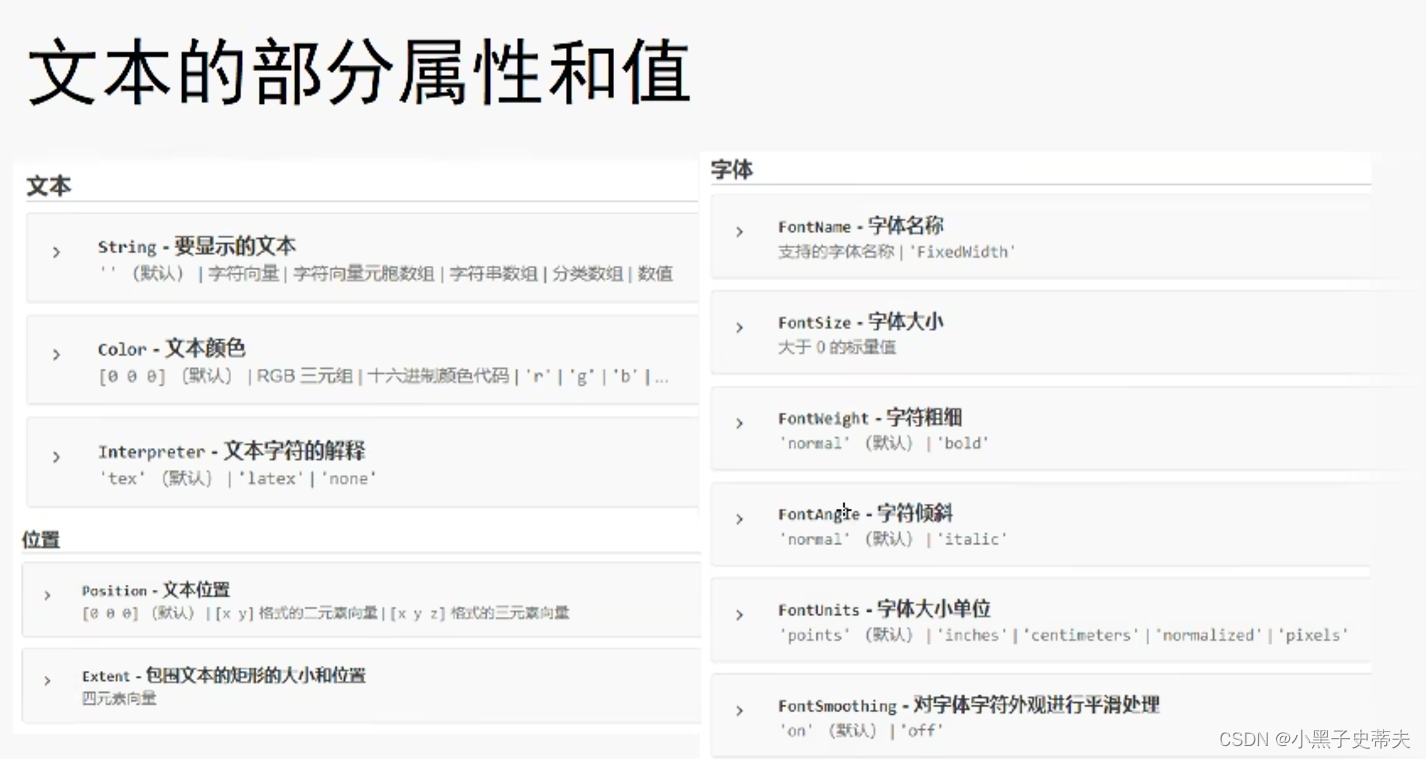
4.14 legend 添加图例

4.15 grid 坐标区网格线
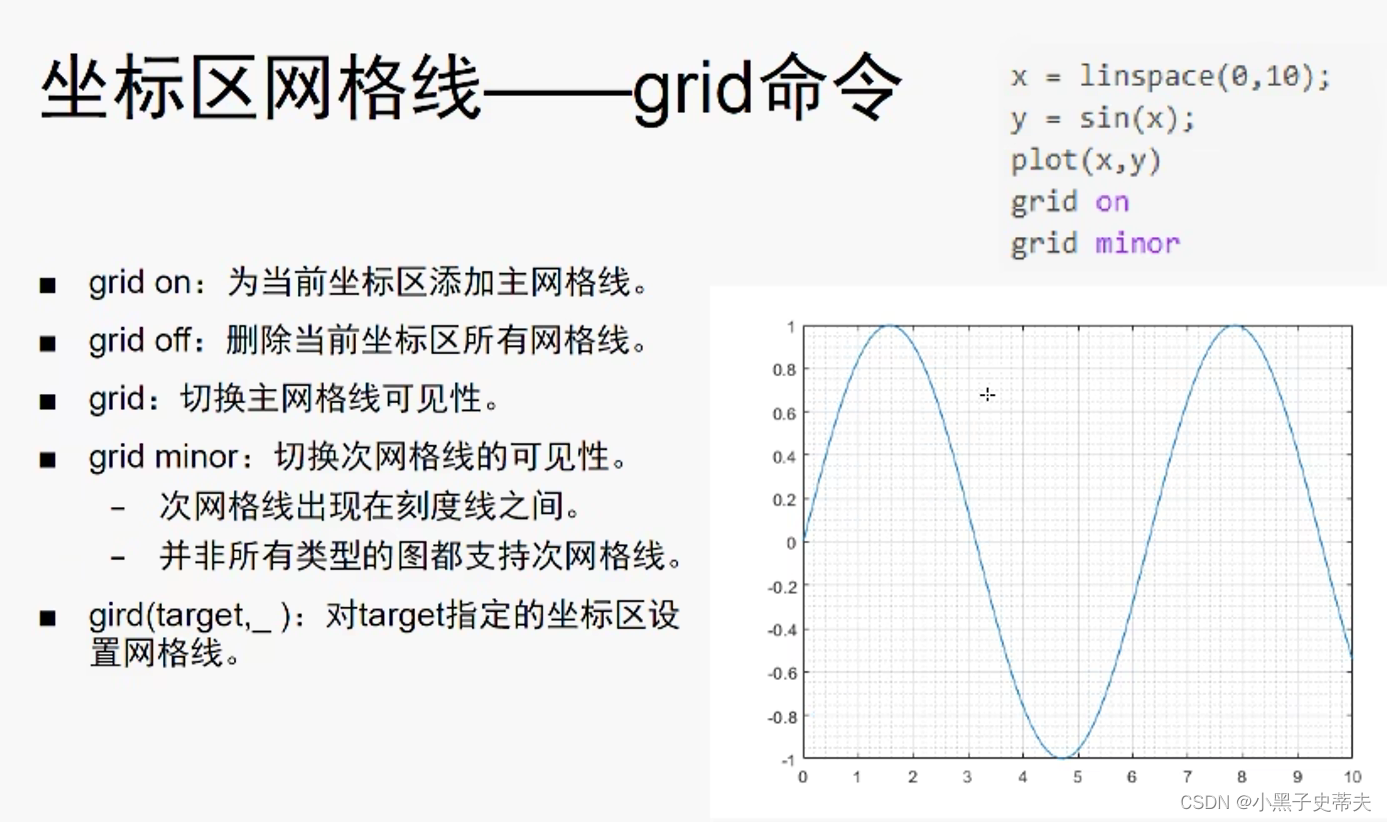
4.16 area 区域图
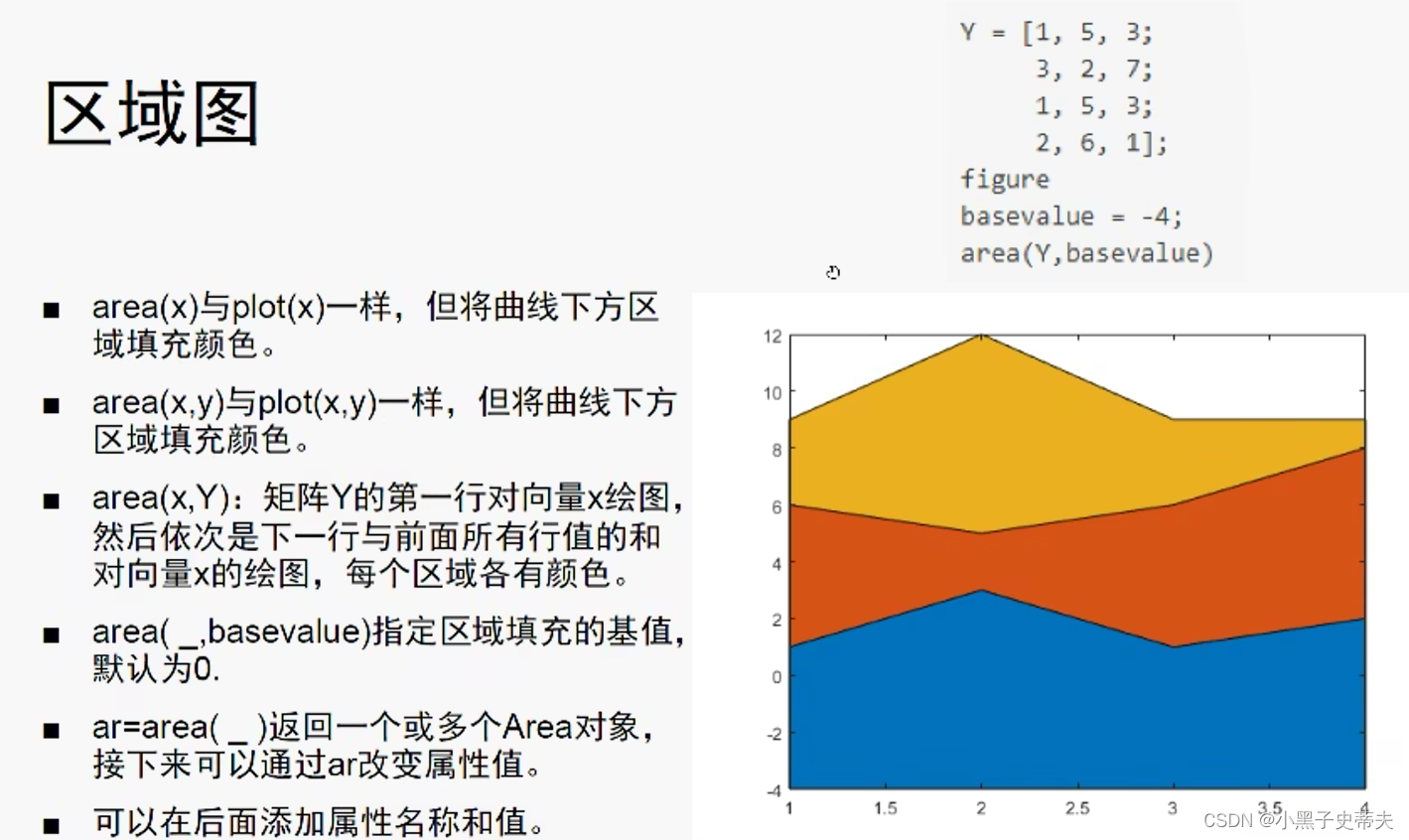
4.17 pie饼图 和 histogram直方图

4.18 errorbar 含误差条的线图
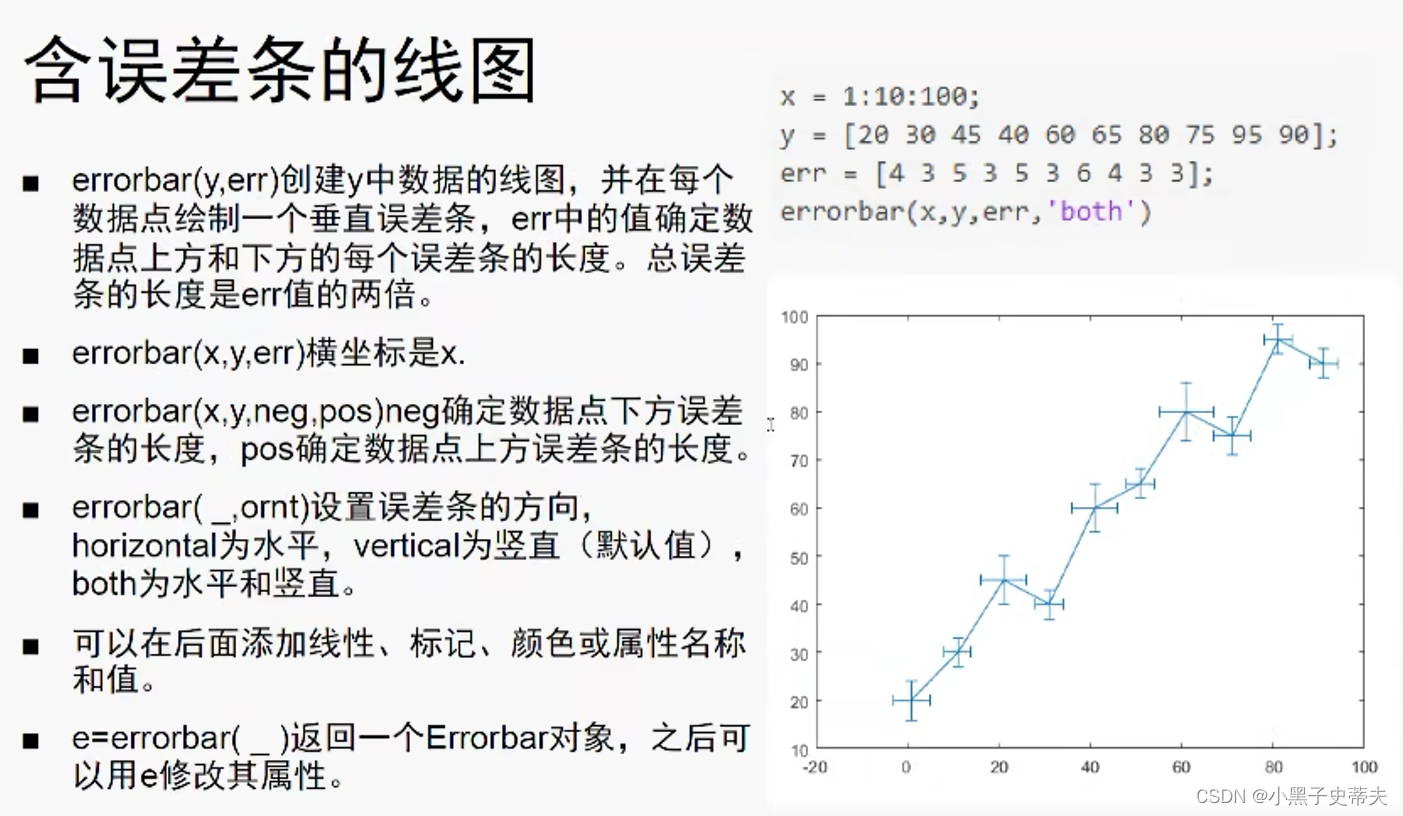
4.19 stem 针状图
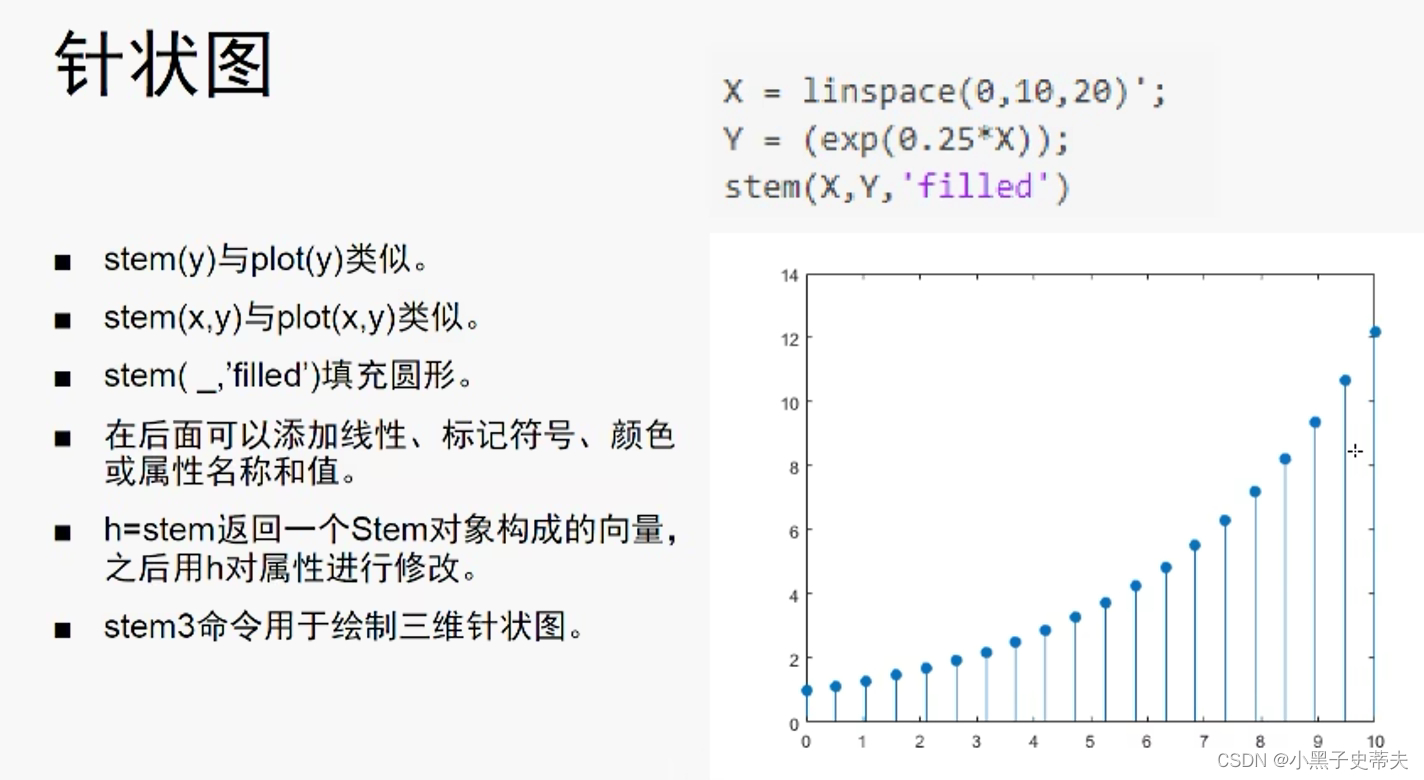
4.20 stairs 阶梯图
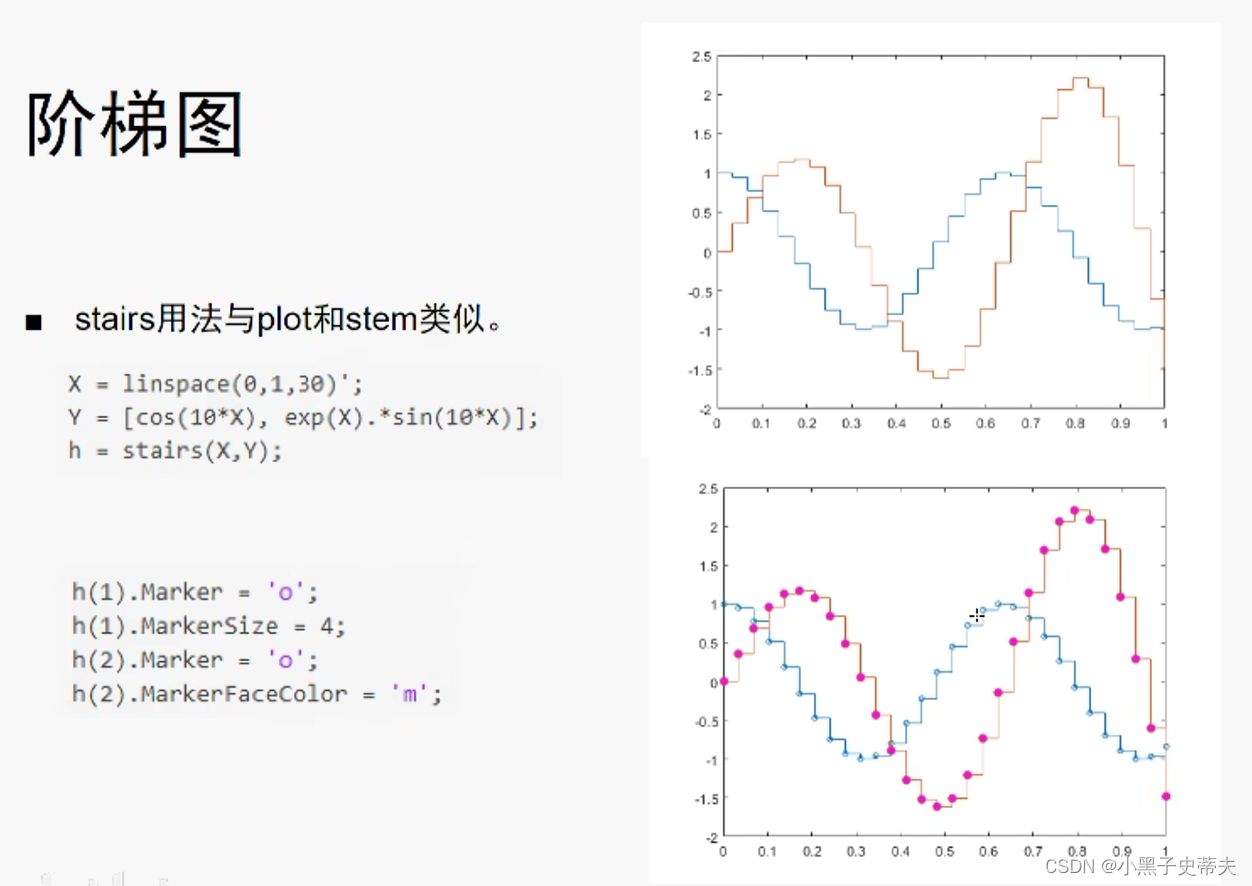
4.21 compass 罗盘图

4.22 quiver 箭头图
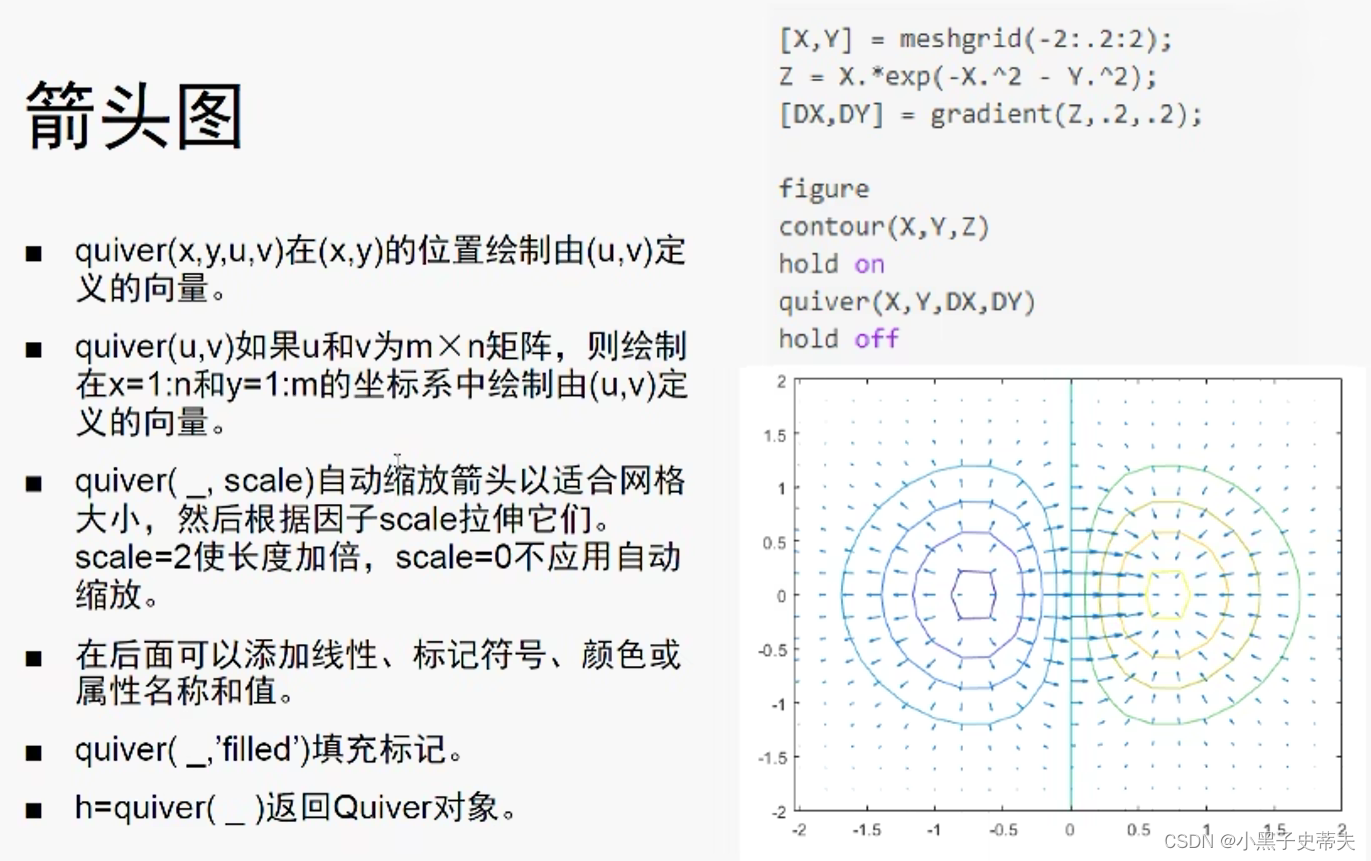
4.23 mesh 三维网格图
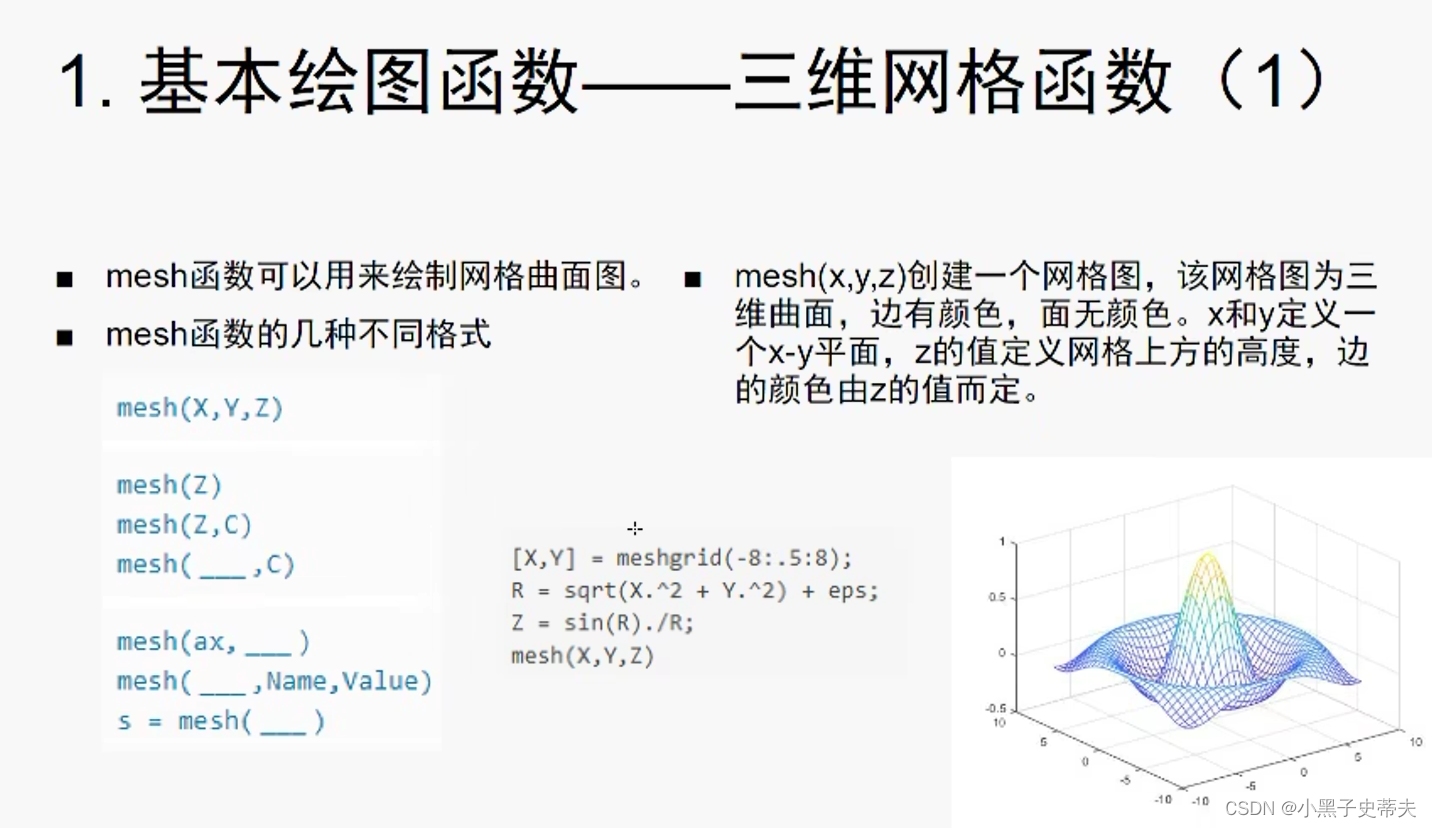


4.23.1 meshc 在网格图下展示等高线
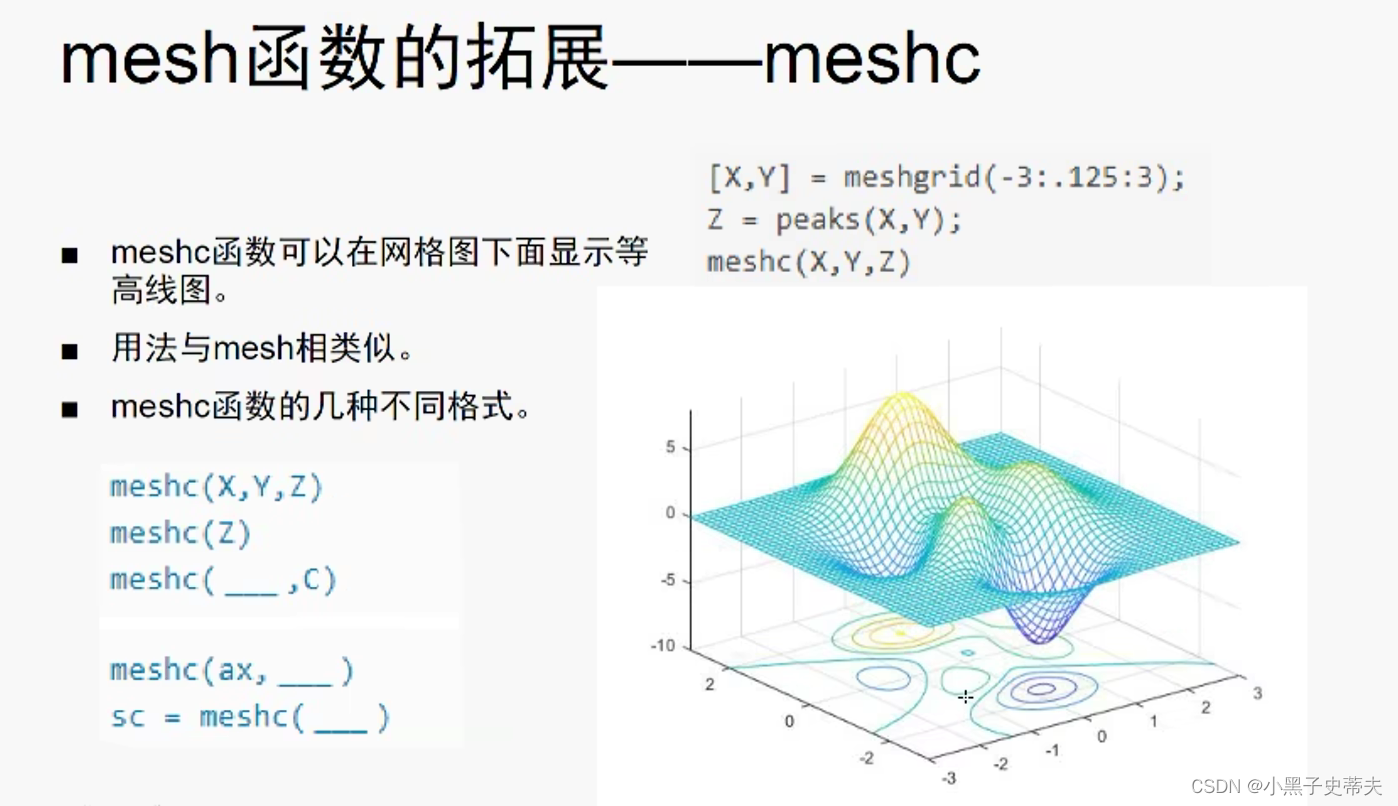
4.23.2 meshz 在网格图下展示帷幕
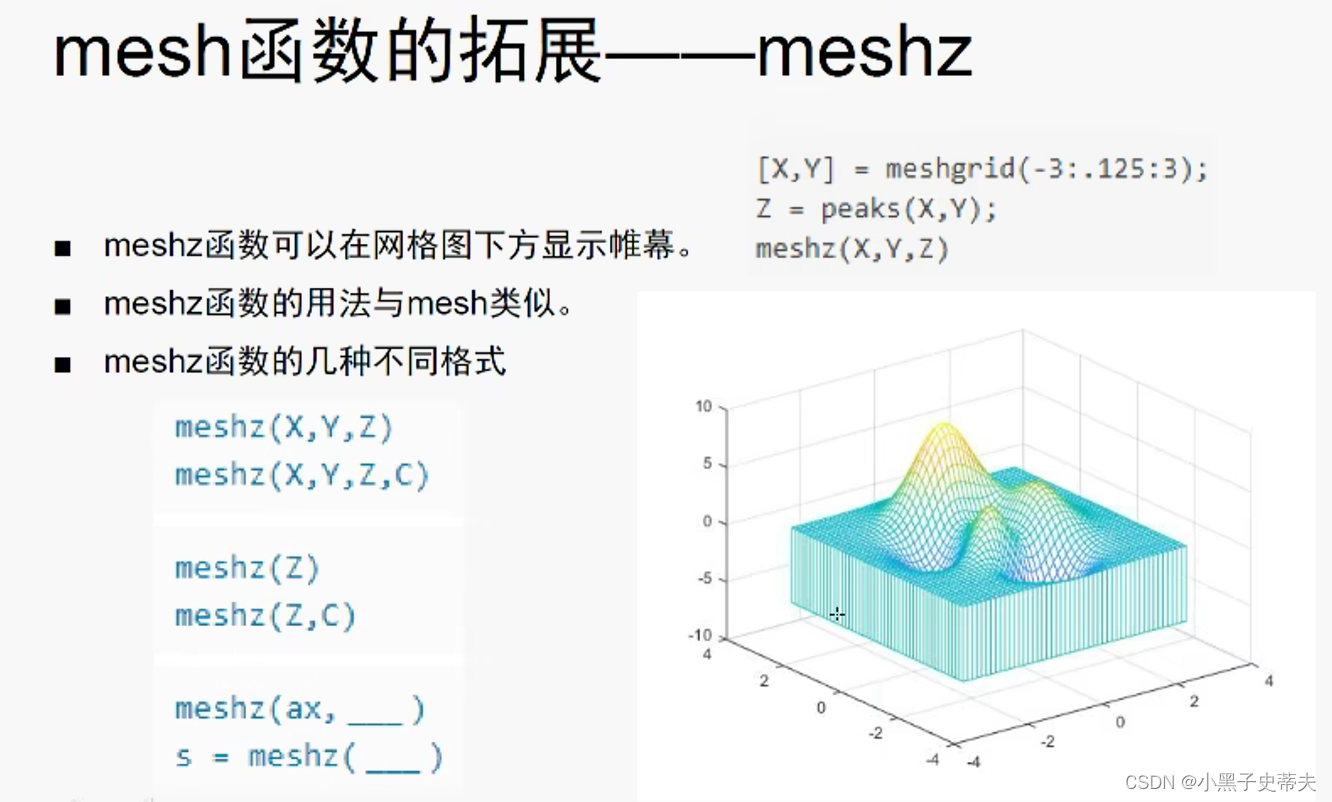
4.24 三维网格ezmesh 和 三维曲面surf

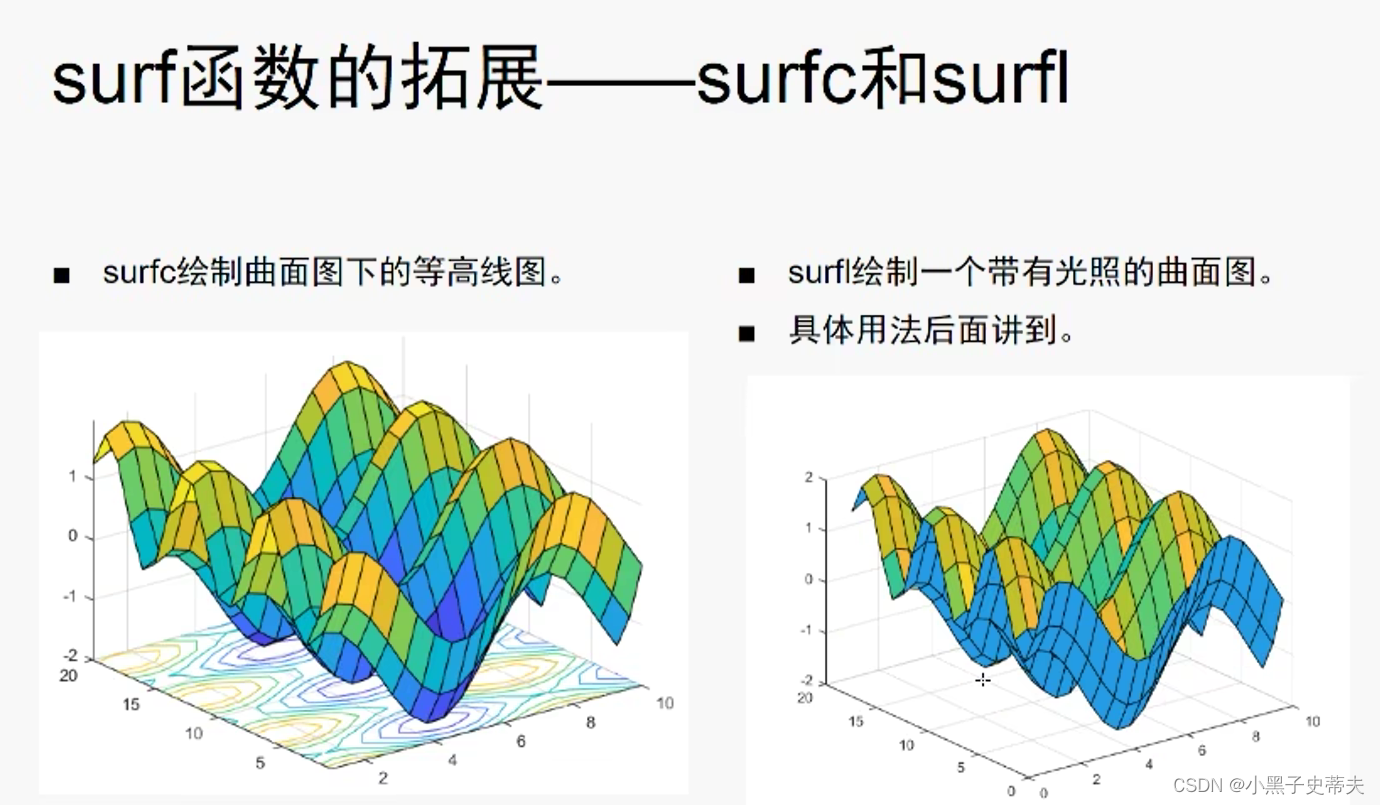

4.25 cylinder 柱面
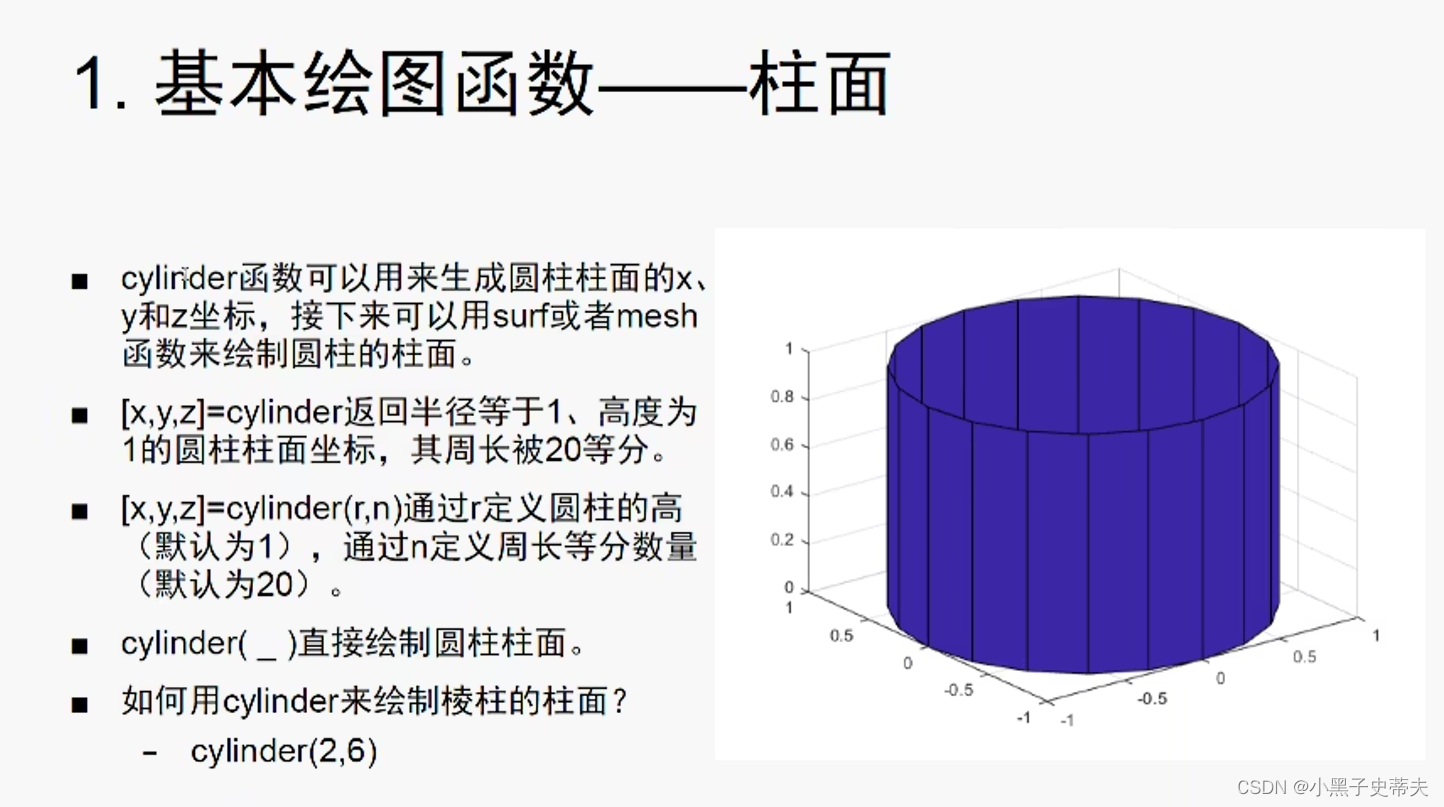
4.26 球面
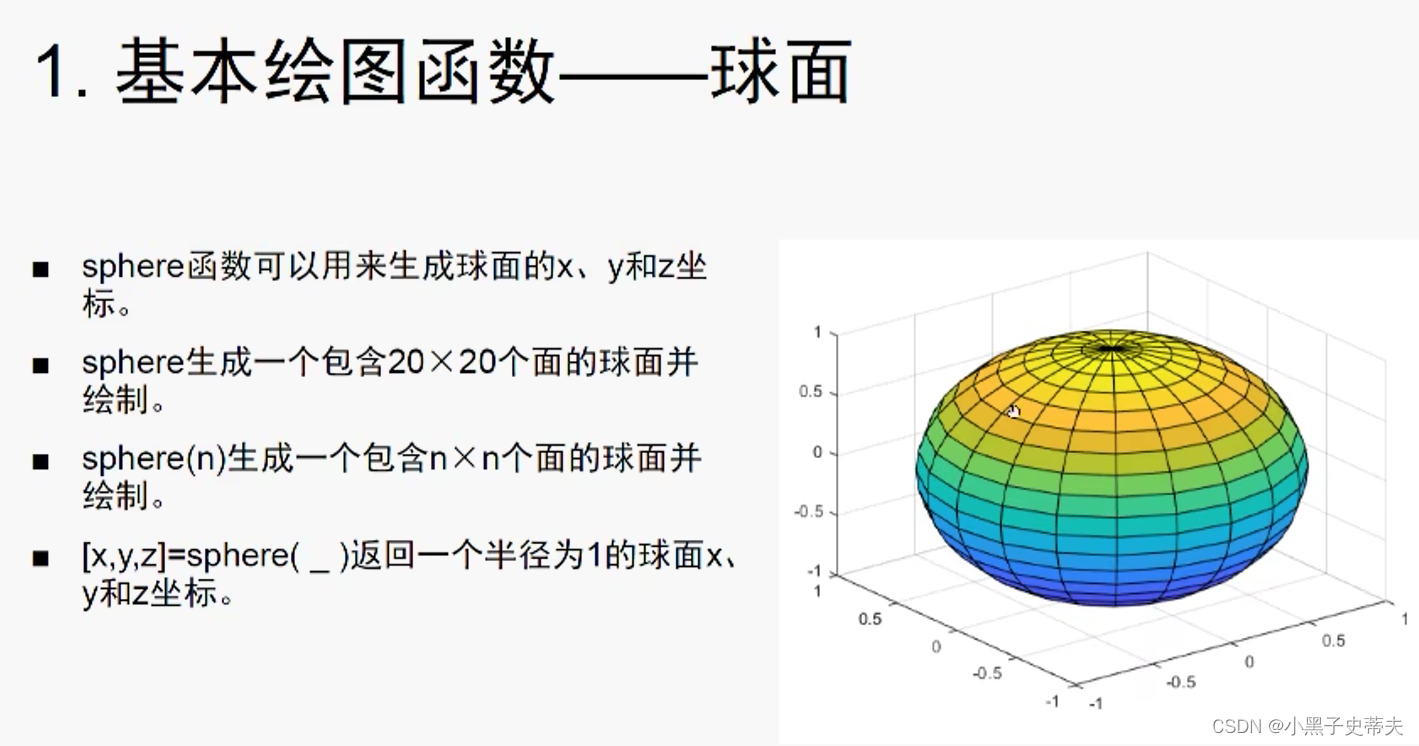
4.27 contour3 等高线图

4.27.1 contourc等高线矩阵的计算

4.27.2 为等高线添加标签
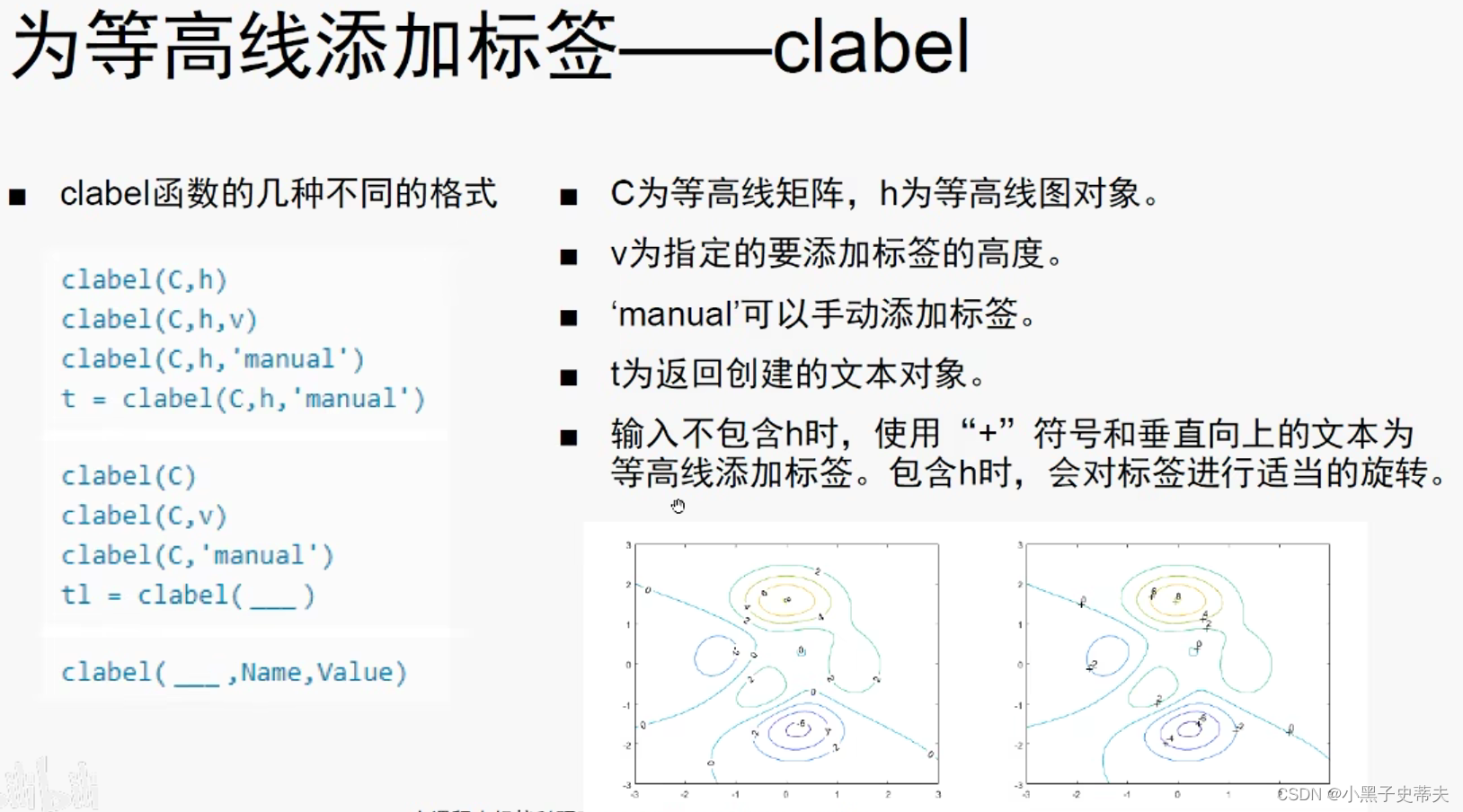
4.28 三维图形的修饰处理
4.28.1 view 视角处理

4.28.2 brighten、caxis、colorbar 、shading、colormap颜色处理

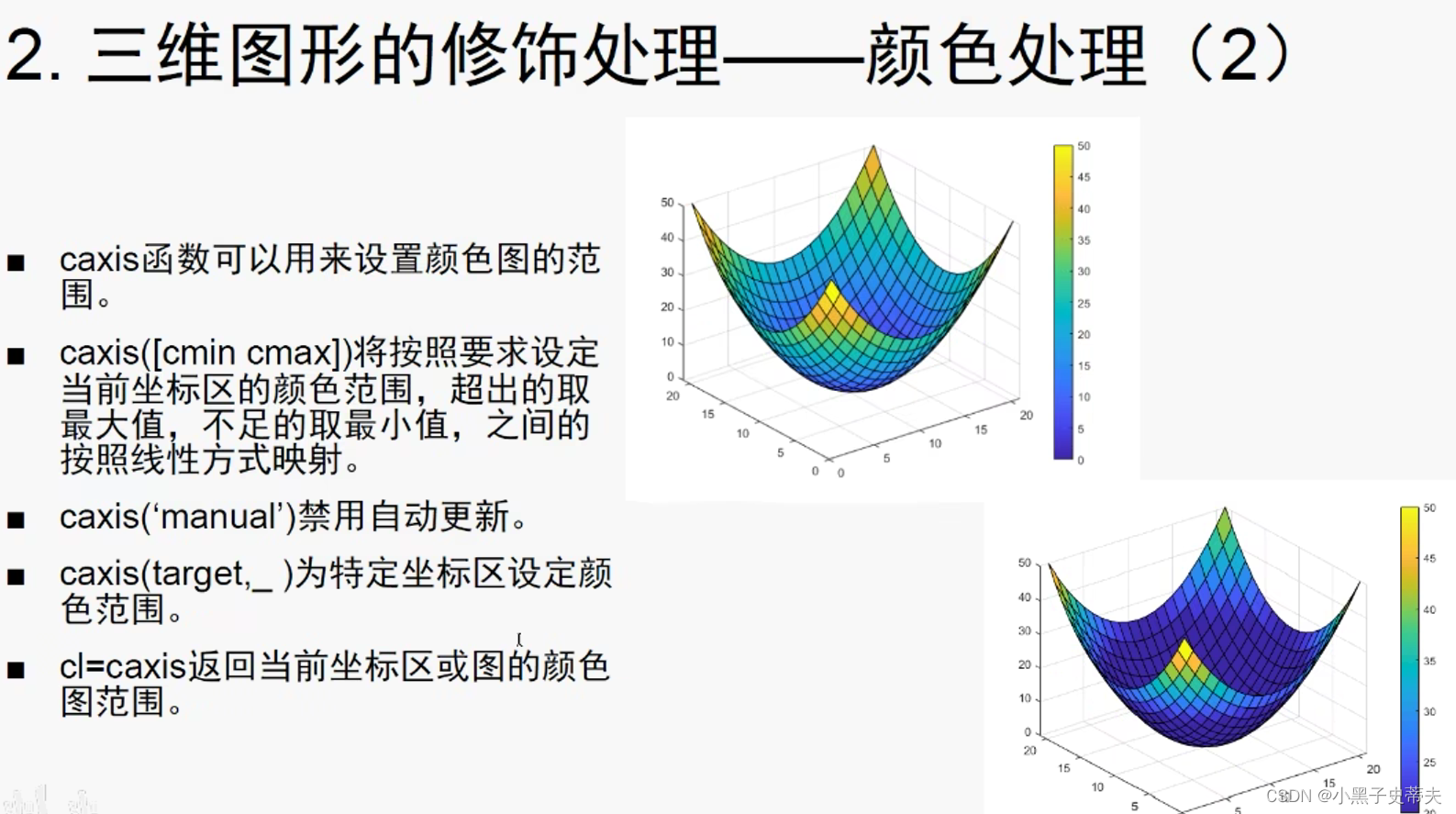

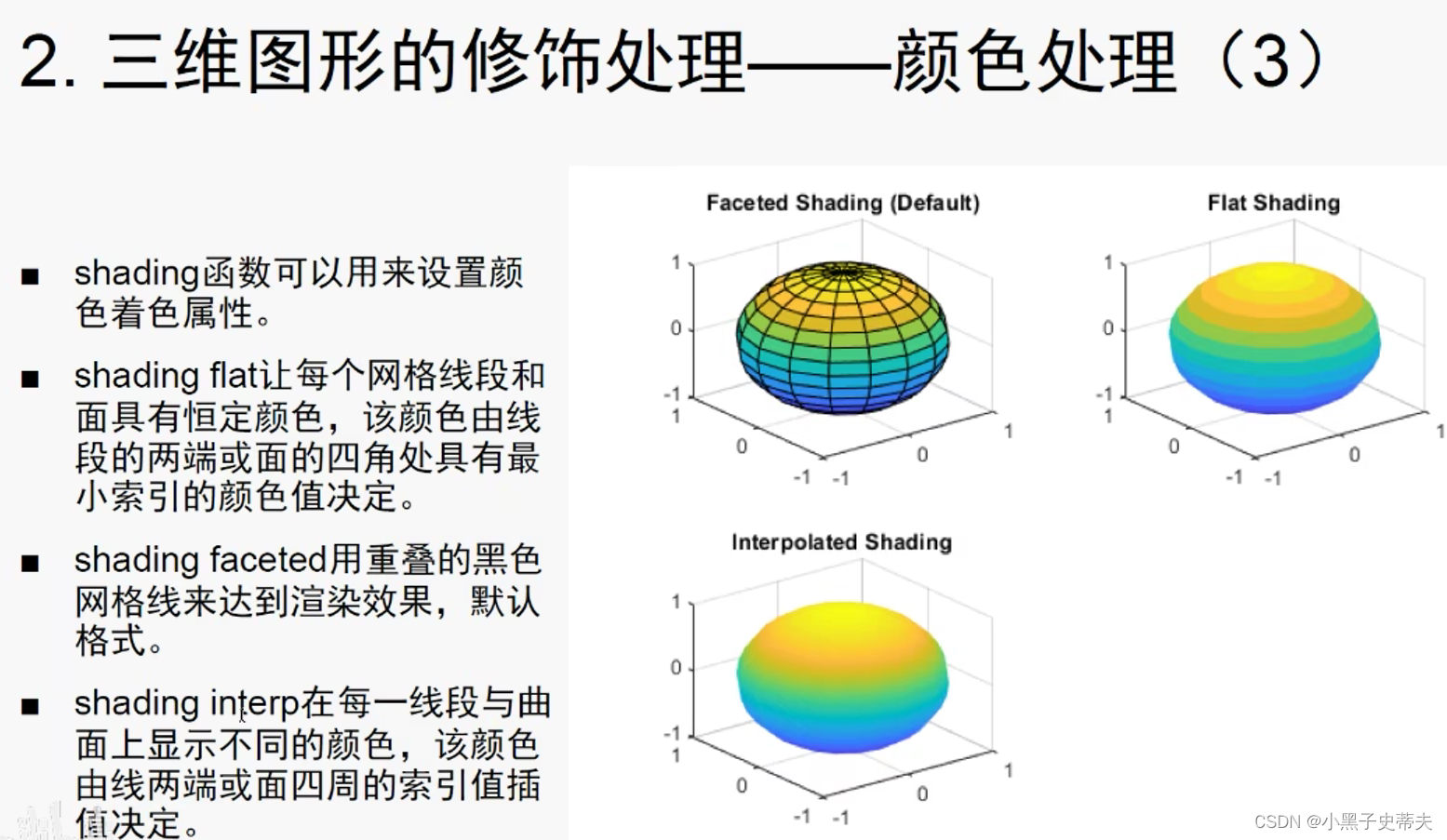
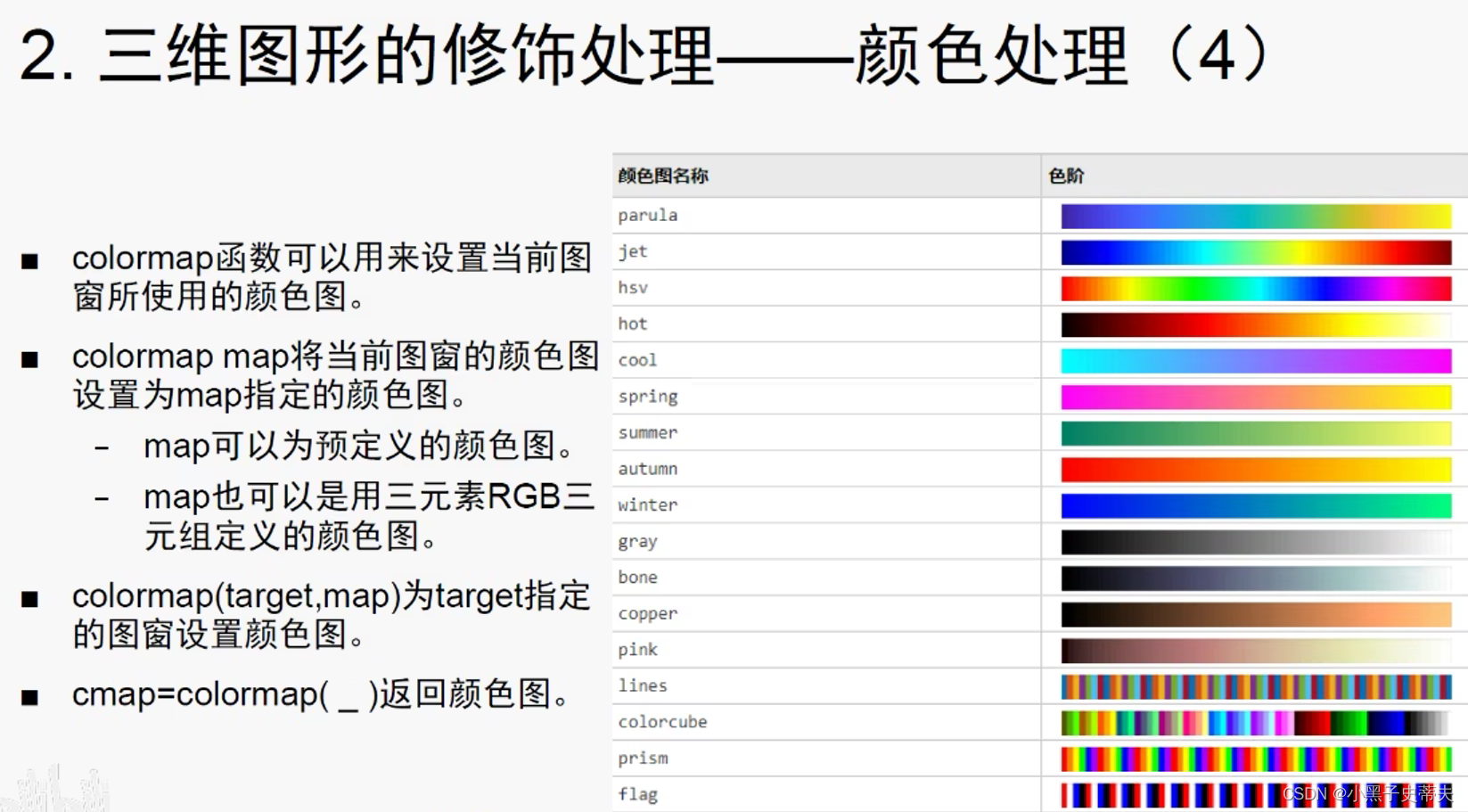
4.28.3 光照处理surfl 和 light


5. matlab导入数据
导入范围:
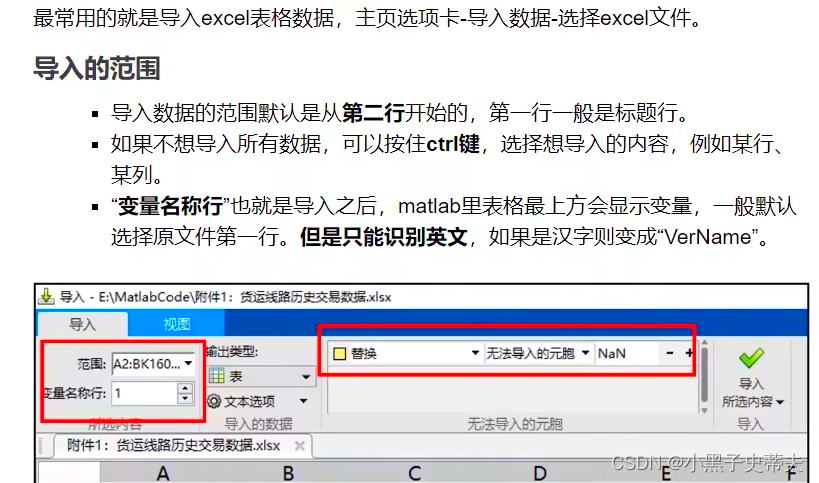
例:
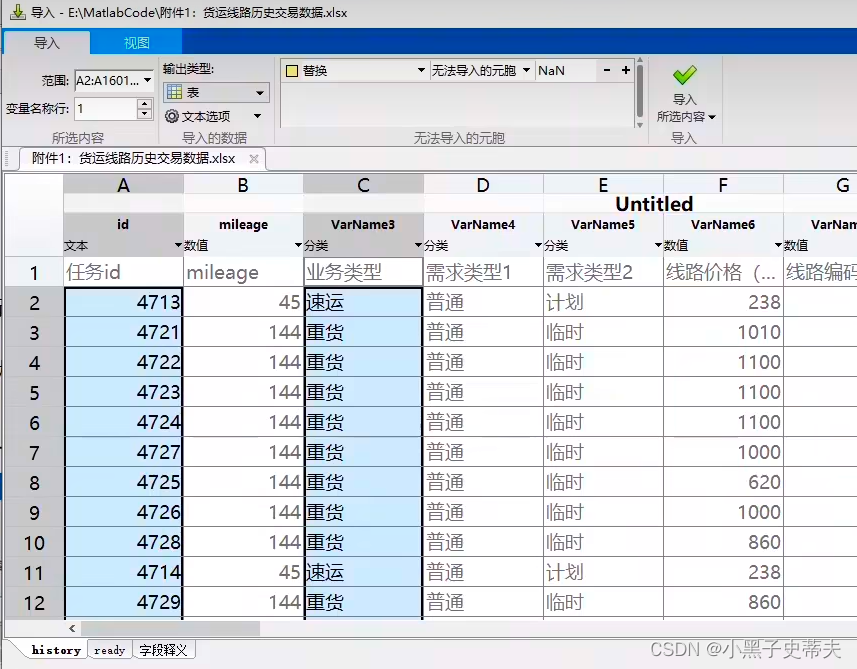
导入类型:
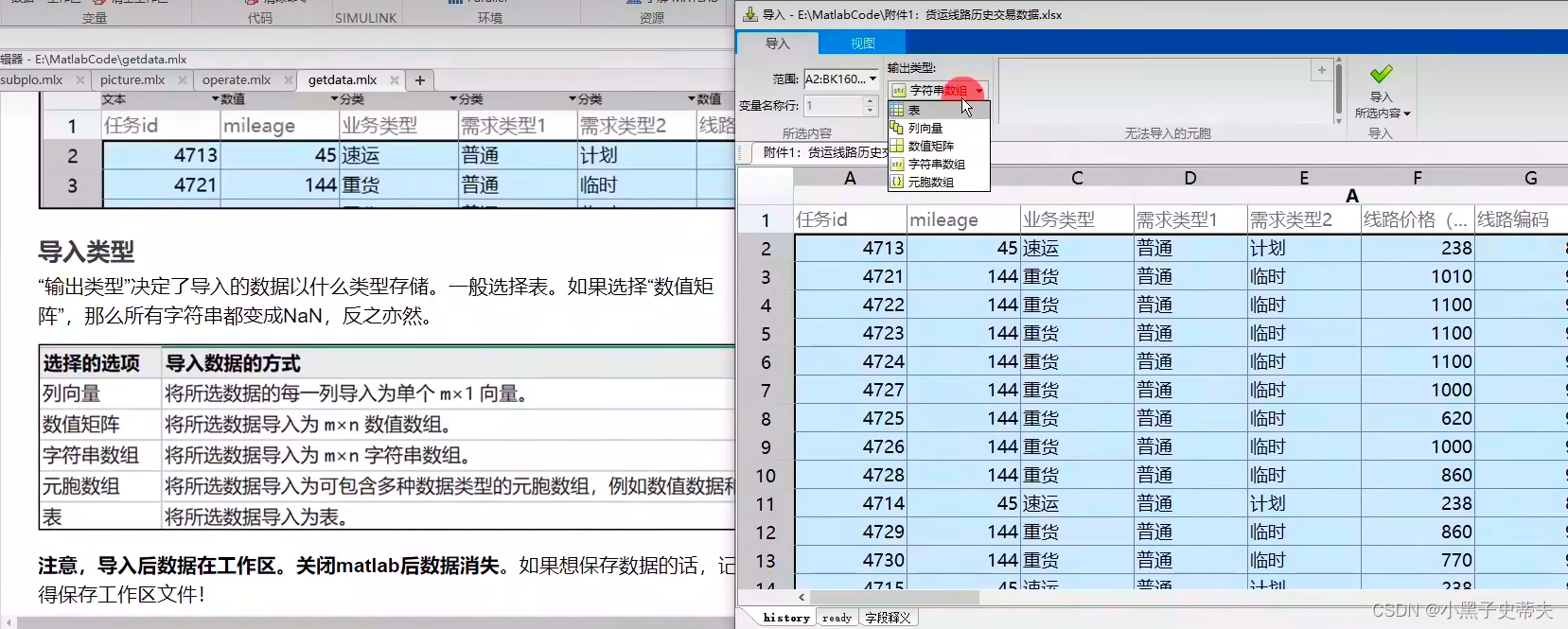
处理无法导入的数据:
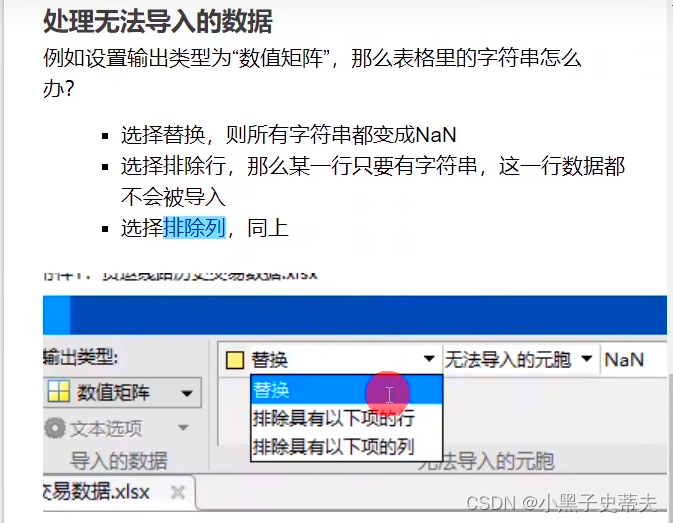
6. matlab处理缺失值和异常值
清理缺失数
实时编辑器,选择任务>清理缺失数据首先,先写一组包含缺失值和异常值的例子
x = 1:100;%构造一个数组,元素为1,2,3,.......100
%randn( 1,100)意味着生成一个1行1日e列的矩阵
%矩阵元素的均值为e,方差o^2 = 1,且是正态分布的随机数data = randn(1,100) ;
data(28:20:80)= NaN;
%设置第2e,40,6e,80个元素为缺失值
%data的值都是在e附近的,设置4个异常值
data(10) = -50;
data(40) = 45;
data(7e) = -40;
data(9e) = 5
eplot(x,data)
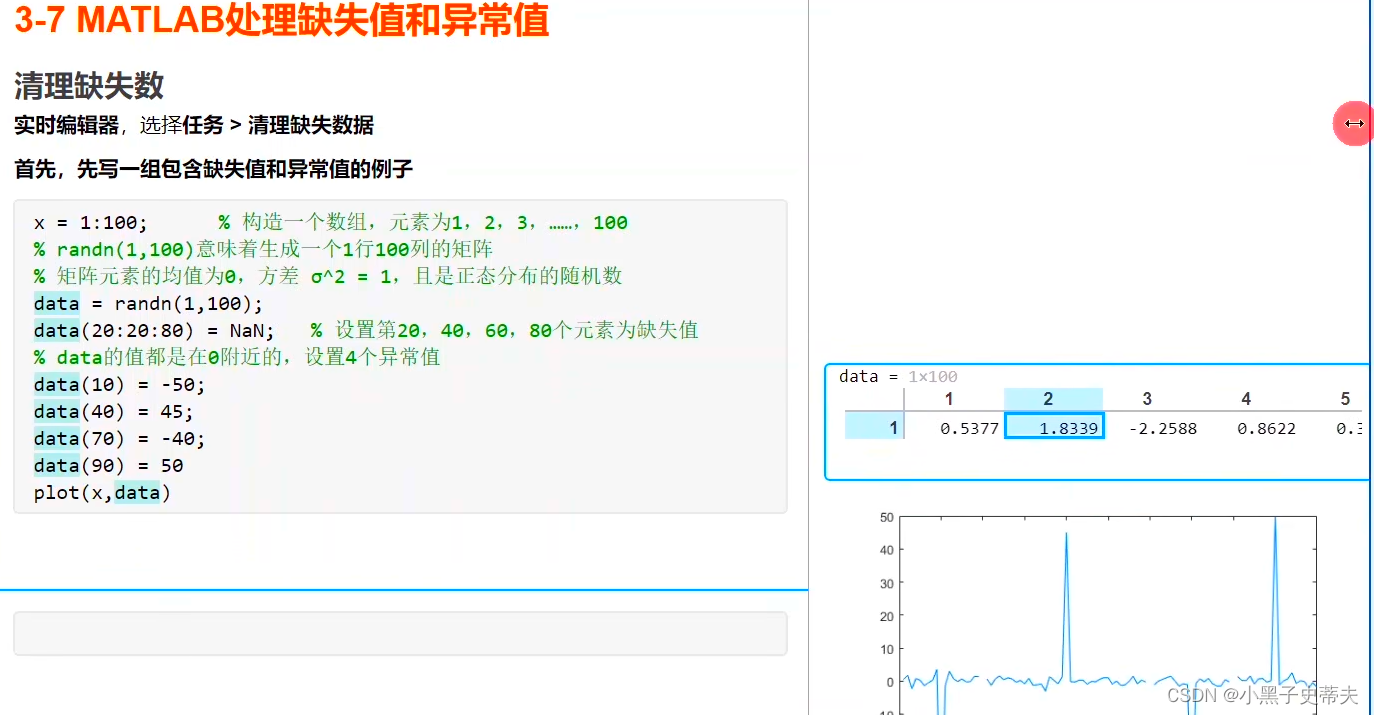
当遇到这种情况怎么办?
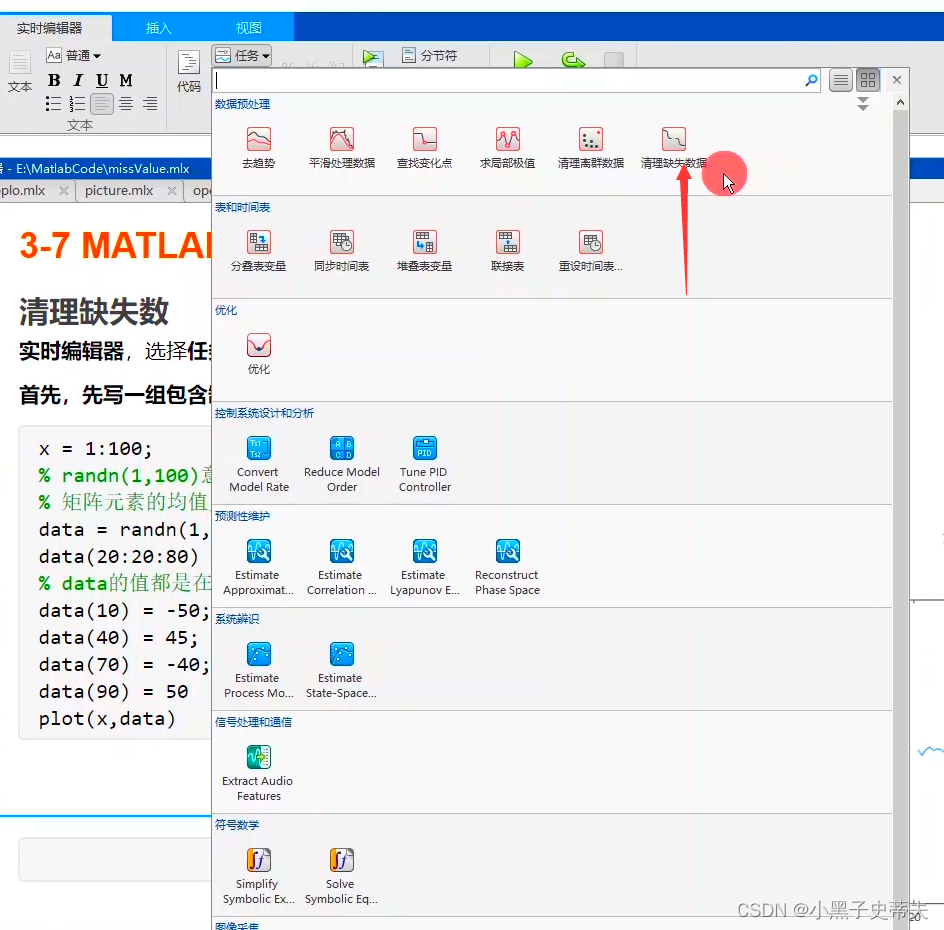
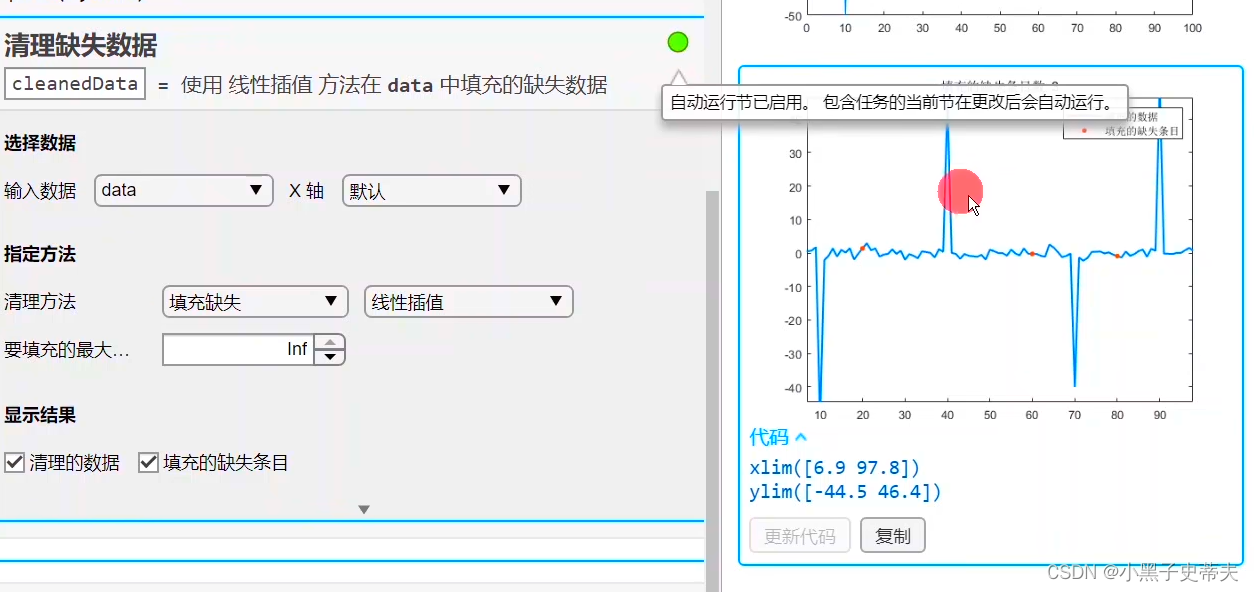
- 补上的差值就是红点
清理离群数据:
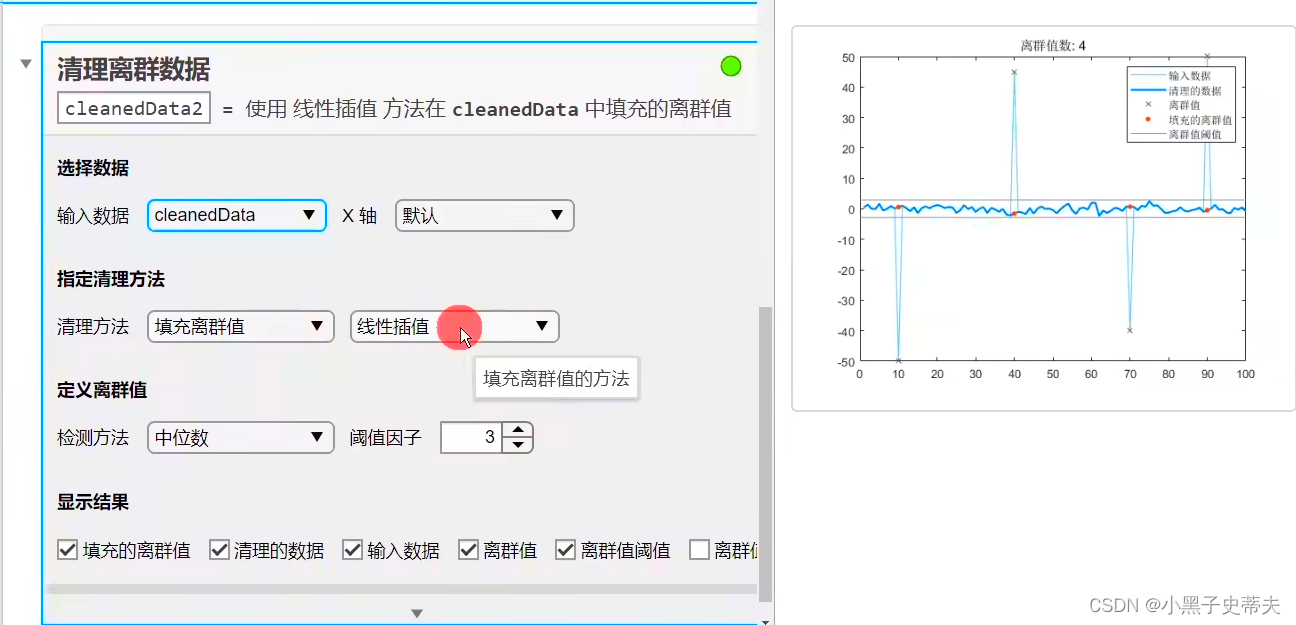
- 对于异常值会给个❌,再补成正常数值
7. 数模常用作图代码解析
7.1 二维曲线

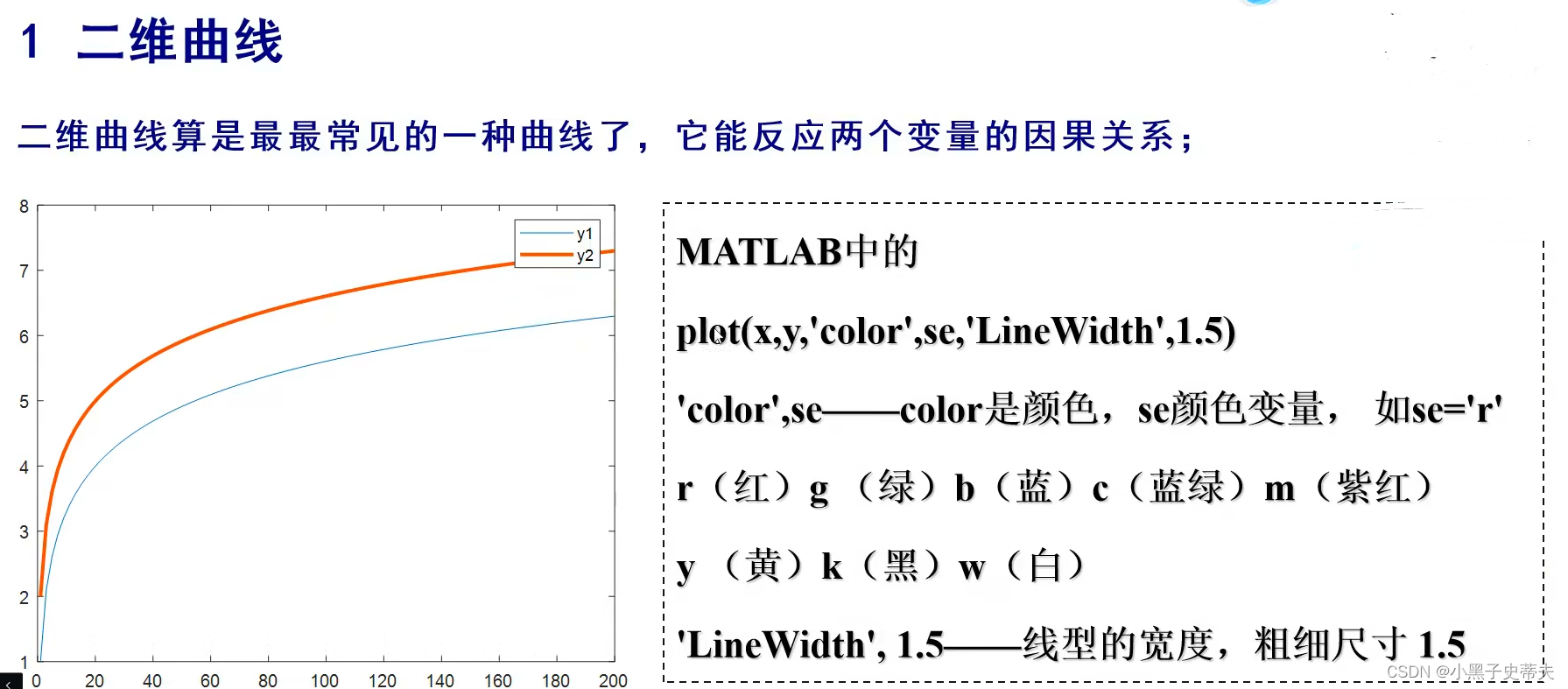
7.2 二维散点图

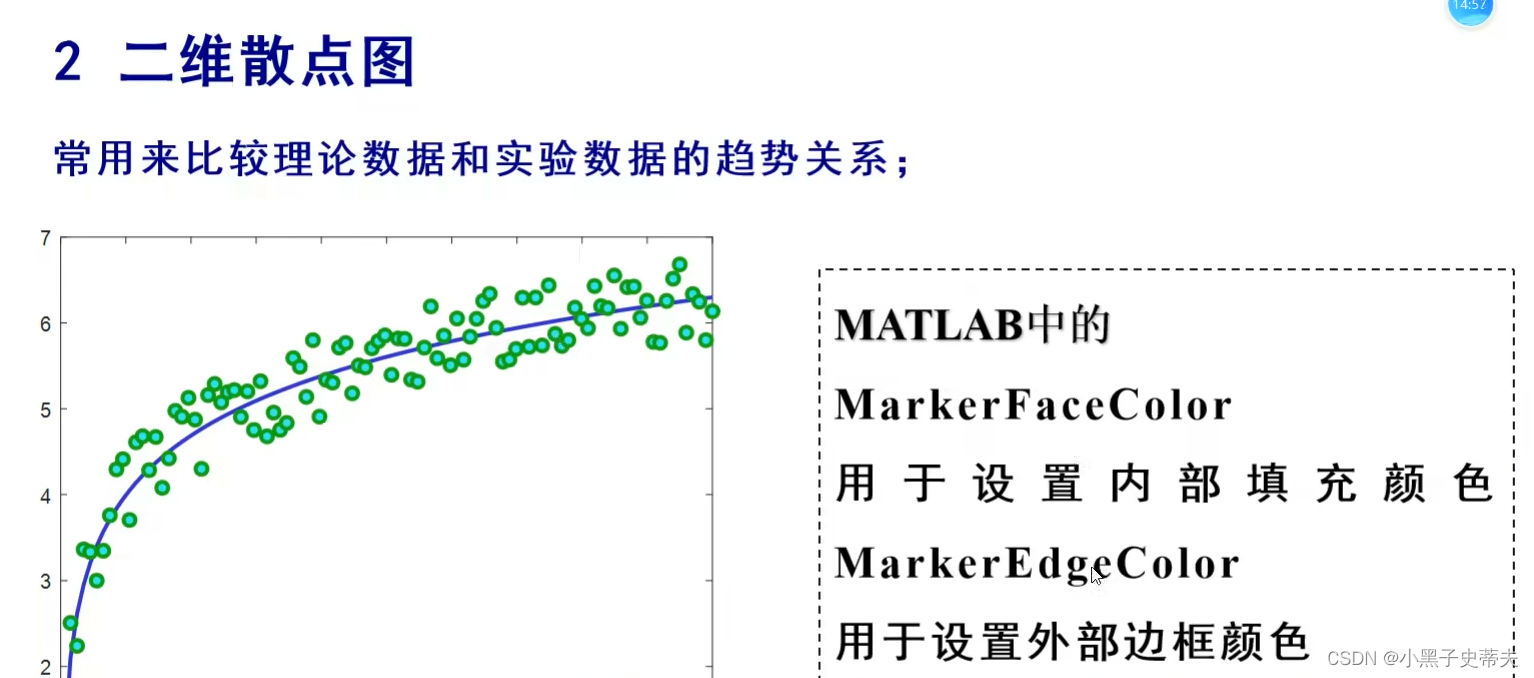
7.3 scatter 二维渐变图

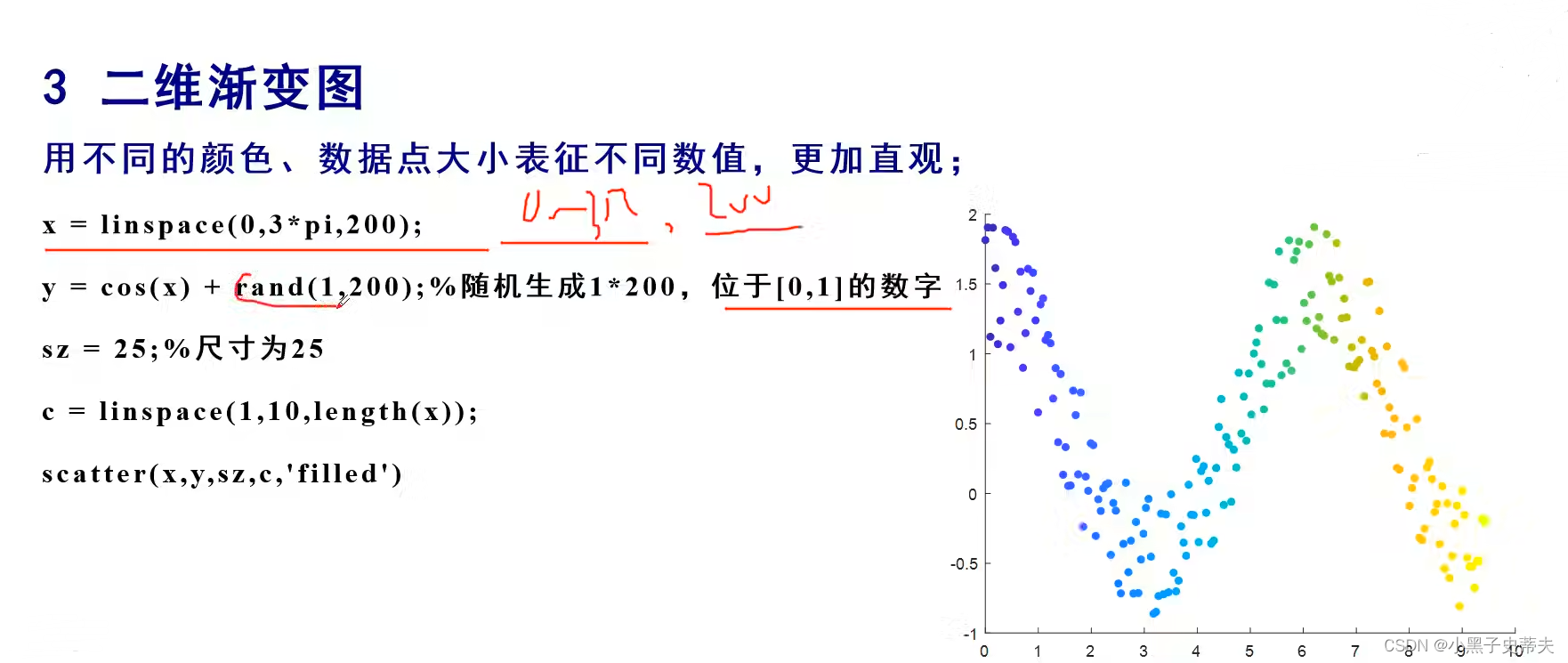

7.4 条形图
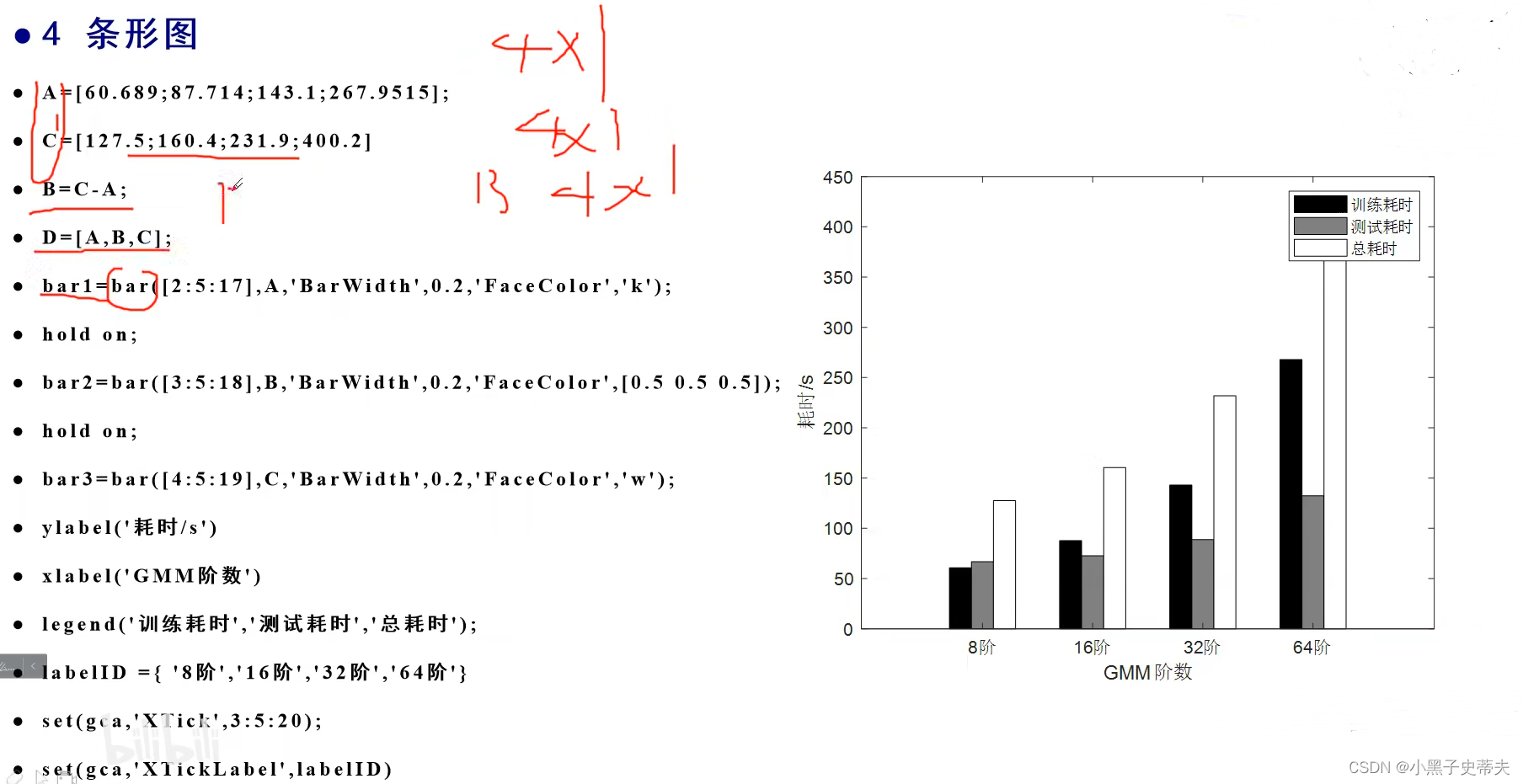
7.5 fill 填充图
填充图一般求多个函数交界的阴影部分
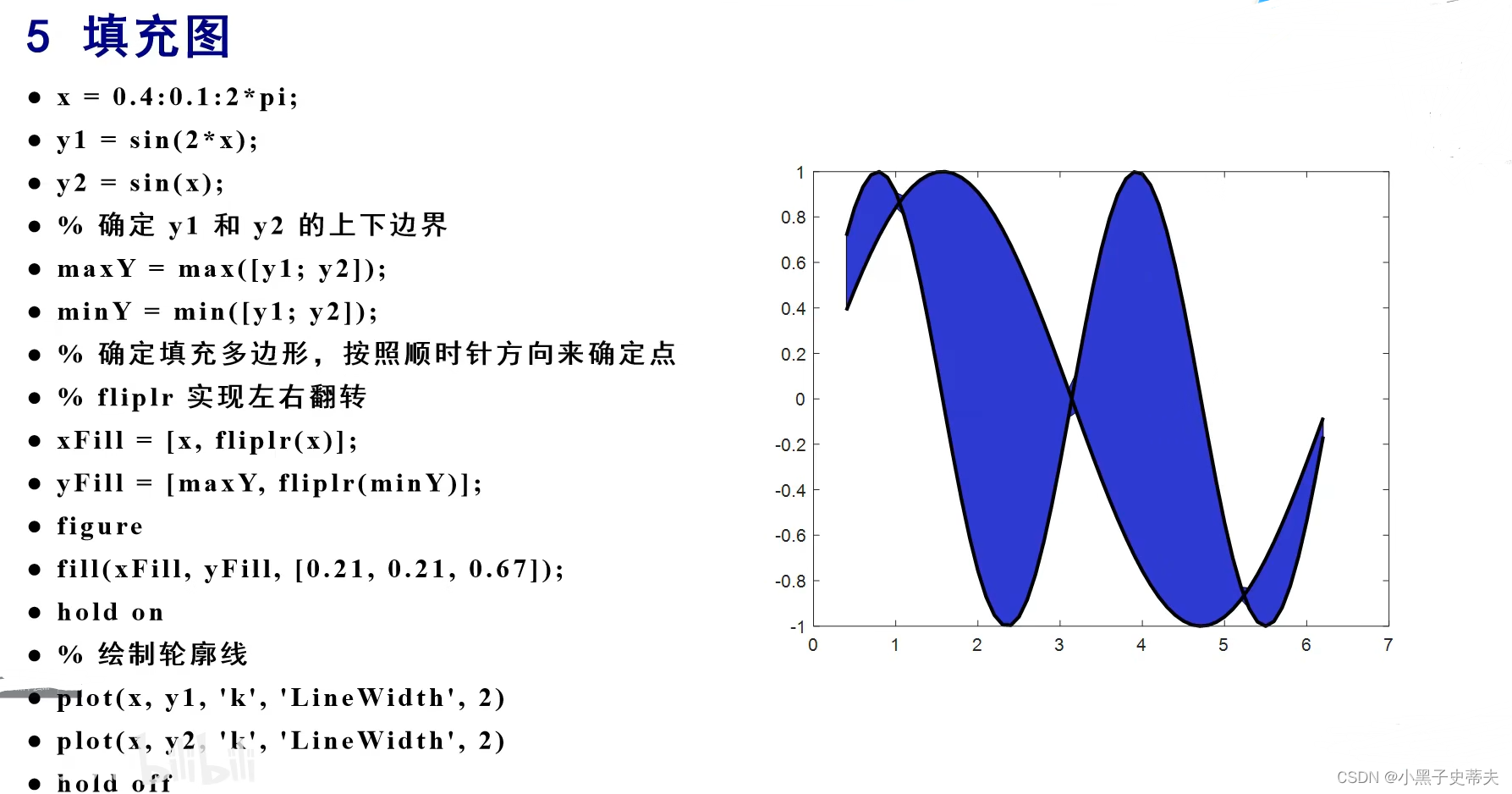
7.6 多Y轴图
多Y轴图适用于量级不一致的同组数据又需要展示的情况下
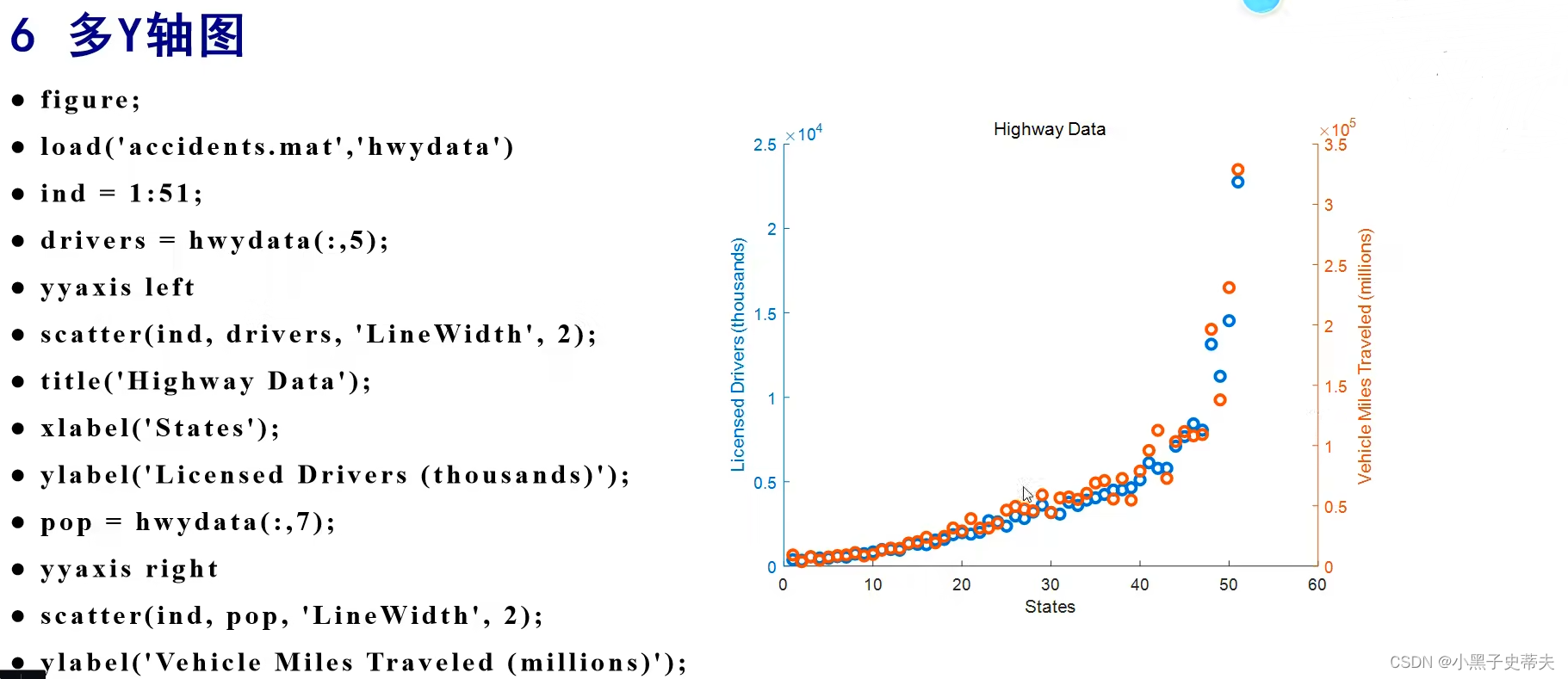
7.7 streamline 与 quiver 二维场图
场图可以直观地显示一些流体的动态情况,比如排水的流动、云的流动
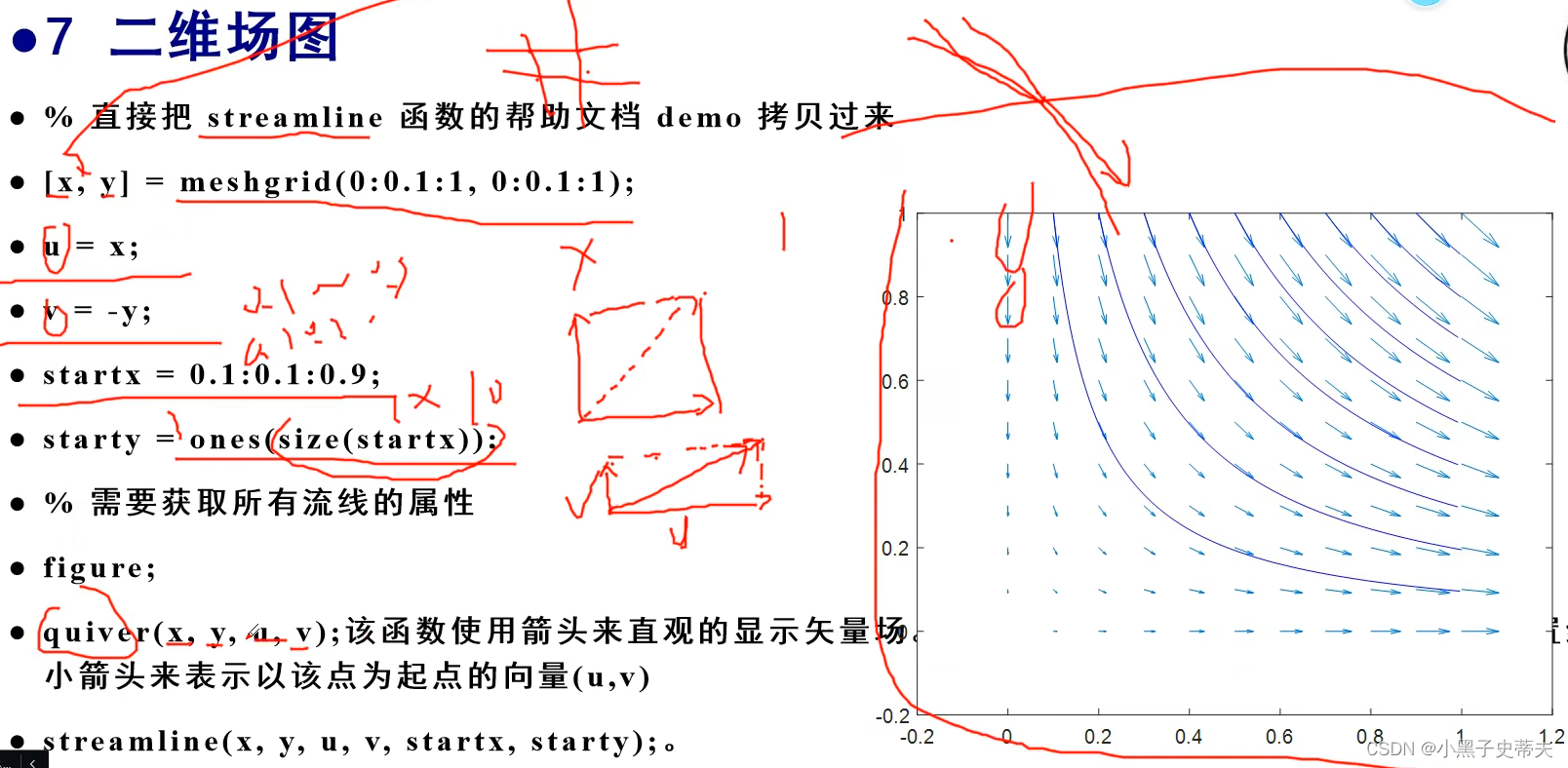
7.8 三维散点图
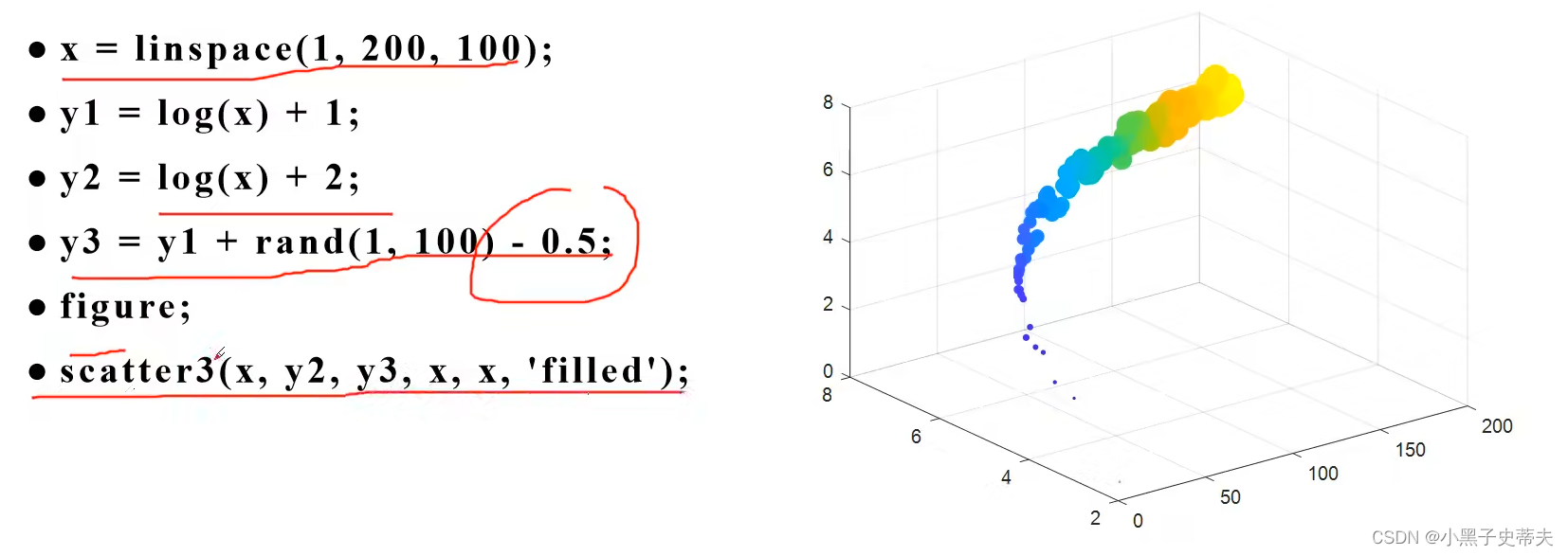
7.9 surf 与 colormap 三维伪彩图
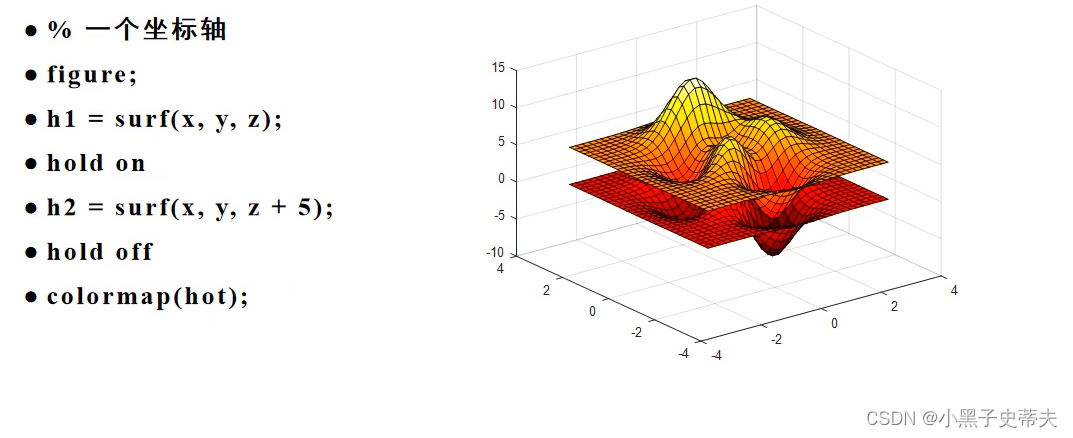
7.10 shading interp 裁剪伪彩图
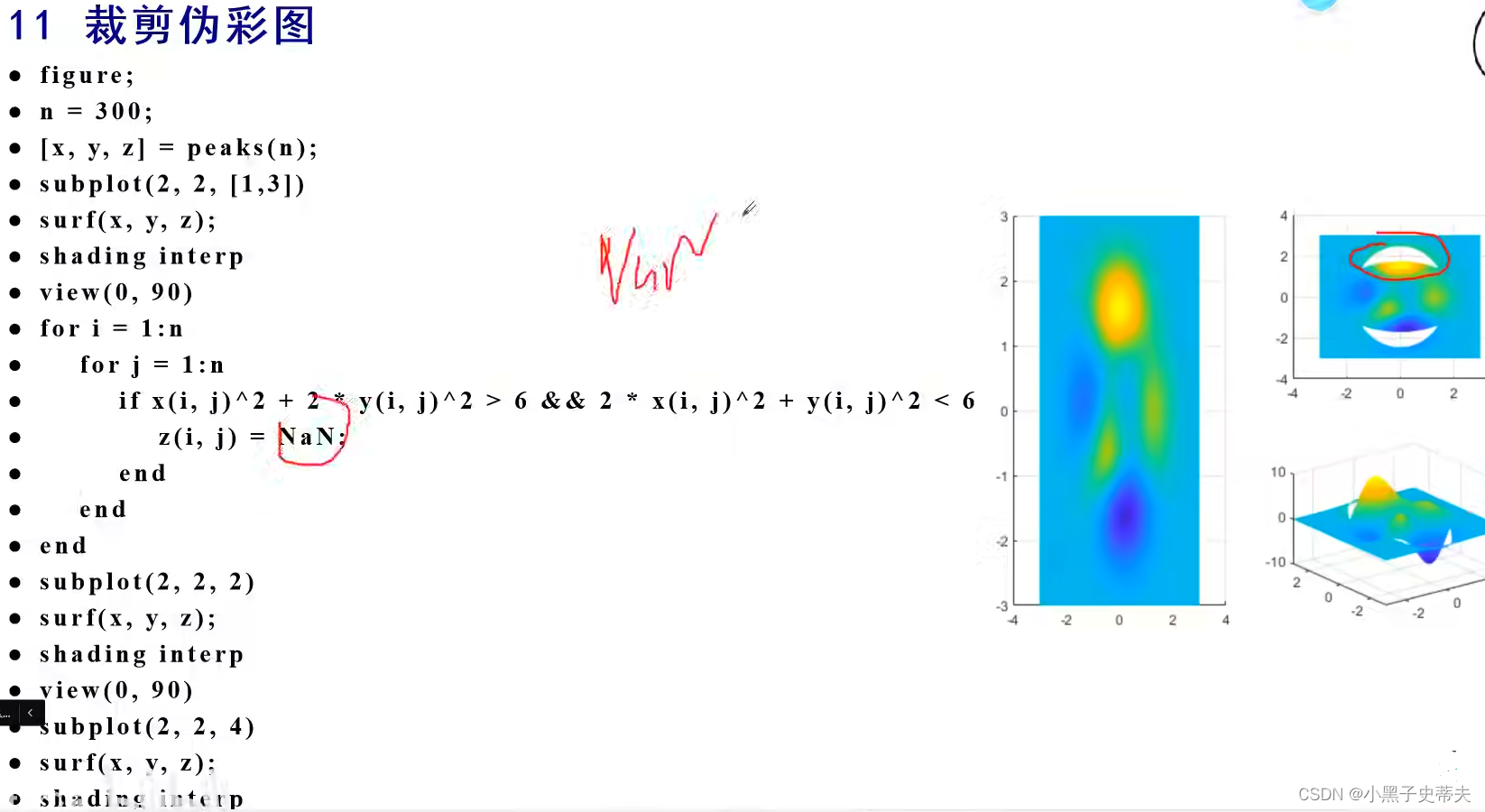
7.11 contour 等高线图
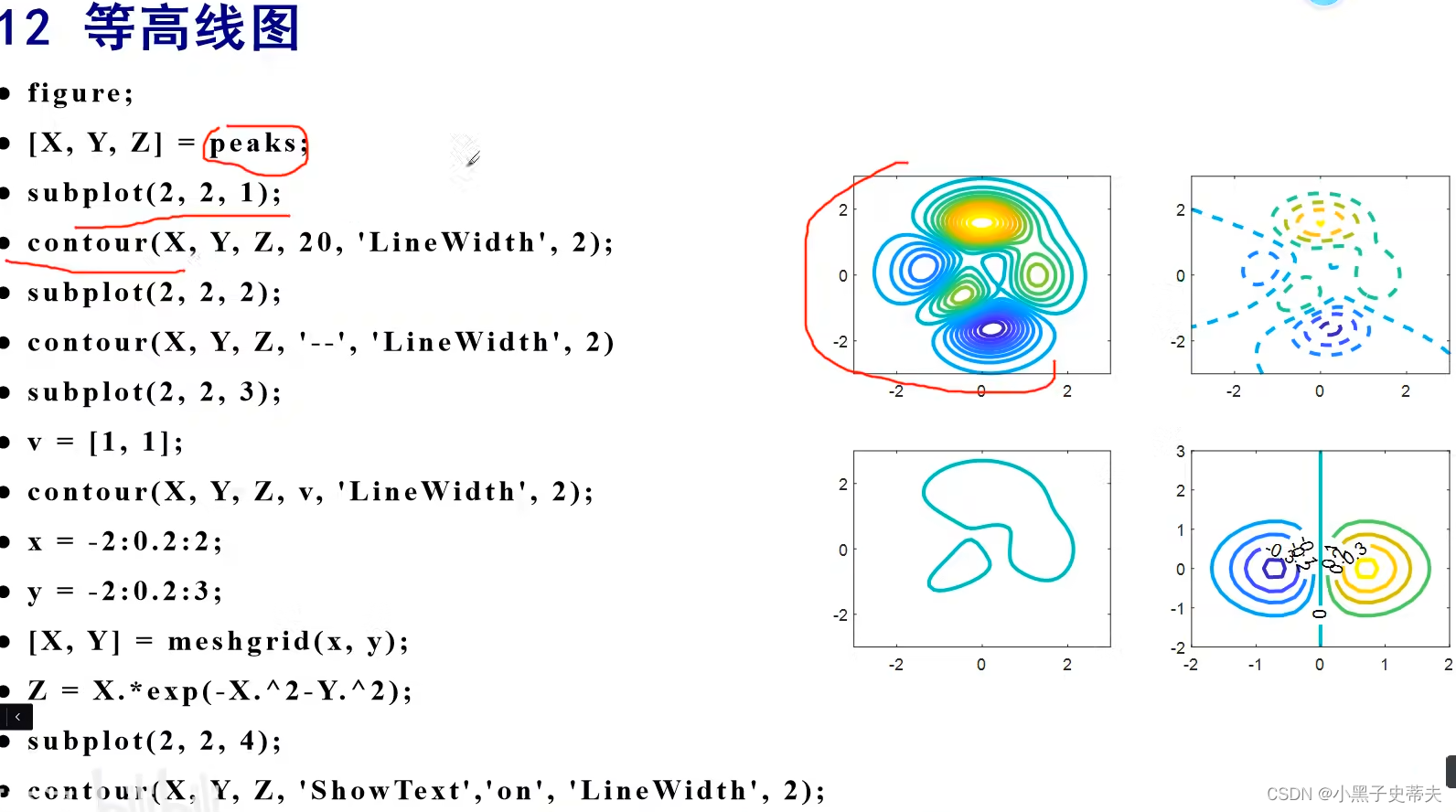
7.11.1 三维等高线图
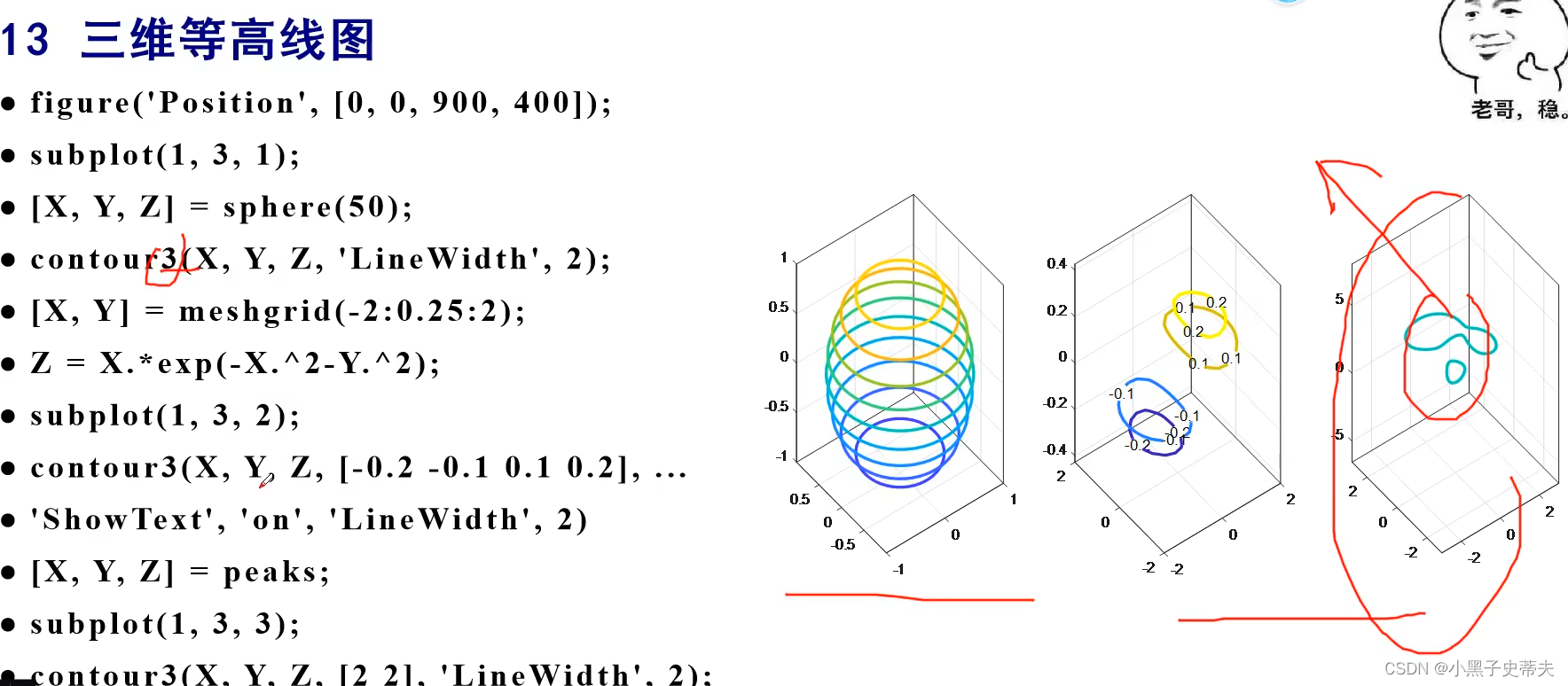
7.11.2 等高线填充图
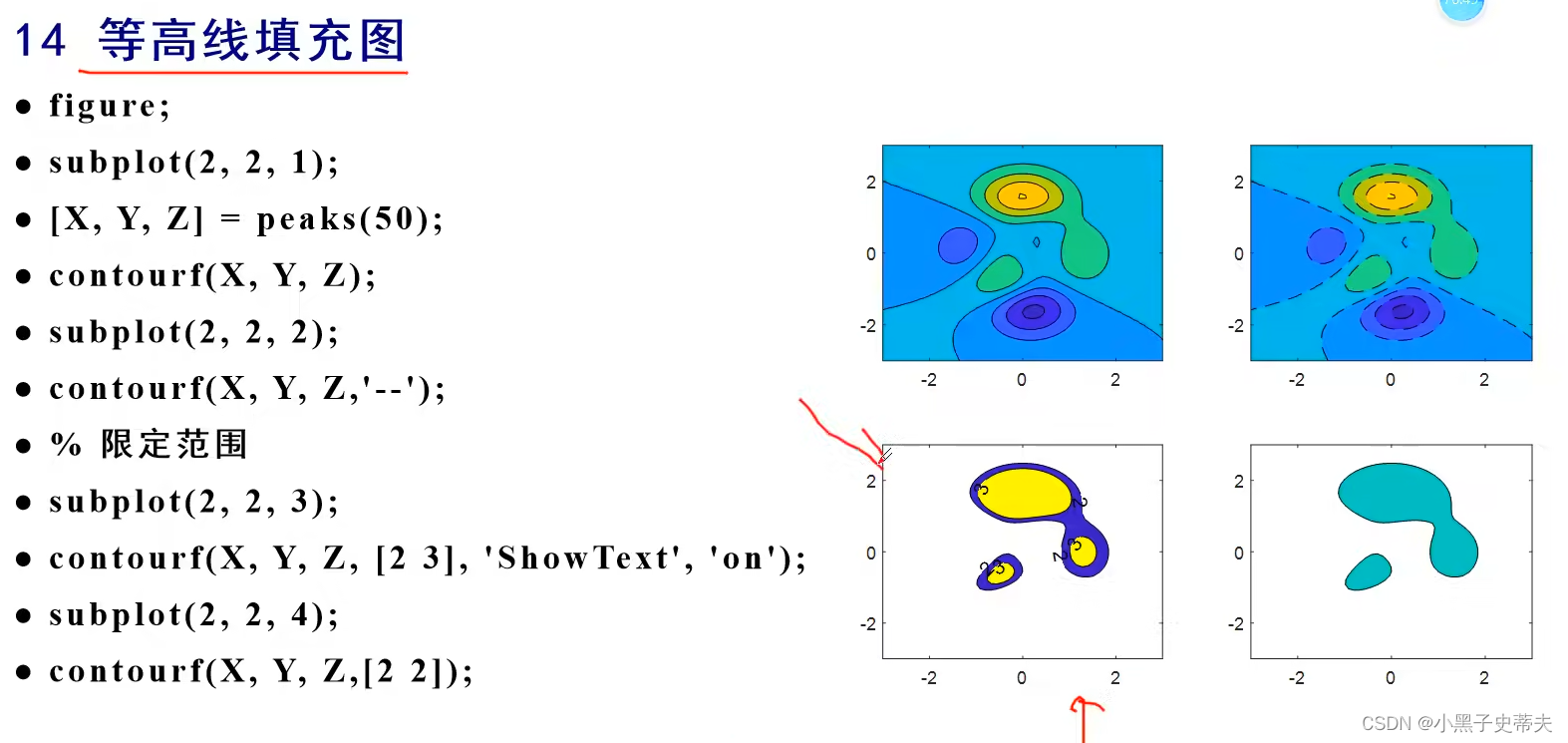
7.12 三维矢量场图
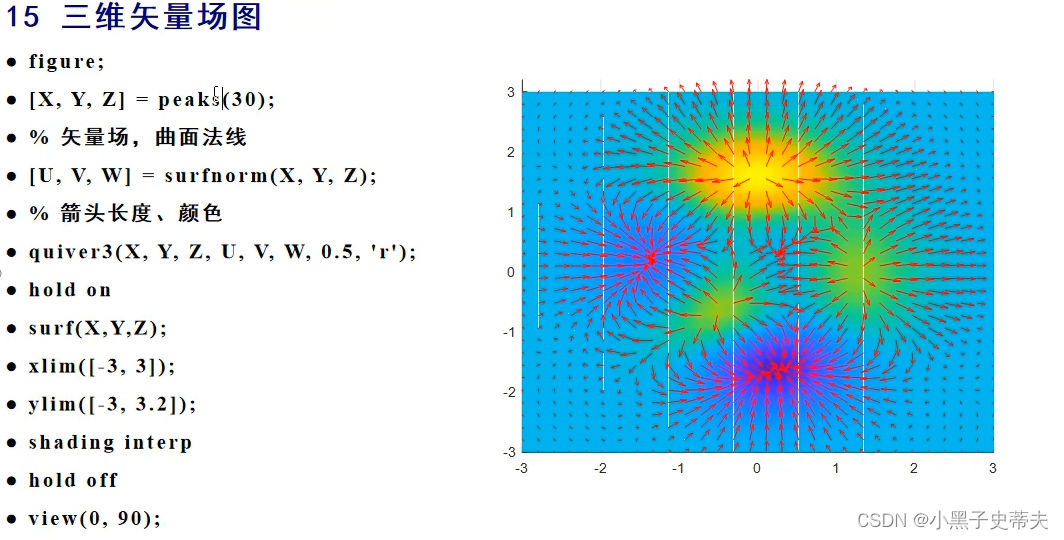
7.13 伪彩图+投影图
7.14 分子模型图

7.15 分形图
8. Matlab的数列与极限
8.1 sum 数组求和

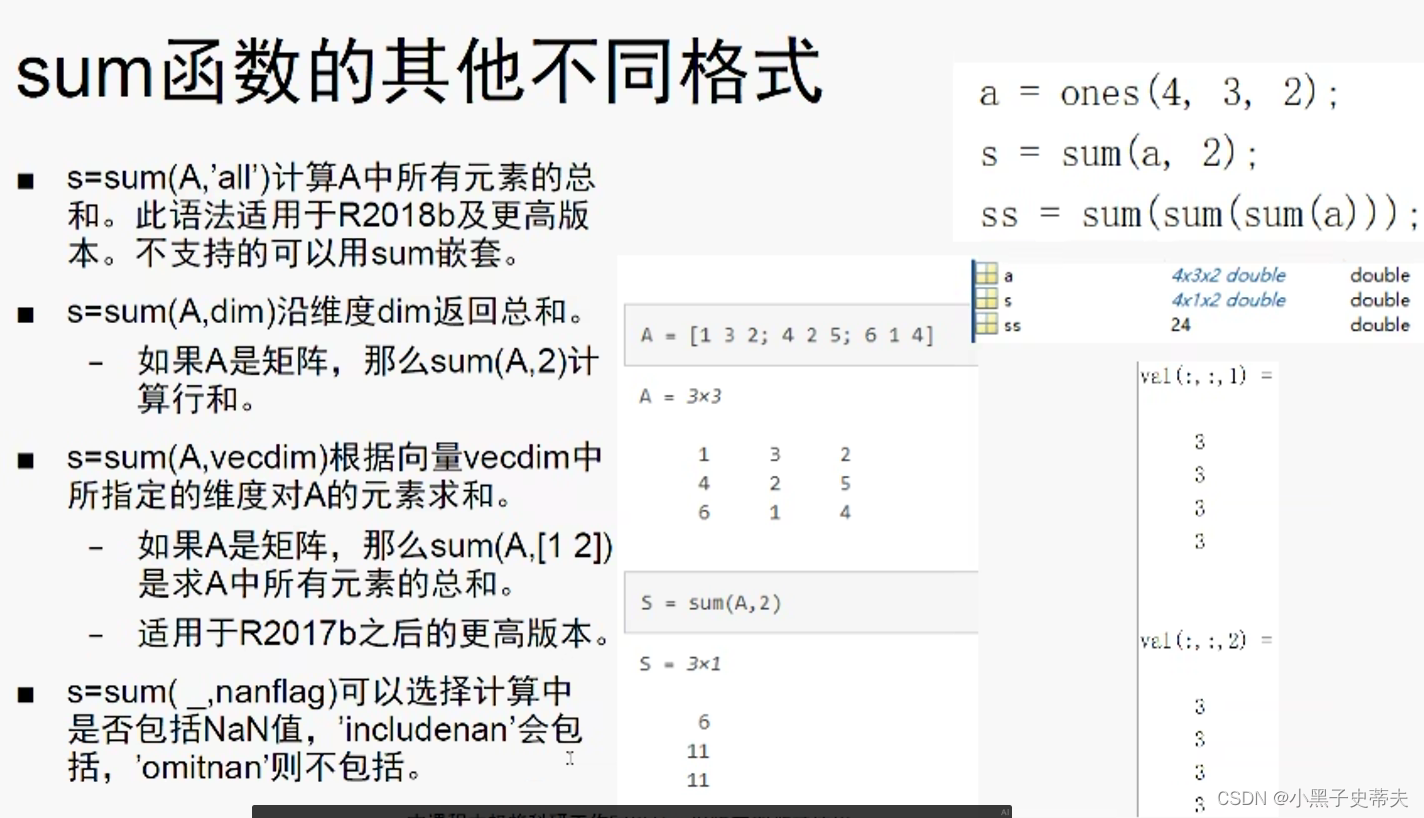
8.2 nansum 和 cumsum累积和
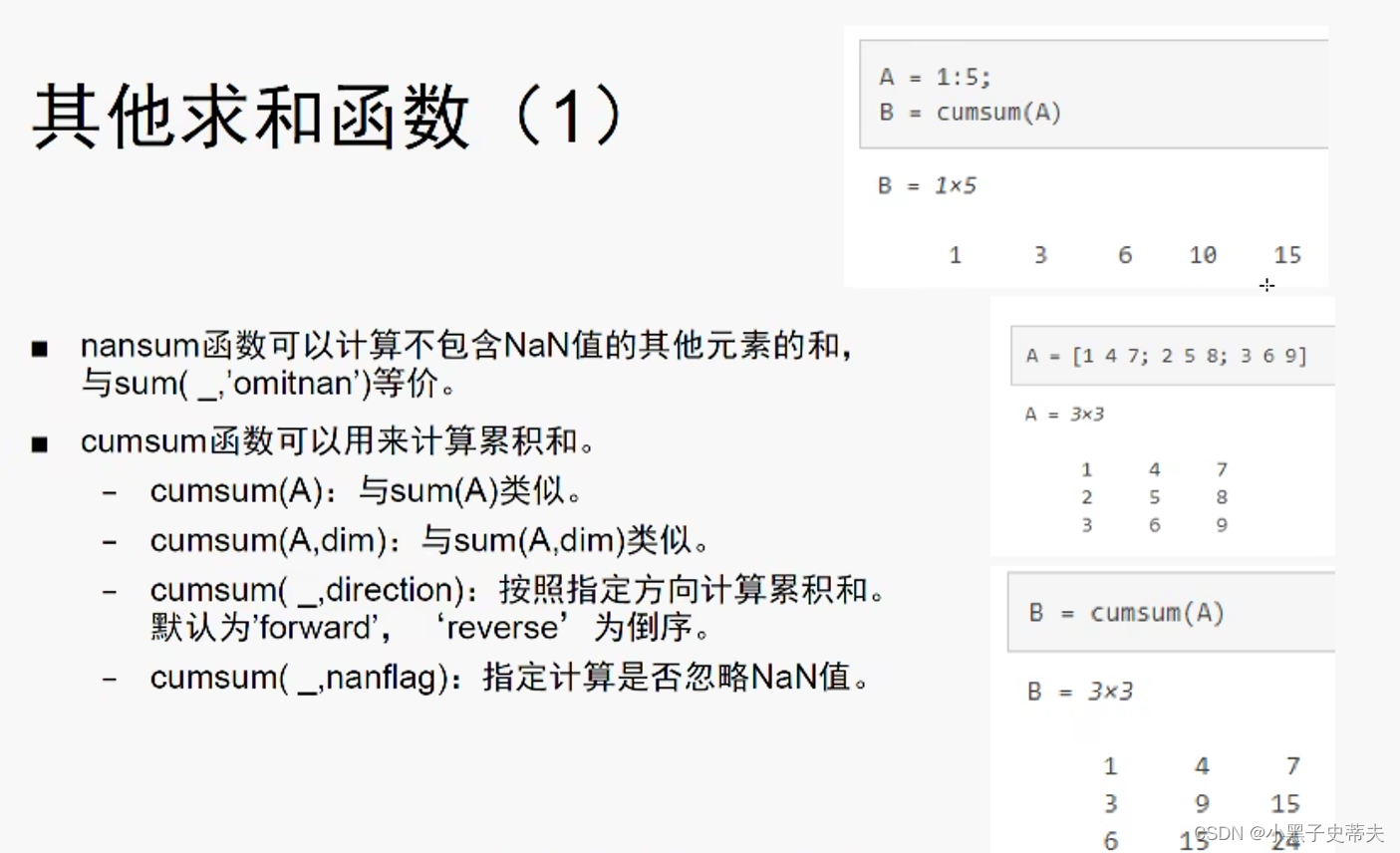
8.3 cumtrapz计算累积梯形积分

cumtrapz计算积分是会比实际值稍微大点
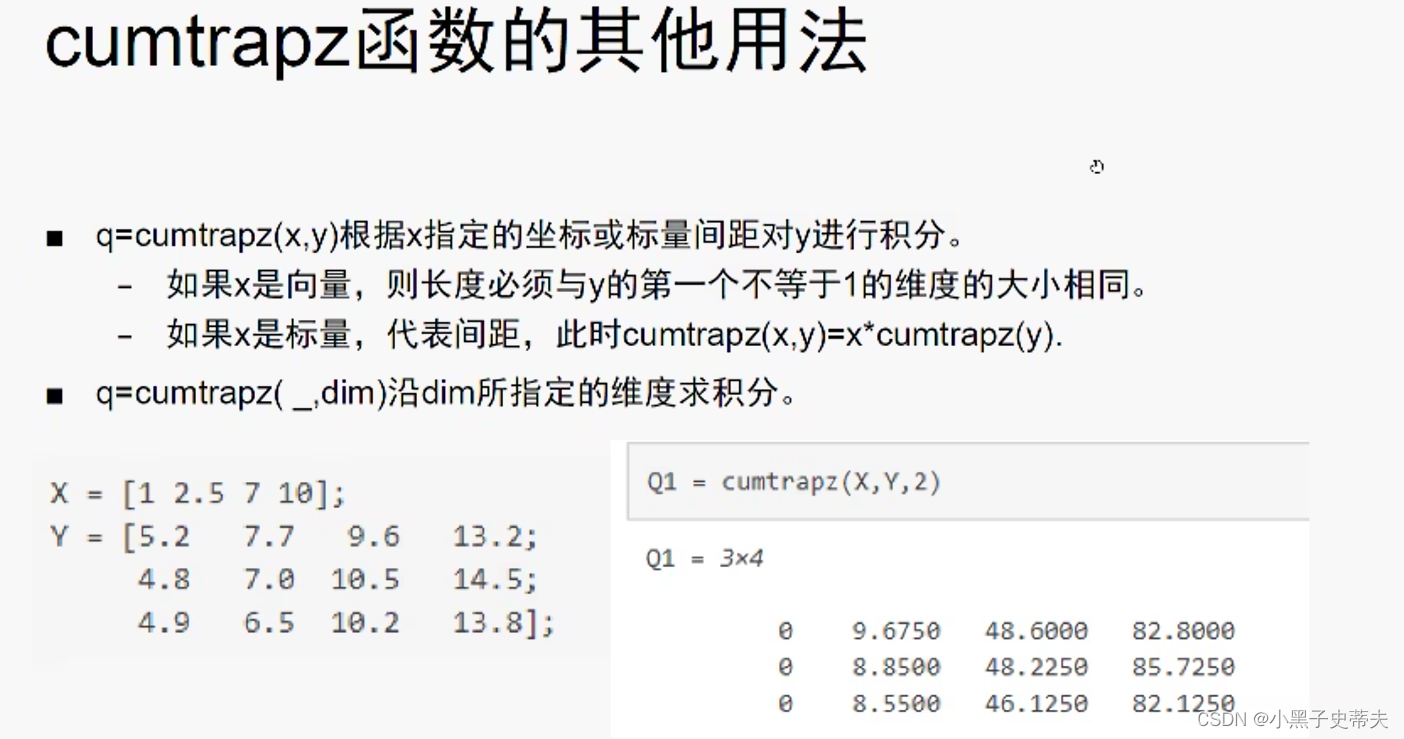
8.4 prod 求数组元素乘积
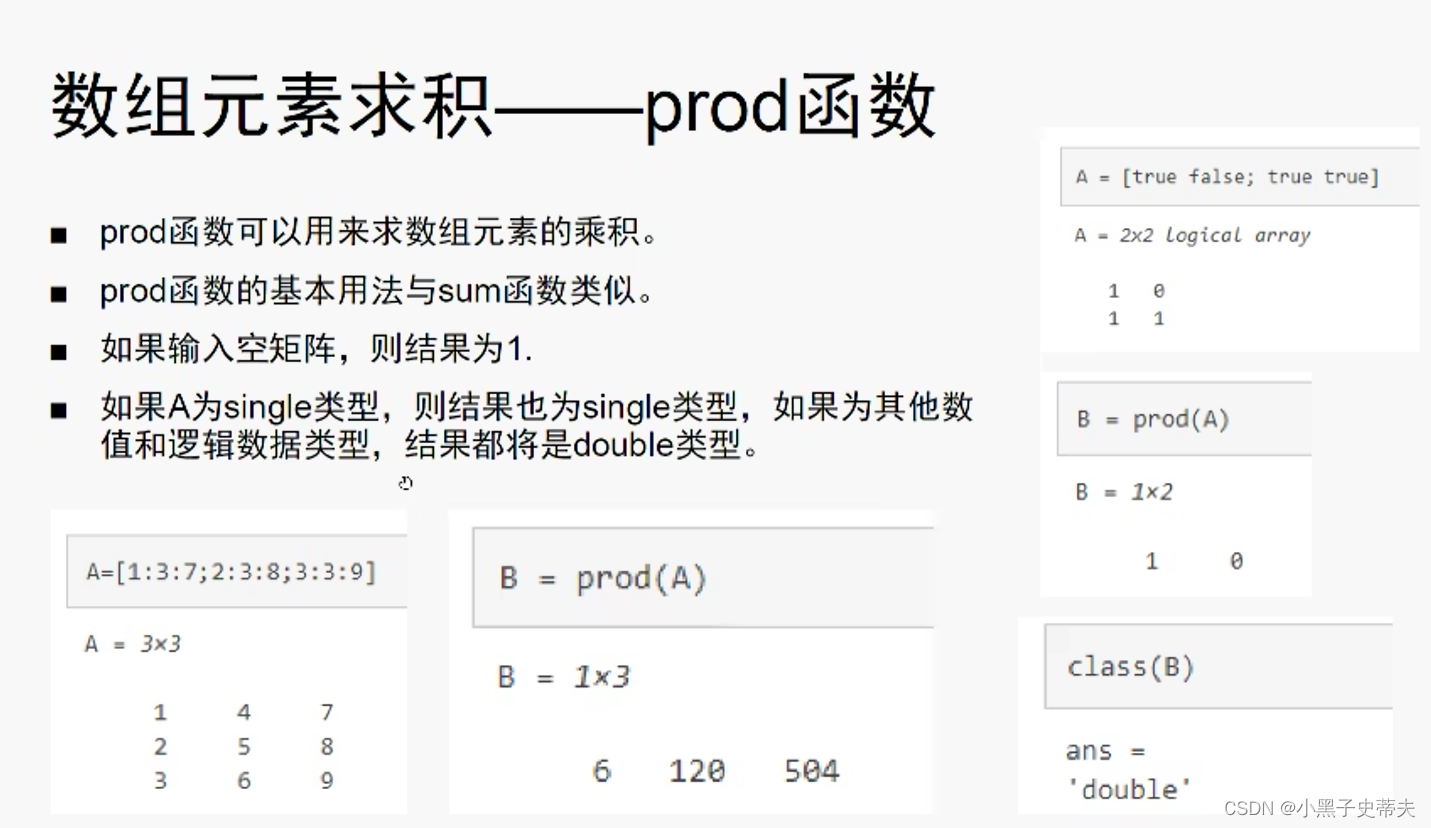
8.5 其他计算乘积相关的函数

8.6 limit极限 与 diff导数


- diff的差分用法

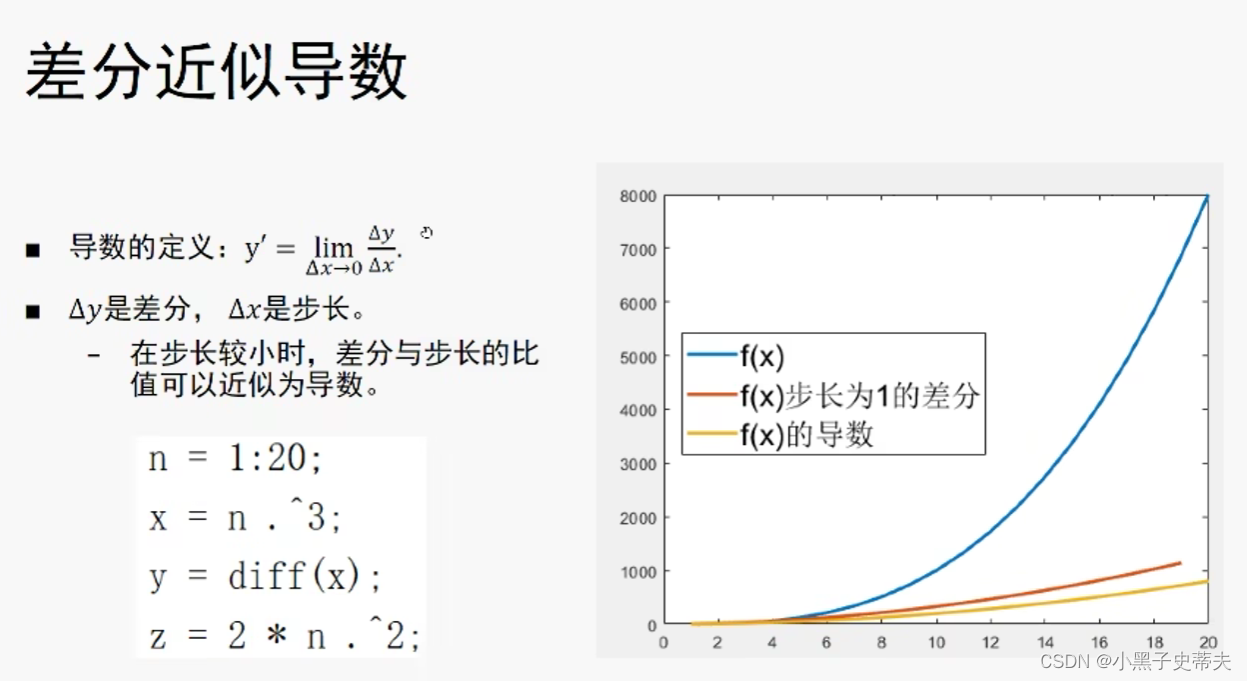
8.7 symsum 级数求和

- symsum用于计算不定积分

8.8 等差、等比数列求和

8.9 int 计算定积分
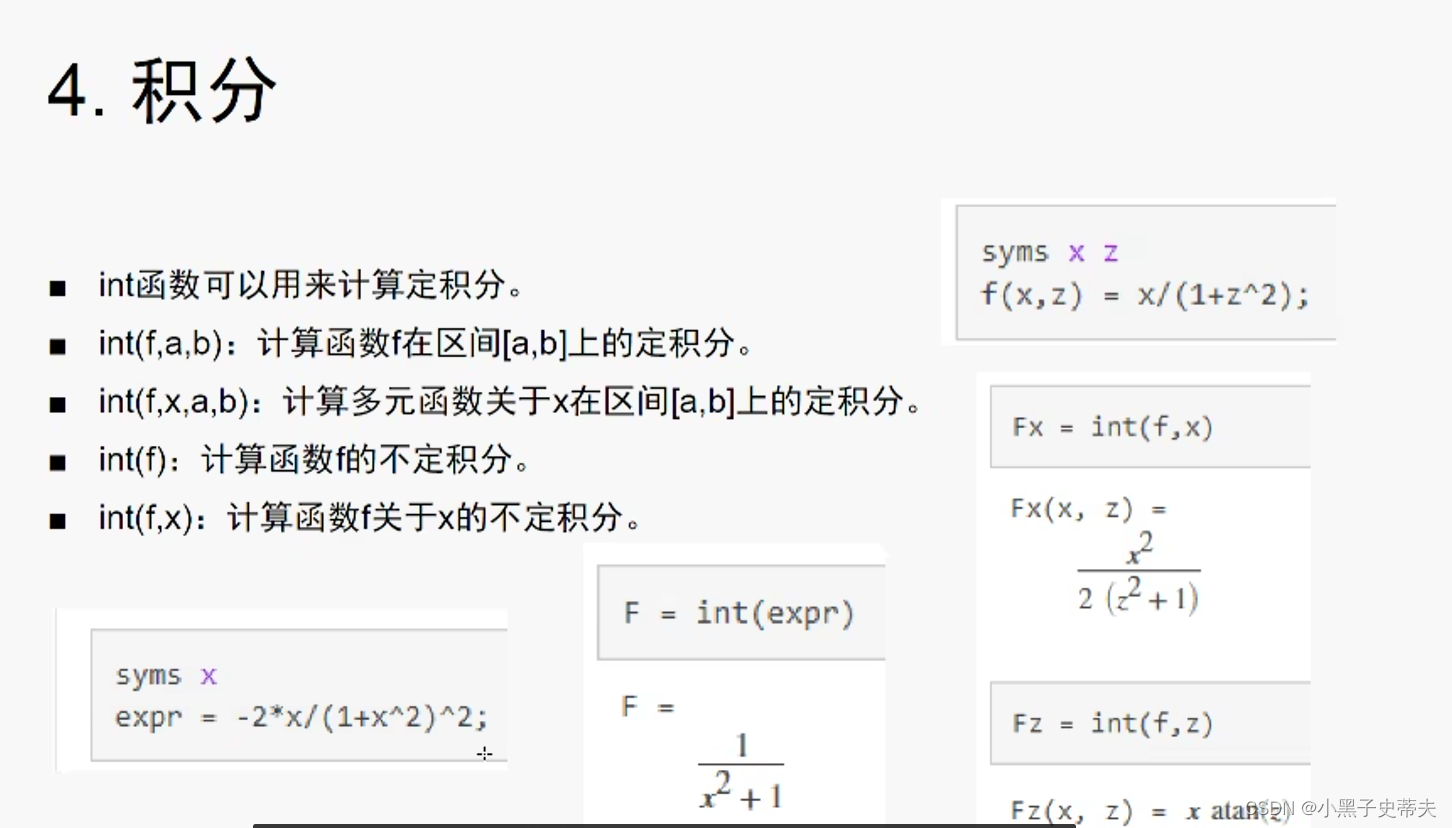
8.10 integral2 计算二重积分

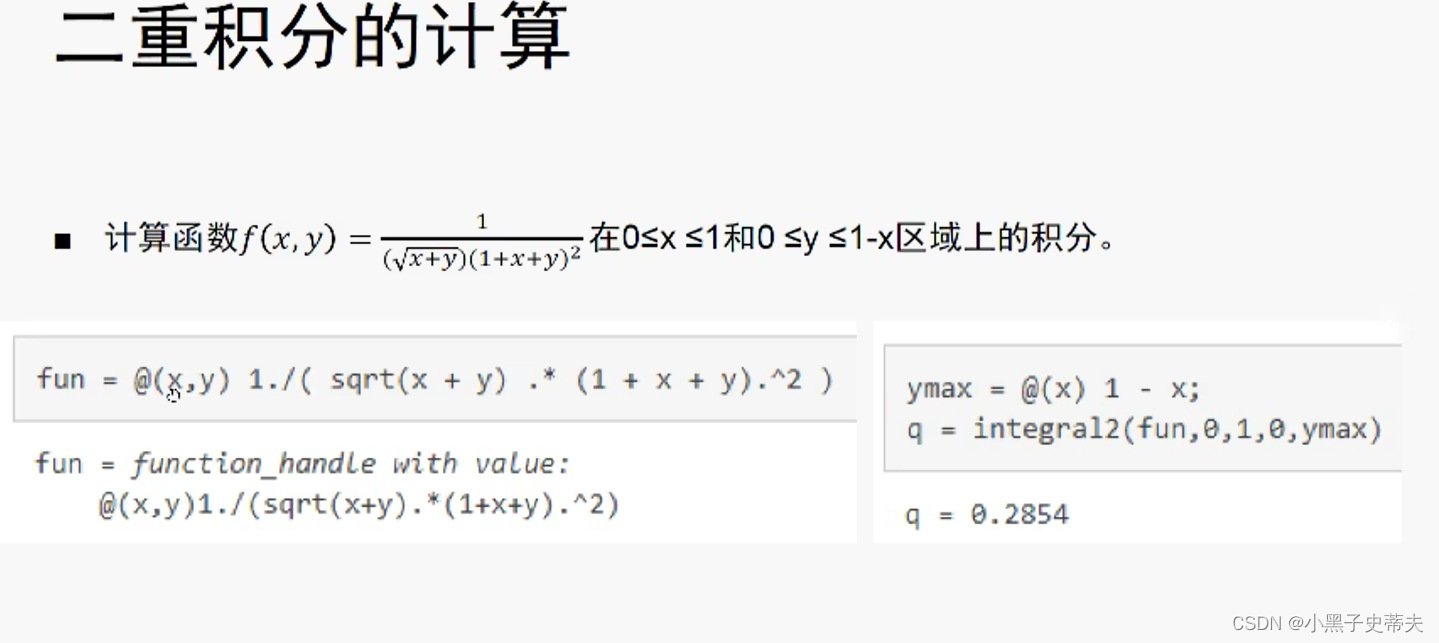
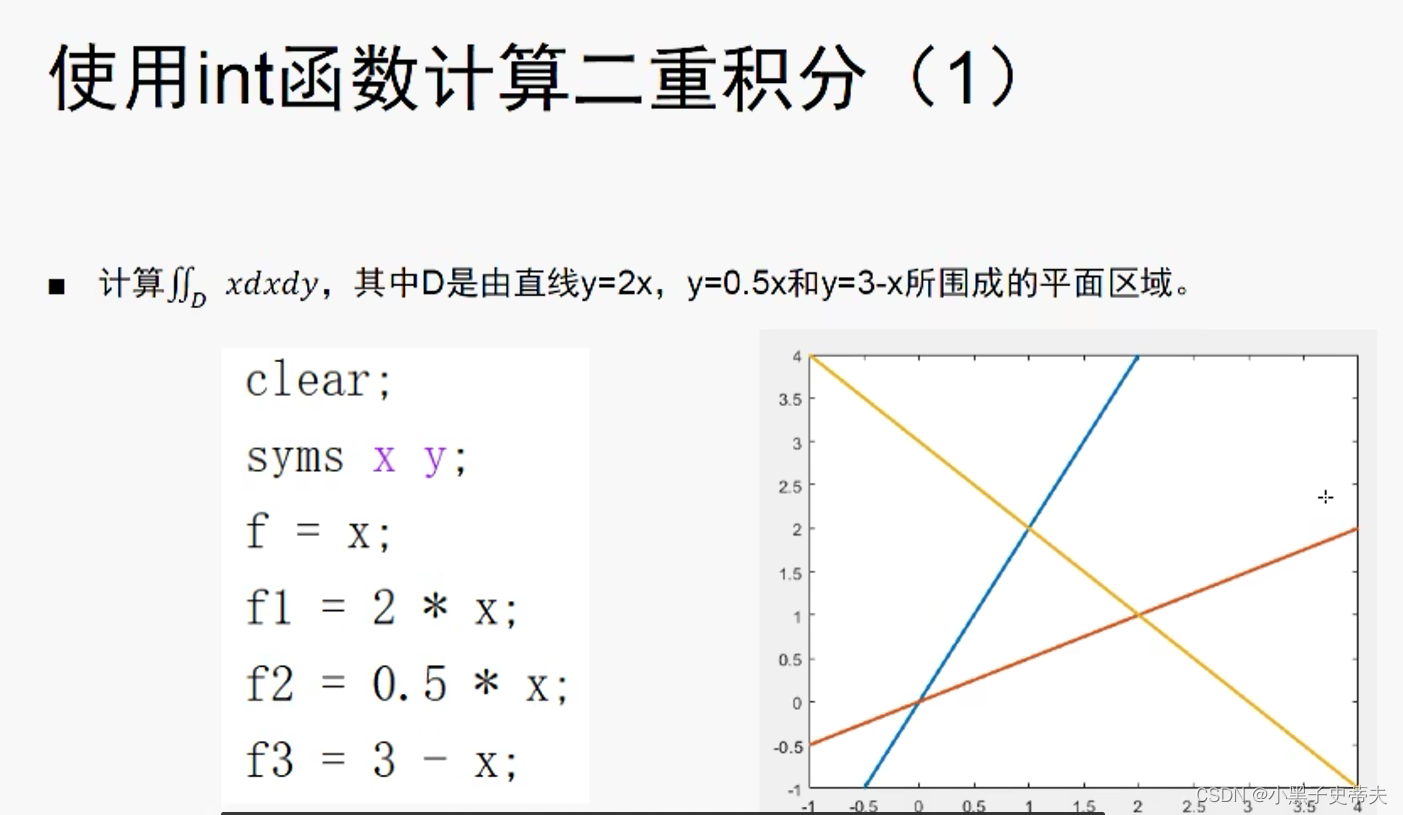
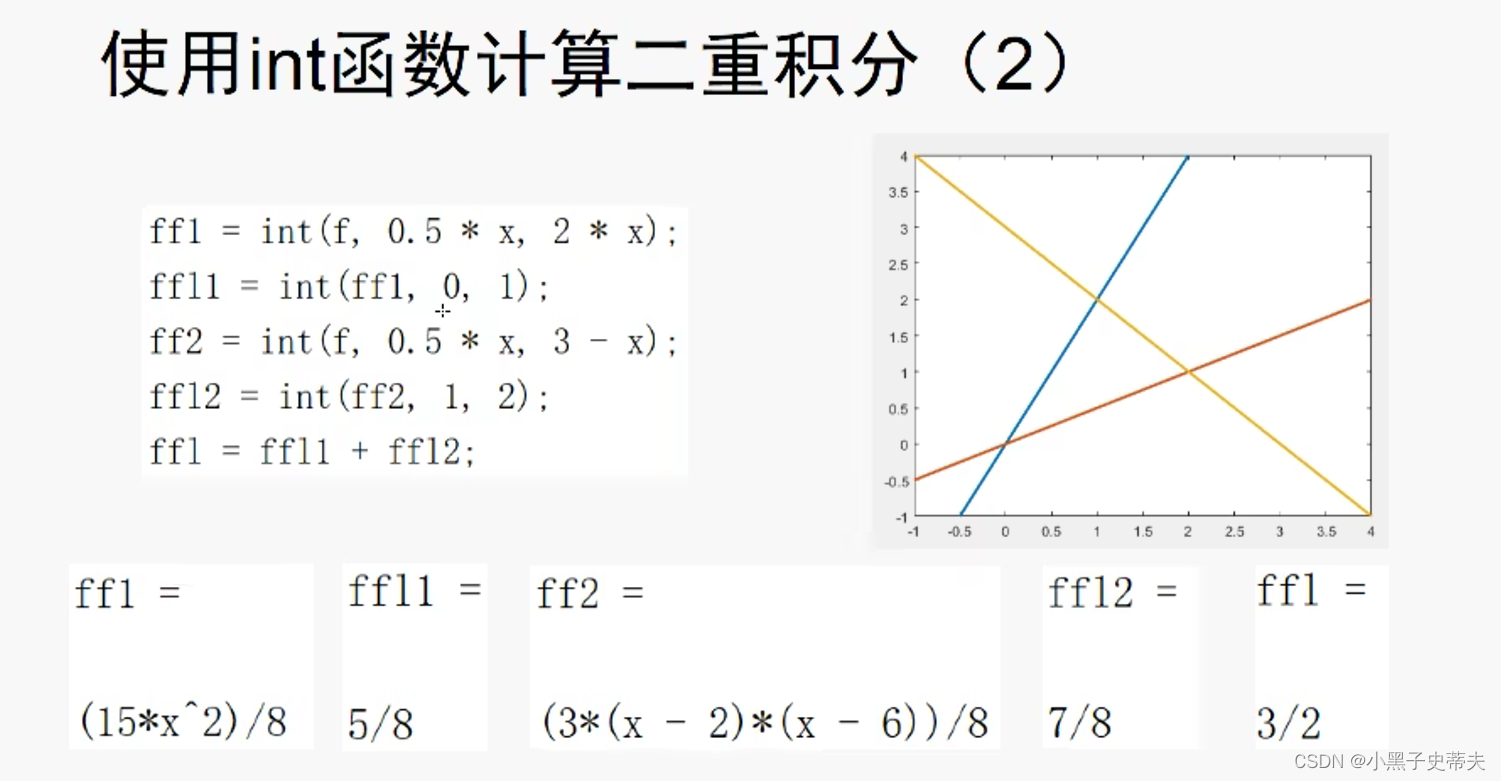
8.11 integral3 计算三重积分

8.12 taylor 泰勒展开

8.13 fourier 傅里叶变换

8.13.1 ffft 快速傅里叶变化

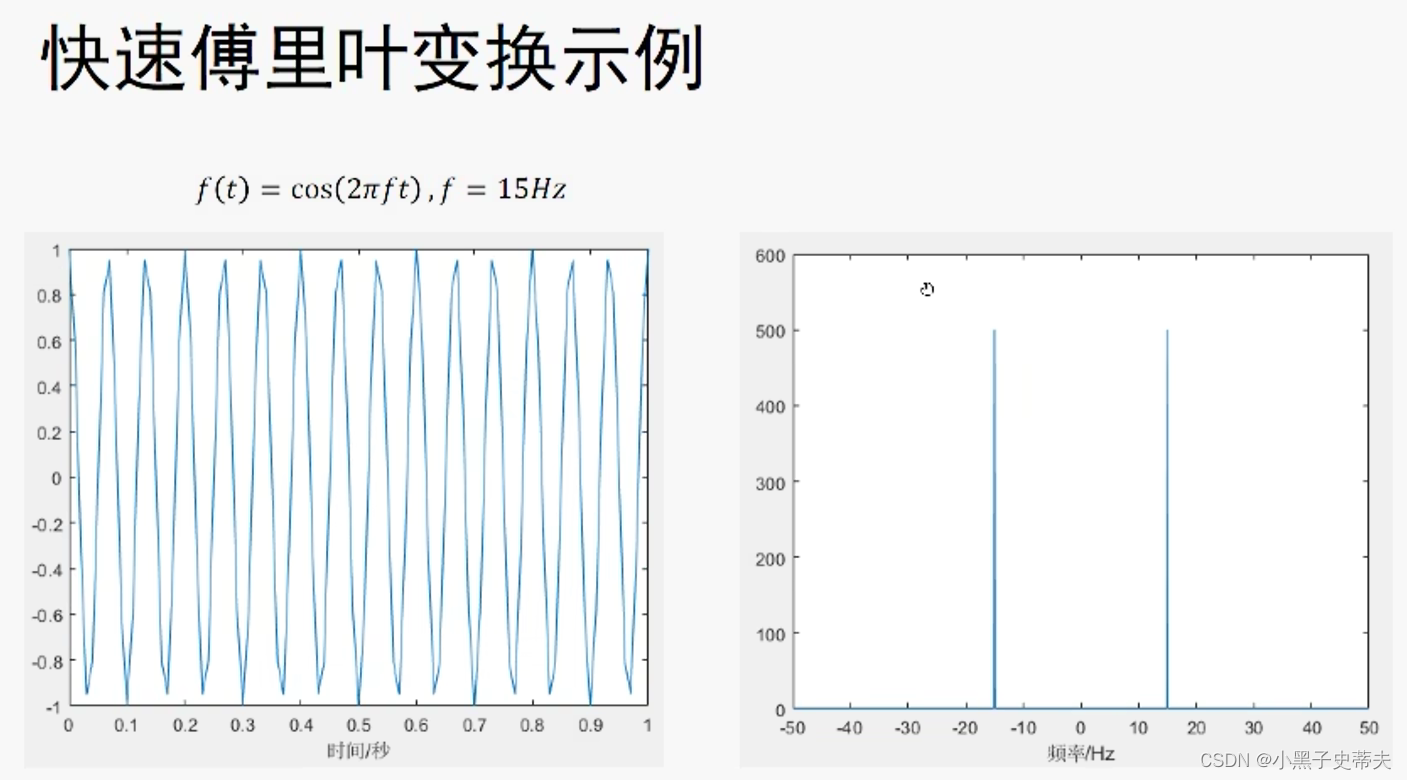
8.14 拉普拉斯变化

9. Matlab的微分方程


9.1 dsolve 求解微分方程




9.2 欧拉法


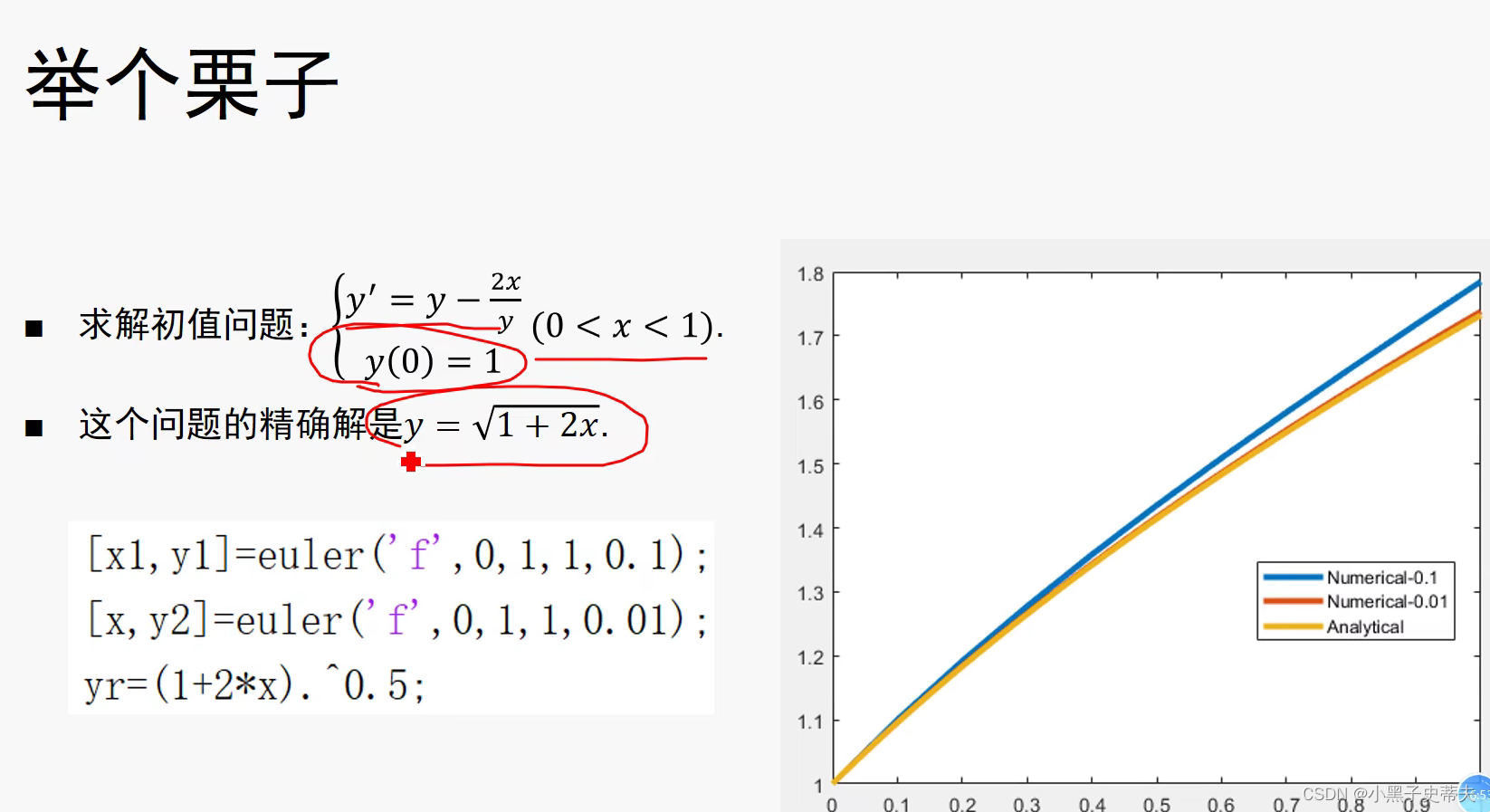
9.2.1 改进的欧拉法


9.3 ode龙格库塔法




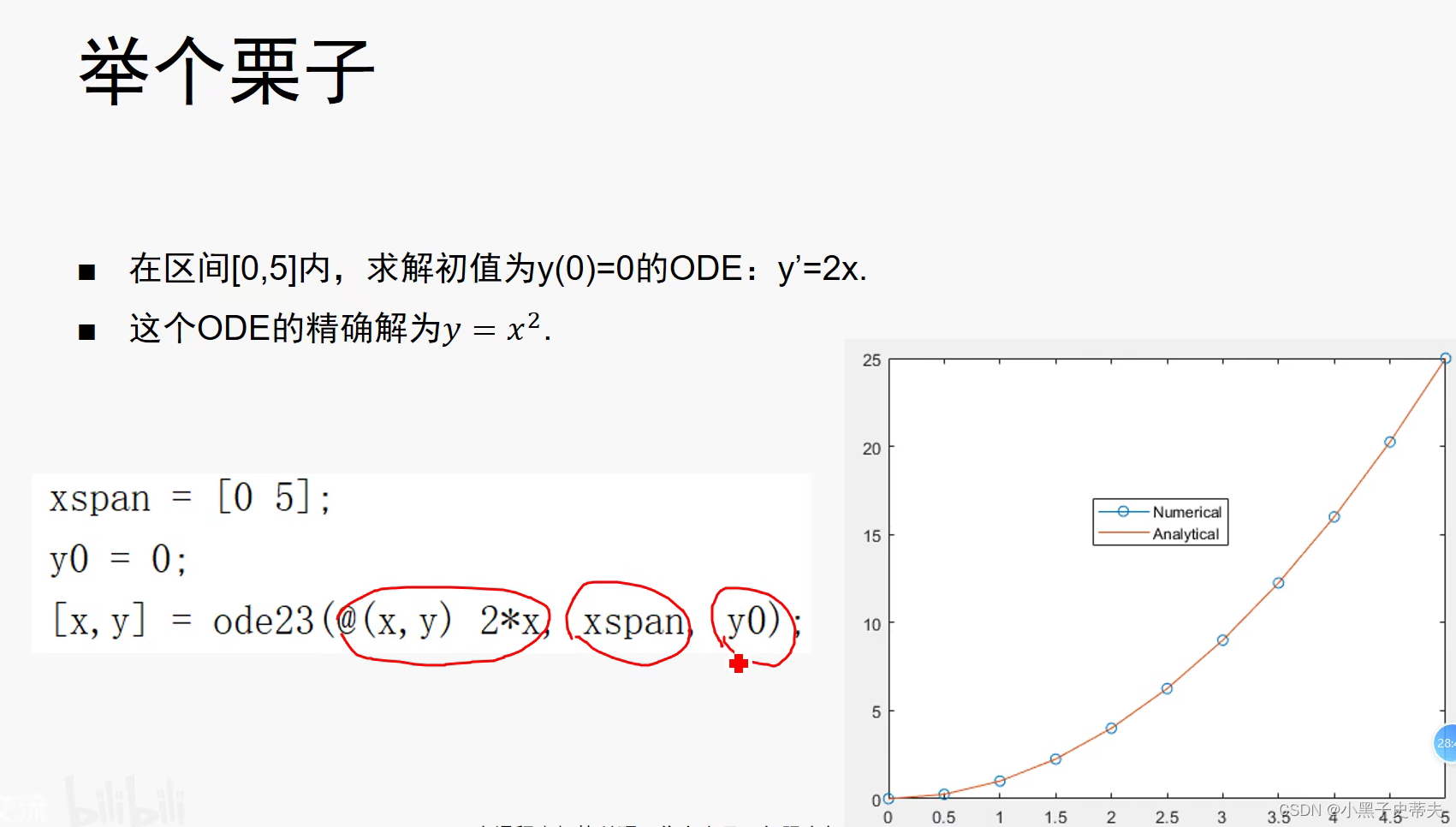
- 对比龙格和欧拉的区别:
龙格比欧拉法更加精确一些
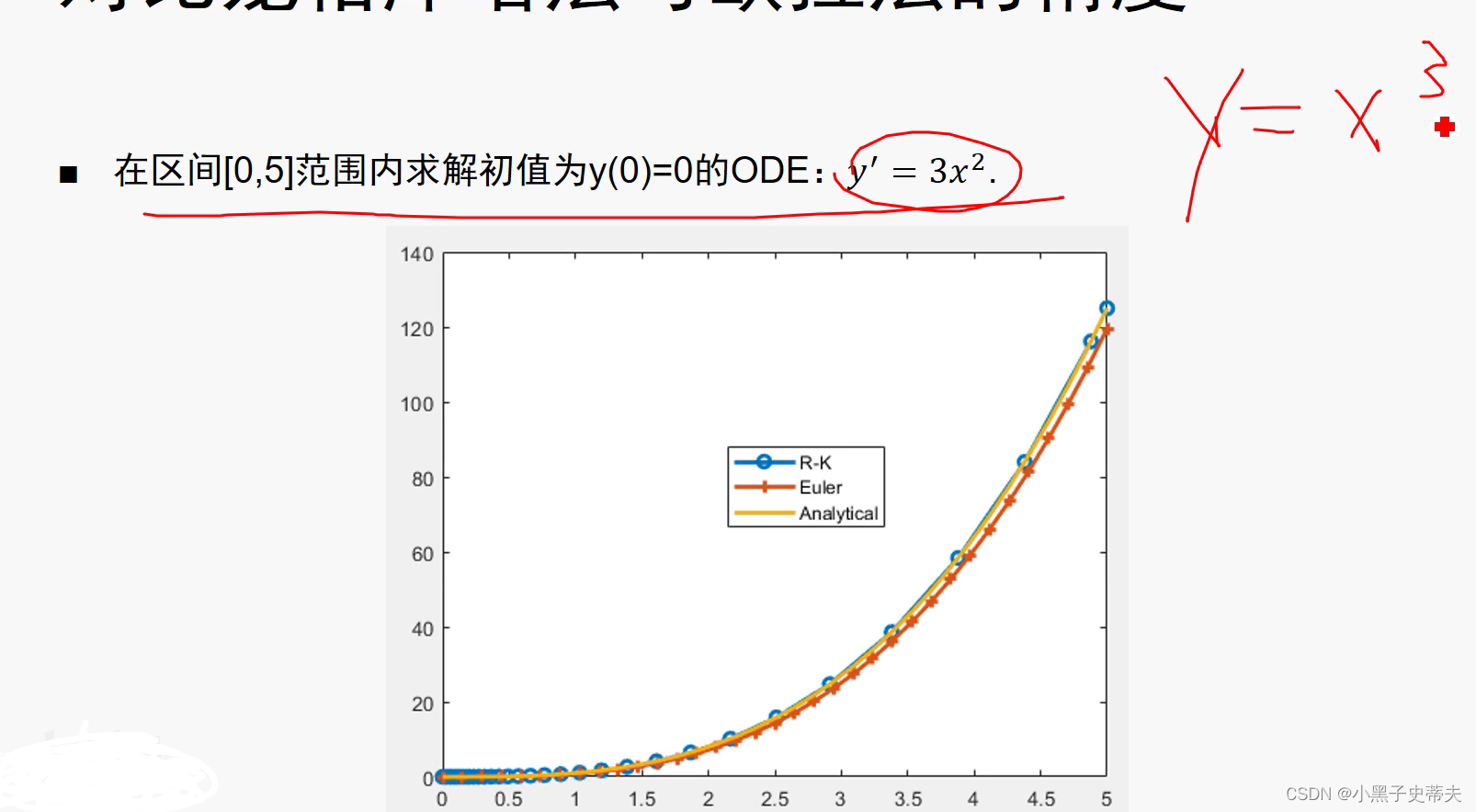

9.4 偏微分方程


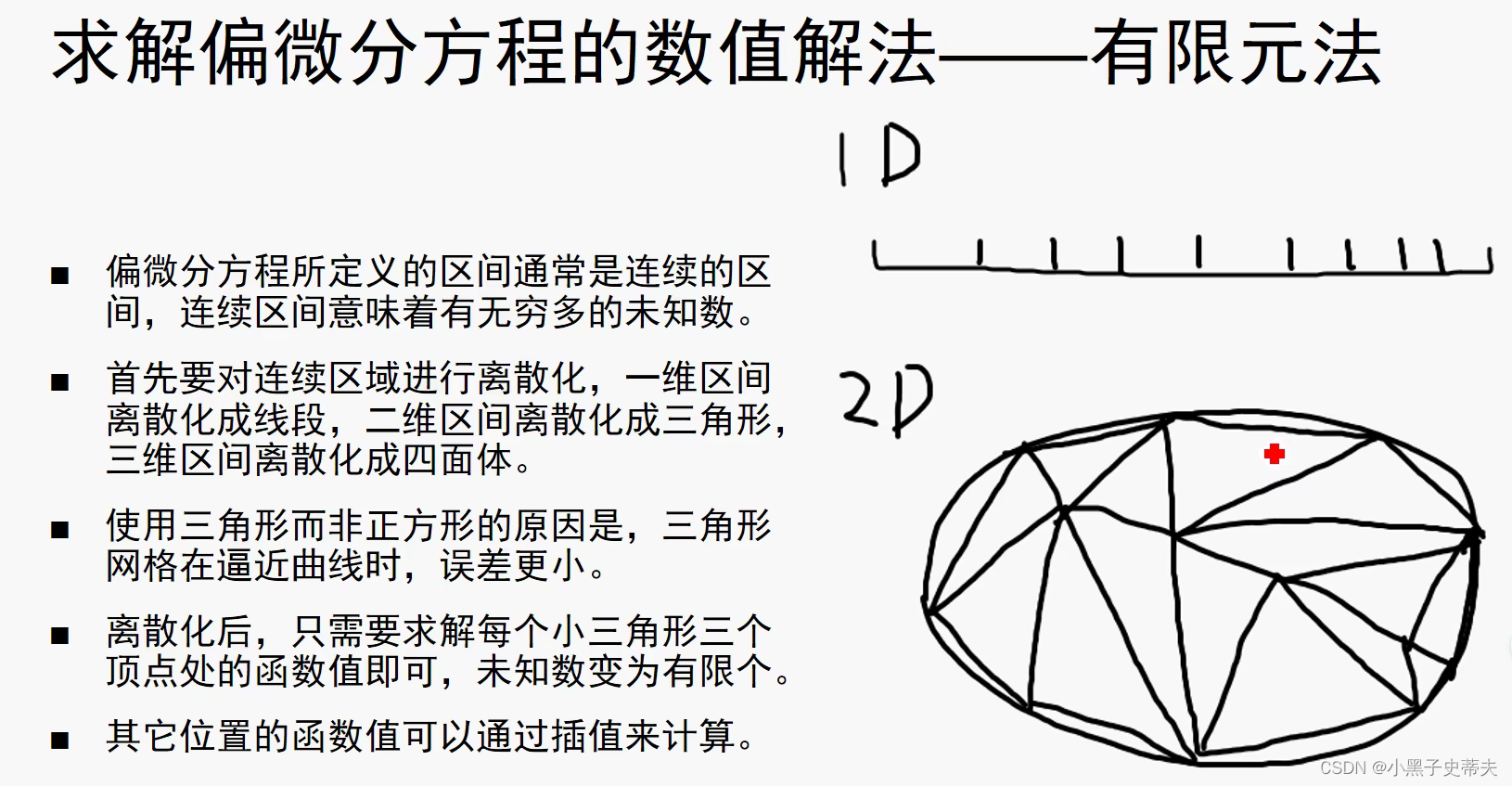
9.4.1 有限元法

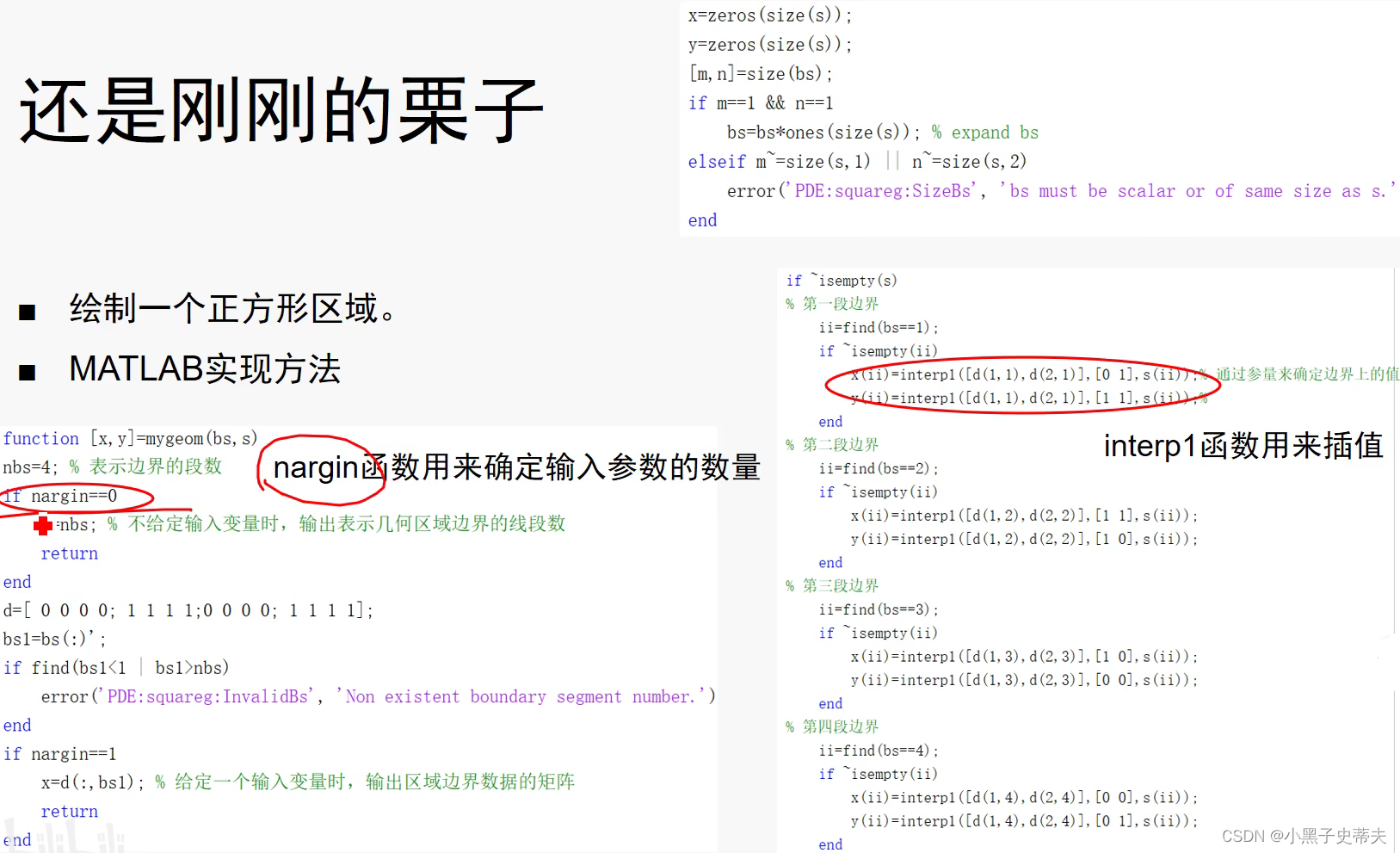
9.4.2 求解区域的设置

9.4.3 求解区域的网格化

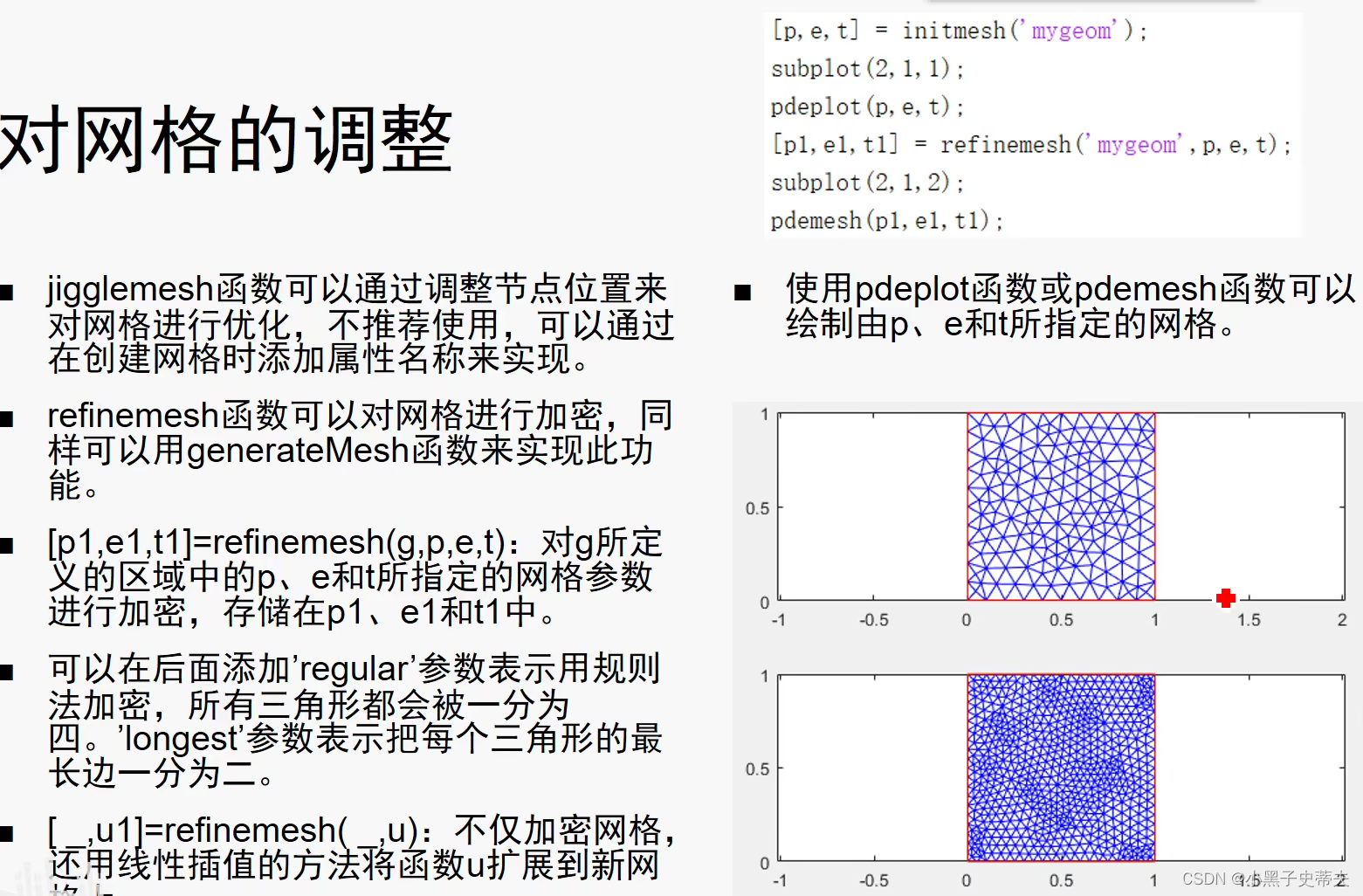
- 设置边界条件


9.4.4 求解椭圆型PDE

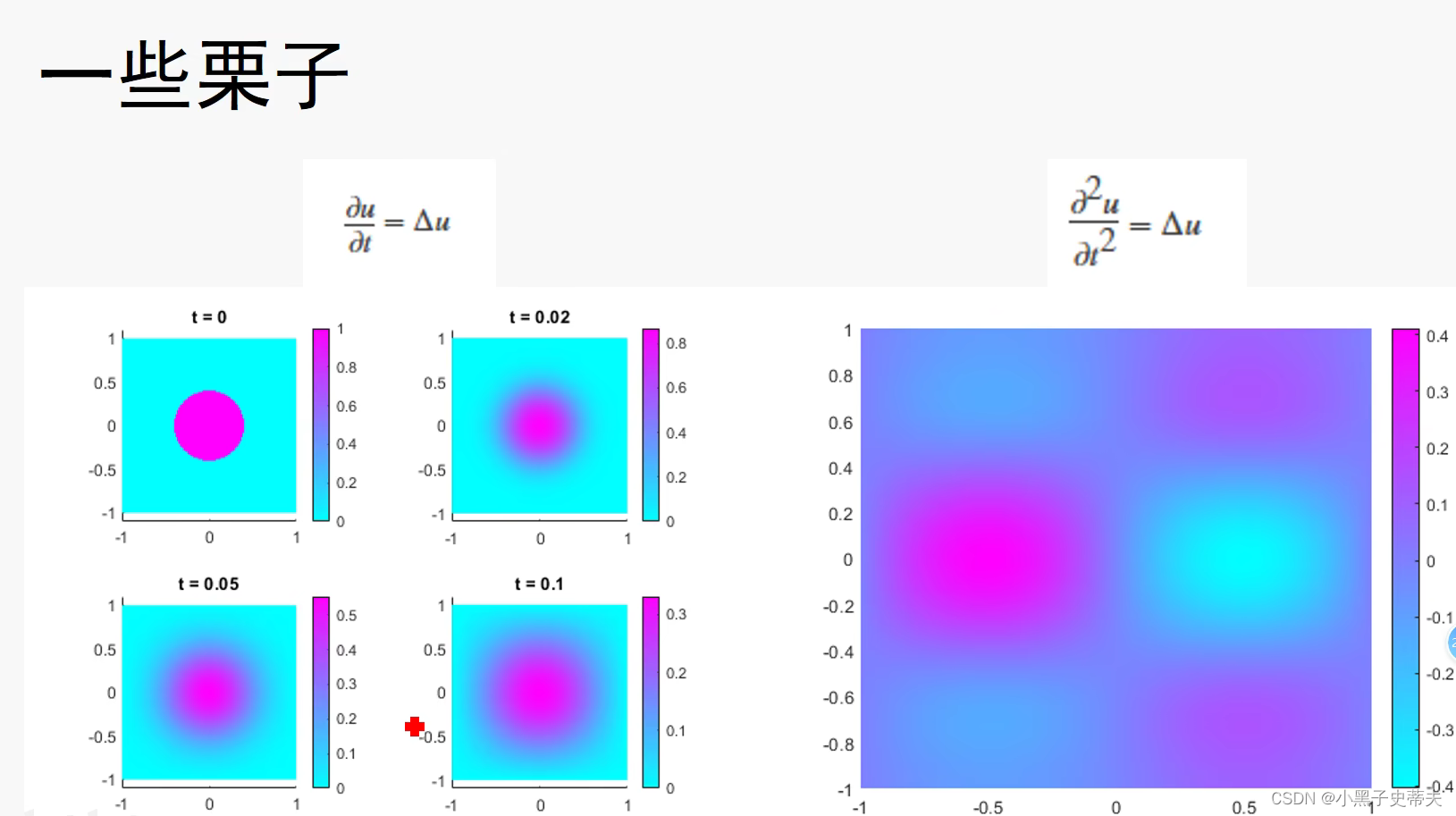
9.4.5 pdetool辅助实现
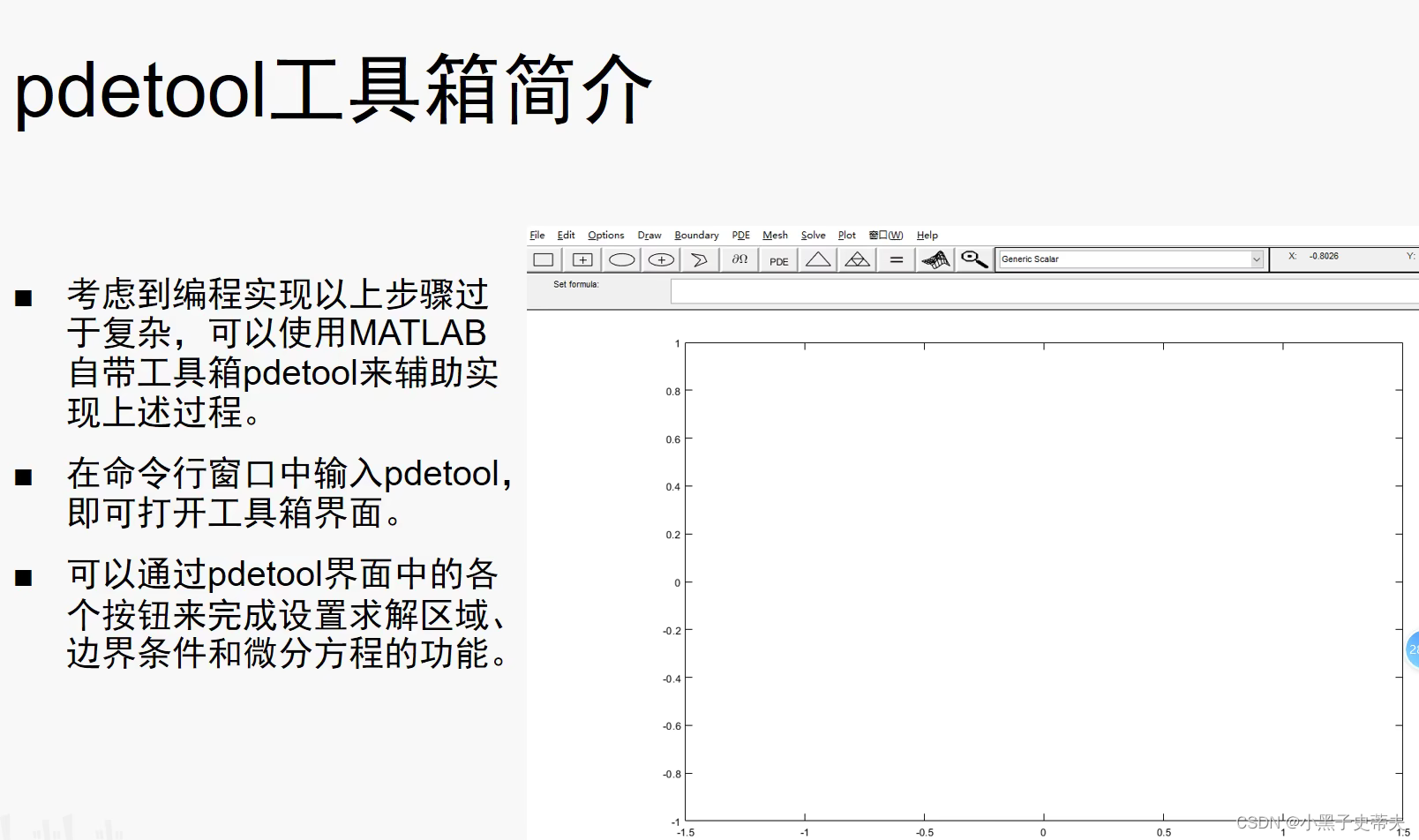
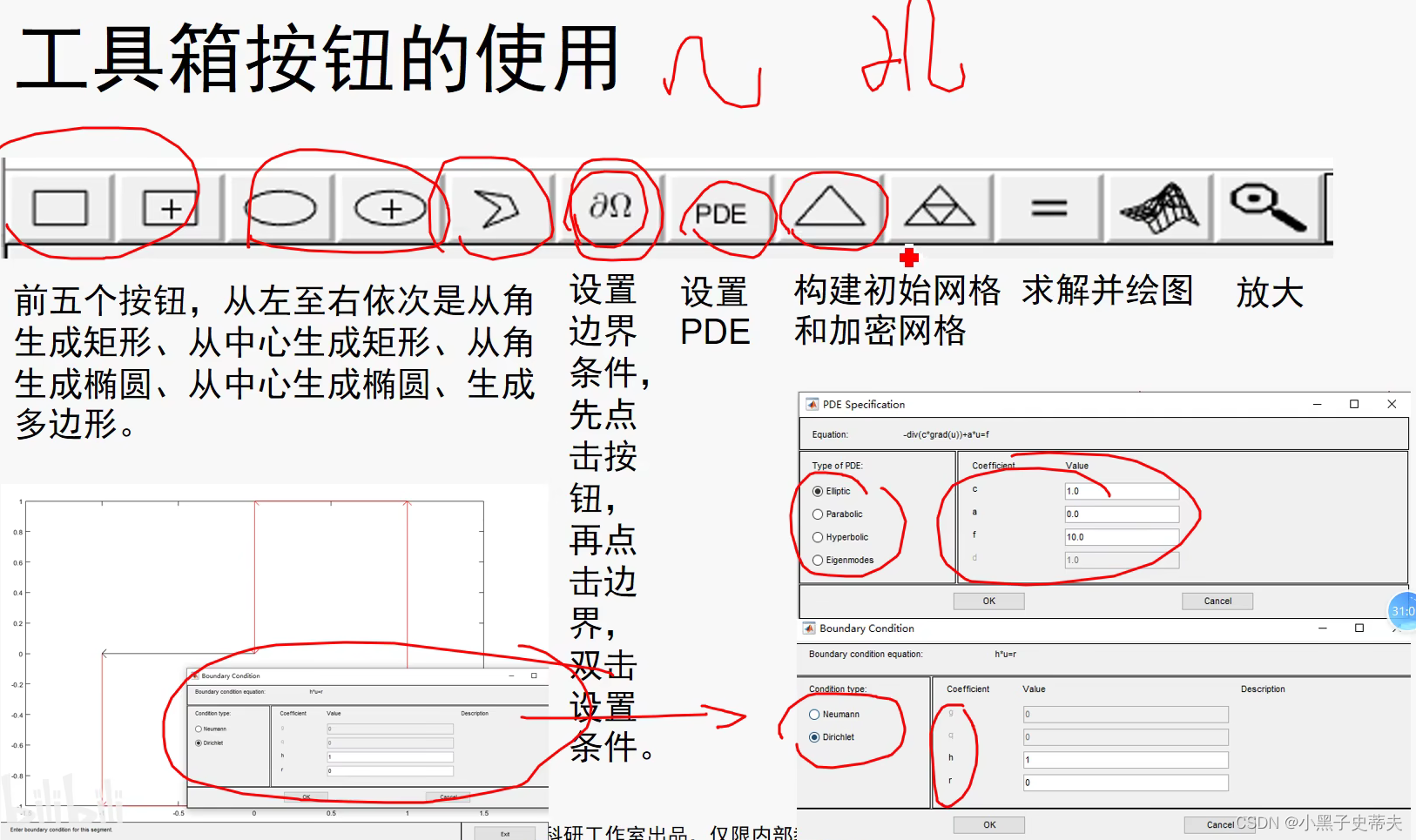
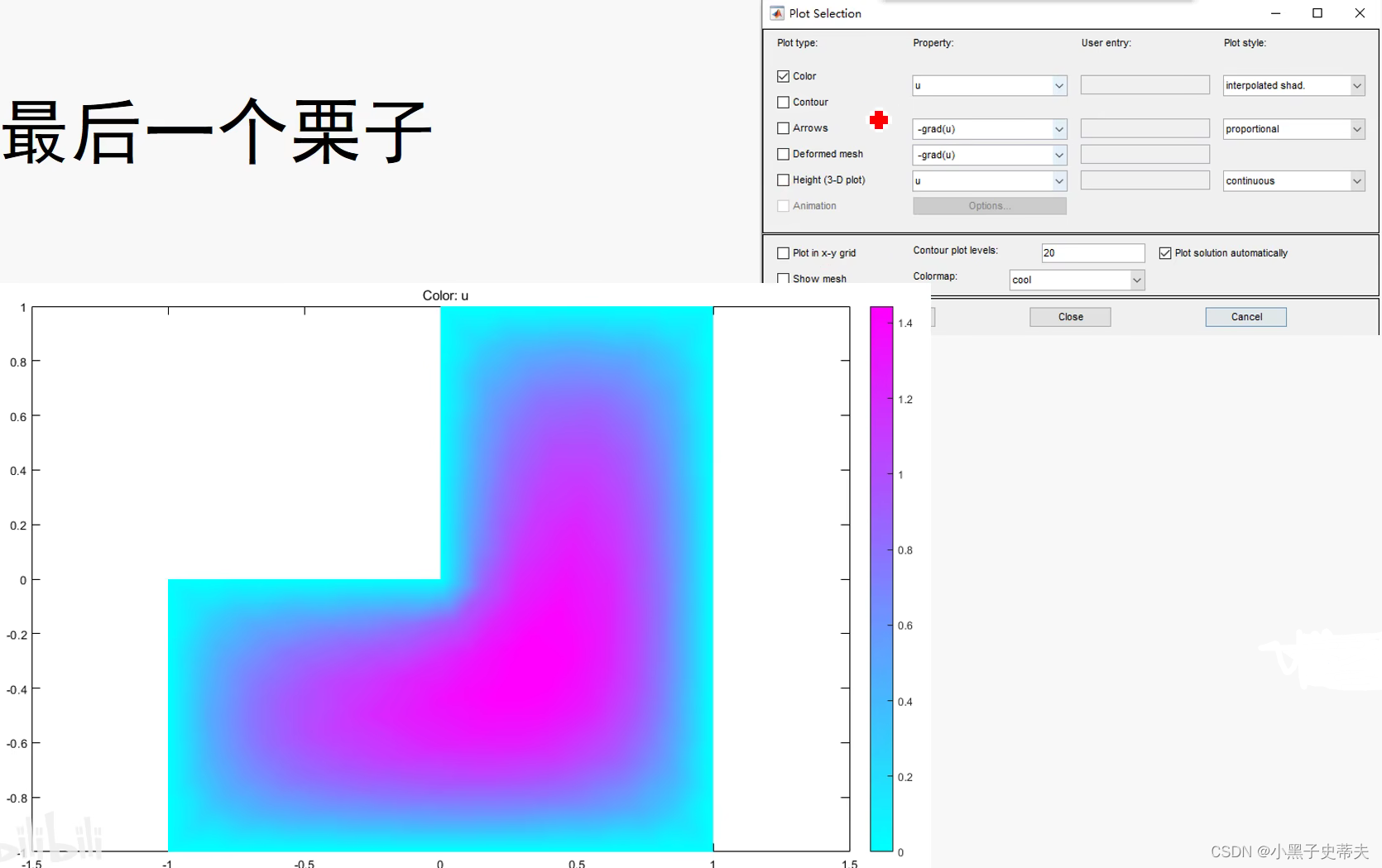

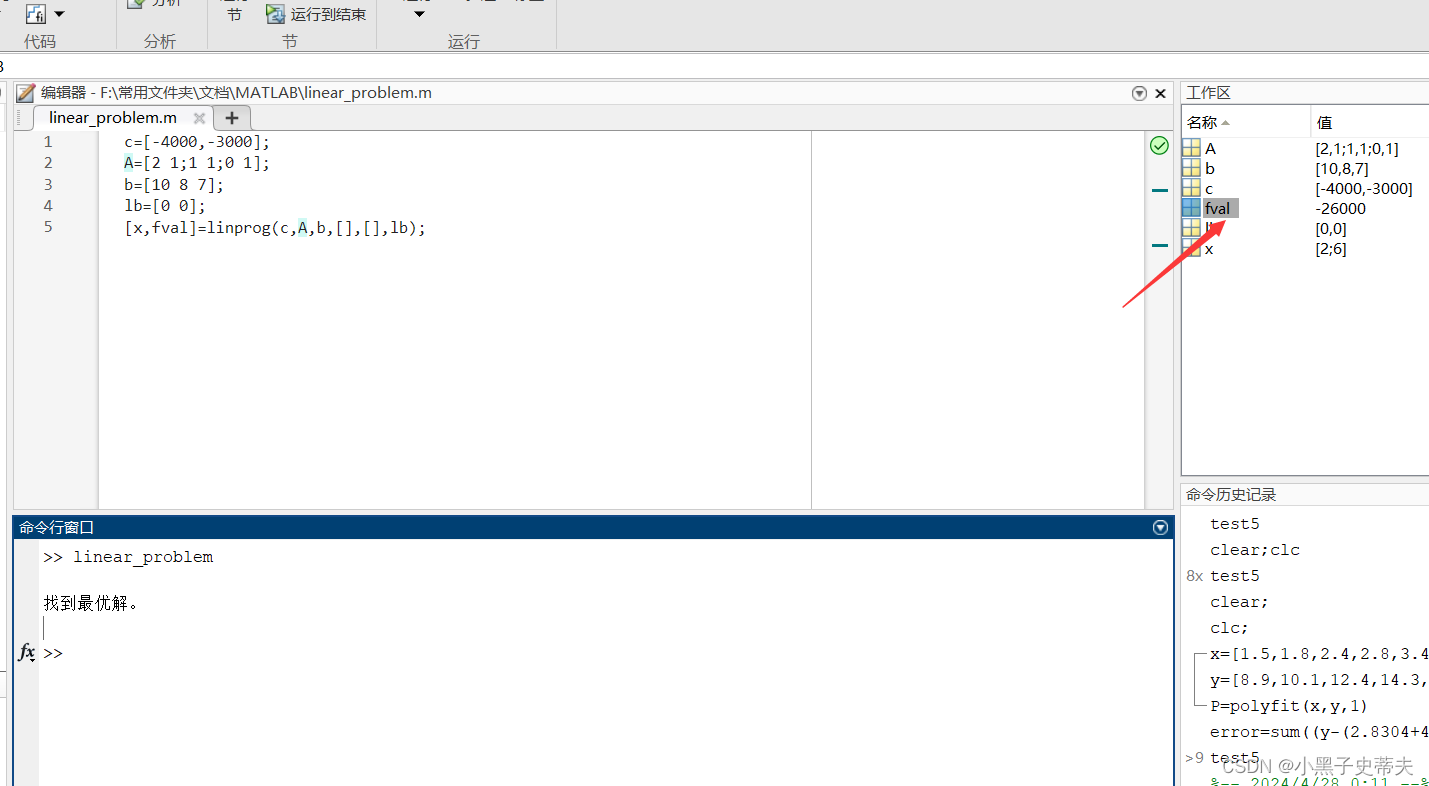
10. matlab的线性规划

- 例子:




在上述例1.2.1和例1.2.2的数学模型中,目标函数和约束函数都是线性的,称之为线性规划问题;而例1.2.3和例1.2.4 的数学模型中含有非线性函数,因此称为非线性规划问题。
在线性规划与非线性规划中,满足约束条件的点称为可行点,全体可行点组成的集合称为可行集或可行域.如果一个问题的可行集是整个空间.那么此问题就称为无约束问题.

10.1 范数



10.2 序列


10.3 梯度

10.4 凸集和凸函数


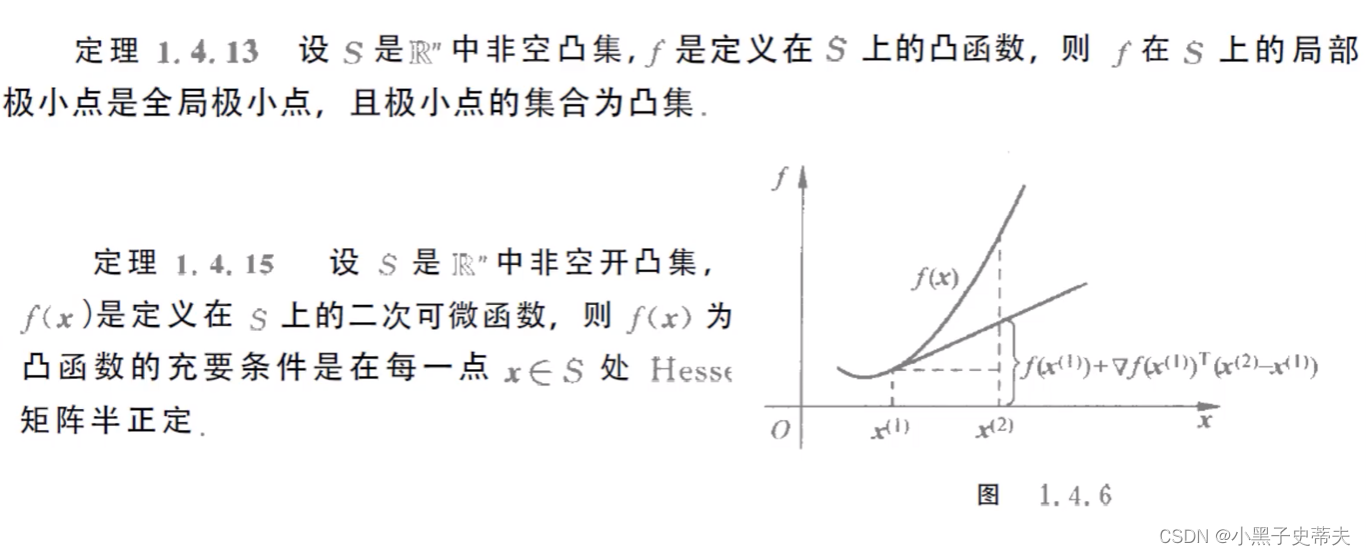

10.5 凸规划

10.6 线性规划的标准








题目步骤:



- 例子:

10.7 例题