一,堆排序
堆排序是一种基于比较的排序算法,它利用堆这种数据结构所设计。
堆是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父结点。
堆排序可以分为两个主要步骤:建堆和用堆删除思想调整排序。
1.堆排序实现思路
- 建堆
- 初始时,将待排序序列构造成一个大顶堆(或小顶堆)。此时,整个序列的最大值(或最小值)就是堆顶的根结点。
- 通常从最后一个非叶子结点开始调整,将其调整为一个堆,然后向前依次调整每一个非叶子结点,直到整个序列都成为一个堆。
- 堆调整排序
- 此时整个序列的最大值(或最小值)就是堆顶的根结点。将其与末尾结点进行交换,此时末尾就为最大值。
- 然后将剩余n-1个序列重新构造成一个堆,这样会得到n个元素中的次大值。如此反复执行,便能得到一个有序序列。
建堆和堆删除中都用到了向下调整,因此掌握了向下调整,就可以完成堆排序。
2.建堆
那我们到底怎么实现呢?
2.1向上调整建堆
很简单我们以建大堆为例
// 以下部分是向上调整建堆的代码,但已经被注释掉,因为通常使用向下调整建堆,效率更高 for (int i = 1; i < n; ++i) { // 对第i个元素执行向上调整操作,使其满足堆的性质 // 这种方式建堆的时间复杂度为O(N*logN),不是最优的 AdjustUp(a, i); }
2.2向上调整建堆和向下调整建堆时间复杂度
//向上调整建堆——O(N*logN)
for(int i=1;i<n;++i)
{
AdjustUp(a,i);
}
//向下调整建堆——O(N)
for(int i=(n-1-1)/2;i>=0;--i)
{
AdjustDown(a,n,i);
}2.3向下调整建堆
但是我们很快就会发现,这虽然可以,但是下面的堆调整排序用的是向下调整,我们这里如果使用向上调整,它的时间复杂度比向下调整的大,这会加大消耗,所以我们使用向下调整
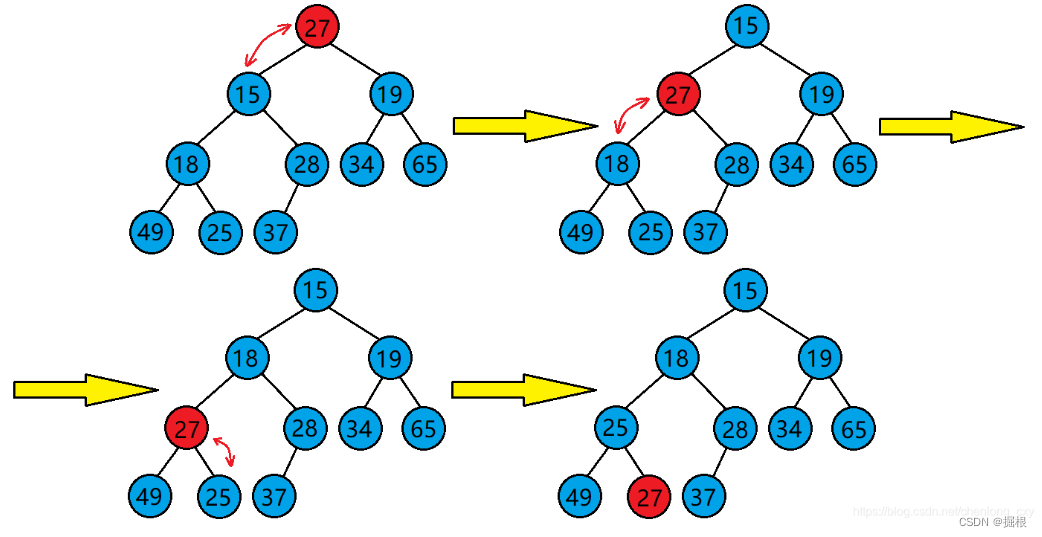
// 建堆 -- 向下调整建堆 -- O(N)
for (int i = (n - 1 - 1) / 2; i >= 0; --i)
{
AdjustDown(a, n, i);
}
2.4建什么堆
我们向排升序,我们建什么堆?降序呢?
我们以升序为例
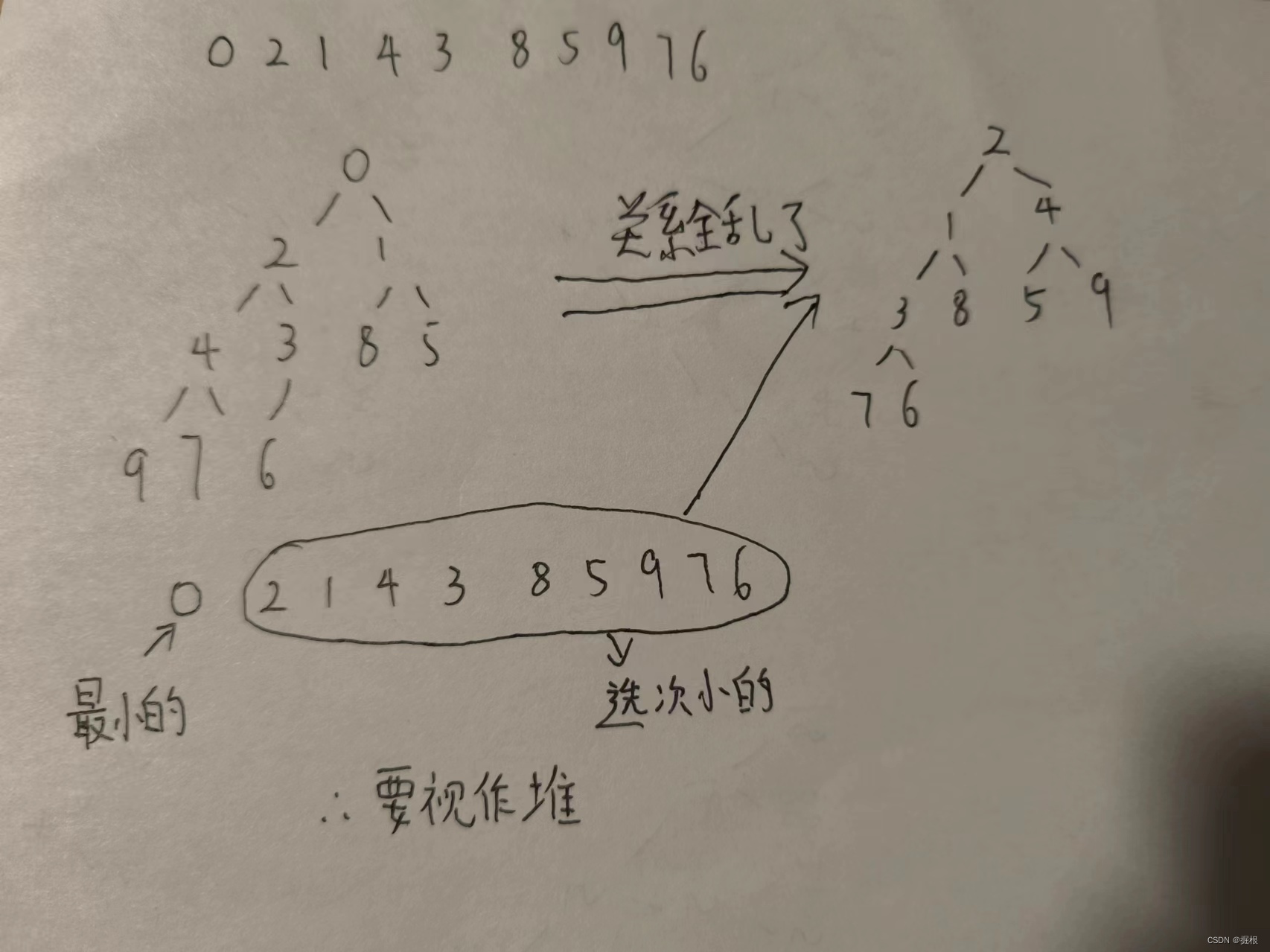
有人说升序建小堆,因为打印小堆的第一个元素最小嘛但是这样子看起来轻松,但是实际上真的轻松吗?
我们要选次小的,只能将除了根节点之外的其他元素视作一个堆,这样子后面的关系全乱了——原来的兄弟变父子了,父子变兄弟了,那就重新建堆了,时间复杂度O(N*logN),代价太大了
不如直接遍历选择O(logN)
所以我们升序建大堆,降序建小堆
3 .堆调整排序
- 此时整个序列的最大值(或最小值)就是堆顶的根结点。将其与末尾结点进行交换,此时末尾就为最大值(最小值)。
- 然后将剩余n-1个序列重新构造成一个堆,这样会得到n个元素中的次大(小)值。如此反复执行,便能得到一个有序序列。
简单的来说就是建堆得最大(小)值然后放到最后面去,对剩下的(除了放到后面去的)元素建堆选出最大(小)值,再放到后面去,再建堆,再放到后面去,依次类推
假设我们已经建好了一个大堆
int a[]={20,17,4,16,5,3};则堆排序应该是这样子的
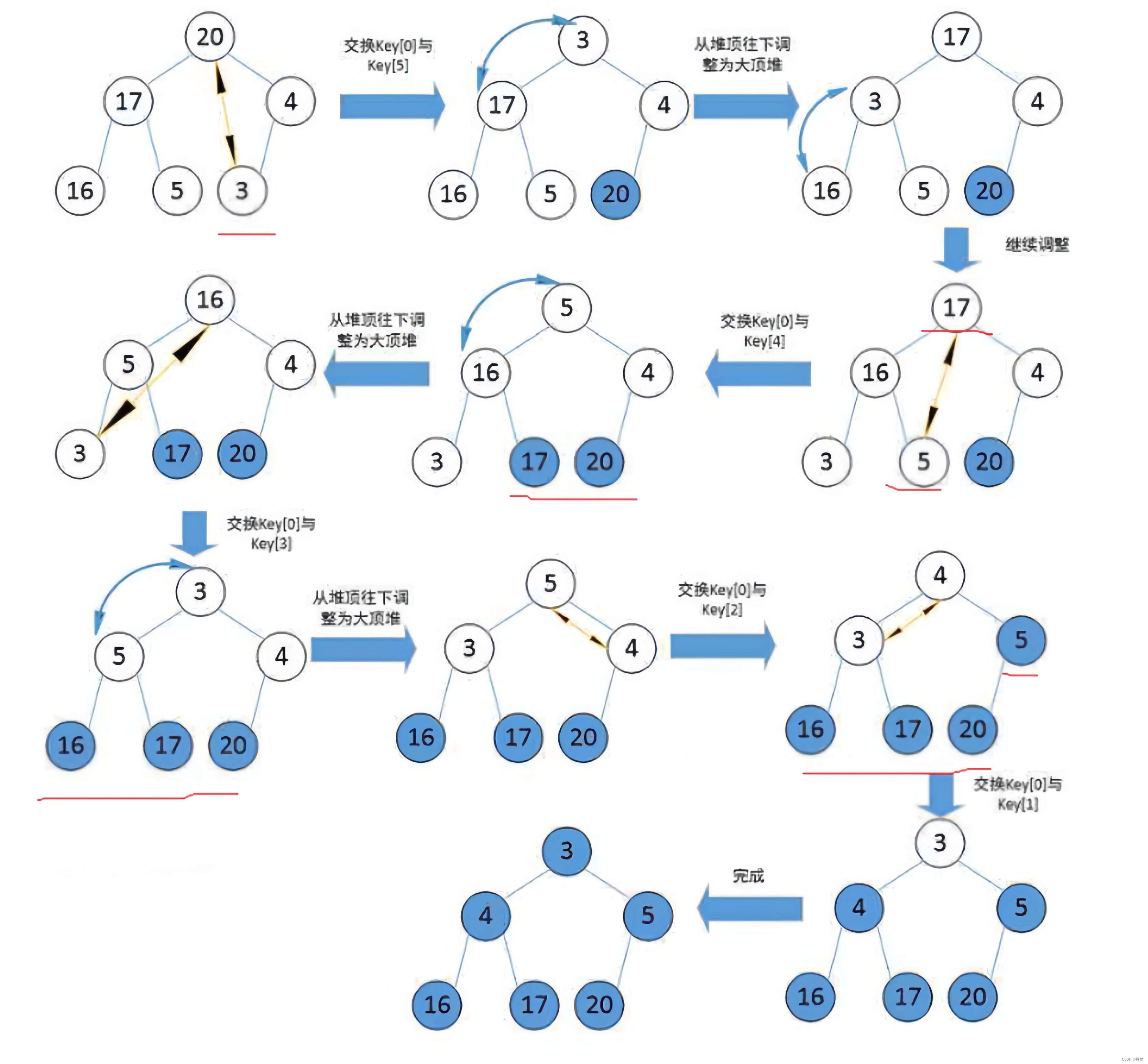
代码实现
int end = n - 1;
while (end > 0)
{
Swap(&a[end], &a[0]);
AdjustDown(a, end, 0);
--end;
}
4.堆排序代码实现
// HeapSort函数:使用堆排序算法对数组a进行升序排序
void HeapSort(int* a, int n)
{
// 使用向下调整建堆,从最后一个非叶子节点开始向前遍历
for (int i = (n - 1 - 1) / 2; i >= 0; --i)
{
// 对当前非叶子节点执行向下调整操作,使其及其子树满足堆的性质
// 由于每个非叶子节点只调整一次,因此总的时间复杂度为O(N)
AdjustDown(a, n, i);
}
// 以下部分是堆排序的主体,将堆顶的最大值(大顶堆)与当前未排序部分的最后一个元素交换
// 并重新调整堆,以保持堆的性质,直到整个数组排序完成
int end = n - 1; // end指向未排序部分的最后一个元素的索引
while (end > 0)
{
// 将堆顶元素(当前最大值)与未排序部分的最后一个元素交换
Swap(&a[end], &a[0]);
// 重新调整堆,保持堆的性质,此时堆的大小减少了1(因为已经取出了一个元素)
AdjustDown(a, end, 0);
// 缩小未排序部分的范围
--end;
}
}HeapSort 函数是用于执行堆排序的主要函数,它包括建堆和堆排序的两个主要步骤。
这里您选择使用向下调整的方法来建堆,这是一个高效的方法,因为向下调整每个非叶子结点只需要O(logN)的时间,并且整个建堆过程的时间复杂度为O(N)。所以整个堆排序过程的时间复杂度为O(N*logN)。
5.代码解释
建堆 -- 向下调整建堆 -- O(N)
for (int i = (n - 1 - 1) / 2; i >= 0; --i)
{
AdjustDown(a, n, i);
} 这段代码从最后一个非叶子结点开始,向前遍历到根结点,并对每个结点调用AdjustDown函数进行向下调整。
由于非叶子结点的索引是(n - 1) / 2(向下取整),这里(n - 1 - 1) / 2是为了得到正确的最后一个非叶子结点的索引。每个结点的向下调整时间复杂度为O(logN),但由于每个结点只调整一次,所以整个建堆过程的时间复杂度为O(N)。
堆排序 -- O(N*logN)
int end = n - 1;
while (end > 0)
{
Swap(&a[end], &a[0]);
AdjustDown(a, end, 0);
--end;
} 这部分代码执行堆排序的主体部分。
它首先将堆顶元素(即当前最大值)与数组的末尾元素交换,然后调整剩下的元素使其恢复为大顶堆的性质。这个过程反复进行,直到堆中只剩下一个元素为止。每次交换和调整的时间复杂度为O(logN),因为需要调整n-1次,所以整个堆排序过程的时间复杂度为O(N*logN)。
6.测试代码
#include<stdio.h>
typedef int HPDataType;
void Swap(HPDataType* p1, HPDataType* p2)
{
HPDataType x = *p1;
*p1 = *p2;
*p2 = x;
}
//堆的向下调整(大堆)
void AdjustDown(HPDataType* a, int n, int parent)
{
int child = parent * 2 + 1; // 计算左子节点的索引
// 当 child 索引在数组范围内时执行循环
while (child < n)
{
// 如果右子节点存在且大于左子节点
if (child + 1 < n && a[child + 1] > a[child])
{
++child; // 更新 child 为右子节点的索引
}
// 如果 child 节点(现在是左右子节点中较大的一个)大于 parent 节点
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]); // 交换 parent 和 child 的值
parent = child; // 更新 parent 为刚刚交换过的 child 的索引
child = parent * 2 + 1; // 重新计算左子节点的索引
}
else
{
break; // child 节点不大于 parent 节点,无需继续调整,退出循环
}
}
}
// HeapSort函数:使用堆排序算法对数组a进行升序排序
void HeapSort(int* a, int n)
{
// 使用向下调整建堆,从最后一个非叶子节点开始向前遍历
for (int i = (n - 1 - 1) / 2; i >= 0; --i)
{
// 对当前非叶子节点执行向下调整操作,使其及其子树满足堆的性质
// 由于每个非叶子节点只调整一次,因此总的时间复杂度为O(N)
AdjustDown(a, n, i);
}
// 以下部分是堆排序的主体,将堆顶的最大值(大顶堆)与当前未排序部分的最后一个元素交换
// 并重新调整堆,以保持堆的性质,直到整个数组排序完成
int end = n - 1; // end指向未排序部分的最后一个元素的索引
while (end > 0)
{
// 将堆顶元素(当前最大值)与未排序部分的最后一个元素交换
Swap(&a[end], &a[0]);
// 重新调整堆,保持堆的性质,此时堆的大小减少了1(因为已经取出了一个元素)
AdjustDown(a, end, 0);
// 缩小未排序部分的范围
--end;
}
}
int main()
{
int a[] = { 2,6,8,9,4,5,1,3,7 };
int size = sizeof(a) / sizeof(a[0]);
HeapSort(a, size);
for (int i = 0; i < size; i++)
{
printf("%d ", a[i]);
}
}
大家一定要注意:升序建大堆,降序建小堆