本文来源——b站忠厚老实的老王，链接：忠厚老实的老王投稿视频-忠厚老实的老王视频分享-哔哩哔哩视频 (bilibili.com)，侵删。
功率和转速之间的关系就是：功率P等于转矩M乘以转速ω。并不是油门越大加速度就越大。
发动机和电机的转速扭矩图对比：
电机的效率一般可以高达百分之九十，在高速区一般是遵循P=Fv的关系。
无人驾驶车辆一般在电车上面部署，这里只需要弄清楚电机的转速扭矩曲线即可，如下：
如上，电机在到达最大功率前，是以最大扭矩运行的，等转速到达最大功率之后，就以恒功率运行。按照这个特性可以造一段电机的转矩曲线（假设油门开度和功率是线性关系），如下：
上面的黑线对应的油门踩到底时对应转速——扭矩曲线，这里假设油门开度和功率是线性关系，也就是当油门是0.2开度时，对应的功率是380*0.2=76kw。
在2016.1版的carsim中没有电车车型，可以手动配置上面的电机参数，模拟出来一个电车，具体操作如下：
模型的输入是发动机的扭矩：
输出是汽车的纵向速度和加速度以及曲轴的转速：
变速器的设置如下：
设置如上，将传动比都设置成2，相当于没有变速器，将每个档位的转动惯量都设置成0.04，将每个档位的机械效率都设置成0.92。
道路设置如下：
刹车/油门标定表的制作（重点）
原理：给定一个恒定的油门，车跑起来会后，会输出一个速度和加速度。标定表就是找到油门和v、a之间的关系。
基于而言：
如上，thr是油门，就是踩不同的油门，就得到不同的速度和加速曲线，例如上面当油门开度是0.3时，速度和加速度曲线就可以画出来，速度和加速度可以合并到一个图上。一般来说速度和加速度曲线的一般趋势都是上图的趋势，也就是速度越高，加速度越差，因为P=Mω，速度很大时，力矩就会变小。
传统做实验的方法有几个缺点：①试验路面必须平直并且足够长；②方向盘不能动，但是在实际试验过程中方向盘不可能完全不动；③无法解决车辆在行驶过程中质量变换的问题。乘用车还不是很明显，但在装载货物的大货车上面空载和满载时的标定表不适配，需要在不用载荷时标定，比较繁琐。现在比较新兴的标定方法就是使用深度学习模型把v、a和质量作为特征进行训练深度学习在线进行更新，可以适应不同质量。下面使用传统的方法来制作标定表：
在carsim中设置输入\输出进行制作标定表：
由于要标定油门和刹车，所以输入是油门和刹车的制动压力。
simulink模型如下：
其中，thr是一个constant模块，将其使用thr参数，vx和ax是两个to workspace模块，可以将跑出来的结果导入的工作区中，这里首先标定油门，所以将刹车设置成0。
.m文件：
这里主要要将to workspace模块中模块属性取消勾选单一仿真输出，否则会报错。 取消方法：to workspace模块中消除out.前缀的方法：simulink->建模->模型设置->数据导入/导出->单一仿真输出取消勾选->点击应用确定
运行后，vx和ax等参数就传到了工作区：
其中table就是最终的标定表：
在2D-lookup table模块中进行如下设置：
加速度控制仿真框图如下：
加速度示波器中速度稳定在3一段时间后下降，这是因为电机特性，速度有限，不能再保持较高车速的情况下还有较大的加速度。
速度控制框图，设置期望速度是10，如下（如果控制效果不是很好，就吧油门标细一点）：
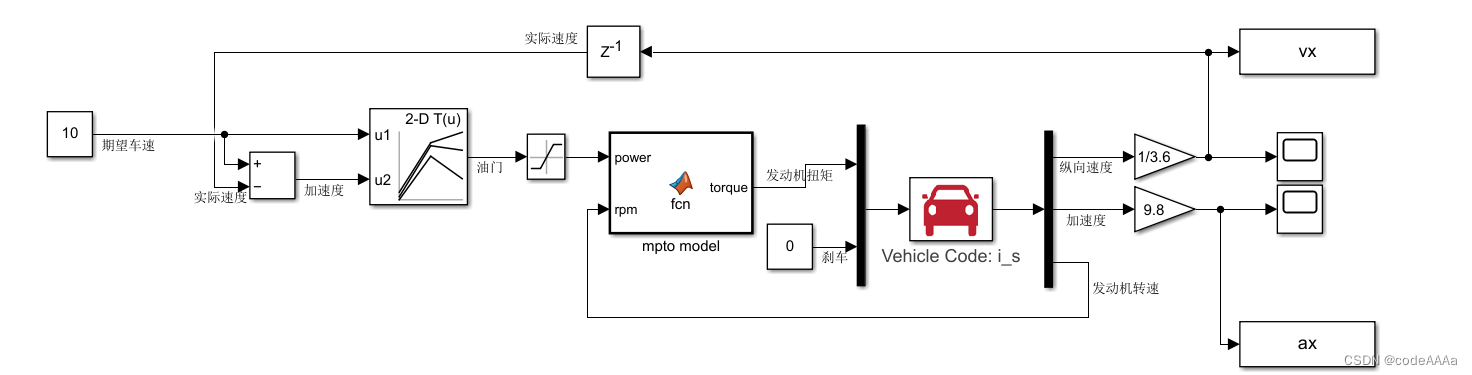
输出的速度信号的示波器图如下：
这里的加速度设置为期望的车速和实际车速的差值，将这个相减的结果输入到加速度信号中。加速度不能直接使用输出的加速度，因为加速度和速度要匹配，这里规划的速度是10，初速度是0，从0到10，刚开始必然要有一个很大的加速度，让车加速，后期加速度逐渐减小，最好的结果就是速度到10时，加速度刚好是0。如果直接使用车的实际加速度，这个实际的加速度并不一定和车速相匹配。下面演示直接使用实际加速度信号和将加速度信号设置成时:
可以看出当速度和加速不匹配时，跟踪速度的效果很差。相匹配的速度和加速度应该是当速度差距越大时，加速度越大，速度差距越小，加速度越小。直到速度到达期望速度时，加速度0。
刹车的标定表和油门标定表的制作方法相似：
标定的simulink系统框图：
首先在simulink中将油门设置成0，在carsim中将车辆的初速度设置为180km/h。
刹车标定代码：
标定表如下：
在第161列第一个数据对应的是加速度等于0，速度也等于0（坐标是（0,0）处于停车状态），但是此时拟合出来的制动压力很大为6点几，这是因为刹车的目的最后都是加速度为0，速度为0，所有曲线的焦点都是（0,0），这个坐标具有奇异性，这里matlab取了其平均值，这里对trabebr这个表做出修改，将这个坐标位置的刹车压力设置成0.3。
以-3减加速度控制：
加速度的示波器：
以0为期望速度的刹车控制系统框图：
加速度控制信号：
纵向双pid控制
首先将刹车和油门的标定表合并，将两者合并成一张标定表的好处就是控制时制动和油门会自动的控制平滑，不太会出现油门踩过了切换到刹车再切换到油门这样的不平顺的情况。合并一共需要三个m文件，前两个文件分别采集油门和刹车数据，油门和刹车的标定过程不能同时标定在一个m文件中，因为初速度不一样，油门的初速度是从0开始慢慢增大，刹车的初速度是从180或者144逐渐减小到0。第三个文件合并数据。
首先标定的模型框图：
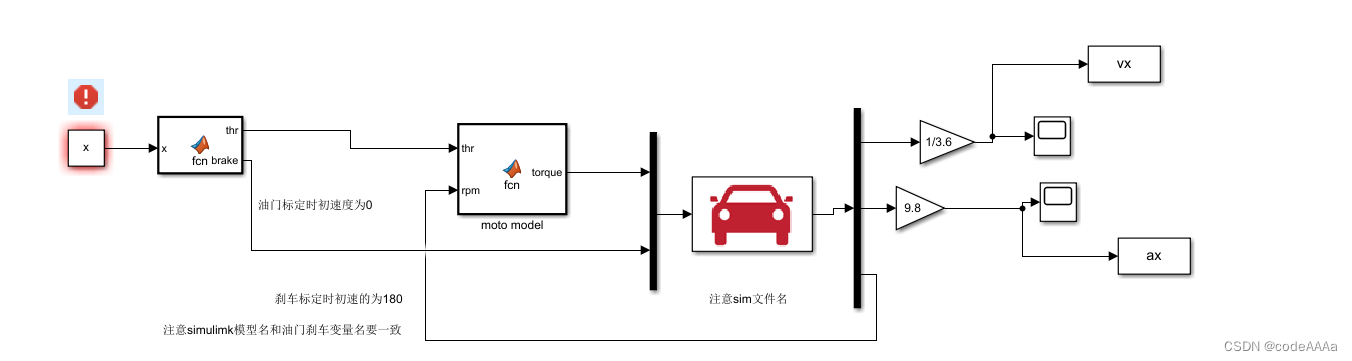
油门标定的代码：
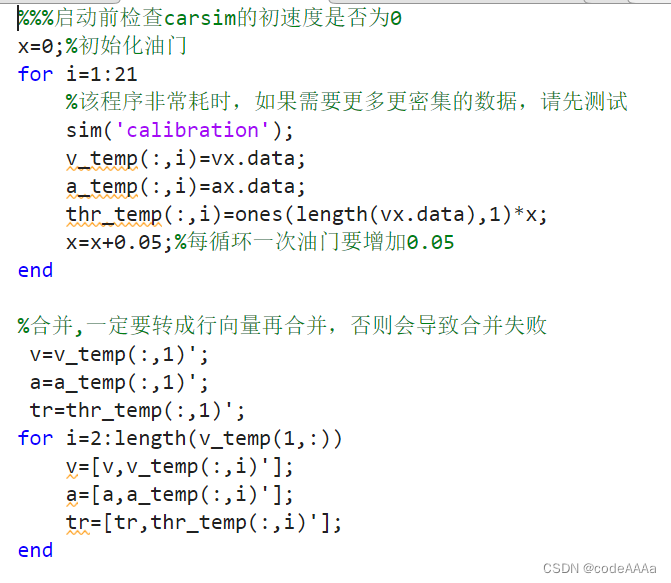
刹车标定的代码：
合并油门和刹车的代码：
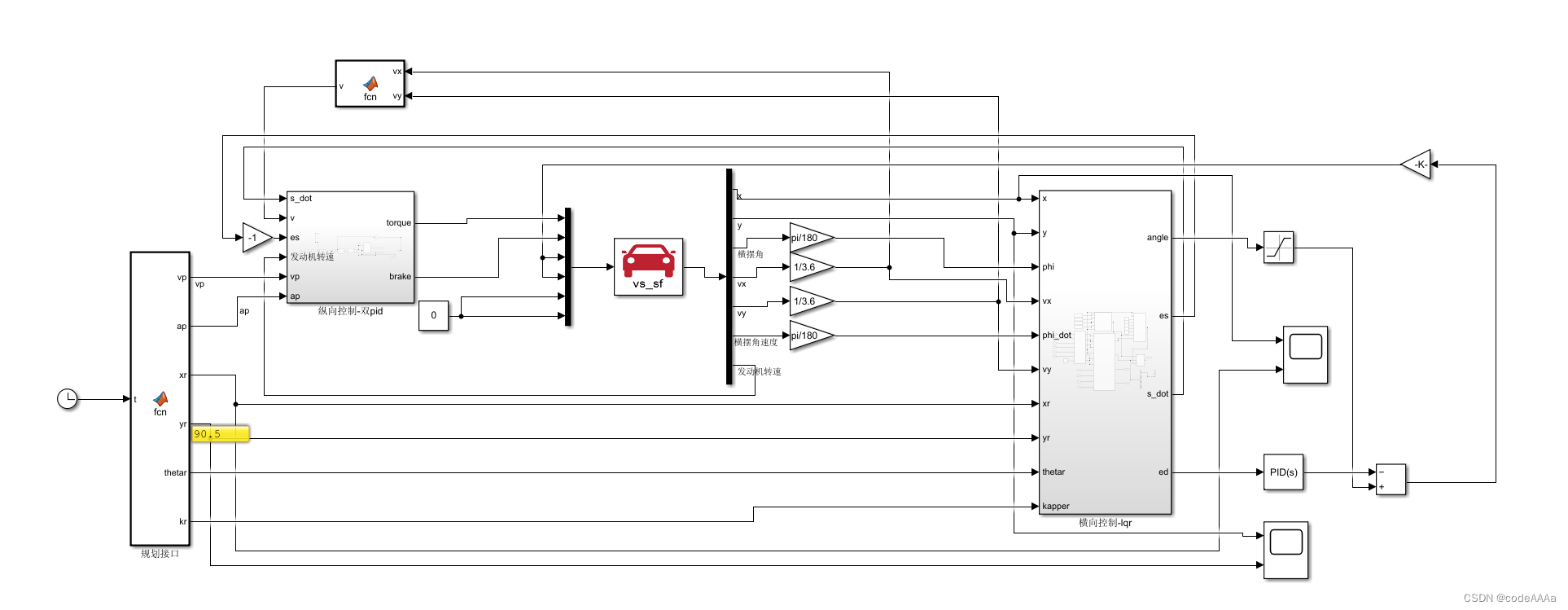
整体控制框图：
以10为期望速度，用10和当前速度相减可以得到加速度信号，这是一个简单的pid控制，也就是当当前速度距离期望速度很远时，有一个较大的加速度，距离很近时，加速度就比较小。这样可以基本可以实现对期望速度的控制，但是有稳态误差：
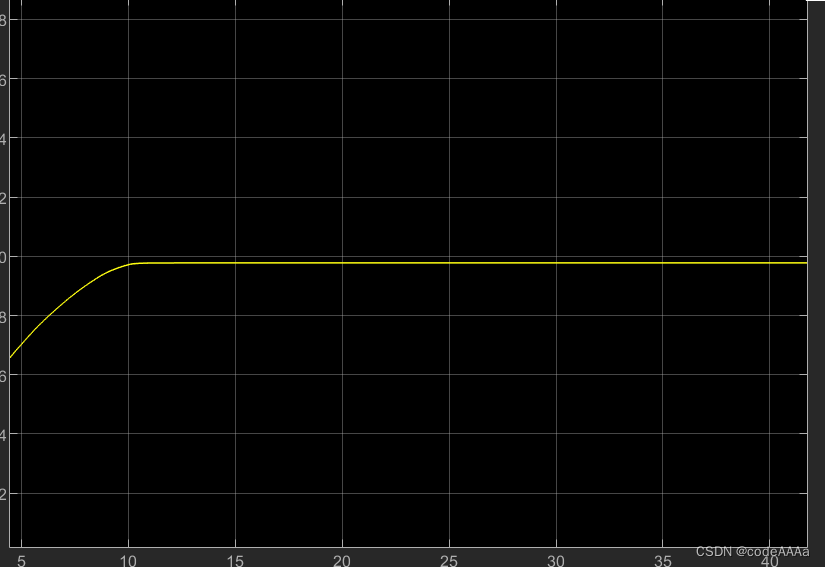
此时可以加一个比例增益也就是P控制，比例控制一般不能消除稳态误差，但是随着比例增益k的增加，控制输入量与误差成正比，同时k越大，系统的响应速度越快，稳态误差也会无限的接近于零，但在实际应用中比例系数不能无限增大。下面是当比例增益是10的输出情况，可以看出系统响应速度更快，也更接近于10，但是有明显振荡，这是因为比例增益增加了10倍，系统对误差更加敏感，稍微的误差就会引起响应，所以比例增益不是越大越好。
在carsim中将车辆的初速度设置为180km/h，使其减速到10m/s时的情况：
下面直接使用simulink中自带的pid模块，将比例增益设置为2，积分增益设为0.1，微分增益设置为0，此时输出会出现明显的超调，这是因为引入积分后会使得原来的一阶系统变成二阶系统，积分控制是可以消除稳态误差，只要实际速度和期望速度的差值不是0，积分随着时间的增长越来越大，所以只要时足够长，它一定可以收敛到期望值，如图：
微分控制中微分项与误差成正比，所以可以预测误差的变化趋势并提前做出反应，微分可以抑制超调，d控制也会增加系统的响应速度。
对d进行一下设置：
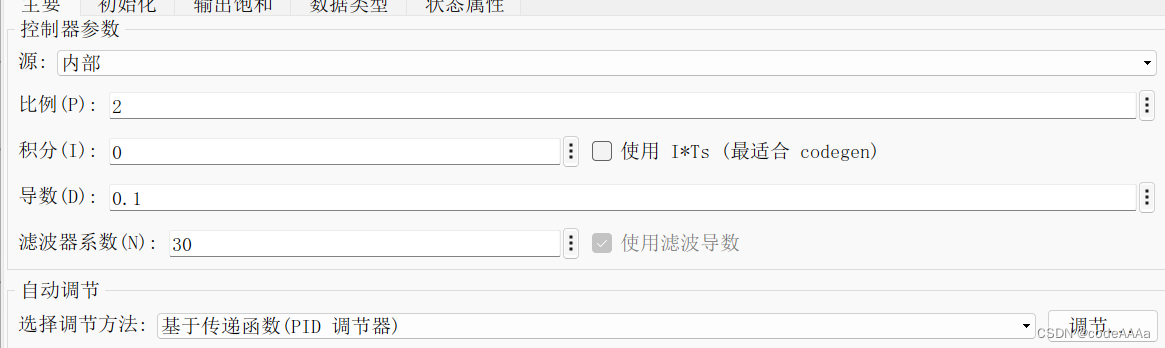
输出如下：
这里只用了比例微分控制，这里的比例项没有引起超调，所以对超调的控制效果不明显，但在实际应用中比例项是可以会引起超调，因为在实际应用中信号是有延迟的，下面可以加延迟模块模拟下实际应用的情况，假设油门和刹车信号到执行有100毫秒的延迟，速度从传感器出来有10ms的延迟。一般微分对比例带来的超调有较好的效果，但是微分对积分带来的超调效果不好，微分增益一般不能设置过大，过大会引起高频噪声。
模拟实际中的路径跟踪，框图如下：
自动驾驶横纵向控制总结：
轨迹规划是包含时间信息的，给定起点和终点的信息可以做很多场景，例如下面：
下面在绝对坐标系下规划，可以将问题转换成：
y是汽车横向方向，y的自变量是x，因为横向是由纵向引发的，但是只用y(x)来做轨迹规划是不够的，做轨迹规划的必须都是与时间相关的，所以要对y'（y对x进行求导）转换到y·（y对时间进行求导）进行转换。
现在就可以根据上面的边界边界条件以及时间T，规划出一条轨迹，生成x(t)、y(x)，在通过上面的转换关系算出y(t)。下面使用五次多项式，五次多项式对应由六个系数，正好对应着上面x的六个边界条件。对于y也一样。
路径的匹配点与时间相关，每过一个时间，规划器会发出一个规划的时间信息xr，yr、θr、kr。其中xr与yr就是规划器的xt与yt，与时间自然相关，θr、kr与时间产生关系如下：
规划使用大地坐标系，自然坐标系。
小结：规划到控制的逻辑
前4个公式是横向控制需要的；后面是纵向控制需要的，其中es和s·也是有横向中得来的，所以纵向控制的输入是3个。
路径规划算法接口：
需要注意的是这里的路径规划和之前横向控制的路径规划不一样，必须要算出每个轮子精确的侧偏刚度，这里知道精确的垂向力，然后根据不同的垂向力去查曲线再估算出侧偏刚度。
function [vp,ap,xr,yr,thetar,kr] = fcn(t)
dx=100;
dy=100;%dy为100，时间是50，为低速大转向工况
T=50;
% 初始和最终条件
xstart=[0,0,0];
xend=[dx,0,0];
ystart=[0,0,0];
yend=[dy,0,0];
% 计算 x(t)和y(t) 轨迹的系数,使用五次多项式
a=zeros(1,6);
b=zeros(1,6);
a(1)=xstart(1);
a(2)=xstart(2);
a(3)=xstart(3)/2;
A1=[T^3,T^4,T^5;
3*T^2,4*T^3,5*T^4;
6*T,12*T^2,20*T^3];
B1=[xend(1)-a(1)-a(2)*T-a(3)*T^2;
xend(2)-a(2)-2*a(3)*T;
xend(3)-2*a(3)];
xs=inv(A1)*B1;
a(4)=xs(1);
a(5)=xs(2);
a(6)=xs(3);
b(1)=ystart(1);
b(2)=ystart(2);
b(3)=ystart(3)/2;
A2=[dx^3,dx^4,dx^5;
3*dx^2,4*dx^3,5*dx^4;
6*dx,12*dx^2,20*dx^3];
B2=[yend(1)-b(1)-b(2)*dx-b(3)*dx^2;
yend(2)-b(2)-2*b(3)*dx;
yend(3)-2*b(3)];
ys=inv(A2)*B2;
b(4)=ys(1);
b(5)=ys(2);
b(6)=ys(3);
% 在时间 t 处计算位置 (xr, yr)
xr=a(1)+a(2)*t+a(3)*t^2+a(4)*t^3+a(5)*t^4+a(6)*t^5;
yr=b(1)+b(2)*xr+b(3)*xr^2+b(4)*xr^3+b(5)*xr^4+b(6)*xr^5;
% 一阶导数 (速度)
xr_dot=a(2)+2*a(3)*t+3*a(4)*t^2+4*a(5)*t^3+5*a(6)*t^4;
yr_dx=b(2)+2*b(3)*xr+3*b(4)*xr^2+4*b(5)*xr^3+5*b(6)*xr^4;
yr_dot=yr_dx*xr_dot;
% 方向角度 (thetar)
thetar=atan(yr_dx);
xr_dot2=2*a(3)+6*a(4)*t+12*a(5)*t^2+20*a(6)*t^3;
yr_dx2=2*b(3)+6*b(4)*xr+12*b(5)*xr^2+20*b(6)*xr^3;
yr_dot2=yr_dx2*xr_dot^2+yr_dx*xr_dot2;
kr=yr_dx2/((1+yr_dx^2)^1.5);
% 计算速度 (vp) 和加速度 (ap)
vp=sqrt(xr_dot^2+yr_dot^2);
if xr_dot2>=0 %ap可正可负，在加速时是正的，减速时是负的。
ap=sqrt(xr_dot2^2+yr_dot2^2);
else
ap=-sqrt(xr_dot2^2+yr_dot2^2);
end仿真框图：
在低速打转向时的跟踪效果：
在低速大转向时跟踪效果良好。
在平时搭建模型跑出得结果中横向误差很大时，大概率原因如下：（1）不足转向（2）调解LQR，或者调节权重矩阵Q调大，给ed一个较大的惩罚值，但是也不能太大，太大会引起超调。（3）将轮胎的侧偏刚度估计地准一些。
下面演示如果调节因为转向不足引起得横向误差过大。
汽车有不足转向的原因：
处理方法：对横向误差使用pid的积分模块，对横向误差进行积分，将误差积分补偿到计算出的角度（计算出来的转角减去误差积分）。理解为，angle是向左为正，ed也是向左为正，当横向误差ed是正值时，相当于向左打多了，此时减去它相当于往右回正了一点。
修改后的模型框图：
