[Collection与数据结构] Map与Set(一):二叉搜索树与Map,Set的使用

news2024/12/25 8:51:56

🌸个人主页:https://blog.csdn.net/2301_80050796?spm=1000.2115.3001.5343
🏵️热门专栏:🍕 Collection与数据结构 (91平均质量分)https://blog.csdn.net/2301_80050796/category_12621348.html?spm=1001.2014.3001.5482
🧀Java EE(94平均质量分) https://blog.csdn.net/2301_80050796/category_12643370.html?spm=1001.2014.3001.5482
🍭MySql数据库(93平均质量分)https://blog.csdn.net/2301_80050796/category_12629890.html?spm=1001.2014.3001.5482
感谢点赞与关注~~~
在这里插入图片描述

目录

  • 1. 搜索树
    • 1.1 概念
    • 1.2 查找结点
    • 1.3 插入结点
    • 1.4 删除结点(难点)
    • 1.5 实现二叉搜索树
    • 1.6 性能分析
    • 1.7 和Java中Collection的关系
  • 2. Map和Set
    • 2.1 概念与场景
    • 2.2 两种模型
    • 2.3 Map的使用
      • 2.3.1 关于Map的说明
      • 2.3.2 关于Map.Entry<K,V>的说明
      • 2.3.3 常用方法
    • 2.4 Set的使用
      • 2.4.1 常用方法

1. 搜索树

1.1 概念

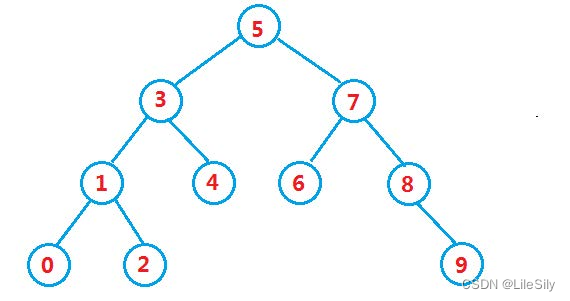
二叉搜索树又称为二叉排序树,它可以是一颗空树,或者是具有以下性质的二叉树.

  • 若他的右树不为空,则它的右子树上的所有结点都大于根结点.
  • 若它的左树不为空,则它的左子树上的所有结点都小于根结点.
  • 它的左子树和右子树也分别为二叉搜索树.
    在这里插入图片描述

1.2 查找结点

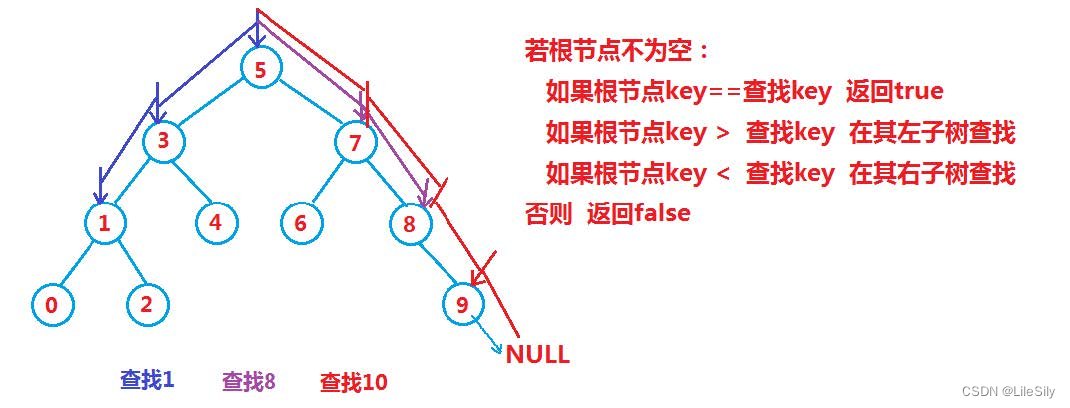
如果根节点为空,返回false.如果根结点不为空:

  • 如果根结点key == 查找key,返回true.
  • 如果根结点key < 查找key,到其右子树中查找.
  • 如果根结点key > 查找key,到其左子树中查找.
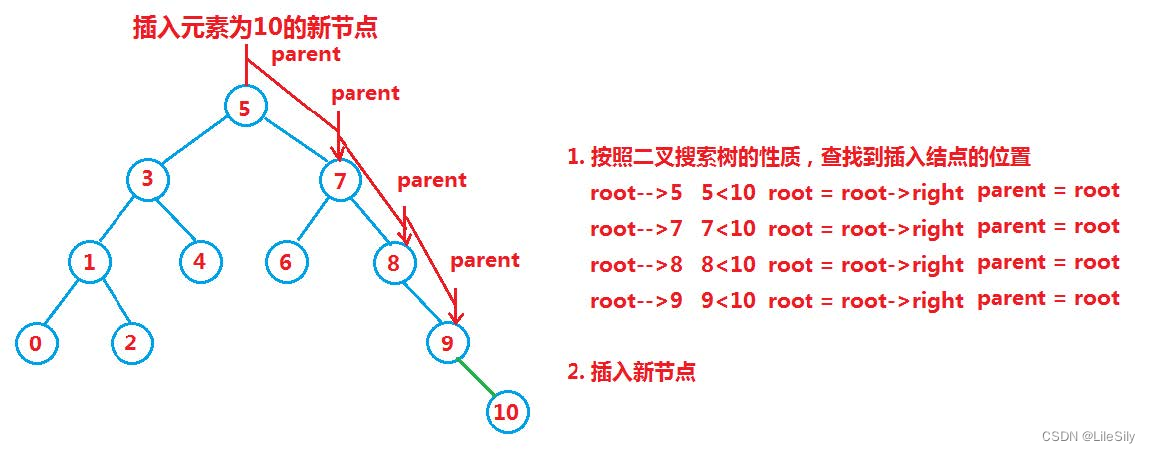
    在这里插入图片描述

1.3 插入结点

  • 如果为空树,直接令root = 所要插入的结点.之后返回true.
    在这里插入图片描述
  • 如果该树不是空树,按照搜索二叉树的性质确定查找逻辑.插入新结点.注意记录cur的父节点,否则无法插入.
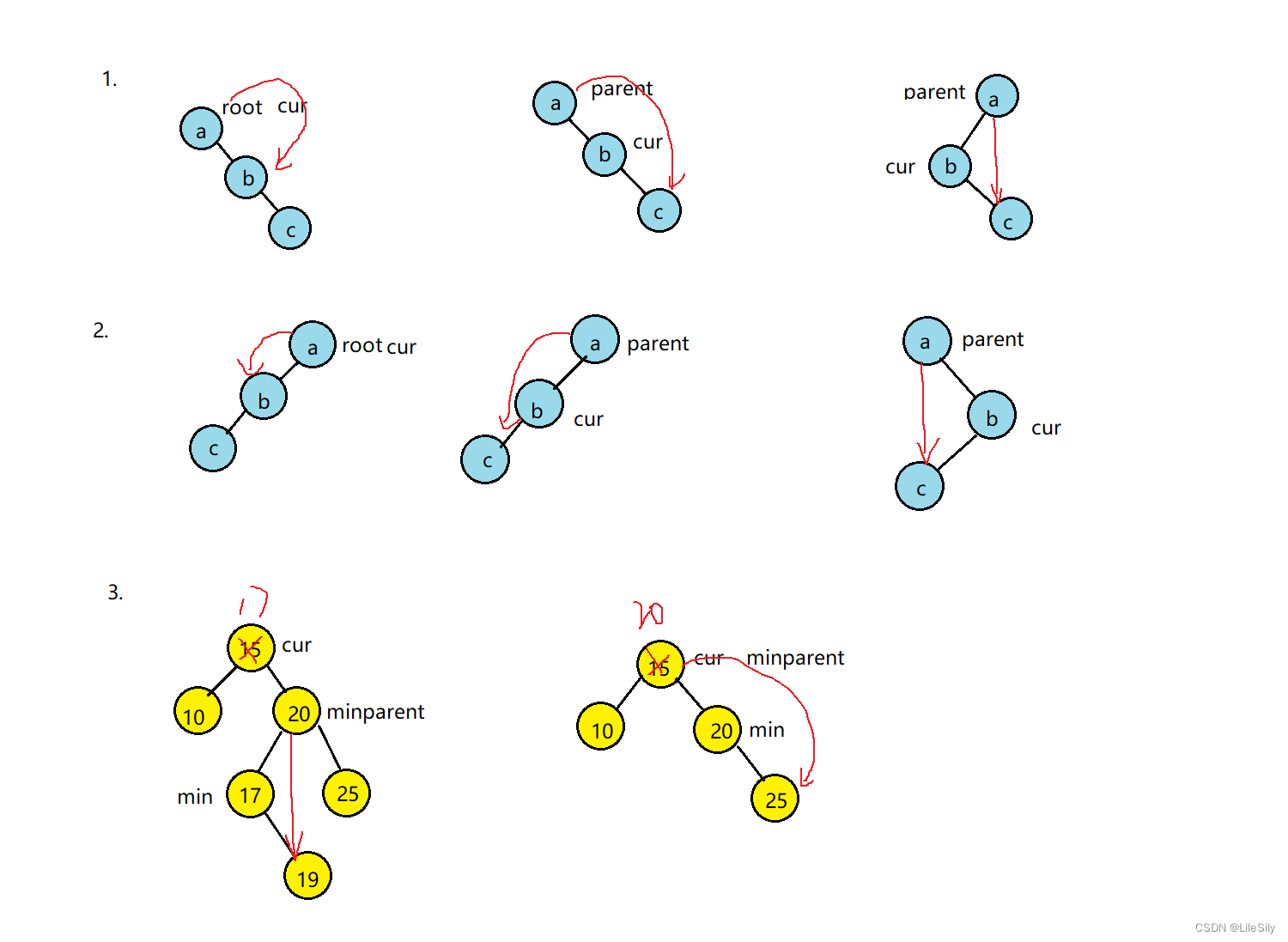
    在这里插入图片描述

1.4 删除结点(难点)

设待删除的结点是cur,带删除的结点的父节点是parent.

  1. cur的左子树为空
    • 要删除的节点是根结点,直接令root = root.right
    • 要删除的结点是中间的结点, 单分支,parent.right = cur.right
    • 要删除的结点是中间结点,<字型,parent.left = cur.right
  2. cur的右子树为空
    • 要删除的结点是根结点,直接令root = root.left
    • 要删除的结点是中间结点,单分支,parent.left = cur.left
    • 要删除的结点是中间结点,>字型,parent.right = cur.left
  3. cur的左右子树都不为空
    可以使用替换法进行删除,即它在右子树中寻找最小的结点,或者在左子树中寻找最大的结点,使用找到的结点替换要删除的结点,然后删除找到的最小(大)的结点,之后又分为两种情况(以右子树为例):
    • 最小的结点与上下的结点组成<型.
    • 最小的结点与上下结点形成单分支.
      [图解]
      在这里插入图片描述

1.5 实现二叉搜索树

public class SearchBinaryTree {
    //搜索树的结点
    public static class Node{
       public int key;
       public Node left;
       public Node right;

        public Node(int key) {
            this.key = key;
        }
    }
    private Node root = null;

    /**
     * 查找元素
     * @param key 索要查找的元素
     * @return 返回Node的哈希值
     */
    public Node search(int key){
        Node cur = root;
        while (cur != null){
            if (cur.key == key){
                return cur;
            } else if (cur.key < key) {
                cur = cur.right;
            }else {
                cur = cur.left;
            }
        }
        return null;//没找到,返回null
    }

    /**
     * 在二叉搜索树中插入指定的值
     * @param key 所要插入的值
     * @return 返回是否插入成功
     */
    public boolean insert(int key){
        Node node = new Node(key);
        Node cur = root;
        Node parent = null;
        if (root == null){
            root = node;
            return true;
        }
        while (cur != null){
            if (cur.key == key){
                return false;//二叉搜索树中不允许有两个相同的值,遇到相等返回false
            } else if (cur.key < key) {
                parent = cur;
                cur = cur.right;
            }else {
                parent = cur;
                cur = cur.left;
            }
        }
        //退出循环后,判断结点应该插入在左侧还是右侧
        if (parent.key < key){
            parent.right = node;
        }else {
            parent.left = node;
        }
        return true;
    }

    /**
     * 删除指定值的结点
     * @param key 所要删除的值
     * @return 返回是否删除成功
     */
    public boolean remove(int key){
        Node cur = root;
        Node parent = null;
        if (root == null){
            return false;
        }
        while (cur != null){
            if (cur.key == key){
                removeNode(parent,cur);
                return true;
            } else if (cur.key < key) {
                parent = cur;
                cur = cur.right;
            }else {
                parent = cur;
                cur = cur.left;
            }
        }
        return false;//没找到,返回false
    }

    /**
     * 找到结点之后删除
     * @param parent 父结点
     * @param cur 当前要删除的结点
     */
    private void removeNode(Node parent,Node cur){
        if (cur.left == null){//cur的左结点为空
            if (cur == root){//当前要删除的结点是根结点
                root = root.right;
            } else if (parent.right == cur) {//删除的是单分支的中间节点
                parent.right = cur.right;
            }else {//删除的是<字型的中间结点
                parent.left = cur.right;
            }
        } else if (cur.right == null) {//cur的右结点为空
            if (cur == root){//当前要删除的结点是根结点
                root = root.left;
            } else if (parent.left == cur) {//删除的是单分支的中间节点
                parent.left = cur.left;
            }else {//删除的是>字型的中间结点
                parent.right = cur.left;
            }
        }else {//左右结点都不为空,使用替换删除法
            //在这个结点的右子树中寻找最小的值,用它进行替换,原因:这样右结点的值一定比替换之后的值大
            Node t = cur.right;
            Node tparent = cur;
            //寻找右子树的最小结点,一直向左子树遍历,因为只有左结点的值才比根结点小,
            while (t.left != null){//当没有左结点的时候停止遍历
                tparent = t;
                t = t.left;
            }
            cur.key = t.key;
            //删除替换掉的结点
            if (tparent.left == t){//<字型
                tparent.left = t.right;
            }else {//单分支型
                tparent.right = t.right;
            }
        }
    }
}

1.6 性能分析

插入和删除操作都必须先查找，查找效率代表了二叉搜索树中各个操作的性能。
对有n个结点的二叉搜索树，若每个元素查找的概率相等，则二叉搜索树平均查找长度是结点在二叉搜索树的深度的函数，即结点越深，则比较次数越多。
但对于同一个关键码集合，如果各关键码插入的次序不同，可能得到不同结构的二叉搜索树：
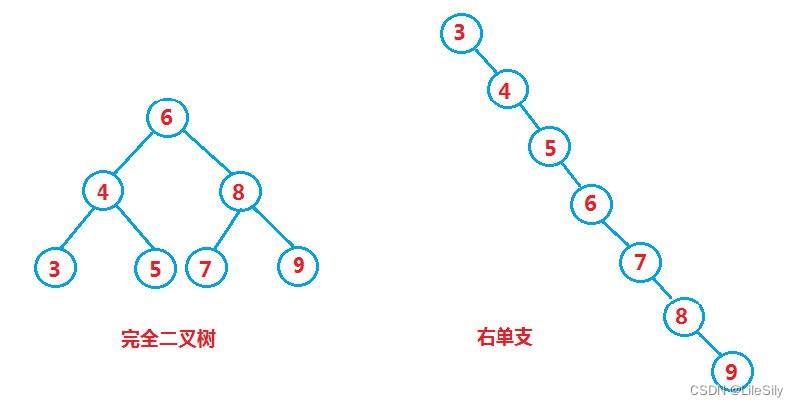
在这里插入图片描述
最优情况下，二叉搜索树为完全二叉树，其平均比较次数为：log2N
最差情况下，二叉搜索树退化为单支树，其平均比较次数为：N/2

1.7 和Java中Collection的关系

TreeMap 和 TreeSet 即 java 中利用搜索树实现的 Map 和 Set；实际上用的是红黑树，而红黑树是一棵近似平衡的二叉搜索树，即在二叉搜索树的基础之上 + 颜色以及红黑树性质验证，关于红黑树的内容后序再进行讲解。

2. Map和Set

2.1 概念与场景

Map和Set是一种专门用来就那些搜索的容器或者数据结构,其搜索的效率与它们具体的例子有关.
以前常见的搜索方式有：
1. 直接遍历，时间复杂度为O(N)，元素如果比较多效率会非常慢
2. 二分查找，时间复杂度为 ,但搜索前必须要求序列是有序的
上述排序比较适合静态类型的查找，即一般不会对区间进行插入和删除操作了，而现实中的查找比如：
1. 根据姓名查询考试成绩
2. 通讯录，即根据姓名查询联系方式
3. 不重复集合，即需要先搜索关键字是否已经在集合中
可能在查找时进行一些插入和删除的操作，即动态查找，那上述两种方式就不太适合了，本节介绍的Map和Set是一种适合动态查找的集合容器。

2.2 两种模型

一般把搜索的数据称为关键字(key),和关键字对应的值称为值(value),将其称为key-value键值对,所以会有两种模型.

  1. 纯key模型,容器中只存了key一个值.
  2. key-value模型,容器中存的是key-value的键值对.
    Map中存储的是key-value键值对(有点类似于python中的字典),Set中只存储了key(有点类似于python中的集合).

2.3 Map的使用

2.3.1 关于Map的说明

Map是一个接口类，该类没有继承自Collection，该类中存储的是<K,V>结构的键值对，并且K一定是唯一的，不能重复.

2.3.2 关于Map.Entry<K,V>的说明

Map.Entry<K,V>是Map内部实现的内部类,用来表示Map中Key于Value的映射关系(类似于python字典中的items),该内部类中主要提供了key和value的获取方式,以及value的设置.

方法解释
K getKey()返回 entry 中的 key
V getValue()返回 entry 中的 value
V setValue(V value)将键值对中的value替换为指定value

[注意]
在Map.Entry<K,V>类中没有提供key的设置方法,即该类中的key一旦确定就不可更改.

2.3.3 常用方法

方法解释
V get(Object key)返回 key 对应的 value
V getOrDefault(Object key, V defaultValue)返回 key 对应的 value，key 不存在，返回默认值
V put(K key, V value)设置 key 对应的 value
V remove(Object key)删除 key 对应的映射关系
Set<K> keySet()返回所有 key 的不重复集合(Map中的key不可重复)
Collection<V> values()返回所有 value 的可重复集合(Map中的value可重复)
Set<Map.Entry<K, V>> entrySet()返回所有的 key-value 映射关系
boolean containsKey(Object key)判断是否包含 key
boolean containsValue(Object value)判断是否包含 value

[注意事项]

  1. Map是一个接口，不能直接实例化对象，如果要实例化对象只能实例化其实现类TreeMap或者HashMap
  2. Map中存放键值对的Key是唯一的，value是可以重复的
  3. 在TreeMap中插入键值对时，key不能为空，否则就会抛NullPointerException异常，value可以为空。但是HashMap的key和value都可以为空。
  4. Map中的Key可以全部分离出来，存储到Set中来进行访问(因为Key不能重复)。
  5. Map中的value可以全部分离出来，存储在Collection的任何一个子集合中(value可能有重复)。
  6. Map中键值对的Key不能直接修改，value可以修改，如果要修改key，只能先将该key删除掉，然后再来进行重新插入。
  7. TreeMap的底层结构是红黑树,增删查改的时间复杂度是log2N,HashMap的底层结构是哈希桶.时间复杂度是1,哈希桶直接可以根据索引找到位置,不需要遍历.
  8. TreeMap和HashMap的线程都不安全.

使用实例:

import java.util.Map;
import java.util.Set;
import java.util.TreeMap;

public class Main {
    public static void main(String[] args) {
        Map<Integer,String> map = new TreeMap<>();
        map.put(1,"一");//添加元素
        map.put(2,"二");
        map.put(3,"三");
        map.put(4,"四");
        map.put(5,"五");
        System.out.println(map.size());//打印map大小
        System.out.println(map.get(5));//获取5对应的value
        System.out.println(map.getOrDefault(6,"不存在"));//6不存在,返回默认值
        map.remove(5);//删除5对应的键值对
        Set<Integer>set = map.keySet();//拿到map的key集合
        for(int x:set){
            System.out.print(x+" ");
        }
        for (String x:map.values()){
            System.out.println(x+" ");
        }
        Set<Map.Entry<Integer,String>> set1 = map.entrySet();
        for (Map.Entry<Integer,String> x:set1){//把一个不可迭代的对象转换为可迭代对象,经常用
            System.out.println("key:"+x.getKey()+" "+"value:"+x.getValue());
        }
        System.out.println(map.containsKey(1));
        System.out.println(map.containsKey(6));
        System.out.println(map.containsValue("一"));
        System.out.println(map.containsValue("六"));
    }
}

运行结果:
在这里插入图片描述

2.4 Set的使用

Set和Map最主要的区别有两点:

  • Set继承于Collection接口,而Map没有,所以Set可以遍历,Map不可以遍历.
  • Set中只存储key,而Map中存的是key-value的键值对.

2.4.1 常用方法

方法解释
boolean add(E e)添加元素，但重复元素不会被添加成功
void clear()清空集合
boolean contains(Object o)判断 o 是否在集合中
Iterator<E> iterator()返回迭代器
boolean remove(Object o)删除集合中的 o
int size()返回set中元素的个数
boolean isEmpty()检测set是否为空，空返回true，否则返回false
Object[] toArray()将set中的元素转换为数组返回
boolean containsAll(Collection<?> c)集合c中的元素是否在set中全部存在，是返回true，否则返回false
boolean addAll(Collection<? extends E> c)将集合c中的元素添加到set中，可以达到去重的效果

[注意事项]

  1. Set是继承自Collection的一个接口类,所以是可遍历的对象.
  2. Set中只存储了key，并且要求key一定要唯一.
  3. TreeSet的底层是使用Map来实现的，其使用key与Object的一个默认对象作为键值对插入到Map中的
  4. Set最大的功能就是对集合中的元素进行去重
  5. 实现Set接口的常用类有TreeSet和HashSet，还有一个LinkedHashSet，LinkedHashSet是在HashSet的基础上维护了一个双向链表来记录元素的插入次序。
  6. Set中的Key不能修改(这里与python不同.python中的集合是可变的)，如果要修改，先将原来的删除掉，然后再重新插入
  7. TreeSet中不能插入null的key，HashSet可以.

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1657433.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

程序设计——前后端分离实现简单表白墙

程序设计——前后端分离实现简单表白墙

文章目录 一、前端页面样式代码二、前后端衔接1. 后端创建 maven 项目2. 针对前后端交互的解释以及后端代码的实现针对 post 请求解释前后端衔接针对 Get 请求解释前后端衔接 3.后端与数据库的联系以及对数据的存取单独封装数据库连接代码解释后端存储 save 数据的代码解释后端…
阅读更多...
【因特网中自治系统内部的路由选择,RIP 进程处理 OSPFOSPF(Open Shortest Path First)最短路径优先协议】

【因特网中自治系统内部的路由选择,RIP 进程处理 OSPFOSPF(Open Shortest Path First)最短路径优先协议】

文章目录 因特网中自治系统内部的路由选择RIP&#xff08;Routing Information Protocol&#xff09;内部网关协议RIP通告&#xff08;advertisements&#xff09;RIP: 链路失效和恢复RIP 进程处理OSPF(Open Shortest Path First)最短路径优先协议OSPF “高级” 特性(在RIP中的…
阅读更多...
吴恩达机器学习笔记 三十七 电影推荐系统 使用特征 成本函数 协同过滤算法

吴恩达机器学习笔记 三十七 电影推荐系统 使用特征 成本函数 协同过滤算法

以电影评分系统为例&#xff0c;令 r(i, j) 来表示用户 j 已经对电影 i 评分&#xff0c; y&#xff08;i, j&#xff09;表示评分具体是多少。 假如每部电影有自己的特征&#xff0c;那么用户 j 对电影 i 的评分预测为 w(j) * x(i) b(j) r(i, j) &#xff1a;一个用户 j 是否…
阅读更多...
mysql: docker 异常 - mbind: Operation not permitted

mysql: docker 异常 - mbind: Operation not permitted

mbind: Operation not permitted 前言&#xff1a;正文:结论 &#xff1a; 前言&#xff1a; 用数据库处理平台问题今天报错&#xff0c;mbind: Operation not permitted。 mbind 不允许操作&#xff0c;一头雾水这是什么意思。 网上找了很多资料大概意思是&#xff1a; 这个错…
阅读更多...
MATLAB 点云随机赋色 （68）

MATLAB 点云随机赋色 （68）

MATLAB 点云随机赋色 （68） 一、算法介绍二、算法介绍1.代码2.结果三、数据链接一、算法介绍 读取的点云本身带有颜色信息，有时我们需要为每个点随机赋予一种颜色，下面是具体效果和实现代码，以及使用的数据： 二、算法介绍 1.代码 代码如下（示例）： % 读取点云文件 f…
阅读更多...
Windows如何安装hadoop

Windows如何安装hadoop

var code "da0f4508-813e-4f6c-b5e8-6c19f92be6d1"Hadoop是一个开源的分布式计算平台&#xff0c;旨在处理大规模数据的存储和处理。它提供了分布式文件系统&#xff08;HDFS&#xff09;和分布式计算框架&#xff08;MapReduce&#xff09;&#xff0c;使得用户能够…
阅读更多...
12 华三的二层链路聚合

12 华三的二层链路聚合

12 华三的二层链路聚合 配置思路 1. 配置二层静态聚合组 (1) 进入系统视图。 system-view (2) 创建二层聚合接口&#xff0c;并进入二层聚合接口视图。 interface bridge-aggregation interface-number [ lite ] 创建二层聚合接口后&#xff0c;系统将自动生成…
阅读更多...
Windows系统下修改文件夹和U盘图标实战

Windows系统下修改文件夹和U盘图标实战

文章目录 知识学习一、修改磁盘图标第一步、新建.INF文件第二步、放置图标第三步、重新插入U盘第四步、隐藏与显示文件知识拓展 二、修改文件夹图标设置图标样式恢复图标样式 在日常办公中使用的是windows系统&#xff0c;系统默认的文件图标都一样&#xff0c;不利于分类整理&…
阅读更多...
使用Python Pandas实现两表对应列相加（即使表头不同）

使用Python Pandas实现两表对应列相加（即使表头不同）

目录 引言 Pandas库简介 实现对应列相加 步骤一&#xff1a;加载数据 步骤二&#xff1a;重命名列 步骤三&#xff1a;对应列相加 步骤四&#xff1a;保存结果 案例分析 结论 引言 在数据分析和处理的日常工作中&#xff0c;我们经常会遇到需要将来自不同数据源的数据…
阅读更多...
拼多多投产比怎么逐步调高

拼多多投产比怎么逐步调高

提高拼多多的投产比&#xff08;ROI&#xff09;需要综合考虑多个因素&#xff0c;包括点击量、转化率、客单价以及点击花费。以下是一些有效的方法&#xff1a; 拼多多推广可以使用3an推客。3an推客&#xff08;CPS模式&#xff09;给商家提供的营销工具&#xff0c;由商家自…
阅读更多...
DDD领域驱动模型设计

DDD领域驱动模型设计

醍醐灌顶了朋友们 第一次写ddd还是 一路走来 丢失了东西 现在倒是也能找回来 只是有点可惜了 选择比努力更重要 独立功能 应用层&#xff1a;组织业务逻辑 领域&#xff1a;实体对象领域&#xff0c;业务核心 数据仓库&#xff1a; 不影响业务封装了数据操作&#xff0c;…
阅读更多...
惊人的视力恢复眼球操

惊人的视力恢复眼球操

阅读更多...
语义分割 之 YOLOv8的 train和predict参数详解

语义分割 之 YOLOv8的 train和predict参数详解

train 参数 predict 参数
阅读更多...
视频号小店为什么这么火呢？这个项目有哪些优点？

视频号小店为什么这么火呢？这个项目有哪些优点？

大家好&#xff0c;我是电商小V 今天可以说又爆火了一个电商项目&#xff0c;也是吸引了很多创业小伙伴的目光&#xff0c;你猜的没错&#xff0c;这个项目就是“视频号小店”&#xff0c;一度被认为是今年的风口期项目&#xff0c; 前几天在外面吃饭的时候&#xff0c;听到隔壁…
阅读更多...
车载测试系列：入行车载测试分享

车载测试系列：入行车载测试分享

车载测试前景如何&#xff1f; 软件定义汽车时代的发展趋势&#xff0c;随着控制器自主开发力度的加强&#xff0c;作为V流程中必备环节&#xff0c;车载测试工程师岗位需求会越来越多&#xff1b;控制器集成化&#xff0c;功能集成程度越来越高&#xff0c;对于测试工程师的知…
阅读更多...
linux中进程相关概念（一）

linux中进程相关概念（一）

什么是程序&#xff0c;什么是进程&#xff0c;有什么区别&#xff1f; 程序是静态的概念&#xff0c;当我们使用gcc xxx.c -o pro进行编译时&#xff0c;产生的pro文件&#xff0c;就是一个程序。 进程是程序的一次运行活动&#xff0c;通俗点就是说程序跑起来了就是进程。 …
阅读更多...
docker学习笔记（四）制作镜像

docker学习笔记（四）制作镜像

目录 第1步&#xff1a;编辑Dockerfile 第2步&#xff1a;编辑requirements.txt文件 第3步&#xff1a;编辑app.py文件&#xff0c;我们的程序文件 第4步&#xff1a;生成镜像文件 第5步&#xff1a;使用镜像&#xff0c;启动容器 第6步&#xff1a; 启动redis容器、将容器…
阅读更多...
PLC数据采集网关的功能和特点-天拓四方

PLC数据采集网关的功能和特点-天拓四方

一、引言 随着工业自动化程度的不断提高&#xff0c;数据在生产线上的作用愈发重要。PLC作为工业自动化的核心设备&#xff0c;其数据采集和处理能力直接影响到整个生产线的效率和稳定性。而PLC数据采集网关&#xff0c;作为连接PLC与外部系统的桥梁&#xff0c;正日益受到人们…
阅读更多...
我的Transformer专栏来啦

我的Transformer专栏来啦

五一节前吹的牛&#xff0c;五一期间没完成&#xff0c;今天忙里偷闲&#xff0c;给完成了。 那就是初步拟定了一个《Transformer最后一公里》的写作大纲。 之前一直想写一系列Transformer架构的算法解析文章&#xff0c;但因为一直在忙&#xff08;虽然不知道在忙啥&#xf…
阅读更多...
YOLOv8 Tensorrt Python/C++部署详解

YOLOv8 Tensorrt Python/C++部署详解

按照大佬的方法进行部署&#xff0c;但是中间出现了很多问题&#xff0c;这里进行一下总结。 YOLOv8 Tensorrt Python/C部署教程_yolo 安装tensorrt-CSDN博客https://blog.csdn.net/weixin_45747759/article/details/130341118 Monday-Leo/Yolov5_Tensorrt_Win10: A simple i…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023