树和二叉树的定义和基本术语

news2024/11/20 13:24:20

文章目录

前言
一、树的定义
二、树的基本术语
三、二叉树的定义
总结

前言

T_T此专栏用于记录数据结构及算法的（痛苦）学习历程，便于日后复习（这种事情不要啊）。所用教材为《数据结构 C语言版第2版》严蔚敏。

一、树的定义

树(Tree),是 n (n>=0)个结点的有限集，它或为空树(n = 0); 或为非空树，对于非空树T:
(1)有且仅有一个称之为根的结点；
(2)除根结点以外的其余结点可分为 m (m>0) 个互不相交的有限集 T1, T2…其中每一个集合本身又是一棵树，并且称为根的子树(SubTree)。
例如，在下图中，(a)是只有一个根结点的树；(b)是有13个结点的树，其中A是根结点，其余结点分成3个互不相交的子集： T1={B,E, F, K, L}, T2={C,G}, T3= {D, H, I, J, M}。Ti、T2和T3都是根A的子树，且本身也是一棵树。例如T1，其根结点为B, 其余结点分为两个互不相交的子集： T11= {E, K, L} , T12 = {F}。T11中 E 又是一个子树的根结点…
在这里插入图片描述
因此可知，树的结构定义是一种递归定义（链表？？？（幻视）），且数据关系是一对多。

二、树的基本术语

(1) 结点：树中的一个独立单元。包含一个数据元素及若干指向其子树的分支，如上图(b) 中的 A 、 B 、 C 、 D 等。
(2)结点的度（degree）：结点拥有的子树数量称为结点的度。例如，A的度为 3, C的度为 1, F的度为 0。
(3)树的度：树的度是树内各结点度的最大值。上图 (b) 所示的树的度3。
(4) 叶子：度为 0 的结点称为叶子或终端结点。结点 K 、 L 、 F 、 G 、 M 、 I 、 J都是树的叶子。
由此，树的根结点无前驱有后继（n>1），叶子有前驱无后继。注意这里的根节点仅指最大一棵树的根节点，如上图中的A结点,而B结点显然不是最大树的根节点。
(5) 非终端结点：度不为 0 的结点称为非终端结点或分支结点。除根结点之外，非终端结点也称为内部结点，如上图中的E、B、C、D和H。
(6)双亲和孩子：结点的子树的根称为该结点的孩子，相应地，该结点称为孩子的双亲。例如，B的双亲为A, B的孩子有E和F。即结点前驱为双亲，后继为孩子。
(7) 兄弟：同一个双亲的孩子之间互称兄弟。例如，H 、 I 和J互为兄弟。
(8) 祖先：从根结点到该结点所经分支上的所有结点。例如， M 的祖先为 A 、 D 和H。
(9) 子孙：以某结点为根的子树中的任一结点都称为该结点的子孙。如 B 的子孙为E 、 K 、 L和F。
(10) 层次(level)：结点的层次从根开始定义起，根为第一层，根的孩子为第二层。树中任一结点的层次等千其双亲结点的层次加1。
(11)堂兄弟：双亲在同一层的结点互为堂兄弟。例如，结点 G 与E 、 F、 H 、 I 、 J互为堂兄弟。
(12)树的深度(height)：树中结点的最大层次称为树的深度或高度。上图所示的树的深度为4。
(13)有序树和无序树：如果将树中结点的各子树看成从左至右是有次序的（即不能互换），则称该树为有序树，否则称为无序树。在有序树中最左边的子树的根称为第一个孩子，最右边的称为最后一个孩子。
(14)森林：是 m (m>=0)棵互不相交的树的集合。对树中每个结点而言，其子树的集合即为森林。由此，也可以用森林和树相互递归的定义来描述树。

三、二叉树的定义

任何树都可以转化为二叉树，而二叉树的许多操作算法简单，因此必须掌握二叉树。
首先明确一点：二叉树不是树！！！二叉树不是树！！！二叉树不是树！！！（原因见下）
二叉树(Binary Tree)是 n (n>=0)个结点所构成的集合，它或为空树(n = 0); 或为非空树，对于非空树T:
(1) 有且仅有一个称之为根的结点T；
(2)除根结点以外的其余结点分为两个互不相交的子集T1和T2, 分别称为T的左子树和右子树，且T1和T2本身又都是二叉树。
二叉树与树一样具有递归性质，二叉树与树的区别主要有以下两点：
(1)二叉树每个结点至多只有两棵子树（即二叉树中不存在度大于2 的结点）；
(2)二叉树的子树有左右之分，其次序不能任意颠倒。
&emsp二叉树的递归定义表明二叉树或为空，或是由一个根结点加上两棵分别称为左子树和右子树的、互不相交的二叉树组成。由于这两棵子树也是二叉树，由二叉树的定义，它们也可以是空树。由此，二叉树可以有5种基本形态，如下图所示。
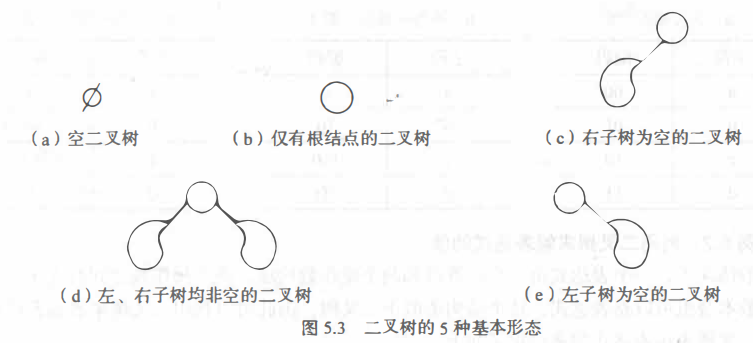
在这里插入图片描述
由此可知，对于一个根节点带一个子树的结构，即c和d，在二叉树中仍然是两个不同的结构，但在树中却是相同的结构，从而，二叉树不是树（强碱不是碱，是盐！）。但上述对树的基本属于在二叉树中也适用。