文章目录
- 一、说明
- 二、双曲几何的上半平面模型
- 三、距离问题
- 四、弧长微分
- 五、面积问题
- 六、python实现
一、说明
我们知道,双曲几何的著名模型有四种:微分解析模型、庞加莱盘、庞加莱半平面、克莱因盘。庞加莱圆盘模型是表示双曲几何的一种方法,对于大多数用途来说它都非常适合几何作图。然而,另一种模型,称为上半平面模型,使一些计算变得更容易,包括三角形面积的计算。
二、双曲几何的上半平面模型
双曲几何的上半平面模型具有空间 U 由所有复数组成 z 这样我( z) > 0 , 和转化组 U 包括发送的所有莫比乌斯变换 U 对自己。空间 U 称为上半平面 C。
双曲几何的庞加莱圆盘模型可以通过由两次反演构建的莫比乌斯变换转移到上半平面模型,如下所示:
- 围绕圆反转 C 以i为圆心,经过 - 1 和 1 如图 5.5.1 。
- 对实轴对称。
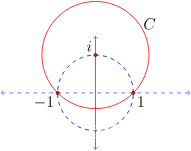
注意圆的反转C固定- 1和1,并且需要将i映射到无穷大。
由于穿过实轴的反射使这些图像点固定,因此两个反演的组合是莫比乌斯变换,它将单位圆带到实轴。该图还将圆盘的内部发送到上半平面。进一步注意莫比乌斯变换需要无穷大到-i;
因此,由定理3.5.1,map可以写成
V ( z ) = − i z + 1 z − i . . . . . . . . . . . . . . . . . . . . . . ( 5.5.1 ) V(z) = \dfrac{-iz + 1}{z - i}\text{.} ..................... (5.5.1) V(z)=z−i−iz+1......................(5.5.1)
这种莫比乌斯变换是将双曲平面的圆盘模型转移到上半平面模型的关键。事实上,当在这些模型之间来回切换时,本节采用以下约定是很方便的:让z表示其中的一个点d ,和w表示上半平面中的一个点U ,如图5.5.2。我们记录连接下面空间的转换。
在 (D,H) 之间移动 和(U,U)。莫比乌斯变换 V 映射D 给你, 及其逆
V
−
1
V^{-1}
V−1, 由下式给出:
w = V ( z ) = − i z + 1 z − i , 和 z = V 1 ( w ) = i w + 1 w + i . . . . . . . . ( 5.5.2 ) w=V(z)=\frac{−iz+1}{z−i }, 和 z=V_1(w)=\frac{iw+1}{w+i}........(5.5.2) w=V(z)=z−i−iz+1,和z=V1(w)=w+iiw+1........(5.5.2)
上半平面模型的一些特征立即显现出来。自从V是莫比乌斯变换,它保留斜线和角度。这意味着圆盘模型中的理想点,即无穷远圆上的点,
S
1
S_1
S1无穷大,
已移动到实轴,并且圆盘模型中的双曲线已变为与实轴成直角相交的斜线。
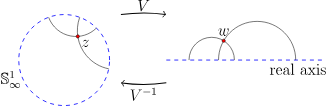
图-5.5. 2:将圆盘映射到上半平面。
三、距离问题
定义两点之间的双曲距离w1,w2在上半平面模型中,表示为 d U ( w 1 , w 2 ) d_U(w1,w2) dU(w1,w2),是圆盘模型中它们的原像之间的双曲距离。
认为w1和w2有两点在V其单位圆盘中的原像为z1和z2,分别。然后,
d
U
(
w
1
,
w
2
)
=
d
H
(
z
1
,
z
2
)
=
l
n
(
(
z
1
,
z
2
;
u
,
v
)
)
.
.
.
.
.
.
.
.
.
.
(
5.5.3
)
d_U(w1,w2)=d_H(z1,z2)=ln((z1,z2;u,v)).......... (5.5.3)
dU(w1,w2)=dH(z1,z2)=ln((z1,z2;u,v))..........(5.5.3)
在这里u和v是双曲线的理想点z1和z2。但是,由于交叉比在莫比乌斯变换下得以保留,
d
U
(
w
1
,
w
2
)
=
l
n
(
(
w
1
,
w
2
;
p
,
q
)
)
.
.
.
.
.
.
.
.
.
.
.
.
(
5.5.4
)
d_U(w1,w2) = ln((w1,w2; p,q))............(5.5.4)
dU(w1,w2)=ln((w1,w2;p,q))............(5.5.4)
在这里,是上半平面中双曲线的理想点w1和w2。特别是,从w1到w2我们正在走向理想点p 。
例子5.5. 1: 虚轴上点之间的距离ri和si。因为r > s > 0我们计算之间的距离我和我在上半平面模型中。
双曲线通过ri和si是正虚轴,有理想点0和无穷大。因此,
d
U
(
r
i
,
s
i
)
=
ln
(
(
r
i
,
s
i
;
0
,
∞
)
)
=
r
i
−
0
r
i
−
∞
⋅
s
i
−
∞
s
i
−
0
=
ln
(
r
s
)
.
\begin{align*} d_U(ri, si) & = \ln((ri, si; 0, \infty))\\ & = \dfrac{ri - 0}{ri - \infty}\cdot\dfrac{si-\infty}{si-0}\\ & = \ln\left(\dfrac{r}{s}\right)\text{.} \end{align*}
dU(ri,si)=ln((ri,si;0,∞))=ri−∞ri−0⋅si−0si−∞=ln(sr).
例子5.5.2 :任意两点之间的距离。
求任意两点之间的距离 w1 和w2 在
U
\mathbb{U}
U 中, 我们首先在上半平面模型中构建一个映射,将这两个点移动到正虚轴。为了构建这张图,我们使用庞加莱圆盘模型。
通过改造
V
1
V_1
V1我们发送w1和w2回到
D
\mathbb{D}
D .我们让
z
1
=
V
1
(
w
1
)
z_1=V_1(w1)
z1=V1(w1)
和
z
2
=
V
1
(
w
2
)
z_2=V_1(w_2)
z2=V1(w2)。然后,让
S
(
z
)
=
e
i
θ
z
−
z
1
1
−
z
1
ˉ
z
S(z)=e^{iθ}\frac{z−z1}{1−\bar{z_1}z}
S(z)=eiθ1−z1ˉzz−z1
是转变
(
D
、
H
)
(\mathbb{D}、\mathcal{H})
(D、H)发送z1到0和θ仔细选择,以便
z
2
z_2
z2被发送到正虚轴。实际上,z2被发送到ki,在这里
k
=
∣
S
(
z
2
)
∣
=
∣
S
(
V
−
1
(
w
2
)
)
∣
k = | S(z_2) | = | S(V^{- 1}(w_2) ) |
k=∣S(z2)∣=∣S(V−1(w2))∣(和0 < k < 1)。然后,申请V就情况而言,0被发送到i,和ki被发送到
1
+
k
1
−
k
i
\frac{1 + k}{1 − k}i
1−k1+ki我。因此,
V
∘
S
∘
V
−
1
V∘ S∘V^{- 1}
V∘S∘V−1发送w1到i;和w2
到
1
+
k
1
−
k
i
\frac{1 + k}{1 − k}i
1−k1+ki,其中通过前面的示例,点之间的距离是已知的:
d
U
(
w
1
,
w
2
)
=
l
n
(
1
+
k
)
−
l
n
(
1
−
k
)
.
.
.
.
.
.
.
.
.
.
.
.
.
(
5.5.5
)
dU(w1,w2) = ln( 1 + k ) − ln( 1 − k ) .............(5.5.5)
dU(w1,w2)=ln(1+k)−ln(1−k).............(5.5.5)
描述k按照w1和w2留给有冒险精神的读者。我们不需要在这里追究这个问题。
四、弧长微分
现在,我们再次通过圆盘模型导出上半平面模型的双曲弧长微分。回想一下圆盘模型中的弧长微分是
d
s
=
2
∣
d
z
∣
1
−
∣
z
∣
2
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
(
5.5.6
)
ds = \dfrac{2|dz|}{1-|z|^2}\text{.}..............................(5.5.6)
ds=1−∣z∣22∣dz∣...............................(5.5.6)
自从
z
=
V
−
1
(
w
)
=
i
w
+
1
w
+
i
z = V^{-1}(w) = \dfrac{iw+1}{w+i}
z=V−1(w)=w+iiw+1 我们可以计算出弧长微分dw。
我们需要对复杂表达式求导,这可以像实值表达式一样进行。开始了:
d s = 2 ∣ d z ∣ 1 − ∣ z ∣ 2 = 2 ∣ d ( i w + 1 w + i ) ∣ 1 − ∣ i w + 1 w + i ∣ 2 = 2 ∣ i ( w + i ) d w − ( i w + 1 ) d w ∣ ∣ w + i ∣ 2 / [ 1 − ∣ i w + 1 ∣ 2 ∣ w + i ∣ 2 ] = 4 ∣ d w ∣ ∣ w + i ∣ 2 − ∣ i w + 1 ∣ 2 = 4 ∣ d w ∣ ( w + i ) ( w ‾ − i ) − ( i w + 1 ) ( − i w ‾ + 1 ) = 4 ∣ d w ∣ 2 i ( w ‾ − w ) = ∣ d w ∣ I m ( w ) . \begin{align*} ds & = \dfrac{2|dz|}{1-|z|^2}\\ & =\dfrac{2|d\bigg(\dfrac{iw+1}{w+i}\bigg)|}{1-\bigg|\dfrac{iw+1}{w+i} \bigg|^2} \tag{$z = \dfrac{iw+1}{w+i}$}\\ & =\dfrac{2|i(w+i)dw-(iw+1)dw|}{|w+i|^2}\bigg/\bigg[1-\dfrac{|iw+1|^2}{|w+i|^2}\bigg]\tag{chain rule}\\ & = \dfrac{4|dw|}{|w+i|^2-|iw+1|^2}\\ & = \dfrac{4|dw|}{(w+i)(\overline{w}-i)-(iw+1)(-i\overline{w}+1)}\\ & = \dfrac{4|dw|}{2i(\overline{w}-w)}\\ & = \dfrac{|dw|}{{ Im}(w)}\text{.} \end{align*} ds=1−∣z∣22∣dz∣=1− w+iiw+1 22∣d(w+iiw+1)∣=∣w+i∣22∣i(w+i)dw−(iw+1)dw∣/[1−∣w+i∣2∣iw+1∣2]=∣w+i∣2−∣iw+1∣24∣dw∣=(w+i)(w−i)−(iw+1)(−iw+1)4∣dw∣=2i(w−w)4∣dw∣=Im(w)∣dw∣.(z=w+iiw+1)(chain rule)
这使我们得出以下定义:
定义:平滑曲线的长度平滑曲线的长度 r ( t ) r ( t ) r(t)为了 a ≤ t ≤ b a≤t≤b a≤t≤b在上半平面模型中 ( U , U ) , (\mathbb{U},{\cal U})\text{,} (U,U),表示 L ( r ) , {\cal L}(\boldsymbol{r})\text{,} L(r), 给出弧长的积分
L ( r ) = ∫ a b ∣ r ′ ( t ) ∣ Im ( r ( t ) ) d t . . . . . . . . . ( 5.5.7 ) {\cal L}(\boldsymbol{r}) = \int_a^b \dfrac{|\boldsymbol{r}^\prime(t)|}{\text{Im}(\boldsymbol{r}(t))}~dt\text{.}........(5.5.7) L(r)=∫abIm(r(t))∣r′(t)∣ dt.........(5.5.7)
例子5.5.3:曲线的长度。
求水平曲线的长度
r
(
t
)
=
t
+
k
i
r ( t ) = t + k i
r(t)=t+ki设定了
a
≤
t
≤
b
a≤t≤b
a≤t≤b ,注意
r
′
(
t
)
=
1
r^′( t ) = 1
r′(t)=1
和
I
m
(
r
(
t
)
)
=
k
Im ( r ( t ) ) = k
Im(r(t))=k 。因此,
L
(
r
)
=
∫
a
b
1
k
d
t
=
b
−
a
k
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
(
5.5.8
)
{\cal L}(\boldsymbol{r}) = \int_a^b \dfrac{1}{k}~dt = \dfrac{b-a}{k}\text{.}..................(5.5.8)
L(r)=∫abk1 dt=kb−a...................(5.5.8)
五、面积问题
由弧长微分 d s = d w Im ( w ) ds = \dfrac{dw}{\text{Im}(w)} ds=Im(w)dw 面积微分来了:
定义:区域面积
上半平面模型中 ( U , H ) (\mathbb{U} ,\mathcal{H}) (U,H)双曲几何中,一个区域的面积R 用笛卡尔坐标描述,表示为一个 A ( R ) A(R ) A(R),给出积分实现:
A ( R ) = ∬ R 1 1 y 2 d x d y . . . . . . . . . . . . . . . . . . . . . . . . . . . . ( 5.5.9 ) A (R )=∬_ {R_1}\frac{1}{y^2} dxdy ............................(5.5.9) A(R)=∬R1y21dxdy............................(5.5.9)
例子5.5.4:求一个2/3-理想的三角形 的面积。
认为 w ∈ U w ∈ U w∈U位于单位圆上,并考虑2/3-理想三角形的区域1w∞,就是下图蓝线包围的区域,如图所示。
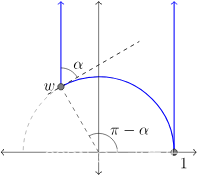
特别地,假设内角为w是α ,以便
w
=
e
i
(
π
−
α
)
w =e^{i( π- α )}
w=ei(π−α)在里这0 < α < π。
这个面积2/3- 理想三角形是这样的面积:
A
=
∫
cos
(
π
−
α
)
1
∫
1
−
x
2
∞
1
y
2
d
y
d
x
=
∫
cos
(
π
−
α
)
1
1
1
−
x
2
d
x
.
\begin{align*} A & = \int_{\cos(\pi - \alpha)}^1 \int_{\sqrt{1-x^2}}^\infty \dfrac{1}{y^2}~dydx\\ & = \int_{\cos(\pi - \alpha)}^1 \dfrac{1}{\sqrt{1-x^2}}~dx\text{.} \end{align*}
A=∫cos(π−α)1∫1−x2∞y21 dydx=∫cos(π−α)11−x21 dx.
用三角函数替换
cos
(
θ
)
=
x
,
\cos(\theta) = x\text{,}
cos(θ)=x,,以便,
1
−
x
2
=
sin
(
θ
)
\sqrt{1-x^2} = \sin(\theta)
1−x2=sin(θ)因此有:
−
sin
(
θ
)
d
θ
=
d
x
,
-\sin(\theta)d\theta = dx\text{,}
−sin(θ)dθ=dx,
积分变为:
=
∫
π
−
α
0
−
sin
(
θ
)
sin
(
θ
)
d
θ
=
π
−
α
.
\begin{align*} & =\int_{\pi - \alpha}^0\dfrac{-\sin(\theta)}{\sin(\theta)}~d\theta\\ & = \pi - \alpha\text{.} \end{align*}
=∫π−α0sin(θ)−sin(θ) dθ=π−α.
事实证明,任何2/3- 理想三角形与其中一种形式全等1w∞,在这里w,位于单位圆的上半部分,并且由于我们的变换保留了角度和面积,因此我们已经证明了面积公式2/3-理想三角形。
定理5.5.1的面积为2/3-具有内角的理想三角形α,面积等于π- α 。
六、python实现
以下给出潘家来半平面的实验代码,其执行效果是:
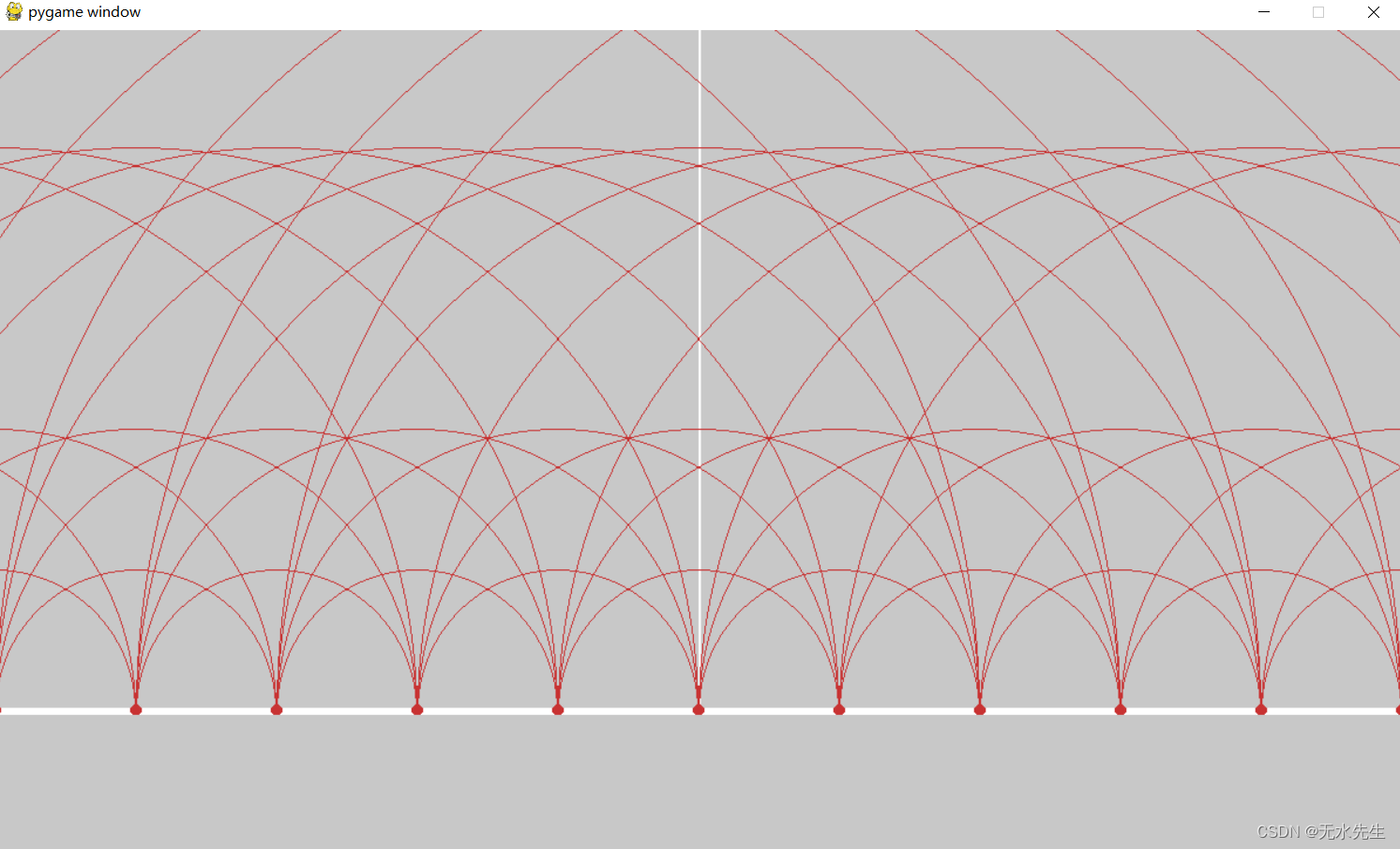
所有的依赖库:
import pygame
import math
import numpy as np
import scipy
from scipy.linalg import fractional_matrix_power
外加两个自开发库:
from PoincarePlot import PoincarePlot
from Line import Line
因为代码数量较大,请需要的读者自行下载。