基本模型及解释
分位数回归经典模型是由Koenker和Bassett (1978b)引入的,它从位置模型中的普通分位数(也称为“百分位数”)的概念扩展到更一般的一类线性模型,其中条件分位数具有线性形式。为了简单地回忆一下普通分位数,考虑一个实数随机变量Y,其特征如下分布函数

则对于任意τ∈(0,1),Y的τ -th分位数定义如下:
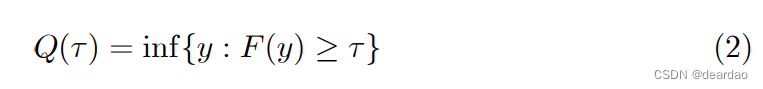
中位数是Q(1/2),第一个四分位数是Q(1/4),第一个十分位数是Q(1/10)。分位数函数提供了Y的完整表征,就像分布函数f一样。分位数可以写成以下优化问题的解:对于任意τ∈(0,1),定义分段线性的“检验函数”
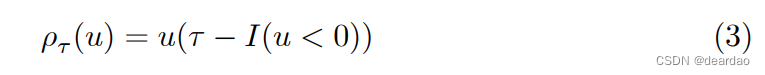
其中I(.)是常用的指示函数。最小化问题的解是
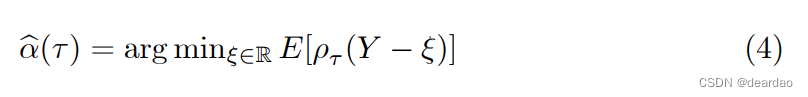
Q(τ)的样本模拟是基于一个随机样本{y1,…, n} (Y)。然后,根据上述(4)的精神,可以将τ -th分位数识别为以下问题的任何解: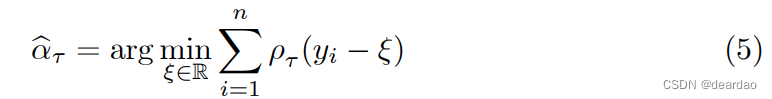
设xi = 1…n,一个K × 1的回归量向量。然后,我们可以将表达式(1)的等价物写成:
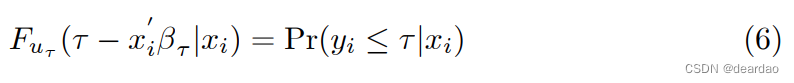
它本质上是一种不同的形式,来自于更熟悉的:

其中误差项uτ i的分布未指定,唯一的约束是(通常的)分位数限制Qτ (uτ i |xi)=0。
用条件平均函数的估计作为类比,如
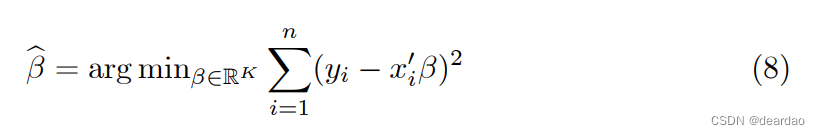
线性条件分位数函数
通过对这种情况求解式(8)的等价可以估计: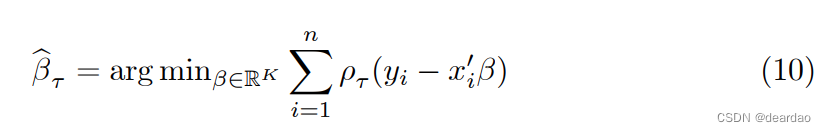
我们还没有问分位数回归的解释问题。平均回归模型的最小二乘估计器将关注Y的条件均值对协变量X的依赖性。分位数回归估计器在条件分布的每个分位数上解决这个问题,从而提供了一个更完整的描述,即给定X = x的Y的条件分布如何依赖于X。换句话说,而不是假设协变量仅改变条件分布的位置或规模,分位数回归也考察了对分布形状的潜在影响。
让我们再看一个更实际的问题:人们对分位数的系数有什么解释?例如所述Buchinsky (1998), y的条件分位数的偏导数(见上面(9))对解释变量之一,说j的,是被解读为τ的边际变化th分位数由于边际变化j元素x,如果进一步的假设在这一节中,x 有K个不同的变量,那么这个导数只是j变量的系数,βj。然而,在解释这一结果时需要谨慎:这当然并不意味着碰巧处于一个条件分布的第τ -th分位数的受试者,如果他/她的x的相应值发生变化,他/她仍然会发现自己在那里。
在本报告的介绍中,我提到了相对于均值回归估计的情况下,分位数回归的稳健性。由于分布假设的稳健性通常是整个统计中的一个关键考虑因素,因此有必要在分位数回归的上下文中多说几句。关于鲁棒性解释确实有一个非常好的消息,因为估计和推理过程具有固有的无分布特性,因为分位数估计只受指定分位数附近响应的条件分布的局部行为的影响。残差的符号是确定估计时唯一重要的东西,因此响应变量值中的异常值影响拟合,只要它们高于或低于拟合的超平面,但低于或高于多远实际上是无关紧要的。然而,并非所有事情都是如此积极:虽然我们刚刚看到分位数回归估计对响应观测值的污染具有固有的鲁棒性,但它们对设计观测值的污染可能相当敏感。