一篇文章彻底搞懂折半查找法[二分查找法]算法~

news2024/10/5 14:18:07

算法实现的要求：

折半查找法又称为二分查找法，这种方法对待查找的列表有两个要求：

1：必须采用顺序存储结构
2：必须按关键字大小有序排列

算法思想：

将表中间位置记录的关键字与查找关键字进行比较，如果两者相等，则查找成功，否则利用中间位置记录将表分成前后两个子表，如果中间位置记录的关键字大于查找关键字，则进一步查找前一子表，否则进一步查找后一子表

重复上述查找过程，直到找到满足条件的记录，则查找成功，或直到子表不存在为止，则查找不成功

使用java实现该算法：

算法实现方法：

1：前提要求：有已排序数组A，[因为在查找的过程中是根据下标进行的]

2：定义左边界L，右边R，确定搜索范围，循环执行二分查找

3：获取中间索引M=(L+R)/2，如果是小数，一般默认向下取整

4：中间索引的值A[M]与带搜索的值T进行比较
A[M]==T，返回中间索引
A[M]>T,中间值右侧的其他元素都大于T,无需比较，中间索引左边去找，M-1,设置为右边界，重新查找
A[M]<T,中间值左侧的其他元素都小于T,无需比较，中间索引右边去找，M+1设置为左边界，重新查找

5：当L>R时，表示没有找到，应结束循环

代码如下所示：

package bin_find;

import java.util.Scanner;

public class bin_find {
    public static void main(String[] args) {
        int arr[] = {4, 10, 18, 23, 45, 68, 199};
        Scanner scanner = new Scanner(System.in);
        System.out.println("请输入你要查找的数：");
        int x = scanner.nextInt();
        int result= bin_research(arr,x);
        if(result!=-1){
            System.out.println("你要查找的数已找到，它是数组的第"+(result+1)+"个元素");
        }
        else{
            System.out.println("你要查找的数不存在");
        }
    }

    public static int bin_research(int arr[], int x) {
        int L = 0;
        int R = arr.length - 1;
        while(L<=R) {
        //不要写到循环外面了，因为每查找一次，中间索引的位置也需要变化
            int M = (L + R) / 2;
            if (x > arr[M]) {
                L = M+1;
            } else if (x < arr[M]) {
                R = M - 1;
            } else if (x == arr[M]) {
                return M;
            }
        }
        return -1;
    }
}

输出：

请输入你要查找的数：
23
你要查找的数已找到，它是数组的第4个元素

整数溢出现象：

package bin_find;

public class bin_find2 {
    public static void main(String[] args) {
        int l=0;
        int r=Integer.MAX_VALUE-1;
        int m=(l+r)/2;
        //当要查找的数在左子表时：
        System.out.println(m);
        //当要查找的数在右子表时：发生整数溢出现象
        l=m+1;
        m=(l+r)/2;
        System.out.println(m);
    }
}

输出：

1073741823
-536870913

之所以会出现负数的原因：是因为在计算机中，是根据二进制进行运算的，逢二进一，由于最高位表示符号位，当它为1时，该数即为负数！

对该过程不熟悉的小伙伴，可以去看我写的这篇文章

解决整数溢出问题：

上述代码中产生溢出的原因是由于：当要查找的数在右子表时，此时：r最初为整数的最大值-1不变，而l的值增大到了r/2的大小，因此即使他两相加除2，在计算机中，是根据二进制进行运算的，逢二进一，由于最高位表示符号位，当它为1时，该数即为负数，那么解决溢出的核心就是改变m的值，但所谓的改变，并不是将m的值真正的改变，而是通过变换表达式等等，去调整m的大小

方法1：通过调整数学表达式

方法如下：

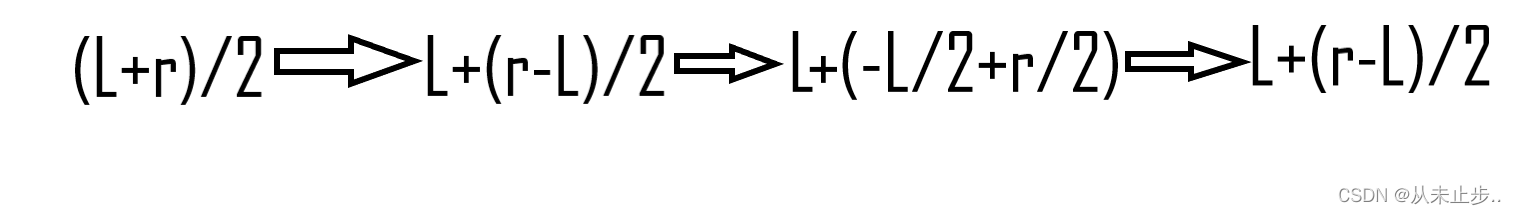
在这里插入图片描述

代码如下：

package bin_find;

public class bin_find2 {
    public static void main(String[] args) {
        int l=0;
        int r=Integer.MAX_VALUE-1;
        int m=l+(r-l)/2;
        //当要查找的数在左子表时：
        System.out.println(m);
        //当要查找的数在右子表时：
        l=m+1;
        m=l+(r-l)/2;
        System.out.println(m);
    }
}

输出：

1073741823
1610612735

方法2：通过>>>运算符

>>>表示无符号右移运算符，也叫逻辑右移，即若该数为正，则高位补0，而若该数为负数，则右移后高位同样补0，移动的是二进制位，但他们的操作数必须是整数，[当被操作的数是整数时]右移一位有除二的效果，因此对于上述溢出现象，右移一位既能够避免最高位[符号位]为1，导致该数为负数的现象，而且正好借用它右移一位有除二的效果，还简化了数学表达式；

修改如下：

package bin_find;

public class bin_find2 {
    public static void main(String[] args) {
        int l=0;
        int r=Integer.MAX_VALUE-1;
        int m=(r+l)>>>1;
        //当要查找的数在左子表时：
        System.out.println(m);
        //当要查找的数在右子表时：
        l=m+1;
        m=l+(r-l)>>>1;
        System.out.println(m);
    }
}