文章目录
- 模型部署教程来啦:)
- 什么是Roofline Model?
- 算法模型相关指标
- 计算量
- 计算峰值
- 参数量
- 访存量
- 带宽
- 计算密度
- kernel size对计算密度的影响
- output size对计算密度的影响
- channel size对计算密度的影响
- group convolution对计算密度的影响
- tensor reshape对计算密度的影响
- 全连接层对计算密度的影响
- 对单个模型构建Roofline Model
- Nsight Compute⼯具⾃动搭建roofline Model
- 总结
- 参考
模型部署教程来啦:)
模型部署白皮书❤️🔥❤️🔥❤️🔥
什么是Roofline Model?
想象一下,如果我们想让一辆车跑得更快,我们需要知道它现在能跑多快,是什么在限制它的速度(比如是引擎的问题,还是轮胎的摩擦),以及我们可以做哪些改动来让它跑得更快。在计算机和程序的世界里,我们也有类似的方法来帮助我们理解和提升一个程序的运行速度,这就是所谓的“Roofline Model”(屋顶模型)。
屋顶模型就像是一个图表,帮助我们看到一个程序在特定的计算机上能跑得多快,以及是什么在限制它跑得更快。这个模型被画成一张图,上面有两条线:
-
屋顶线(Roofline):这条线像房子的屋顶一样,代表了最快的速度,即计算机的最大性能。你可以把它想象成车能达到的最高速度。这个速度有两部分限制:一部分是计算机处理数据的速度(比如引擎有多强),另一部分是计算机从内存中获取数据的速度(比如路上的限速标志)。
-
程序的点:图表上的每一个点代表了一个程序或者程序的一部分。这个点的位置会告诉我们程序现在的速度有多快,以及是什么在限制它——是处理数据的速度,还是获取数据的速度。

其实 Roof-line Model 说的是很简单的一件事:模型在一个计算平台的限制下,到底能达到多快的浮点计算速度。更具体的来说,Roof-line Model 解决的,是“计算量为A且访存量为B的模型在算力为C且带宽为D的计算平台所能达到的理论性能上限E是多少”这个问题。接下来让我们了解一些和Roofline Model相关的基本概念。
算法模型相关指标
计算量
-
定义:针对单个输入,模型完成一次完整的向前传播所发生的浮点运算个数(FLOPs,
floating point operations),也即模型的时间复杂度。 -
计算⽅式: M 2 ∗ K 2 ∗ C i n ∗ C o u t M^2*K^2*C_{in}*C_{out} M2∗K2∗Cin∗Cout
M: 卷积核输出特征图的H和W。不同的时候可以用Mh, Mw表示 K: 卷积核大小
(严格来说应该乘以2,不然实际上算的是MACs值。MACs、MAdds、FLOPs的区别:FLOPs=2*MACs=2*MAdds,乘累加操作MACs(Multiply‒Accumulate Operations)中 1MACs包含⼀个乘法操作与⼀个加法操作,所以MAdds通常是FLOPs值的⼆分之⼀。但在计算机视觉论⽂中,常常将⼀个乘加组合视为⼀次浮点运算,所以也会常⻅到将MACs值作为Flops的,⽽且常⻅的计算⼯具都是按照不乘以2计算的)
计算峰值
单位是FLOPS (也可以是FLOP/s), 表示计算机每秒可以执行的 floating point operations。是衡 量计算机性能的标准
参数量
单位是Byte,表示模型中所有 的weights(主要在conv和FC中) 的量。是衡量模型大小的标准。
访存量
针对单个输入,模型完成一次完整的向前传播所发生的内存交换总量(read/write),**也即模型的空间复杂度。**单位:Byte
计算方式:*(每层输入的特征图内存占用+模型参数内存占用+每层输出的特征图内存占用)4,由于模型训练时数据类型一般是float32,所以换算成Byte需要乘以4
M A C s C o n v = M A C s I n p u t + M A C s W c i g h t + M A C s O u t p u t = ( N × I C × I H × I W + O C × I C × K H × K W + N × O C × O H × O W ) × s i z e o f ( d a t a _ t y p e ) \begin{aligned} MACs_{Conv}& =MACs_{Input}+MACs_{Wcight}+MACs_{Output} \\ &=(N\times IC\times IH\times IW+OC\times IC\times KH\times KW+N\times OC\times OH\times OW) \\ &\times sizeof(data\_type) \end{aligned} MACsConv=MACsInput+MACsWcight+MACsOutput=(N×IC×IH×IW+OC×IC×KH×KW+N×OC×OH×OW)×sizeof(data_type)
带宽
单位是Byte/s,全称是memory bandwidth, 表示的是单位时间内可以传输的数据量的多少。是衡量计算机硬件memory性能的一 个标准
带宽跟以下因素有关:
- memory clock (GHz) :表示的是单位时间内可以read/write的 频率(Hz),一般以GHz为基本单位
- memory bus width (Byte):如同字面意思,表示的是可以同时读写 的数据多少。单位是Byte
- memory channel:表示的是通道数量,越多越好
举几个例子:
NVIDIA Tesla V100
memory: HBM2
memory clock: 877 MHz
memory interface width: 512 Bytes (4096 bits)
=> memory bindwidth = 877 MHz * 512 Bytes * 2 = 898GB/s
NVIDIA Quadro RTX 6000
- memory: GDDR6 • memory clock: 1750 MHz
- memory clock effective: 1750 MHz * 8 = 14Gbps
- memory interface width: 48 Bytes (384 bits)
- => memory bindwidth = 14 Gbps * 48 Bytes * 1 = 672GB/s
怎么提高程序的带宽?
- 硬件层面:
使用更快的存储设备:使用固态硬盘(SSD)而不是传统机械硬盘(HDD)可以显著提高数据读写速度。
增强计算能力:通过使用更快的处理器或增加处理器核心数量来提升处理能力。在多核心系统上,可以并行处理数据以提高效率。
-
软件层面:
-
代码优化:通过剖析(Profiling)工具找出程序中的瓶颈,然后针对这些瓶颈进行优化。优化可能包括减少不必要的计算、使用更高效的算法或数据结构等。
-
并行计算:利用现代处理器的多核心特性,将任务分解成可以并行执行的子任务。对于大规模数据处理,可以考虑使用GPU进行并行计算。
-
减少数据传输量:如果带宽受限于数据传输,考虑使用数据压缩技术减少传输的数据量。对于网络应用,还可以通过优化通信协议来减少开销。
计算密度
计算密度(Computational intensity, I I I) I = n u m o f F L O P s / b y t e s o f d a t a ( F L O P s / B y t e ) I={numofFLOPs}/{bytesofdata}(FLOPs/Byte) I=numofFLOPs/bytesofdata(FLOPs/Byte),表示每Byte内存交换到底用于多少次浮点运算,计算强度越大,内存使用效率越高。
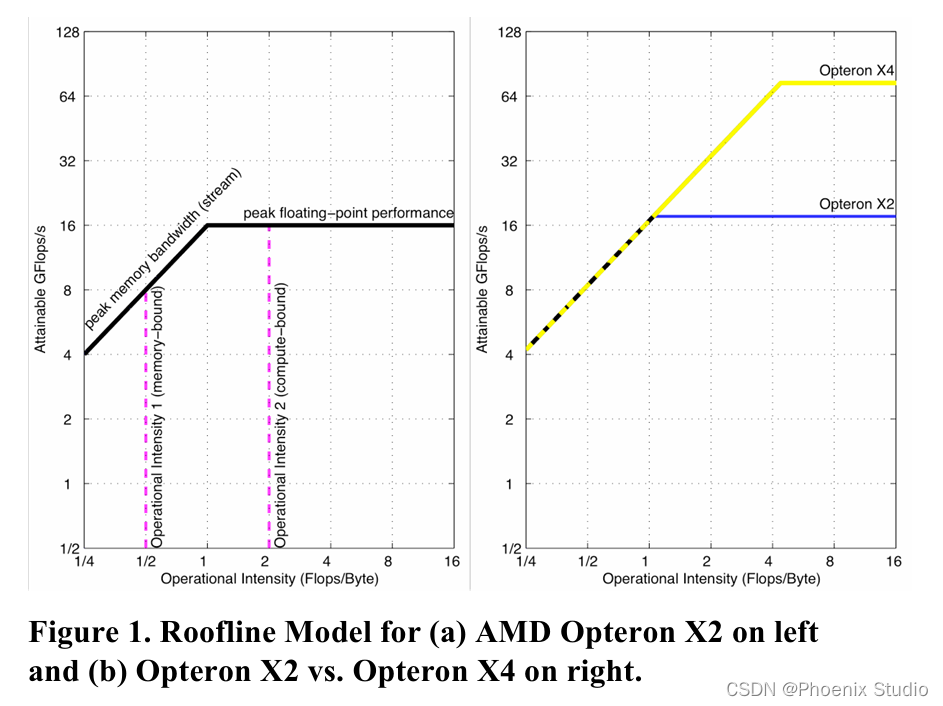
设Imax为拐点所对应的强度,是计算平台的计算强度上限。**当I<Imax时,模型的计算性能受限于宽带⼤⼩,处于宽带瓶颈区;当I>Imax时,模型的计算性能瓶颈取决于平台的算⼒,处于计算瓶颈区。**所以,模型的计算强度应尽量⼤于Imax,这样才能最⼤程度利⽤计算平台的算⼒资源,但超过之后就⽆需再追求⽆意义的提升,因为再强性能都只能达到计算平台的算⼒。
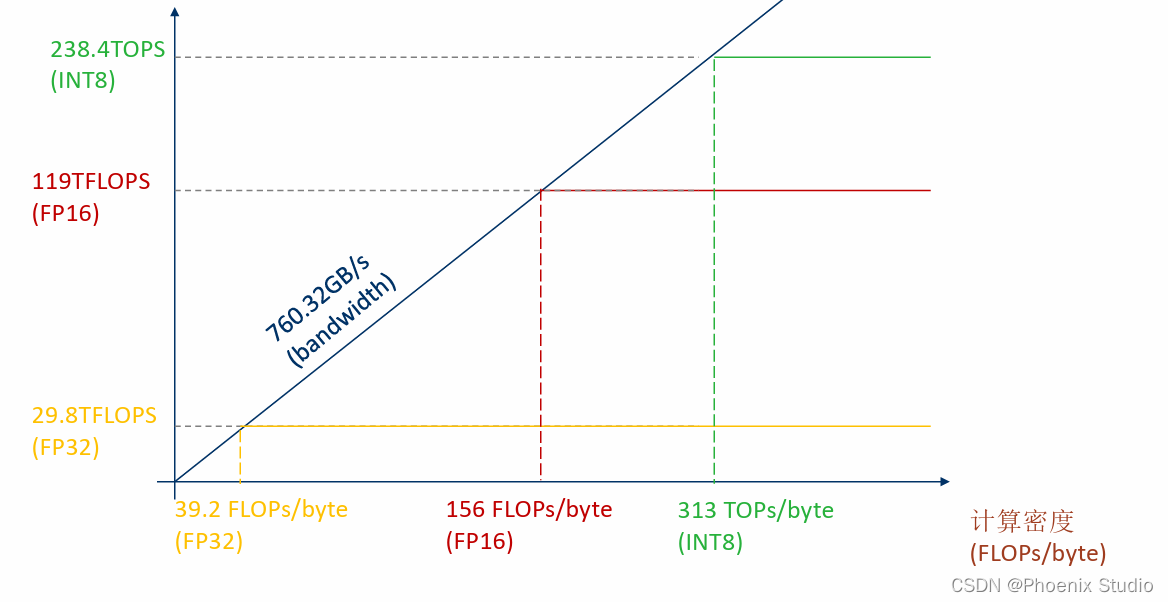
以3080 Ampere架构为例计算硬件的roofline model,相关参数如下:
- Core种类与数量
- 8704 CUDA cores
- 272 Tensor cores
- 68 SMs
- 计算峰值
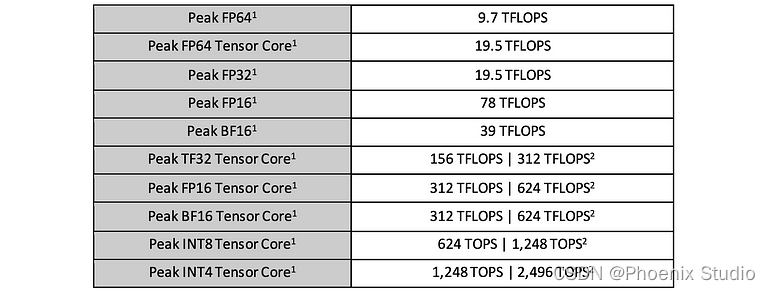
- (FP32) 29.8 TFLOPS
- (FP16) 119 TFLOPS
- (INT8) 238 TOPS
- 带宽
- 760.32 GB/s
- 频率
- 1.7GHz
FP32计算密度
- 计算峰值: 29.8 T F L O P S = 29.8 × 1 0 1 2 F L O P S 29.8 TFLOPS = 29.8 × 10^12 FLOPS 29.8TFLOPS=29.8×1012FLOPS
- 内存带宽: 760.32 G B / s = 760.32 × 1 0 9 b y t e s / s 760.32 GB/s = 760.32 × 10^9 bytes/s 760.32GB/s=760.32×109bytes/s
[ 计算密度 FP32 = 29.8 × 1 0 12 760.32 × 1 0 9 FLOPS/byte ] [ \text{计算密度}_{\text{FP32}} = \frac{29.8 \times 10^{12}}{760.32 \times 10^{9}} \, \text{FLOPS/byte} ] [计算密度FP32=760.32×10929.8×1012FLOPS/byte]
FP16计算密度
- 计算峰值: 119 T F L O P S = 119 × 1 0 1 2 F L O P S 119 TFLOPS = 119 × 10^12 FLOPS 119TFLOPS=119×1012FLOPS
- 内存带宽: 760.32 G B / s = 760.32 × 1 0 9 b y t e s / s 760.32 GB/s = 760.32 × 10^9 bytes/s 760.32GB/s=760.32×109bytes/s
[ 计算密度 FP16 = 119 × 1 0 12 760.32 × 1 0 9 FLOPS/byte ] [ \text{计算密度}_{\text{FP16}} = \frac{119 \times 10^{12}}{760.32 \times 10^{9}} \, \text{FLOPS/byte} ] [计算密度FP16=760.32×109119×1012FLOPS/byte]
INT8计算密度
- 计算峰值: 238 T O P S = 238 × 1 0 1 2 O P S 238 TOPS = 238 × 10^12 OPS 238TOPS=238×1012OPS
- 内存带宽: 760.32 G B / s = 760.32 × 1 0 9 b y t e s / s 760.32 GB/s = 760.32 × 10^9 bytes/s 760.32GB/s=760.32×109bytes/s
[ 计算密度 INT8 = 238 × 1 0 12 760.32 × 1 0 9 OPS/byte ] [ \text{计算密度}_{\text{INT8}} = \frac{238 \times 10^{12}}{760.32 \times 10^{9}} \, \text{OPS/byte} ] [计算密度INT8=760.32×109238×1012OPS/byte]
RTX 3080的计算密度如下:
- FP32: 约39.19 FLOPS/byte
- FP16: 约156.51 FLOPS/byte
- INT8: 约313.03 OPS/byte
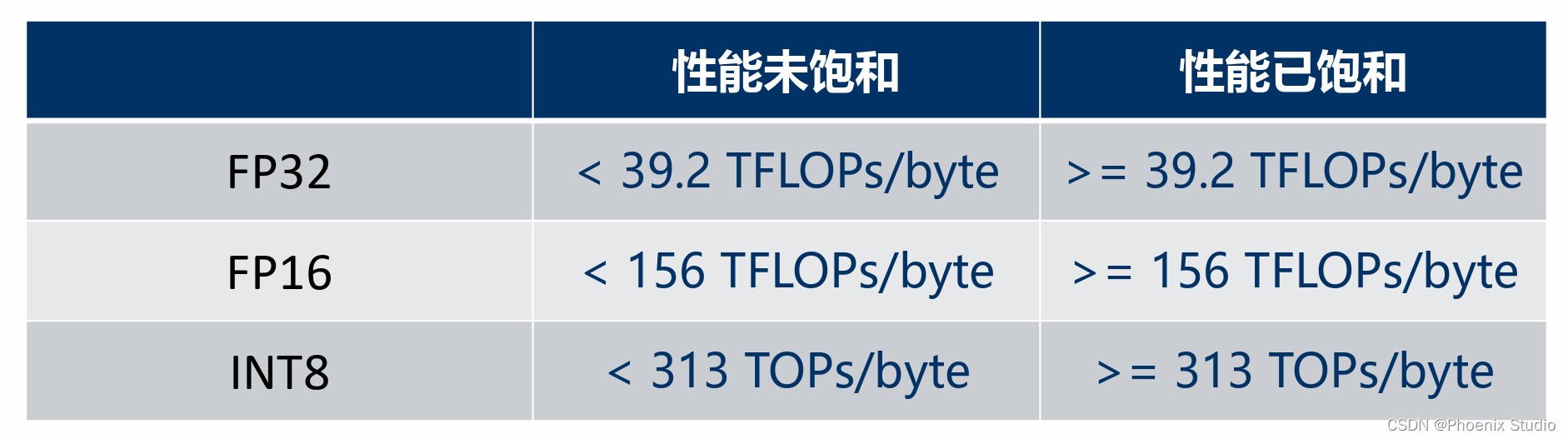
INT8运算的计算密度最高,意味着在处理INT8数据类型时,相对于内存带宽的限制,GPU能进行更多的计算,这在深度学习推理等场景中非常有用。
TOPS(Tera Operations Per Second)
- TOPS 主要用于衡量整数(包括定点)操作的性能。
- 它表示每秒可以执行的万亿次(Tera)操作,通常用于评估AI芯片、DSP(数字信号处理器)或其他专用硬件的性能,特别是在执行非浮点计算任务时。
TFLOPS(Tera Floating Point Operations Per Second)
- TFLOPS 专注于浮点数运算的性能。
- 它表示每秒可以执行的万亿次浮点运算,是评价GPU和CPU等计算设备在执行科学计算、图形处理和深度学习等浮点密集型任务性能的关键指标。
注意:Roofline Model是根据理论值计算得到的结果,实际使用的时候需要根据一系列benchmark找到部署架构的真实值。(比如自己写几个计算密集的核函数).因为实际计算过程中还有除算力和带宽之外的其他重要因素,它们也会影响模型的实际性能,这是 Roofline Model 未考虑到的。例如矩阵乘法,会因为 cache 大小的限制、GEMM 实现的优劣等其他限制,导致你几乎无法达到 Roofline 模型所定义的边界(屋顶)。
kernel size对计算密度的影响
定义模型如下:
class CustomConvNet(nn.Module):
def __init__(self):
super(CustomConvNet, self).__init__()
# 定义六层卷积层,卷积核大小分别为1, 3, 5, 7, 9, 11
# 计算padding,使得输出特征图大小保持为56x56,这里假设stride=1
# 对于任意卷积核大小k,padding可以设置为(k-1)/2(当k为奇数时)
self.conv1 = nn.Conv2d(256, 256, kernel_size=1, stride=1, padding=0)
self.conv2 = nn.Conv2d(256, 256, kernel_size=3, stride=1, padding=1)
self.conv3 = nn.Conv2d(256, 256, kernel_size=5, stride=1, padding=2)
self.conv4 = nn.Conv2d(256, 256, kernel_size=7, stride=1, padding=3)
self.conv5 = nn.Conv2d(256, 256, kernel_size=9, stride=1, padding=4)
self.conv6 = nn.Conv2d(256, 256, kernel_size=11, stride=1, padding=5)
def forward(self, x):
x = self.conv1(x)
x = self.conv2(x)
x = self.conv3(x)
x = self.conv4(x)
x = self.conv5(x)
x = self.conv6(x)
return x

结论:elementwise conv(1x1 conv)的虽然较少了计算量,但是计算密度也 很低。随着kernel size增大,计算密度增长率逐渐下降
output size对计算密度的影响
from torchstat import stat
import torch
import torch.nn as nn
class UpsampleConvNet(nn.Module):
def __init__(self):
super(UpsampleConvNet, self).__init__()
# 假设初始输入尺寸为7x7, 通过上采样逐步增加特征图大小
self.conv1 = nn.Conv2d(256, 256, kernel_size=3, stride=1, padding=1)
# 上采样层,用于增加特征图的维度
self.upsample = nn.Upsample(scale_factor=2, mode='nearest')
self.conv2 = nn.Conv2d(256, 256, kernel_size=3, stride=1, padding=1)
self.conv3 = nn.Conv2d(256, 256, kernel_size=3, stride=1, padding=1)
self.conv4 = nn.Conv2d(256, 256, kernel_size=3, stride=1, padding=1)
self.conv5 = nn.Conv2d(256, 256, kernel_size=3, stride=1, padding=1)
self.conv6 = nn.Conv2d(256, 256, kernel_size=3, stride=1, padding=1)
def forward(self, x):
x = self.conv1(x)
x = self.upsample(x) # 14x14
x = self.conv2(x)
x = self.upsample(x) # 28x28
x = self.conv3(x)
x = self.upsample(x) # 56x56
x = self.conv4(x)
x = self.upsample(x) # 112x112
x = self.conv5(x)
x = self.upsample(x) # 224x224
x = self.conv6(x)
return x
# 创建模型实例
model = UpsampleConvNet()
stat(model, (256, 7, 7))

结论:output size对计算密度的影响,随着output size变大,计算密度的增 长率逐渐下降
channel size对计算密度的影响
class CustomConvNet(nn.Module):
def __init__(self):
super(CustomConvNet, self).__init__()
# 定义卷积层
self.conv1 = nn.Conv2d(16, 32, kernel_size=3, stride=1, padding=1)
self.conv2 = nn.Conv2d(32, 64, kernel_size=3, stride=1, padding=1)
self.conv3 = nn.Conv2d(64, 128, kernel_size=3, stride=1, padding=1)
self.conv4 = nn.Conv2d(128, 256, kernel_size=3, stride=1, padding=1)
self.conv5 = nn.Conv2d(256, 512, kernel_size=3, stride=1, padding=1)
# 假设输入特征图大小为56x56,最后一层不改变通道数,仍然输出512通道
self.conv6 = nn.Conv2d(512, 512, kernel_size=3, stride=1, padding=1)
def forward(self, x):
x = self.conv1(x)
x = self.conv2(x)
x = self.conv3(x)
x = self.conv4(x)
x = self.conv5(x)
x = self.conv6(x)
return x

结论:channel size对计算密度的影响,越大的channel size计算密度 越高。
group convolution对计算密度的影响
class GroupConvNet(nn.Module):
def __init__(self):
super(GroupConvNet, self).__init__()
# 定义六个卷积层,卷积核大小均为3,组数依次为32, 16, 8, 4, 2, 1
self.conv1 = nn.Conv2d(32, 32, kernel_size=3, stride=1, padding=1, groups=32)
self.conv2 = nn.Conv2d(32, 32, kernel_size=3, stride=1, padding=1, groups=16)
self.conv3 = nn.Conv2d(32, 32, kernel_size=3, stride=1, padding=1, groups=8)
self.conv4 = nn.Conv2d(32, 32, kernel_size=3, stride=1, padding=1, groups=4)
self.conv5 = nn.Conv2d(32, 32, kernel_size=3, stride=1, padding=1, groups=2)
self.conv6 = nn.Conv2d(32, 32, kernel_size=3, stride=1, padding=1, groups=1) # 普通卷积
def forward(self, x):
x = self.conv1(x)
x = self.conv2(x)
x = self.conv3(x)
x = self.conv4(x)
x = self.conv5(x)
x = self.conv6(x)
return x

结论: group convolution对计算密度的影响。depthwise虽然降低了 计算量,但计算密度也下降的很多
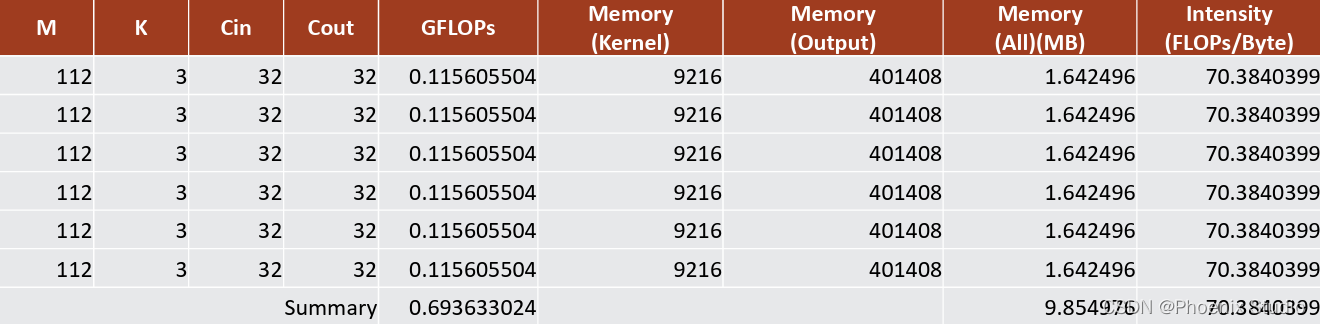
tensor reshape对计算密度的影响
-
计算量: M 2 ∗ K 2 ∗ C i n ∗ C o u t M^2*K^2*C_{in}*C_{out} M2∗K2∗Cin∗Cout
-
访存量 : ( K 2 ∗ C i n ∗ C o u t + M 2 ∗ C o u t ) ∗ 4 :(K^{2}*C_{in}*C_{out}+M^{2}*C_{out})*4 :(K2∗Cin∗Cout+M2∗Cout)∗4
M: 卷积核输出特征图的H和W。不同的时候可以用Mh,Mw表示
K:卷积核大小
- 模型中没有
tensor reshape
- 模型中有3个
tensor reshape
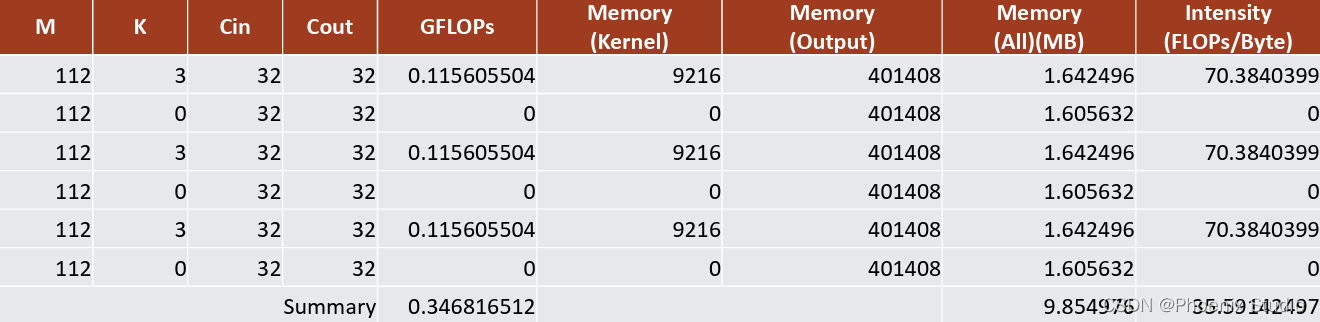
- 模型中有5个
tensor reshape
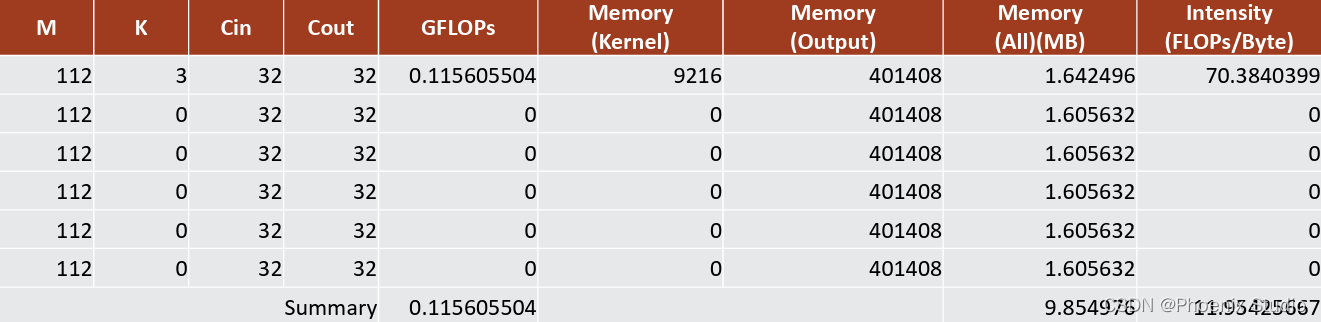
结论:过多的tensor reshape会降低模型的计算密度
全连接层对计算密度的影响
- 计算量: C i n ∗ C o u t C_{in}*C_{out} Cin∗Cout
- 访存量:( C i n ∗ C o u t ) ∗ 4 C_{in}*C_{out})*4 Cin∗Cout)∗4
M:卷积核输出特征图的H和W。不同的时候可以用Mh,Mw表示
K: 卷积核大小

对单个模型构建Roofline Model
- 以ResNet18为例
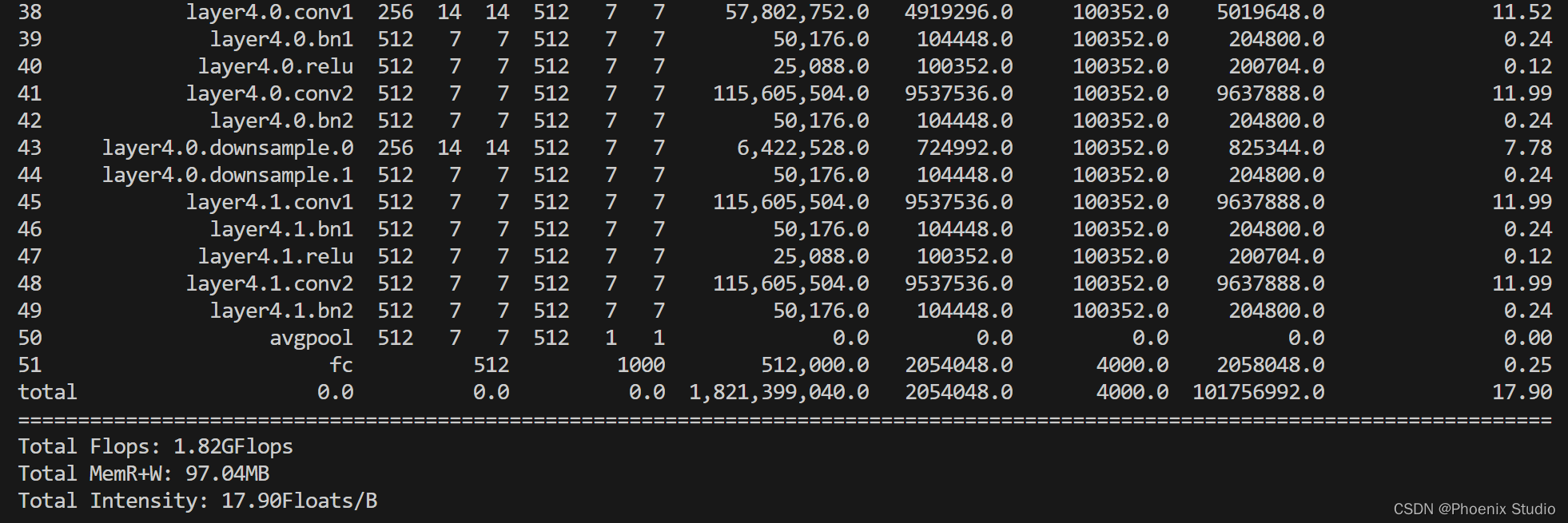
也可以使用Nsight Compute,可以查看各个kernel的roofline model(当前的实际值而非理论值)和整个模型的roofline model十分的方便。
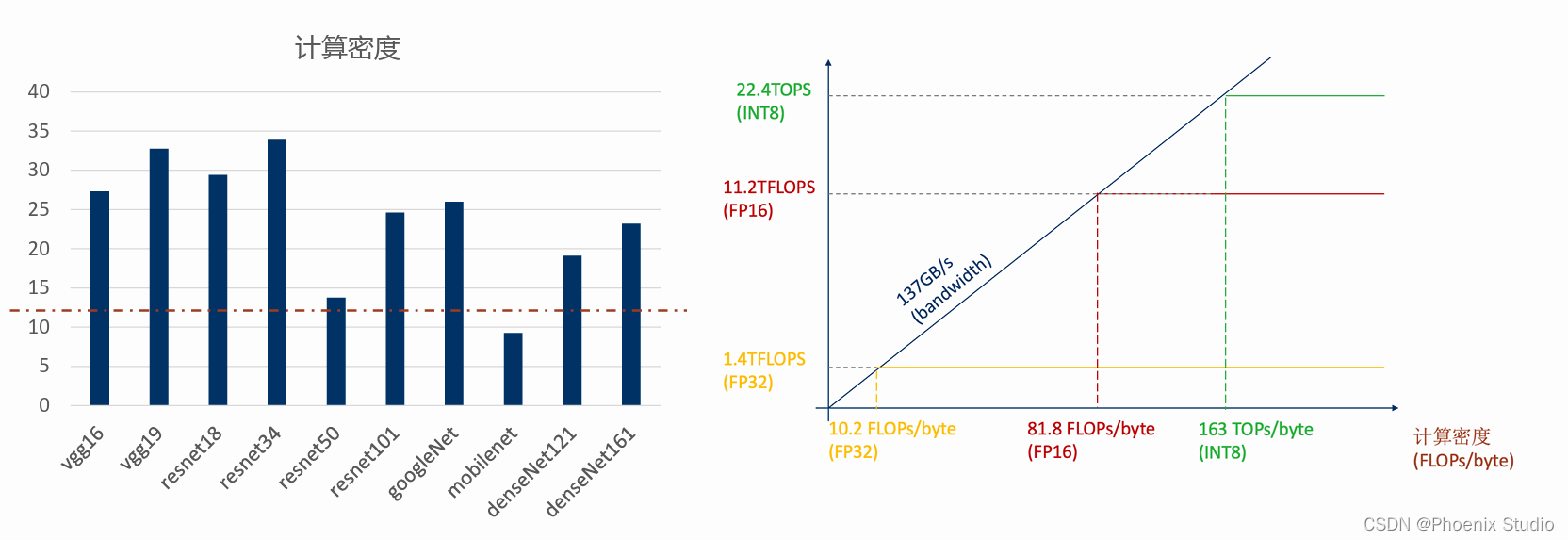
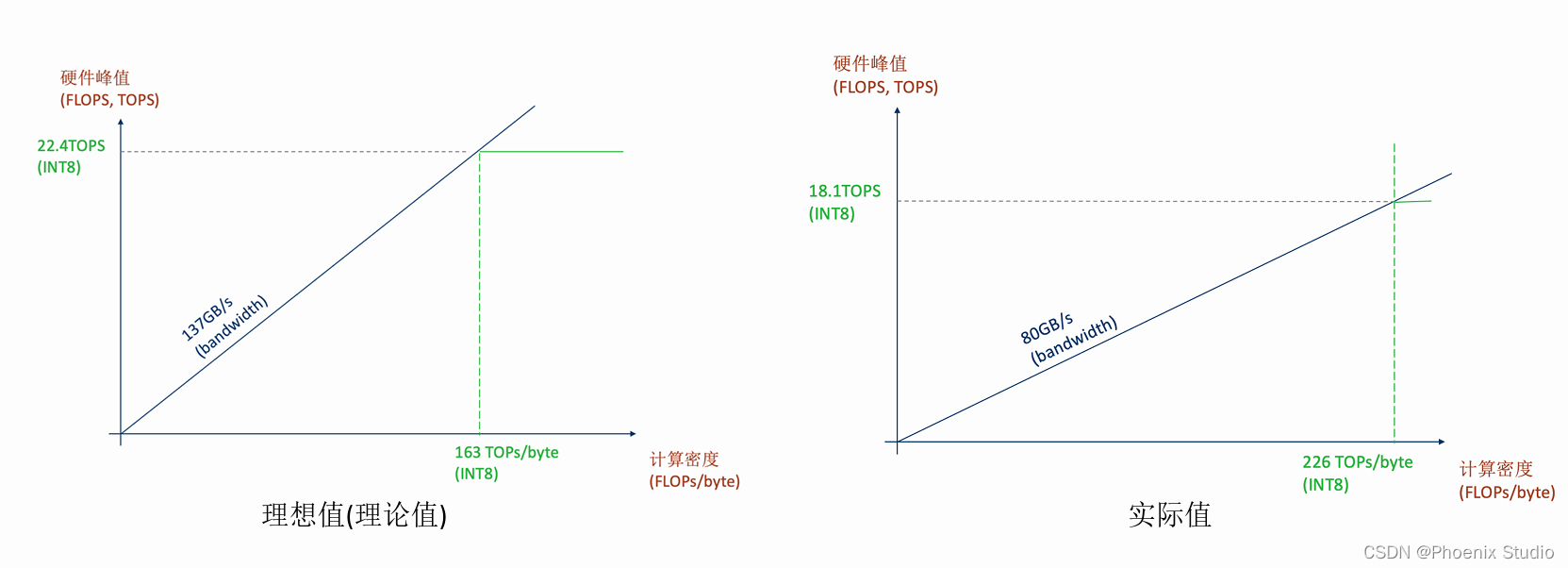
Jetson AGX Xavier架构中FP32的计算在10.2FLOPs/byte就计算饱和。所以这些模型 其实都理论上已经计算饱和
到目前讲的是理论值。然而实际上我们会发现:
- 峰值可能会小于22.4TOPS
- bandwidth可能会小于137GB/s 需要根据一系列benchmark找到部署架构的真实值。(比如自己写几个计算密集的核函数或者你不想自己写可以康康这个大佬的repo:https://github.com/ekondis/gpumembench)
Nsight Compute⼯具⾃动搭建roofline Model
⼀般最后跟的代码是可执⾏⽂件,如果是python代码,就需要在前⾯加上编译器的⼆进制⽂件的完整路径,正确的⽰例如下:
ncu --set roofline -o profile_roofline --target-processes all xxx\python.exe xxx.py
不加编译器路径会报以下错误:
==ERROR== The target application is not an executable binary.
==ERROR== If the target application is a script, try prepending the full path to the interpreter binary.
注意:需要以管理员权限运行该条命令,不然会报错:
==ERROR== ERR_NVGPUCTRPERM - The user does not have permission to access NVIDIA GPU Performance Counters on the target device 0. For instructions on enabling permissions and to get more information see https://developer.nvidia.com/ERR_NVGPUCTRPERM
上述命令执行后将会生成文件profile_roofline.ncu-rep,通过Nsight Compute软件打开(这里同样用ResNet34,输入大小为(33232)进行测试)
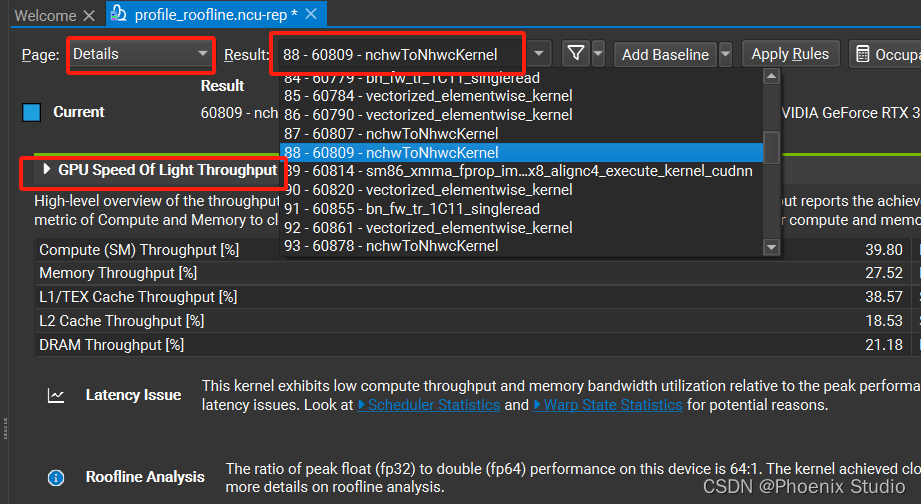
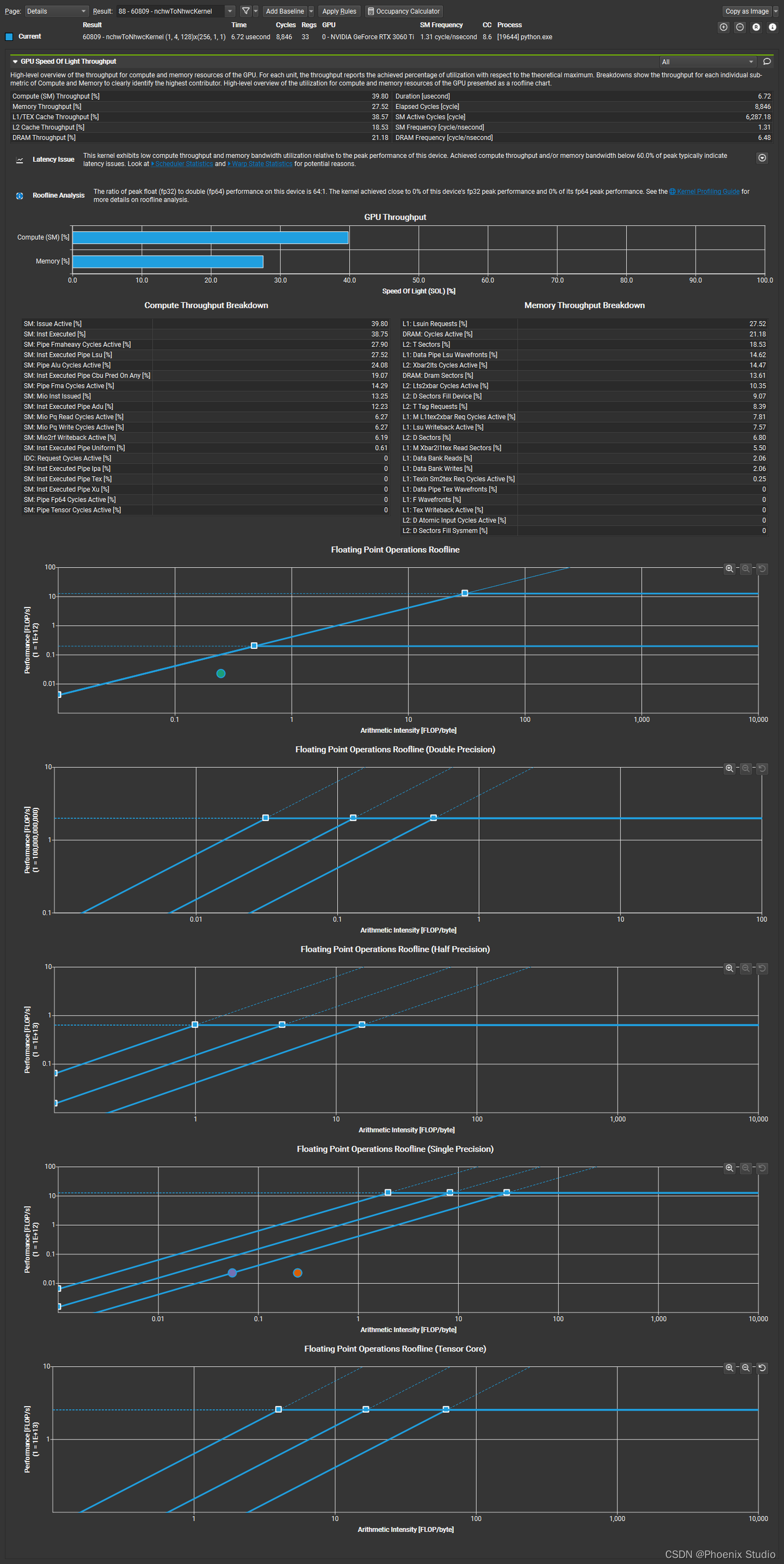
选择展示Details页面,选择某一个kernel,然后展开GPU Speed Of Light Throughput选项,就可以看到该kernel的详细统计信息(下图中的Double Precision、Half Precision 和Tensor Core Roofline中没有achived value小圆点是因为实际跑的算法模型数据值是单精度的,所以主要使用的是GPU中的FP32 Core,而FP64 Core、Tensor Core就没有使用到)。
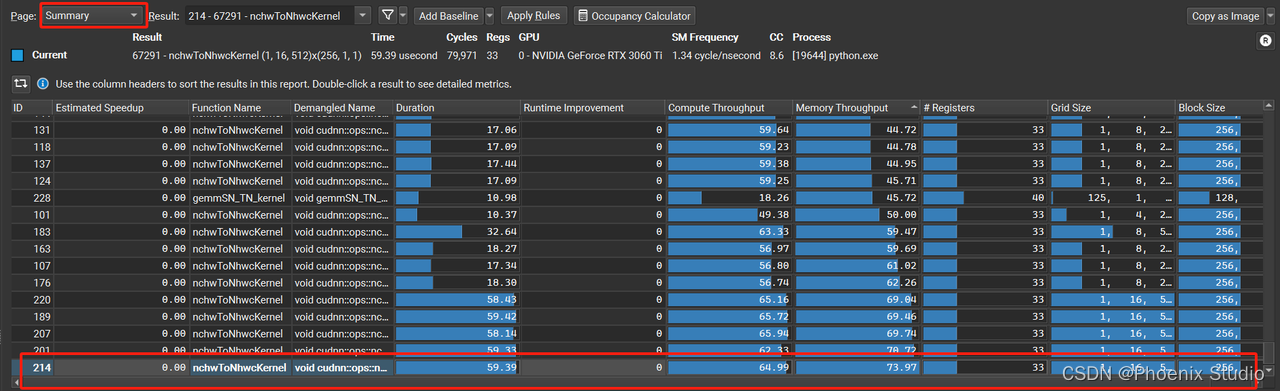
从summary中对所有kernel的统计概览来看(下图),各个kernel的计算量和内存使用率之间差别较大。
这里单独从内存占用率最高(73.97%)的一个双击进去为例,roofline模型图如下(peak work、peak traffic可以理解为该kernel运行过程中的最高算力值、最高使用的内存带宽,可见这两个参数的实际值小于官方公布的448.06GB/s),从图上可见实际表现值处于memory-bound区域,而稍微处于斜线下方,说明内存带宽上还没有完全利用完,利用率粗略计算为 39.724 / 0.13 203.148 / 0.48 = \frac{39.724/0.13}{203.148/0.48}= 203.148/0.4839.724/0.13= 72.2%与73.97%基本一致。
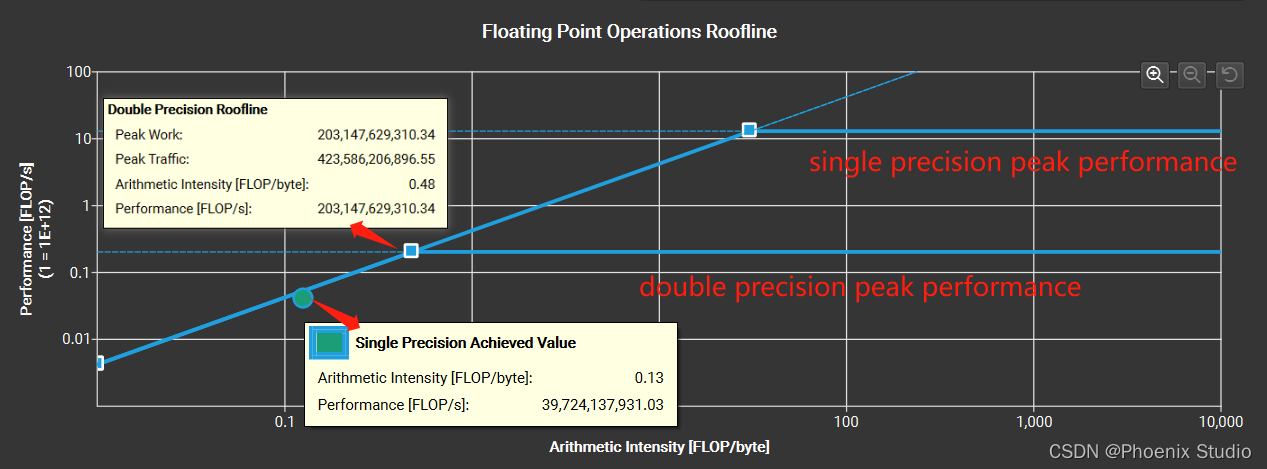
这里只是能看单独某一个kernel的roofline模型,要想要整个模型的效果,可以将所有kernel的各项值取平均在进行计算.
总结
Roofline模型可以帮助选择适合应用程序需求的硬件配置(GPU架构、核心数、频率),也可以依据特定的计算平台选择能最大化利用其算力资源的应用程序。
除此以外,还可以用于根据实际情况下所处的瓶颈区对应用程序进行性能优化。比如在深度学习网络模型中,当模型的计算强度小于平台的计算强度时,模型处于宽带瓶颈区,而为了最大程度发挥计算平台的性能,应尽量避免这种情况。
此时可以对模型结构进行优化或者增加带宽,在训练过程中,对其损失函数进行设计,比如当模型的计算强度低于计算平台的计算强度时,损失函数加上两个计算强度之间的差值再乘以某个系数(鼓励模型在训练过程中增加其计算强度,从而更充分地利用计算平台的算力资源)。这样训练过程中模型的计算强度就会往靠近计算平台的方向变化,从而达到目的。
参考
-
RooflineVyNoYellow.pdf (berkeley.edu)
-
Roofline Model与深度学习模型的性能分析 - 知乎 (zhihu.com)
-
Roofline模型的构建与应用 - 知乎 (zhihu.com)