ECC介绍
ECC
以下是针对瑞萨MCU的应用的ECC检测的详细分析。
当前公认安全有效的三大类公钥密钥体制分别为基于大数因子分解难题(RSA)、离散对数难题(DSA)和椭圆曲线离散对数(ECC)难题的密码体制。
保证RSA的安全性,则必须要增加密钥长度,所以我们可以看到RSA密钥从1024bit慢慢来到了4096比特。
由于汽车网络安全近几年才兴起,专为密钥存储设计的硬件资源有限,如果用RSA算法,密钥存储数量有限,而ECC(Elliptic Curve Cryptography)的出现有效弥补了这方面的缺憾,实现了密钥效率上的突破,根据NIST.SP.800-57pt1r5描述,对称算法和非对称算法的安全强度。
可以看到,160bits的ECC密钥长度实现的安全强度等同于RSA 密钥长度1024bits。
所以目前,汽车行业越来越倾向使用ECC来实现验签、会话密钥协商等。
RS-CANFD
在RS-CANFD中实现了ECC检查机制来检查RAM中数据的一致性。
RAM中的每个内存位置由39位组成。
其中32位用于存储用户数据;
7位用于存储用户数据。
对于存储ECC数据。对于每个长字(32位)内存位置,ECC数据是分配。
该ECC数据的值由ECC生成逻辑计算。
ECC校验机制对从CAN侧或CPU侧读访问时的数据进行校验RAM。如果检测到单个比特错误,则纠正它并在ECC状态寄存器中设置一个标志(寄存器在CAN IP之外)。
如果在传输扫描期间从CAN侧读取检测到多个比特错误,则发送在传输扫描下的CAN信道的请求将被抑制,并进行相应的处理寄存器。设置标志位。这样做是为了避免传输损坏的数据。
一般来说,如果检测到多个比特错误,则执行RAM测试以检查RAM状态。当没有
发现问题,切换到全局复位模式,然后进行通信初始化再一次。
如果ECC逻辑检测到错误,则RAM访问的错误地址将为
在捕获寄存器中捕获,该寄存器是ECC宏的一部分(不是RS-CANFD)。
ECC理解
密码学中的ECC校验通常指的是椭圆曲线密码学(Elliptic Curve Cryptography)中的校验过程。
在ECC中,校验通常涉及到使用公钥对消息进行数字签名,并使用签名验证算法来验证签名的有效性。ECC的数字签名方案通常基于椭圆曲线数字签名算法(ECDSA,Elliptic Curve Digital Signature Algorithm)或其他类似的算法。
简要来说,ECC校验的步骤通常包括以下几个阶段:
-
密钥生成:首先,生成一对公钥和私钥。公钥用于验证签名,私钥用于生成签名。
-
签名生成:发送方使用私钥对消息进行签名。这个过程通过特定的算法生成一个数字签名,该签名与消息相关联,且仅能由发送方的私钥生成。
-
签名验证:接收方使用发送方的公钥来验证签名的有效性。通过将签名、消息和公钥作为输入,利用签名验证算法来验证签名的正确性。如果验证成功,则可以确定消息的完整性和来源。
ECC的校验过程依赖于椭圆曲线的数学性质,使得它在相对较短的密钥长度下提供了与传统RSA等算法相当的安全性。
真正搞懂ECC,我们需要先了解椭圆曲线的概念和分类。
一般来讲,椭圆曲线是一个具体两个变量x、y的三次方程,满足
![]()
的所有点(x,y)的集合,以及一个无穷远点O(y趋于无穷)。
在不同域上,椭圆曲线的方程也有不同,所以还需要掌握实数域、有限域上的椭圆曲线方程。
椭圆曲线是平面解析几何学中的一种特殊曲线,其方程通常表示为:
[y^2 = x^3 + ax + b]
其中,(a) 和 (b) 是常数,并且 (4a^3 + 27b^2 \neq 0),这是为了保证曲线不存在奇点。在这个方程中,(x) 和 (y) 是变量,而 (a) 和 (b) 是参数。
椭圆曲线在密码学中有着广泛的应用,特别是在椭圆曲线密码学(Elliptic Curve Cryptography,ECC)中。在密码学中,椭圆曲线的方程通常在有限域上定义,例如在素数域上的椭圆曲线可以表示为:
[y^2 \equiv x^3 + ax + b \pmod{p}]
其中,(p) 是一个素数,(a) 和 (b) 是有限域上的常数。在密码学中,通常选择满足一些特定性质的椭圆曲线来进行加密和签名操作,例如,曲线上的点的阶(order)应该是一个大素数,以确保安全性。
椭圆曲线的一些特性使其成为密码学中的理想工具之一,包括:
-
抗量子计算攻击:相比传统的RSA等加密算法,椭圆曲线密码学提供了更高的安全性,对量子计算攻击更为抵抗。
-
小密钥尺寸:相比于传统的RSA算法,椭圆曲线密码学需要更小的密钥尺寸来提供相同的安全性,这使得它在资源受限的环境下更为适用。
-
高效性:椭圆曲线算法的加密、解密、签名和验证操作通常需要的计算量较小,因此更加高效。。
ECC原理
椭圆曲线真的不是一个椭圆
以实数域上的椭圆曲线为例,它是一条由方程
![]()
给定的曲线,a和b是常数,并满足
![]()
这与椭圆的方程
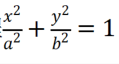
差别很大
那么为什么要叫椭圆曲线呢?
这是数学家在研究椭圆周长时,发现椭圆周长公式变换后可以得到
![]()
,因此椭圆曲线一直沿用至今。
椭圆曲线因为a、b的取值不同,在坐标系上有不同的形态
注意观察曲线,可以发现它们有两个明显共同点:
曲线关于X轴对称
任何非垂直X轴的直线与曲线至多三个交点
基于以上特性,我们来进行几何作图操作。
了解ECC
过曲线上的A和B作直线,得到与曲线相交的第三个点C,
过C做X轴的垂线得到C’’,这里我们定义A⊕B = C’’,读作A点加 B;
过A与C’’与曲线相较于D点D点有一个基于水平对称的点D’’,这里我们定义A ⊕C’’ = D’’,
如果我们继续用A去做点运算,可以轻易得到,A⊕D’’=E’’,依次类推。
那么假设我们已知起点A终点Z,请问这期间一共做了多少次点运算才能得到Z?
这就好像你在室内足球场踢球,朋友在外面等待,比赛结束后,你让朋友猜你一共踢了多少次皮球才得到1分,这显然是非常困难的。
有了这个思路,我们继续往下。
假设A点与曲线相切,这时候因为A和B是同一个点,所以公式 A⊕B = C’’,就变为了A⊕A = C’’,简写为C’’ = 2A:
注意这里的2A,不是简单的把坐标轴的值乘以2,而是计算曲线上的点,具体我在Desmos上的公式推导,这里不多赘述以免迷糊。
现在A与C’’再次连线,我们可以得到A⊕C’’ = A⊕2A = D’’,那么D’’ = 3A。
以此类推,我们可以得到最常见的标量运算公式:
P = kG
通过G点进行k次运算可以得出P,但反过来,如果只知道G和P,就很难求出k是多少。
因为P和Q都是椭圆曲线上的一个点,是坐标,k是整数;假设P = (-2,3),Q= (2,-6),要求出k是多少,这被公认是非常难的。
因此,我们可以把k作为私钥,G和P作为公钥。
PS:个人认为,作为使用者,ECC基本原理了解到这个程度即可,如果真要刨根问底,那得先从数学复习,建议从群论到有限域再到曲线推导。
ECC用法
ECC一般用于签名或者密钥协商。我们看看如何实现会话密钥协商:
Bob使用私钥b和公钥G生成结果B,并发给Alice;
Alice拿到公钥后,用私钥a和G生成结果A = aG,并发给Bob;
Bob拿到计算结果A,并用自己的私钥b与A生成新的密钥,bA = baG;
Alice拿到计算结果B,并用自己的私钥a与B生成新的密钥,aB = abG;
由于公式P = kG,k是整数,因此上述ba = ab。所以上述过程生成了只有Alice和Bob才知道的密钥,该密钥可用于会话的数据对称加解密。
即使攻击者拿到了G和B这些数据,由于私钥b\a的难以攻破(已知椭圆曲线上的起点和终点,求运算了多少次是非常难的),因此该方式也是比较安全。
ECC曲线
从上面的原理我们知道,要使用ECC进行数据加解密,最难得是建立起ECC曲线方程,所以现目前车规行业常用标准中推荐的椭圆曲线。
ECC寄存器
E710CTL — ECC Control Register
控制ECC模块的状态和模式。
可以读写使用16位或8位操作指令。
E710TMC — ECC Test Mode Control Register
一个16位寄存器,用于切换模式到测试模式和控制模式。
可以使用16位或8位操作指令进行读写。
E710TED — ECC Encoder and Decoder Data Test Register
用于ECC编码和解码的32位数据测试寄存器。
当可以使用32位操作指令对E710TED进行读写。
在测试模式下,可作为编码电路的数据输入和解码电路。
E710TRC — ECC Redundant Bit Data Control Test Register
一个32位测试寄存器,由四个字段组成,对应ECC的冗余位区。每个字段都可以作为8位寄存器访问名字都一样。有关每个字段的详细信息,请参阅这四个寄存器的描述。
当是读取;使用32位操作指令读取。
ECSYND — ECC Decoder Syndrome Data Register
是一个只读寄存器,用于确认解码电路产生的综合征码
处于测试模式。忽略对的写访问。
ECHORD — ECC 7-Bit Redundant Data Holding Test Register
保存了7位ECC冗余区域(上7位RAM数据),无法通过当外设模块在测试模式(ECTMCE)下访问RAM进行读取时
ECECRD — ECC Encoder Test Register
确认外设模块输入数据产生的冗余位。
这里,读取的数据是编码的结果(ECC[6:0]),而不是输出值。读取时,返回重置后的值。
ECERDB — ECC Redundant Bit Input and Output Substitution Buffer Register
E710EAD — ECC Error Address Register
一个只读寄存器,用于保存发生ECC错误的地址。
如果在启用ECC错误检测的情况下检测到ECC错误,则使用
检测信号作为触发器,并将地址存储在E710EAD中,作为ECC的地址错误发生。
当没有设置错误状态时,在检测到第一个ECC错误时存储该地址。但是,如果
1位错误后面跟着2位错误,后者的地址被存储。地址可以计算通过添加基址。
E710EAD中只能保存一个地址。
RTCAnSECC — RTCA Seconds Count Register
这个寄存器是秒计数器。它计数秒从00到59在BCD。
这个寄存器计数如下。
每次RTCAnSUBC子计数器溢出时触发。
如果子计数器溢出而秒计数器停止,
秒计数器的行为如下:
—当秒计数器停止时,如果有一个子计数器溢出,则保持溢出在内部。
秒计数器在重新启动时加1。
—当秒计数停止时,如果发生两次或两次以上溢出,则不能设置溢出计数
内部举行。
秒计数器在重新启动时加1。
—如果秒计数器被更新,而秒计数器停止,则子计数器溢出忽略了。
当数值从59变为00时,输出溢出信号。溢出信号触发分钟计数器。
流程 比较第一次和第二次读到秒计数器的值。当两者都是时,
相同的。如果没有,重复。
错误校验
瑞萨MCU内部有集成的ECC ;存储器集成ECC。ECC可以进行检测和校正
保存在内存中的数据的错误。ECC还可以检测和纠正错误
在ECC编码器和存储器之间产生;以及存储器和ECC解码器。
当除ECC外的1位纠错发生在指令取时,cache miss或
缓存无效,ECM错误源可能不会被通知,错误状态/错误地址寄存器可能不会被通知
更新。出现数据位和ECC位的所有0和1都不是合法的组合,并且被检测为2位错误。
可以同寄存器去配置几位进行校验;这样对于外部来说就是一个黑盒,实现完全的检测和保密。
可以设置纠错机制
这里的纠错机制包括
可以开启或关闭ECC错误检测和纠错功能。
启用后,可以选择以下任意一种设置。
·ECC纠错
进行检测和校正)。
·ECC纠错检测
当禁用时,既不进行错误检测也不进行错误纠正。
初始状态下,开启该功能;2位错误检测,1位错误检测和进行校正。
对于MCU中不同模块来说 会做不同模块的错误码 错误码可以进行校验去获取当前的故障错误。
另外还有ECC的使能和配置函数