同步时序电路的分析方法

基本步骤

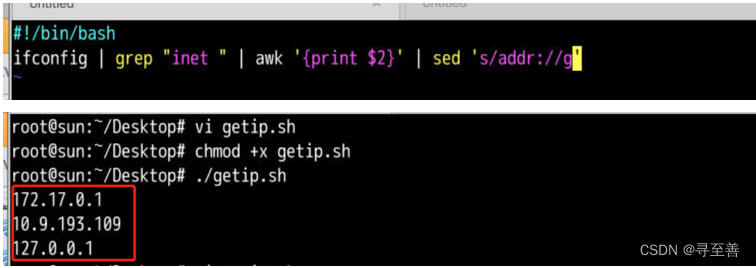
• Step1：写方程式

  时钟方程 ：各个触发器时钟信号的逻辑表达式，同步时序电路可省去不写

  输出方程：时序电路的输出逻辑表达式，通常为现态和输入变量的函数

  驱动方程 ：各触发器输入端的逻辑表达式

• Step2：求状态方程

  状态方程：将驱动方程代入相应触发器的特性方程所得到的方程

• Step3：根据状态方程列状态表

  状态表：将电路输入和现态的各种取值组合，代入状态方程和输出方程进行计算，求出相应的次态和输出

  注意：如现态的起始值已给定，则从给定值开始计算。如没有给定，则可设定一个现态起始值依次进行计算

• Step4：根据状态表画出对应的状态转换图 & 时序图

  状态转换图：指电路由现态转换到次态的示意图

  时序图：在时钟脉冲CP作用下，各触发器状态变化的波形图

• Step5：检查电路能否 “自启动”

  能自启动：存在无效状态，但没有形成循环

  不能自启动：存在无效状态，且形成了循环

• Step6：电路功能说明

  逻辑功能：根据状态表或状态转换图来说明电路逻辑功能

分析举例

【例】分析下图时序电路的逻辑功能

【解】这是时钟 CP 下降沿触发的同步时序电路，分析时不必考虑时钟信号；没有外部输入，只有输出，且输出仅与现态有关，属 Moore 型时序电路

• Step1：写方程式

  1. 驱动方程 （用现态表示）

     • $J_0=K_0=1$

       (若把 JK 触发器的输入端都接到高电平 1 ，就相当于把这个 JK 触发器转换成 T’ 触发器，那么 $CP$ 每来一个下降沿，$Q_0$ 和 $\overline{Q_0}$ 都会翻转一次)

     • $J_1=\overline{Q_2^n}\cdot Q_0^n$ ， $K_1=Q_0^n$

     • $J_2=Q_1^n\cdot Q_0^n$ ， $K_2=Q_0^n$

  2. 输出方程（用现态表示）

     $Y=Q_2^n\cdot Q_0^n$

• Step2：将驱动方程代入 JK 触发器的特性方程得到状态方程

  JK 触发器的特性方程：$Q^{n+1}=J\overline{Q^n}+\overline{K}{Q}^n$

  • $Q_0^{n+1}=J_0\overline{Q_0^n}+\overline{K_0}{Q}_0^n=1\cdot \overline{Q_0^n}+0\cdot Q_0^n=\overline{Q_0^n}$
  • $Q_1^{n+1}=J_1\overline{Q_1^n}+\overline{K_1}{Q}_1^n=\overline{Q_2^n}\cdot Q_0^n\cdot \overline{Q_1^n}+\overline{Q_0^n}\cdot Q_1^n$
  • $Q_2^{n+1}=J_2\overline{Q_2^n}+\overline{K_2}{Q}_2^n=Q_1^n\cdot Q_0^n\cdot \overline{Q_2^n}+\overline{Q_0^n}\cdot Q_2^n$

• Step3：根据状态方程列状态表

  现态的起始值没有给定，可设定一个现态起始值依次进行计算

  设电路初始状态为 $Q_2{Q}_1{Q}_0=000$

  

• Step4：根据状态表画出对应的状态转换图 & 时序图

  状态转换图说明

  

  状态转换图

  

  • 有效状态：被利用的状态（000、001、010、011、100、101），有效状态构成的循环称为“有效循环”

    

  • 无效状态：没有被利用的状态（110、111），无效状态若构成循环称为“无效循环”

  时序图（在时钟脉冲CP作用下，各触发器状态变化的波形图）

  

• Step5：检查电路能否 “自启动”

  电路虽然存在无效状态，但没有形成循环，所以电路能自启动。即使电路由于某种原因进入无效状态，只要给足够的脉冲，就能返回到有效循环

• Step6：电路功能说明

  逻辑功能：该电路能对 CP 脉冲进行六进制计数，并在端输出一个下降沿作为进位输出信号，为“同步六进制计数器”