摘要
我们利用保形推理,开发了回归中无分布预测推理的一般框架。所提出的方法允许使用回归函数的任何估计量构建响应变量的预测带。所得的预测带在标准假设下保留了原始估计量的一致性,同时保证了有限样本边际覆盖,即使这些假设不成立。我们从经验和理论上分析和比较了我们的共形框架的两个主要变体:完全共形推理和分裂共形推理,以及相关的折衷方法。这些方法在统计精度(结果预测间隔的长度)和计算效率之间提供了不同的权衡。作为扩展,我们开发了一种构造有效样本内预测区间的方法,称为秩一出共形推理,其计算效率与分裂共形推理基本相同。我们还描述了我们的程序的扩展,以产生具有局部变化长度的预测带,以适应数据中的异方差。最后,我们提出了一个变量重要性的无模型概念,称为遗漏一个协变量或LOCO推理。本文附带了一个R包conalinference,它实现了我们所介绍的所有建议。本着可重复性的精神,我们所有的经验结果也可以很容易地(重新)生成使用这个包。
论文:
Distribution-Free Predictive Inference For Regression
作者:卡内基梅隆大学统计学系
Jing Lei, Max G’Sell, Alessandro Rinaldo, Ryan J. Tibshirani, and Larry Wasserman
代码:https://github.com/ryantibs/conformal
保形推理。
我们考虑检验原假设Yn+1 = y,并根据增广样本(X1, Y1),…的经验分位数构造有效的p值。(Xn, Yn),(Xn+1, Yn+1),其中Yn+1 = y(详见下文第2节)。数据增强步骤使该过程免受过拟合的影响,因此所得到的预测带始终具有有效的平均覆盖范围,如(1)所示。在各种设置下,保形推理也作为批处理(而不是顺序)方法进行了研究。例如,Burnaev & Vovk(2014)考虑了低维最小二乘法和岭回归模型。Lei等人(2013)使用保形预测构建统计上接近最优的容忍区域。Lei和Wasserman(2014)将这一结果扩展到低维非参数回归。Lei(2014)探索了其他扩展,如分类和聚类;雷等人(2015)。共形预测框架最初是由Vovk等人(2005,2009)作为形成预测区间的顺序方法提出的。基本思想很简单。保留回归设置,并从P中给出一个新的独立绘图(Xn+1, Yn+1),以决定是否将值y包含在C(Xn+1)中。
在高维回归中,关于预测集的研究很少。Hebiri(2010)描述了保形套索估计量的近似。这种近似比建立在套索之上的原始共形预测方法有很大的加速,但首先失去了共形推理的关键吸引力——它不能提供有限样本覆盖。最近Steinberger & Leeb(2016)分析了一种在高维环境下的折衷预测方法,扩展了Butler & Rothman(1980)在低维回归中的结果。然而,只有当回归参数的基估计量满足强渐近均方误差和稳定性时,才能保证这种折衷方法具有渐近有效性。这将在2.4节中进一步讨论。在我们看来,一个简单,计算效率高,但似乎被忽视的强大方法是分裂共形推理(见Lei et al. (2015);Papadopoulos et al.(2002),或章节2.2)。例如,当与套索估计器结合使用时,形成分裂共形预测区间的总成本主要由套索拟合的成本决定,并且无论套索估计器是否一致,该方法总是在任何设置下提供有限样本覆盖。
高维推理。在高维推理领域,最近有一个非常令人兴奋的研究方向,是关于**(固定的)基于群体的目标或(随机的)后选择目标的置信区间的构建**。在第一类基于总体的方法中,假设线性模型为真,重点是为该模型中的系数提供置信区间(参见,例如,Belloni et al. (2012);Buhlmann (2013);Zhang & Zhang (2014);van de Geer et al. (2014);Javanmard & Montanari(2014))。在第二类,后选择方法中,重点是在给定选定协变量子集的最佳线性近似中覆盖系数(参见,例如,Berk等人(2013);Lee et al. (2016);Tibshirani等人(2016);Fithian et al. (2014);田&泰勒(2015a,b))。这些推理方法都很有趣,它们服务于不同的目的(即,两个类背后的目的是不同的)。然而,一个共同的线索是,所有这些方法都依赖于非平凡的假设——即使不需要假设线性模型为真,条件通常(在不同程度上)取决于所考虑的回归估计器的质量、误差分布误差方差的知识或可估计性,误差的均方差等。相比之下, 我们在第6节中描述了两种基于变量重要性的预测方法完全不依赖于这样的条件。
大纲
在本文中,我们对回归中的保形推理做出了一些方法和理论上的贡献。
-
我们提供了保形推理(第2节)的一般介绍,保形推理是构造无分布、有限样本预测集的通用工具。我们特别考虑了高维回归的背景,因为现有的推理方法需要很强的假设,因此可以认为共形推理是最有用的场景。
-
我们为共形推理提供了新的理论见解:其有限样本覆盖的准确性保证(定理2.1,2.2),以及无分布的渐近样本覆盖保证(定理2.3,5.1)。
-
我们还证明了保形推理的版本近似于某些oracle方法(第3节)。在这样做的过程中,我们在标准假设下提供了预测区间长度的近最优界限。具体来说,我们将展示以下内容。
-
- 1 如果基估计量在重采样和小扰动下是稳定的,则保形预测带接近依赖于估计量的oracle带(定理3.2,3.3)。
-
- 2 如果基估计量一致,则保形预测带接近于所有有效预测带中长度最短的超级预言带(定理3.4,3.5)。
-
我们进行了广泛的模拟研究(第4节),以评估共形推理的两种主要变体:完整和分裂共形方法,以及相关的折刀方法。这些模拟可以使用我们附带的R包conformal Inference 来重现,它提供了本文中研究的所有方法的实现(包括下面描述的扩展和变量重要性度量)。
-
我们开发了保形推理的两个扩展(第5节),允许更多信息和灵活的推理:具有样本内覆盖的预测区间和具有不同局部长度的预测区间。
-
我们提出了两种新的、无模型的、基于预测的方法来推断基于留一个协变量或LOCO推理的变量重要性(第6节)。
保形推理
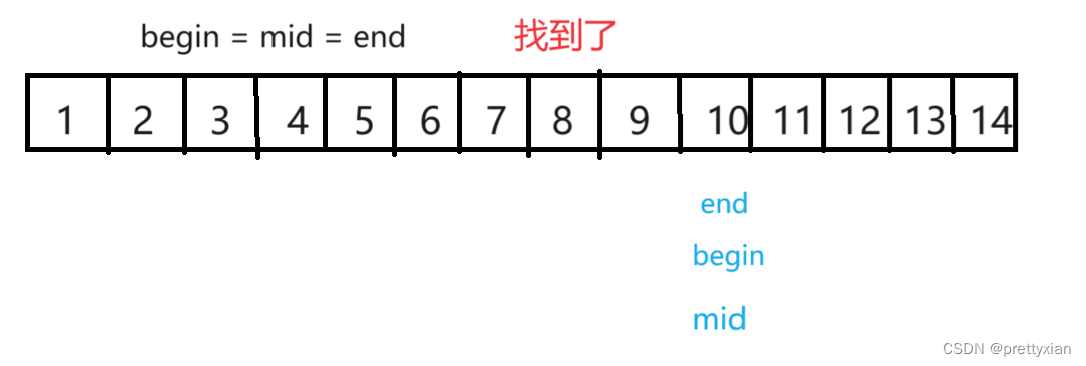
适形预测理论背后的基本思想与样本分位数的一个简单结果有关。让U1,…,一个标量随机变量的iid样本(实际上,后面的参数在i - id假设被较弱的互换性假设所取代后仍然成立)。对于给定的错误覆盖水平α∈(0,1),以及另一个iid样本Un+1,请注意
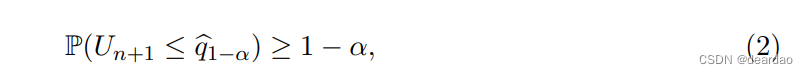
其中我们基于U1定义样本分位数
q
1
−
α
q_{1−α}
q1−α为
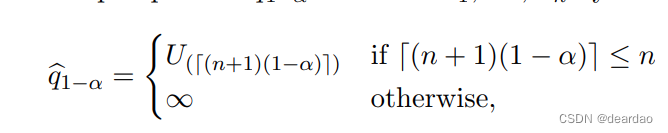
U(1)≤…≤U(n)表示U1的阶统计量,…,联合国。(2)中的有限样本覆盖性质很容易验证:通过互换性,Un+1在U1、…, Un, Un+1均匀分布在集合{1,…, n + 1}。
在我们的回归问题中,我们观察到i.i.d样本Zi = (Xi, Yi)∈R d × R ~ P, i = 1,…, n时,我们可以考虑以下朴素的方法来构造Yn+1在新特征值Xn+1处的预测区间,其中(Xn+1, Yn+1)独立于p
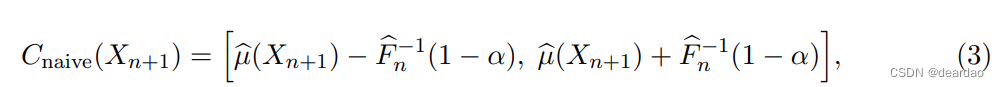
其中µ是底层回归函数的估计量,Fn是拟合残差的经验分布|Yi−µb(Xi)|, i = 1,…, n和Fb−1 n(1−α)为Fbn的(1−α)分位数。如果估计的回归函数µ是准确的(即,足以使拟合残差分布的估计(1−α)分位数Fn(1−α)接近总体残差的(1−α)分位数|Yi−µ(Xi)|, i = 1,…),这对于大样本是近似有效的。保证µ的这种精度通常需要适当的规则条件,包括底层数据分布P和估计器µ本身,例如正确指定的模型和/或适当选择调优参数。
保形预测集
一般来说,由于拟合的残差分布经常向下偏置,因此朴素方法(3)可以严重掩盖。保形预测区间(Vovk et al., 2005, 2009;Lei et al., 2013;Lei & Wasserman, 2014)克服了原始区间的缺陷,并且,在某种程度上值得注意的是,保证提供适当的有限样本覆盖,而不需要对P或µ进行任何假设(除非µb是数据点的对称函数)。
考虑以下策略:对于每个值y∈R,我们构造一个增广回归估计量µ_y,它是在增广数据集Z1,…上训练的。Zn (Xn+1, y)现在我们定义
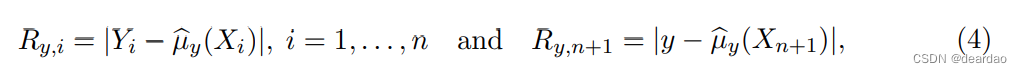
并将Ry,n+1在剩余的拟合残差Ry,1,…中排序。, Ry,n,计算
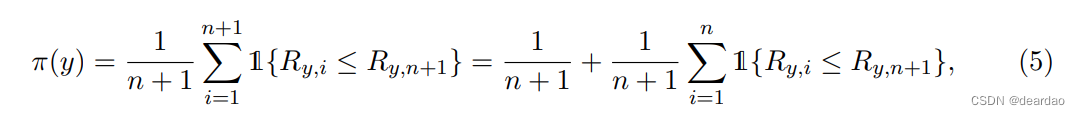
增广样本中拟合残差小于上一个的点的比例,Ry,n+1。这里1{·}是指示器函数。通过数据点的可交换性和µb的对称性,当y = Yn+1时,我们看到构造的统计量π(Yn+1)均匀分布在集合{1/(n +1), 2/(n +1),…, 1},这意味着
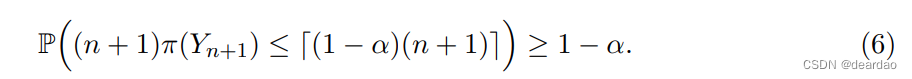
我们可以把上面的显示解释为说1−π(Yn+1)为检验零假设H0: Yn+1 = y提供了一个有效的(保守的)p值。
通过对y∈R的所有可能值进行逆检验,根据性质(6),我们立即得到在Xn+1处的适形预测区间,即
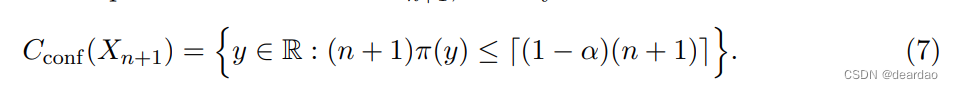
(4)、(5)、(7)中的步骤必须在每次我们想要产生一个预测区间(在一个新的特征值上)时重复。在实践中,我们还必须将(7)中的注意力限制在一个由试验值y组成的离散网格上。为了完整起见,这在算法1中进行了总结。
通过构造,式(7)中的共形预测区间具有有效的有限样本覆盖;这个间隔也是准确的,这意味着它不会实质上覆盖过多。这些归纳为以下定理,其证明见附录A.1。
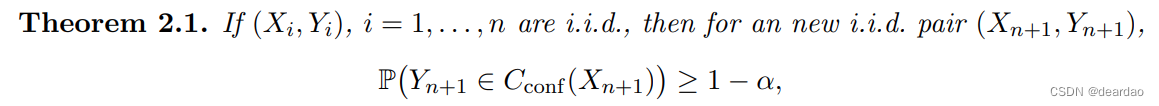

Remark 1。定理的第一部分,关于回归中保形区间的有限样本有效性,是所有保形推理过程的标准性质,是由Vovk提出的。第二部分——共形区间的反保守性——是新的。仅对于第二部分,我们要求残差具有连续分布,这是一个相当弱的假设,用于在(绝对)残差排序时避免联系。通过使用随机平局规则,可以完全避免这种假设。在实践中,适形层的覆盖高度集中在1−α附近,这一点在第4节的实验中得到了证实。除了连续性假设外,定理2.1中不需要关于回归估计量µ或数据生成分布p的假设。这是保形推理的一个值得注意和独特的性质,对于在2.4节中讨论的折刀方法(或者,对于用于在高维线性模型中产生系数置信区间的方法)是不成立的。
Remark 2。一般来说,当我们改进底层回归函数µ的估计量µb时,得到的适形预测区间的长度会减小。直观地说,这是因为更精确的µb导致更小的残差,而保形区间本质上是由(增广的)残差分布的分位数定义的。第4节给出了支持这一直觉的实证例子。
Remark 3。定理2.1中的概率命题取i.i.d个样本(Xi, Yi), i = 1,…, n, n + 1,因此它们断言平均(或边际)覆盖率保证。这不应该与P(Yn+1∈C(x)| Xn+1 = x)≥1−α(对于所有x∈R d)相混淆,即条件覆盖,这是一个更强的性质,不能通过有限长度预测区间来实现,而不需要对模型和估计器进行正则性和一致性假设(Lei & Wasserman, 2014)。条件覆盖在某些条件下是渐近成立的;参见第3节定理3.5。
Remark 4。定理2.1仍然成立,如果我们用
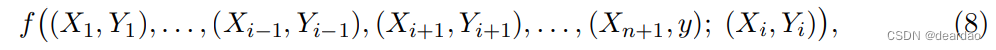
其中f是前n个参数对称的任意函数。在适形推理中,这样的函数f称为符合性分数。例如,(8)中的值可以是在(Xi, Yi)处求值的估计联合密度函数,也可以是在(Xi, Yi)处求值的条件密度函数(后者相当于Y−E(Y |X)独立于X时的绝对残差Ry,i,并且在[0,∞)上具有密度递减的对称分布)。我们将在第5.2节中讨论一个特殊的局部加权合格评分。
Remark 5。我们通常使用术语“无分布”来指代有限样本覆盖属性,假设只有iid数据。虽然保形预测仅在iid假设下为所有分布和所有对称估计提供了有效的覆盖,但保形区间的长度取决于初始估计量的质量,并且在第3节中我们提供了关于这种关系的理论见解。

2.2 分裂保形预测集
上一节研究的原保形预测方法计算量大。对于任意Xn+1和y,为了判断y是否包含在Cconf(Xn+1)中,我们在增广数据集(包括新点(Xn+1, y))上重新训练模型,并重新计算和重新排序绝对残差。在某些应用中,Xn+1不一定被观察到,预测区间是通过在一个精细网格上对(x, y)的所有对上评估1{y∈Cconf(x)}来构建的,如算法1所述。在核密度估计和核回归的特殊情况下,Lei et al.(2013)描述了对完整保形预测集的简单而准确的近似;雷和沃瑟曼(2014)。在低维线性回归中,Sherman-Morrison更新方案可以通过节省每次改变查询点(x, y)时求解全线性系统的成本来降低全保形方法的复杂性。但在高维回归中,我们可能会使用相对复杂的(非线性)估计器,如lasso,执行有效的完全共形推理仍然是一个开放的问题.
幸运的是,有一种替代方法,我们称之为拆分保形预测,它是完全通用的,其计算成本只是完全保形方法的一小部分。分割保形法采用样本分裂的方法将拟合步骤和排序步骤分离,其计算量仅为拟合步骤的计算量。类似的观点也出现在在线预测文献中,被称为归纳共形推理(Papadopoulos et al., 2002;Vovk et al., 2005)。算法2中总结的分割共形算法改编自Lei et al.(2015)。它的键覆盖性质在定理2.2中给出,在附录A.1中得到证明。(在这里,以及以后讨论分裂共形推理时,为了简单起见,我们假设样本量n是偶数,因为当n为奇数时只需要非常小的变化。
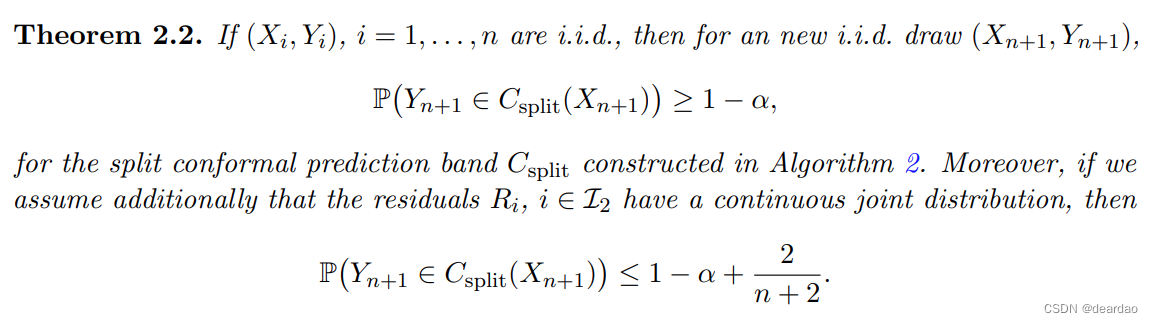
与原始的保形方法相比,拆分保形推理除了效率极高之外,在内存需求方面也具有优势。例如,如果回归过程A(在算法2的符号中)涉及变量选择,如套索回归或前向逐步回归,那么我们只需要在评估新点Xi, i∈I2的拟合并计算残差时存储选择的变量,用于排序步骤。当原始变量集非常大,而选择的变量集要小得多时,这可以大大节省内存。
分裂共形预测区间也提供了一个近似的样本内覆盖保证,使它们更容易说明和解释使用给定的样本(Xi, Yi), i = 1,…, n,无需获得未来的抽奖。下面将对此进行描述
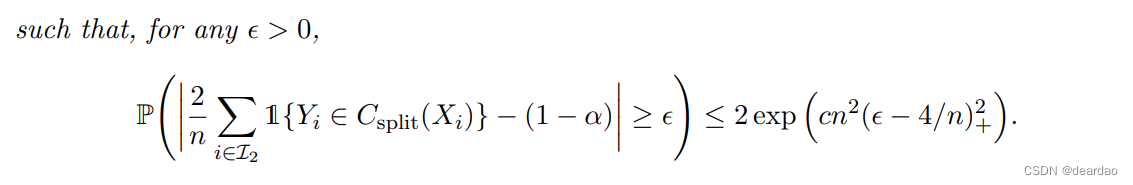


![[Cpp]类和对象 | 实现日期类](https://img-blog.csdnimg.cn/direct/ba4e5f8af0ac441d9320898b60730aeb.png)