【算法】-- 二分查找详注

news2024/11/18 9:27:01

引入

二分查找，也称为折半查找；首先，二分查找是一种基于有序数组中查找特定元素的算法，所以它会因为数组的一些特性而受限。它的工作原理是不断将要查找的区间分成两部分，然后确定目标值可能存在的区间，直到找到目标值或者确定目标值不存在为止。这个算法的时间复杂度为O(log n)，其中n是数组的大小。二分查找通常比线性查找（暴力查找）快，尤其是在大型数组中查找元素时。

时间复杂度

相比于暴力求解，二分查找大幅提高了查找的效率。在中国14亿人中，用二分查找算法找一个人最多只需要31次。二分查找大大地提升了程序运行的效率。

计算时间复杂度：

数组的元素个数为N，每查找一次，数组元素减半，数组元素个数依次递减为N / 2，N / 4，N / 8 ...... 。

那么反过来，2 * 2 * 2 * 2 .......2 = N 。假设一共有x个2 ，那么x就等于 log以2为底N的对数，所以二分查找的时间复杂度为O(logN)。

图解示例

接下来我用一个具体的例子来阐释二分查找的逻辑，取一个定长的数组，查找数据10。

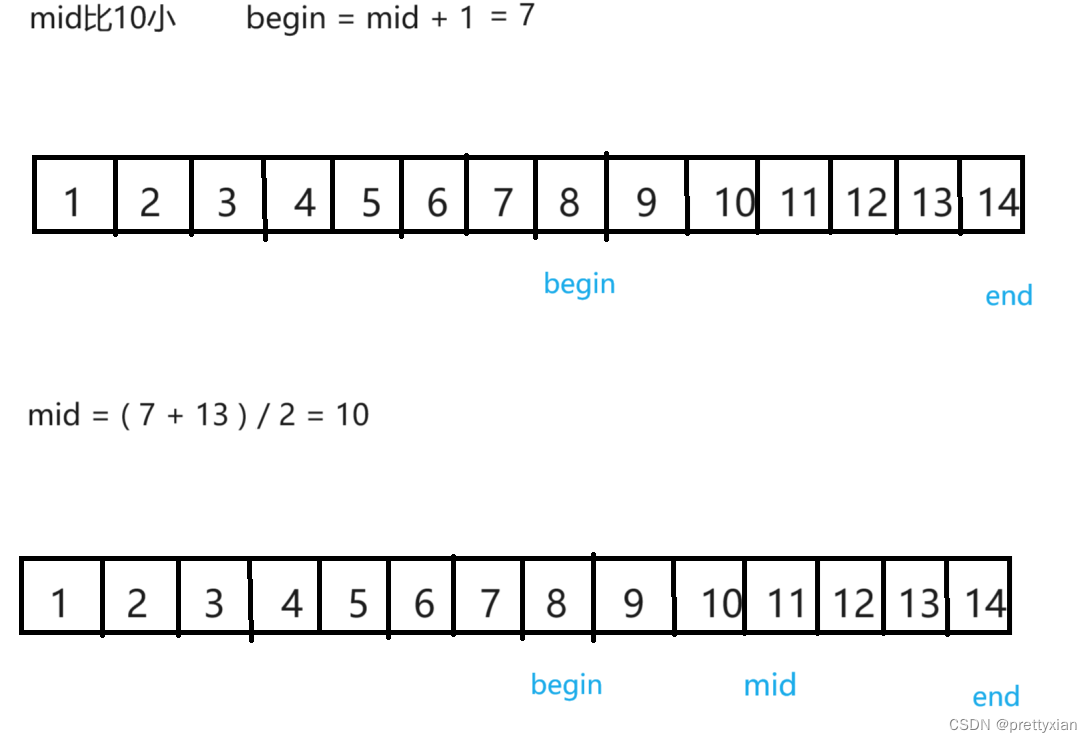
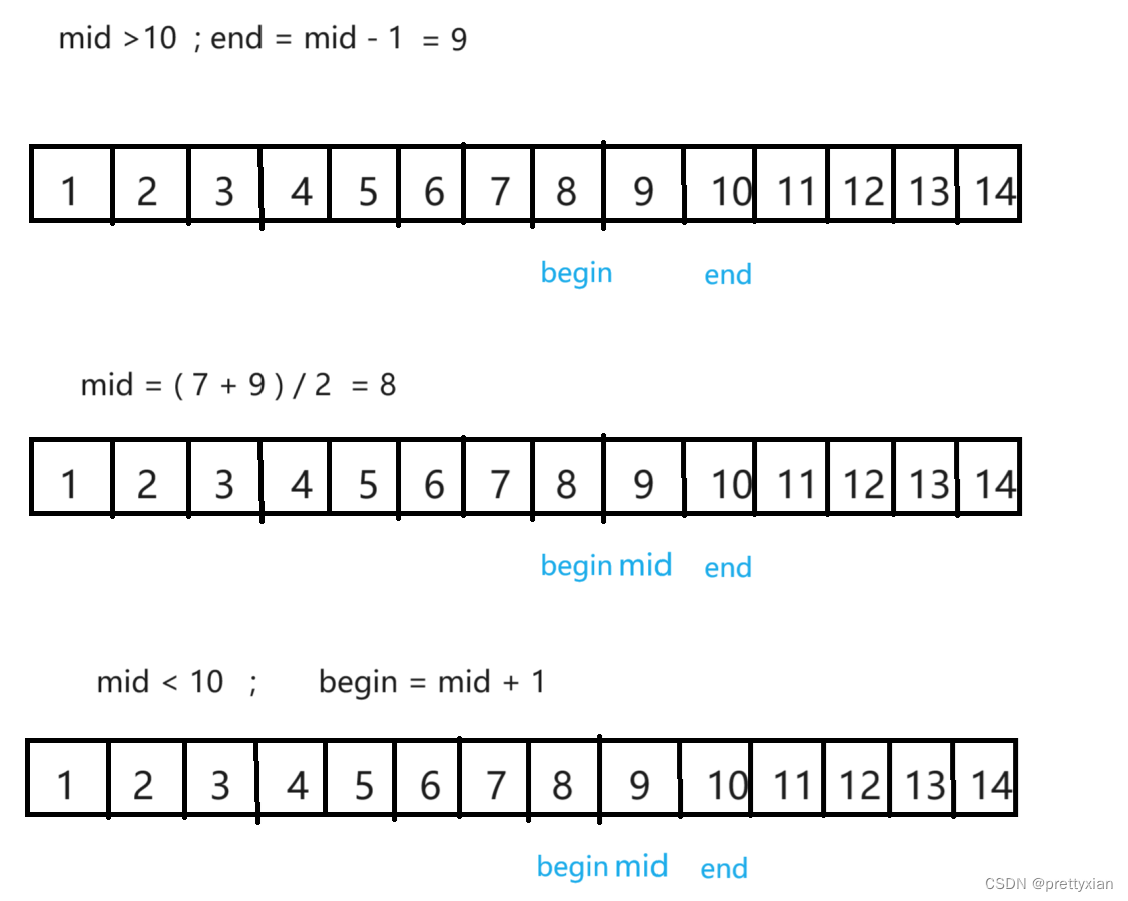
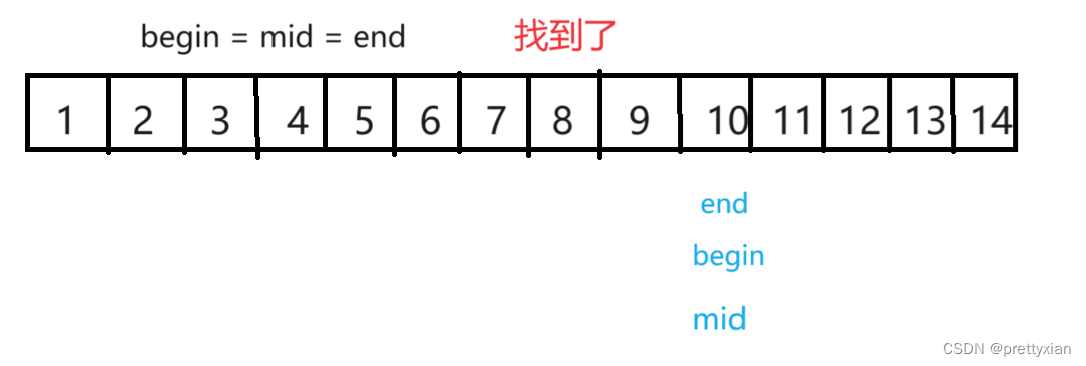
区间讨论

二分查找本质上是在区间上进行查找，区间可以取左闭右开，也可以取左闭右闭；循环的条件可以是while(left < right),也可以是 while(left <= right)

循环的条件是while(left <= right)

那么当左右相等时，因为左右都取的闭区间，还要进行依次查找。

循环的条件是while(left < right)

这个时候，当左右相等时，因为是左闭右开区间，区间内已经没有数了，循环结束。

左闭右开：

#include <stdio.h>

int binary_search(int arr[], int size, int target) {
    int left = 0;
    int right = size;  // 注意右边界是数组大小而不是数组大小减一

    while (left < right) {
        int mid = left + (right - left) / 2;  // 计算中间索引

        if (arr[mid] == target) {
            return mid;  // 找到目标值，返回索引
        } else if (arr[mid] < target) {
            left = mid + 1;  // 目标值在右侧
        } else {
            right = mid;  // 目标值在左侧，注意右边界不减一
        }
    }

    return -1;  // 未找到目标值
}

int main() {
    // 测试数据
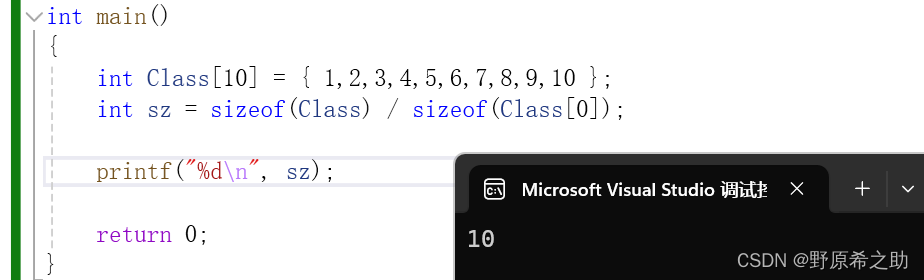
    int arr[] = {1, 3, 5, 7, 9, 11, 13, 15, 17};
    int size = sizeof(arr) / sizeof(arr[0]);  // 计算数组大小

    int target = 9;  // 目标值

    int result = binary_search(arr, size, target);

    if (result != -1) {
        printf("目标值 %d 在数组中的索引为 %d\n", target, result);
    } else {
        printf("目标值 %d 不存在于数组中\n", target);
    }

    return 0;
}

左闭右闭：

#include <stdio.h>

int binary_search(int arr[], int size, int target) {
    int left = 0;
    int right = size - 1;

    while (left <= right) {
        int mid = left + (right - left) / 2;  // 计算中间索引

        if (arr[mid] == target) {
            return mid;  // 找到目标值，返回索引
        } else if (arr[mid] < target) {
            left = mid + 1;  // 目标值在右侧
        } else {
            right = mid - 1;  // 目标值在左侧
        }
    }

    return -1;  // 未找到目标值
}

int main() {
    // 测试数据
    int arr[] = {1, 3, 5, 7, 9, 11, 13, 15, 17};
    int size = sizeof(arr) / sizeof(arr[0]);  // 计算数组大小

    int target = 9;  // 目标值

    int result = binary_search(arr, size, target);

    if (result != -1) {
        printf("目标值 %d 在数组中的索引为 %d\n", target, result);
    } else {
        printf("目标值 %d 不存在于数组中\n", target);
    }

    return 0;
}