神经网络算法 :一文搞懂 Encoder-Decoder(编码器-解码器)_有编码器和解码器的神经网络-CSDN博客这篇文章写的不错,从定性的角度解释了一下,什么是编码器与解码器,我再学习+笔记补充的时候,讲一下原理+代码实现。
简单来说 编码器就是把抽象问题转化为计算机能识别计算的数学问题
解码器就是将计算机计算好的数学问题转化成为最终结果能看懂的形式
以下是一个不错的PPT图
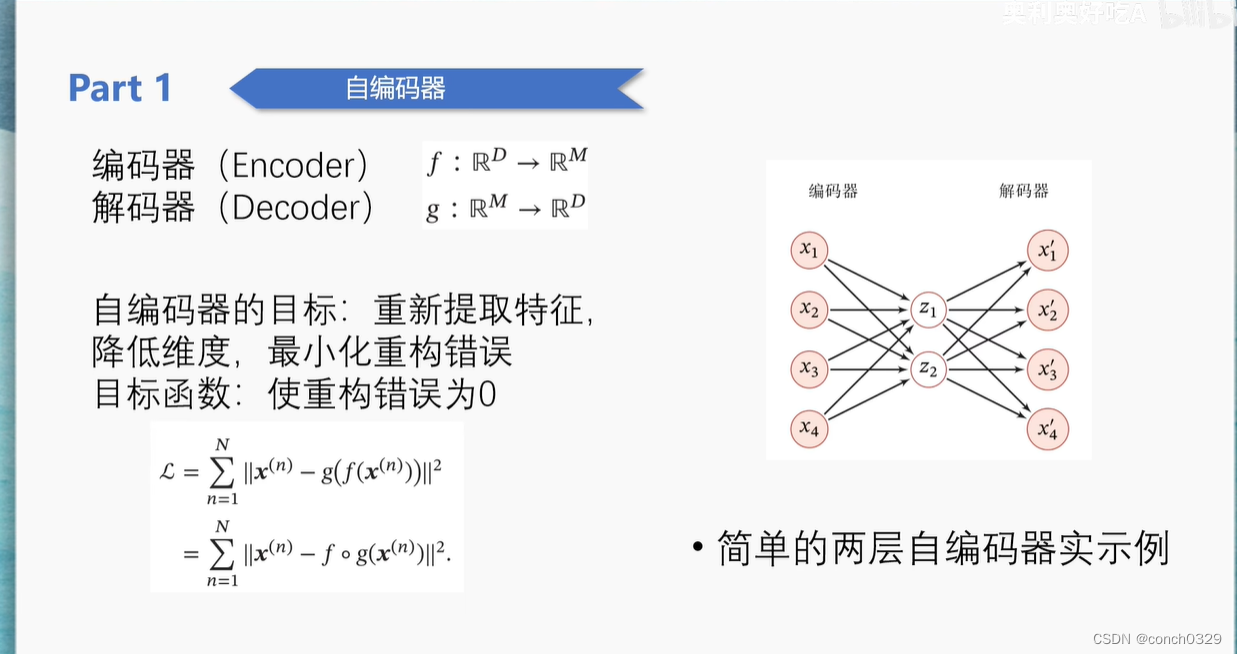
1.先讲一下Encoder吧
参考的是这个学习的链接
【Transformer系列(1)】encoder(编码器)和decoder(解码器)_encoder和decoder的区别-CSDN博客
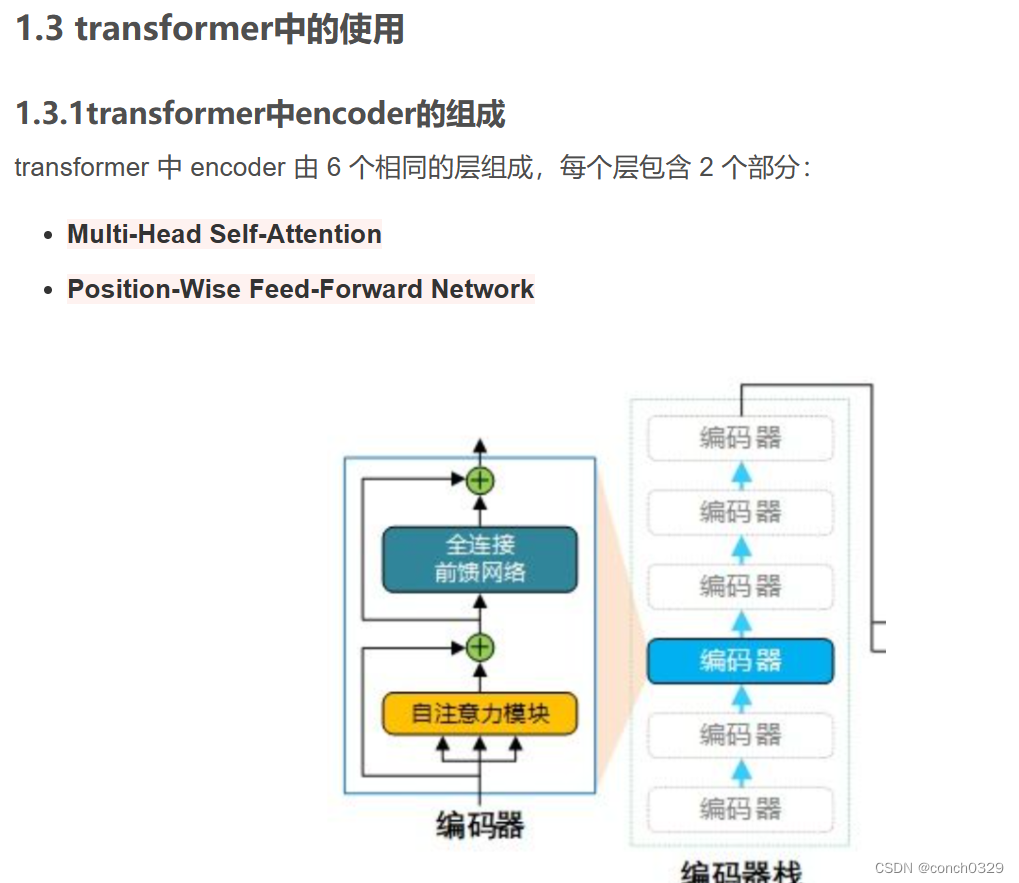
encoder的构成主要有这么几块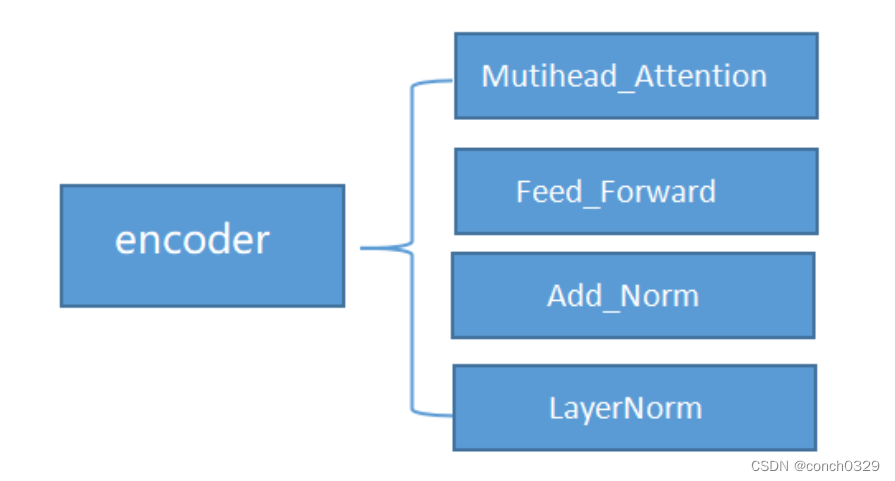
图1encoder的包括图
代码我也直接拿原作者的了,我在pycharm中跑了一下,具体列出并学习我不会的地方
import torch
import torch.nn as nn
from torch.nn.functional import softplus
from torch.nn import functional as F
class encoder(nn.Module):
def __init__(self):
super(Encoder,self).__init__()
self.positional_encoding = Positional_Encoding(config.d_model)
self.muti_atten = Mutihead_Attention(config.d_model,config.dim_k,config.dim_v,config.n_heads)
self.feed_forward = Feed_Forward(config.d_model)
self.add_norm = Add_Norm()
def forward(self,x):
x += self.positional_encoding(x.shape[1],config.d_model)
print("After positional_encoding:{}".format(x.size()))
output = self.add_norm(x,self.muti_atten,y=x)
output = self.add_norm(output,self.feed_forward)
return output
第一块导入包没啥好说的,正常导入就可以了
第二块就是定义encoder的类和模块了
首先是__init__初始化,具体就是图1的几个encoder的部分:
(1)这一行代码是在进行位置编码(positional encoding)。位置编码通常用于将序列中不同位置的元素进行编码,以便模型能够理解元素之间的顺序关系。在这里,x 是输入张量,self.positional_encoding 是一个位置编码的模块,它接受两个参数:序列长度和模型的维度。位置编码的结果会与输入张量 x 相加,以将位置信息加入到输入中。
(2)print("After positional_encoding:{}".format(x.size())):这一行代码打印了位置编码之后的张量 x 的大小。这可以用来调试和检查模型的输出大小。
(3)output = self.add_norm(x,self.muti_atten,y=x):这一行代码进行了多头注意力机制(multi-head attention)。多头注意力机制是一种神经网络中常用的注意力机制,用于处理序列数据。在这里,self.muti_atten 是一个多头注意力机制的模块,它接受输入张量 x 和一个可选的额外张量 y(通常是用于计算注意力权重的另一个输入)。self.add_norm 则是一个加法归一化的模块,用于对注意力机制的输出进行加法归一化处理。
(4)output = self.add_norm(output,self.feed_forward):这一行代码进行了前馈神经网络(feed-forward neural network)的处理。前馈神经网络通常用于对序列中的每个元素进行非线性变换。在这里,self.feed_forward 是一个前馈神经网络的模块,它接受多头注意力机制的输出 output,并对其进行进一步的非线性变换。然后,再次使用 self.add_norm 进行加法归一化处理,得到最终的输出 output。
1.0先讲一个函数:Add_Norm()
self.add_norm = Add_Norm()Add_Norm 可能是一种常见的神经网络中的操作,通常用于残差连接(Residual Connection)和层归一化(Layer Normalization)。
-
残差连接(Residual Connection):残差连接是一种在神经网络中常用的技术,用于解决深层网络训练过程中的梯度消失和梯度爆炸问题。在残差连接中,原始输入通过一个或多个层进行处理后,与输入相加,而不是覆盖掉原始输入。这种机制有助于传播梯度并简化模型的优化过程。
-
层归一化(Layer Normalization):层归一化是一种用于神经网络中的归一化技术,类似于批量归一化(Batch Normalization),但是它是对每个样本的特征进行归一化,而不是对整个批次进行归一化。层归一化可以帮助加速训练过程,提高模型的鲁棒性,并且通常用于深层网络中。
残差连接(Residual Connection)是一种在深度神经网络中常用的技术,用于解决深层网络训练过程中的梯度消失(vanishing gradients)和梯度爆炸(exploding gradients)等问题。

其中,𝐹(input)F(input) 表示经过神经网络层处理后的结果,inputinput 表示原始输入。通过将输出和输入进行相加,可以在不丢失信息的情况下,传递梯度,即使在网络变得非常深时也能保持梯度的稳定性。
残差连接的提出主要是由于深层神经网络中存在的退化问题。当网络变得非常深时,由于梯度消失等问题,网络的性能会下降,训练过程变得困难。通过残差连接,可以有效地解决这些问题,使得训练更加稳定,模型的性能也更好。
1.0.1这样的残差连接意义在哪里?误差不是会很大吗与全连接相比?
残差连接的主要意义在于解决深层神经网络中的梯度消失和模型退化问题,而不是误差的增加。
1.0.2这里的“残差”体现在什么地方?
残差体现在残差连接的设计中。在残差连接中,残差指的是原始输入和经过某些神经网络层处理后的输出之间的差异。
具体来说,残差连接的设计如下:
-
首先,将原始输入数据 𝑥x 输入到一个神经网络中的一个或多个层中,得到输出 𝐹(𝑥)F(x)。这里 𝐹F 表示这些层的组合。
-
然后,将原始输入 𝑥x 与输出 𝐹(𝑥)F(x) 相加,得到残差连接的结果。即:𝑥+𝐹(𝑥)x+F(x)。
-
最后,将残差连接的结果传递给网络的后续层进行进一步处理。
在这个过程中,残差 𝑥+𝐹(𝑥)x+F(x) 表示了原始输入 𝑥x 和经过网络处理后的输出 𝐹(𝑥)F(x) 之间的差异。这种设计允许模型学习到残差 𝐹(𝑥)F(x),而不是直接学习原始输入 𝑥x。这使得模型更容易学习到原始输入中的细微变化和重要特征,同时避免了梯度消失问题。
因此,残差体现在残差连接的设计中,它表示了网络在学习过程中需要添加的额外信息,以便更好地拟合数据并提高模型的性能。
1.0.3为什么梯度会消失?
梯度消失通常是在深度神经网络中训练过程中出现的问题。它指的是当梯度在反向传播过程中通过多个层传递时逐渐变小,最终变得非常接近于零,导致网络的参数几乎不再更新,从而无法有效地学习。
梯度消失的主要原因包括:
-
激活函数的选择:某些常用的激活函数(例如 Sigmoid 函数和 tanh 函数)在输入值较大或较小时会饱和,导致梯度接近于零。在深层网络中,多次使用这些激活函数会使得梯度逐渐消失。
-
权重初始化:不恰当的权重初始化可能导致梯度消失。例如,过大或过小的初始权重可能会导致激活函数在其饱和区域内,从而使得梯度消失。
-
深度网络结构:在深度网络中,梯度必须通过多个层传递,每一层都可能导致梯度衰减。当网络变得非常深时,梯度消失的问题会变得更加严重。
-
优化器的选择:某些优化算法可能无法有效地处理梯度消失的问题。例如,常用的随机梯度下降(SGD)算法可能在网络较深时表现不佳。
1.1先讲一下位置编码这块:
self.positional_encoding = Positional_Encoding(config.d_model) 位置编码是一种用于将序列中不同位置的信息编码成向量形式的技术,通常应用于处理序列数据的神经网络模型中,例如自然语言处理中的Transformer模型。表示序列顺序 位置信息的东西。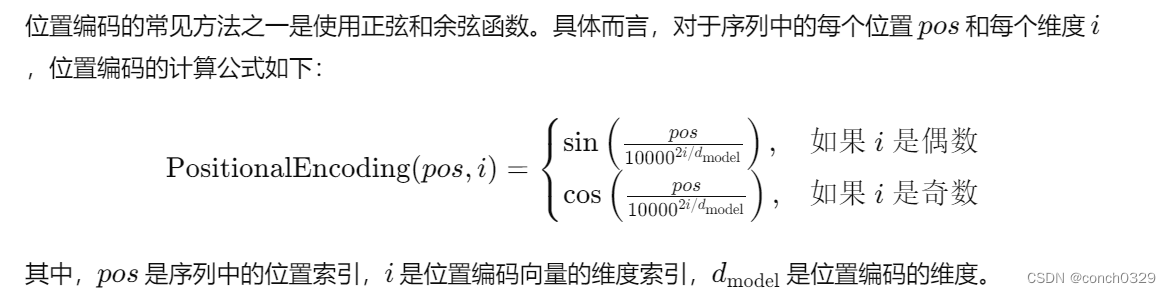



x += self.positional_encoding(x.shape[1],config.d_model)这行代码是将位置编码添加到输入张量 x 中。举个例子啊!
假设我们有一个输入张量 x,形状为 [2, 3, 4],表示一个批量大小为 2,序列长度为 3,每个单词的嵌入维度为 4 的输入序列。我们用以下张量来表示这个输入:
x = [[[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12]],
[[13, 14, 15, 16],
[17, 18, 19, 20],
[21, 22, 23, 24]]]
假设我们的位置编码维度是 4,因此每个位置编码向量的长度也是 4。我们的序列长度是 3,因此我们需要计算 3 个位置的位置编码。让我们假设位置编码的计算公式是将每个位置的索引除以 10 得到一个固定的位置编码向量。
根据上述假设,我们可以得到以下位置编码向量:
positional_encoding(3, 4) = [[0.0, 0.1, 0.2, 0.3],
[0.0, 0.1, 0.2, 0.3],
[0.0, 0.1, 0.2, 0.3]]
现在,我们将这个位置编码矩阵加到输入张量 x 中。由于 x 的第二个维度是序列长度,因此我们将位置编码矩阵添加到 x 的第二个维度上。即,对于每个批量和每个单词位置,我们将对应的位置编码向量加到 x 中。
最终,我们得到的输入张量 x 如下所示:
x = [[[1.0, 2.1, 3.2, 4.3],
[5.0, 6.1, 7.2, 8.3],
[9.0, 10.1, 11.2, 12.3]],
[[13.0, 14.1, 15.2, 16.3],
[17.0, 18.1, 19.2, 20.3],
[21.0, 22.1, 23.2, 24.3]]]
1.2然后是多头注意力机制
主要参考了这个视频链接注意力机制的本质|Self-Attention|Transformer|QKV矩阵_哔哩哔哩_bilibili
具体大家可以去看,我把主要公式写一下:
先举个例子: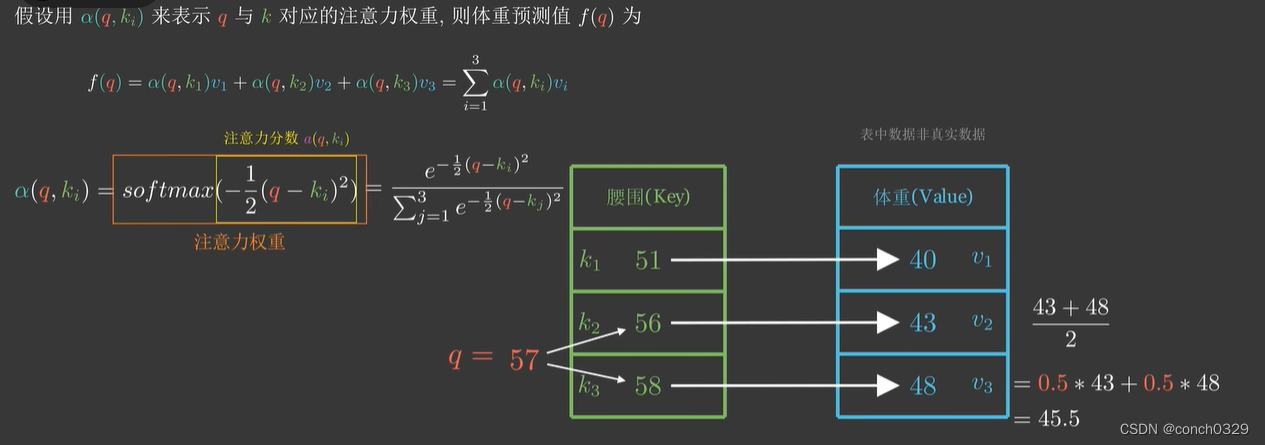
 qkv就是这么来的
qkv就是这么来的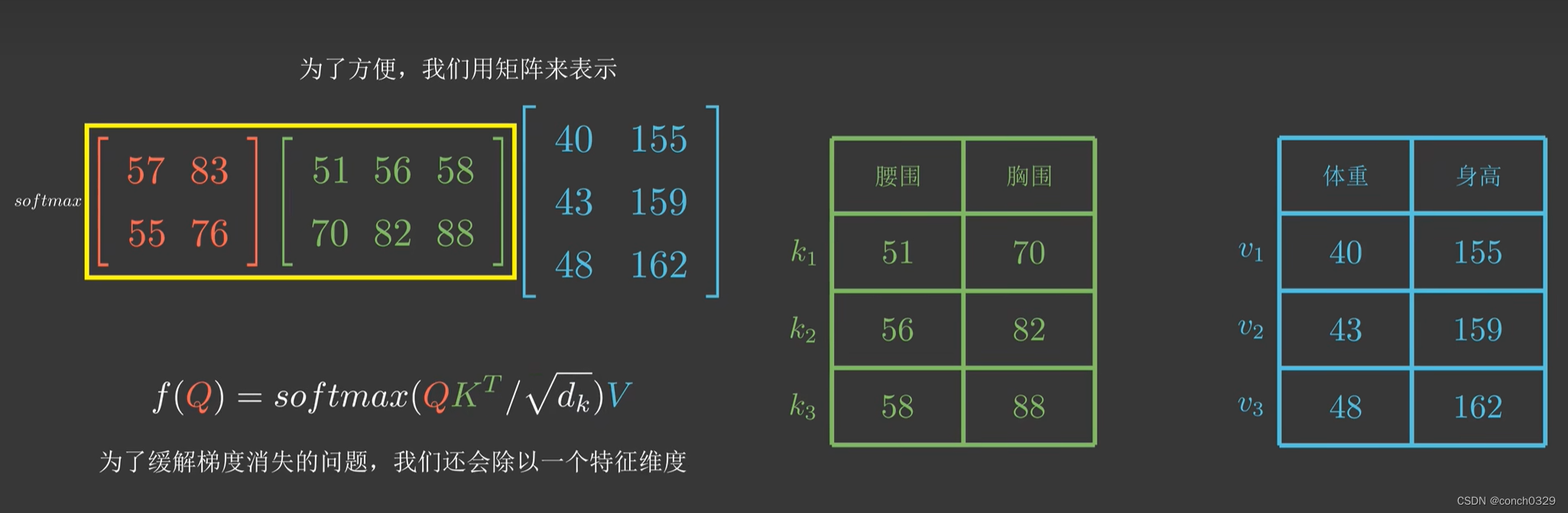
后面还有一个例子是自注意力机制。
1.2.1什么叫做一个头?
在多头注意力机制中,一个"头"指的是注意力机制中的一个独立计算单元。多头注意力机制通过同时使用多个这样的"头"来执行并行的注意力计算,以捕捉不同的注意力模式和信息。
每个注意力头都有自己的查询、键和数值映射,并独立计算注意力分数、注意力权重和加权和。通过使用多个注意力头,模型能够同时关注输入序列的不同部分,并学习到不同的特征表示。这有助于提高模型的表达能力和学习能力,使得模型能够更好地处理输入序列中的复杂关系。
#多头自注意力机制
class Mutihead_Attention(nn.Module):
def __init__(self,d_model,dim_k,dim_v,n_heads):
super(Mutihead_Attention,self).__init_()
self.dim_v = dim_v
self.dim_k = dim_k
self.n_heads = n_heads
self.q = nn.Linear(d_model,dim_k)
self.k = nn.Linear(d_model,dim_k)
self.dim_v = nn.Linear(d_model,dim_v)
self.o = nn.Linear(dim_v,d_model)
self.norm_fact = 1/math.sqrt(d_model)
def generate_mask(self,dim):
matirx = np.ones((dim,dim))
mask = torch.Tensor(np.tril(matirx))
return mask ==1
def forward(self,x,y,requires_mask=False):
assert self.dim_k % self.n_heads == 0 and self.dim_v % self.n_heads ==0
Q = self.q(x).reshape(-1,x.shape[0],x.shape[1],self.dim_k // self.n_heads)
K = self.k(x).reshape(-1,x.shape[0],x.shape[1],self.dim_k // self.n_heads)
V = self.k(x).reshape(-1,x.shape[0],x.shape[1],self.dim_k // self.n_heads)
# print("Attention V shape : {}".format(V.shape))
attention_score = torch.matmul(Q,K.permute(0,1,3,2)) * self.norm_fact
if requires_mask:
mask = self.generate_mask(x.shape[1])
attention_score.masked_fill(mask,value=float("-inf"))
output = torch.matul(attention_score,V).reshape(y.shape[0],y.shape[1],-1)1.3中间有涉及一些张量运算,参考这个视频链接
22.lesson12 基本运算_哔哩哔哩_bilibili
1.4我之前对残差连接理解的不到位,感觉还是原文作者分析的较好一些,
可以参考这个文章后面部分
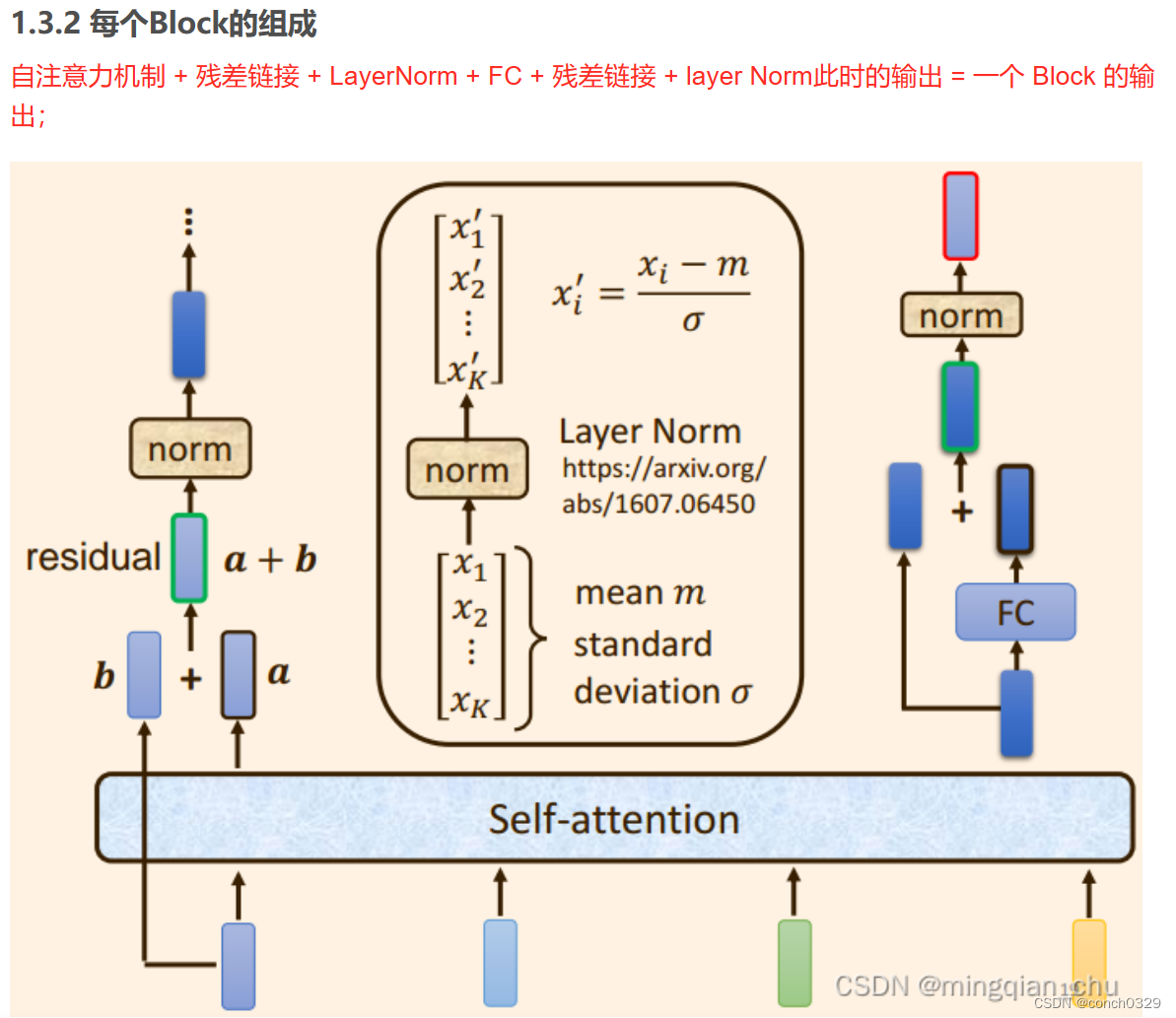
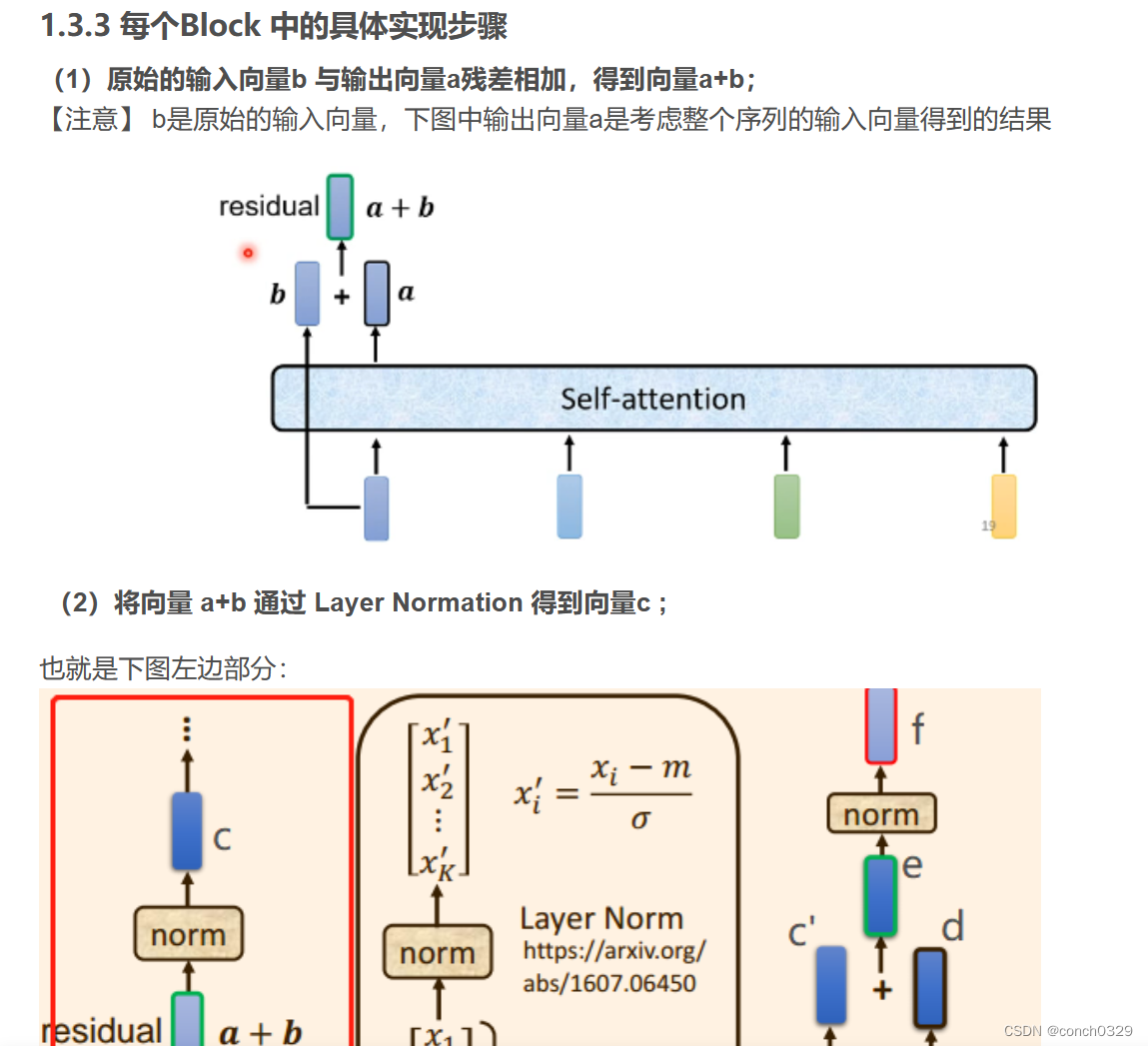
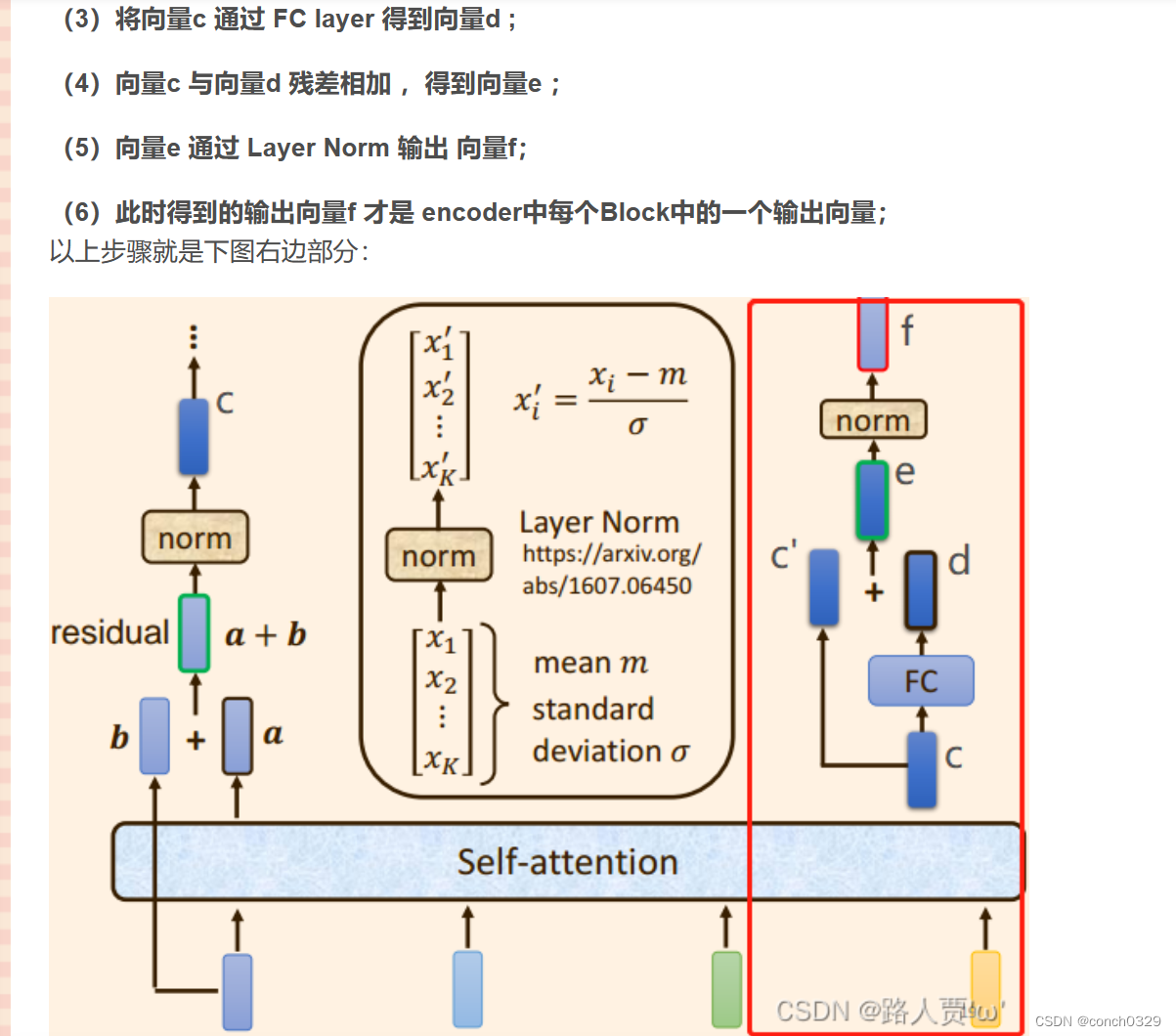
2.decoder部分
2.1self_attention 和maskattention的区别
self——attention
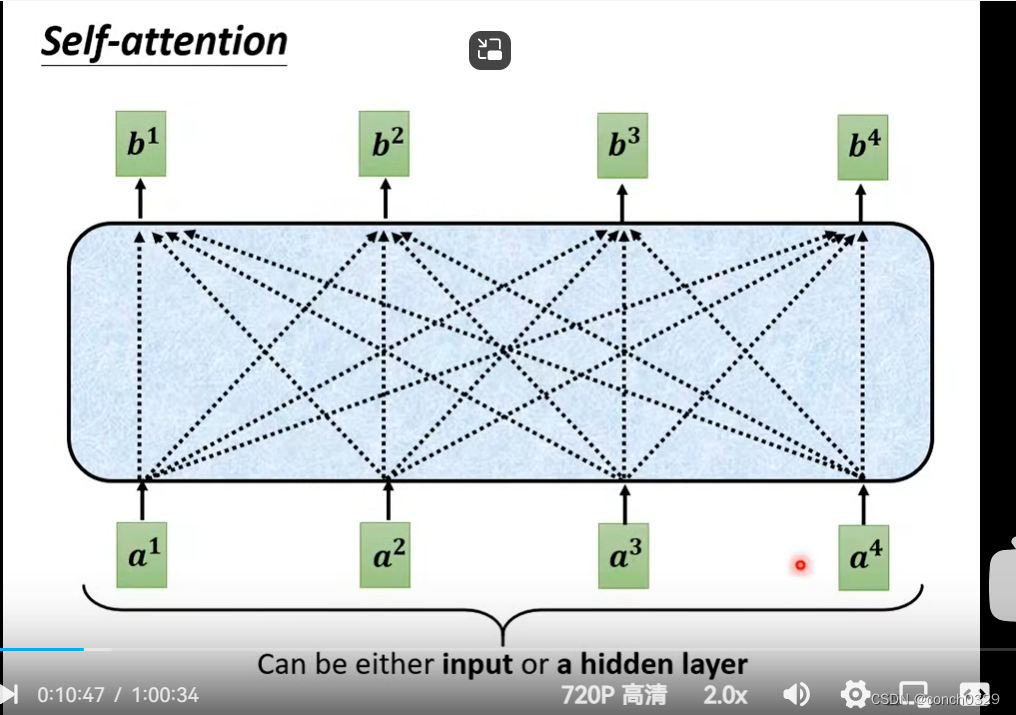 b1是由a1 a2 a3 a4共同决定的
b1是由a1 a2 a3 a4共同决定的
maskatten
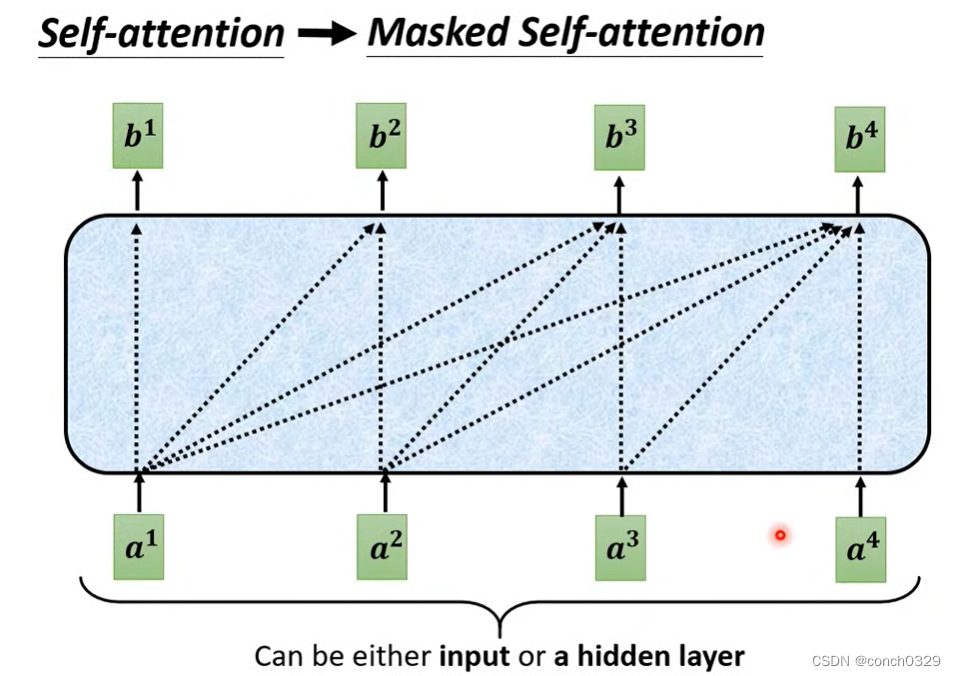 b1由a1决定,b2由a1 a2决定,b3由a1 a2 a3决定
b1由a1决定,b2由a1 a2决定,b3由a1 a2 a3决定
2.2encoder与decoder的区别与联系
2.3.5 具体实现步骤
(1)经过 Masked self attention:
解码器之前的输出作为当前解码器的输入,并且训练过程中真实标签的也会输入到解码器中,此时这些输入, 通过一个Masked self-attention ,得到输出q向量,注意到这里的q是由解码器产生的;(2)经过 Cross attention:
将向量q 与来自编码器的输出向量 k , v 运算。具体讲来就是向量 q 与向量 k之间相乘求出注意力分数α1 ',注意力分数α1 '再与向量 v 相乘求和,得出向量 b ;(3)经过全连接层:
之后向量 b 便被输入到feed−forward 层, 也即全连接层, 得到最终输出;
以上这段 我抄的