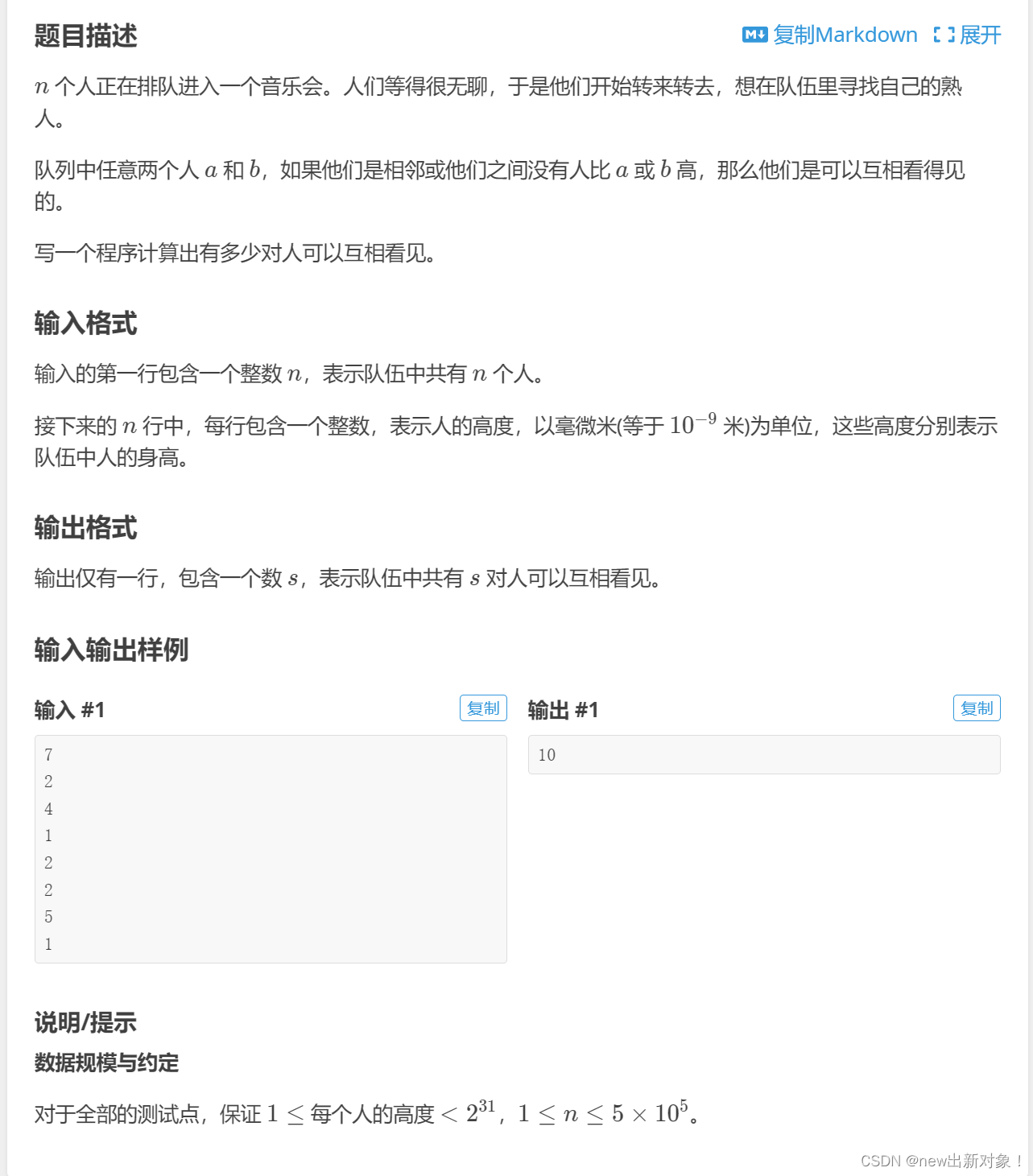
题目链接:https://leetcode.cn/problems/missing-number-lcci/description/
菜鸡做法:
#include <stdlib.h> // 包含标准库头文件,用于内存分配等功能
// 函数定义:寻找缺失的数字
int missingNumber(int* nums, int numsSize){
// 使用calloc分配内存并初始化为0,大小为numsSize+1,因为缺失的数字在0到numsSize之间
int *buffer = calloc(numsSize + 1, sizeof(int));
// 遍历数组,标记出现过的数字
for(int i = 0; i < numsSize; i++) {
buffer[nums[i]] = 1; // 将出现过的数字对应的位置标记为1
}
// 再次遍历buffer数组,寻找未被标记的位置
for(int i = 0; i < numsSize + 1; i++) {
if(buffer[i] == 0) { // 如果某位置为0,说明该数字未出现过
free(buffer); // 释放之前分配的内存
return i; // 返回缺失的数字
}
}
free(buffer); // 释放内存
return -1; // 如果所有数字都出现过,按题意这种情况不会发生,返回-1作为错误标志
}更好的做法:
数学:
我们知道,从0到n的整数之和可以用等差数列求和公式表示为 n * (n + 1) / 2。我们可以先计算出这个和,然后减去数组中所有数字的和,得到的结果就是缺失的数字。
下面是使用求和公式解决这个问题的代码实现,并加上了注释:
#include <stddef.h> // 包含标准库头文件,用于NULL等常量
// 函数定义:寻找缺失的数字
int missingNumber(int* nums, int numsSize) {
// 计算从0到numsSize的整数之和
int total = numsSize * (numsSize + 1) / 2;
// 计算数组中所有数字的和
int arraySum = 0;
for (int i = 0; i < numsSize; i++) {
arraySum += nums[i];
}
// 缺失的数字就是总和减去数组中数字的和
int missing = total - arraySum;
// 返回缺失的数字
return missing;
}
在这个实现中,没有使用额外的内存空间,因此也没有内存释放的操作。这种方法的时间复杂度是O(n),空间复杂度是O(1),是一种比较高效的解决方案。
利用异或的性质:
使用位运算解决寻找缺失数字的问题,可以利用异或运算的性质:一个数和它本身进行异或运算结果为0,一个数和0进行异或运算结果为它本身。因此,可以将数组中的所有数字和0到n(n为数组长度)的所有数字进行异或运算,最终的结果就是缺失的数字。
下面是使用位运算解决这个问题的代码实现:
#include <stddef.h> // 包含标准库头文件,用于NULL等常量
// 函数定义:寻找缺失的数字
int missingNumber(int* nums, int numsSize) {
int missing = numsSize; // 初始化缺失的数字为数组长度
for (int i = 0; i < numsSize; i++) {
missing ^= i ^ nums[i]; // 对数组中的数字和0到numsSize的数字进行异或运算
}
return missing; // 返回缺失的数字
}
在这个实现中,不需要分配额外的内存空间,因此也没有内存释放的操作。这种方法的时间复杂度是O(n),空间复杂度是O(1),比使用额外数组的方法更加高效。
这段代码实现了一个寻找数组中缺失数字的函数,它体现了以下哲学和编程思想:
-
对称性与互补性:在数学和哲学中,对称性和互补性是重要的概念。在这个算法中,通过异或运算(XOR)来寻找缺失的数字,利用了异或运算的对称性:任何数与自身异或结果为0,任何数与0异或结果为原数。这种对称性在算法中被用来消除成对的重复数字,从而揭示出缺失的数字。
-
简洁性:编程中的一个重要原则是KISS(Keep It Simple, Stupid),即保持代码的简洁性。这个算法通过一个简单的循环和异或运算就解决了问题,没有使用复杂的结构或额外的空间,体现了代码的简洁和高效。
-
数学思维:编程常常需要将问题抽象成数学模型来解决。在这个算法中,通过数学上的异或运算来处理数据,体现了数学思维在编程中的应用。
-
逻辑推理:算法的设计基于逻辑推理,即通过已知的数学性质(异或运算的性质)来推导出解决问题的方法。这种逻辑推理是编程解决问题的基础。
-
优化思想:在编程中,优化是一个重要的考虑因素。这个算法的时间复杂度是O(n),空间复杂度是O(1),是一种时间和空间上都高效的解决方案,体现了优化思想。
-
不变性:在函数式编程中,不变性是一个重要的概念,即数据一旦创建就不应该被修改。虽然这个算法不是函数式编程的例子,但它利用了异或运算的不变性来处理数据,即通过异或运算不会改变原始数据,而是产生新的结果。
-
抽象与封装:这个算法将寻找缺失数字的逻辑封装在一个函数中,对外部隐藏了实现细节,只提供了一个简单的接口。这种抽象和封装是良好软件设计的基础。
举一反三——异或能够解决哪些问题?:
位异或操作是一种非常有用的位操作,它可以解决多种编程和算法问题,特别是那些涉及成对出现的元素或需要在不使用额外空间的情况下操作数据的问题。以下是一些可以通过位异或操作解决的问题类型及示例:
找出唯一未成对的数字:
在一个数组中,每个元素都成对出现,只有一个元素是唯一的。使用异或可以找到这个唯一的元素,因为相同的数字异或结果为0,任何数字与0异或结果为其本身。
// 函数定义:寻找只出现一次的数字
int singleNumber(int* nums, int numsSize) {
int result = 0; // 初始化结果变量为0
for (int i = 0; i < numsSize; i++) {
result ^= nums[i]; // 对数组中的每个元素进行异或运算
}
return result; // 返回结果,即只出现一次的数字
}
交换两个变量:不使用临时变量交换两个变量的值。
// 函数定义:交换两个整数的值
void swap(int *x, int *y) {
if (*x != *y) { // 检查两个指针指向的值是否不同,避免相同的内存地址操作,导致结果归零
// 通过异或运算交换两个数的值
*x ^= *y; // 将x的值与y的值进行异或,结果保存回x
*y ^= *x; // 将y的值与上一步的结果(x的新值)进行异或,得到x的原始值,保存回y
*x ^= *y; // 将x的值与y的新值(x的原始值)进行异或,得到y的原始值,保存回x
}
}
例子说明过程:
假设我们有两个整数a = 5和b = 3,我们想要交换它们的值。我们可以通过调用swap(&a, &b)来实现。
- 初始状态:
a = 5,b = 3。 - 执行
*x ^= *y;:a = a ^ b = 5 ^ 3 = 6。 - 执行
*y ^= *x;:b = b ^ a = 3 ^ 6 = 5(此时b已经变成了a的原始值)。 - 执行
*x ^= *y;:a = a ^ b = 6 ^ 5 = 3(此时a已经变成了b的原始值)。
最终结果:a = 3,b = 5,成功交换了两个数的值。
注意:如果x和y指向的是同一个内存地址,即*x和*y是同一个数,那么上述交换操作会导致该数变为0,因为任何数与自身异或的结果都是0。因此,函数中加入了if (*x != *y)的检查来避免这种情况。
找出两个唯一未成对的数字:
在一个数组中,除了两个数字是唯一的,其他都成对出现。可以通过异或分组的方式找到这两个唯一的数字。
void findTwoUniqueNumbers(int* nums, int numsSize, int* num1, int* num2) {
int xor = 0;
// 第一次遍历:对数组中所有元素执行异或操作。
// 相同的数字会相互抵消,最终结果是两个唯一数字的异或结果。
for (int i = 0; i < numsSize; i++) {
xor ^= nums[i];
}
// 找到异或结果中任意一个为1的位,我们这里选择最右边的一个。
// 这一位能够帮助我们区分两个唯一的数字。
int rightmostSetBit = xor & ~(xor - 1);
*num1 = 0; // 初始化结果变量
*num2 = 0; // 初始化结果变量
// 第二次遍历:根据rightmostSetBit将数组分组,并分别异或。
// 因为rightmostSetBit是两个唯一数字之间的不同位,所以它可以将这两个数字
// 分到不同的组中,而成对出现的数字会被分到同一组并在异或中抵消。
for (int i = 0; i < numsSize; i++) {
if ((nums[i] & rightmostSetBit) != 0) {
// 如果nums[i]在rightmostSetBit位上是1,说明它和其中一个唯一数字
// 在该位上不同,因此将其与num1进行异或运算。
*num1 ^= nums[i];
} else {
// 否则,说明它和另一个唯一数字在该位上不同,将其与num2进行异或运算。
*num2 ^= nums[i];
}
}
}数组中的两个元素求和:
虽然异或操作本身不直接用于求和,但在某些特定的位操作问题中,如求两个非负整数的和而不使用加号或其他算术运算符时,可以用异或来模拟加法操作中的“不进位求和”,同时用与操作和左移操作来模拟进位操作。