深度学习中的注意力机制二（Pytorch 16）

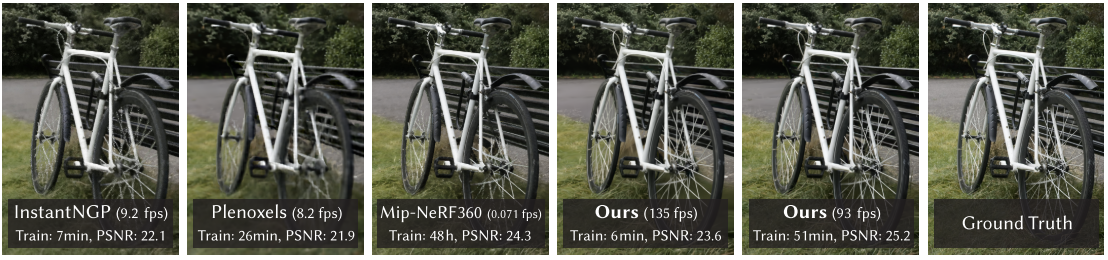
一 Bahdanau 注意力

通过设计一个 基于两个循环神经网络的编码器‐解码器架构，用于序列到序列学习。具体来说，循环神经网络编码器将长度可变的序列转换为固定形状的上下文变量，然后循环神经网络解码器根据生成的词元和上下文变量按词元生成输出（目标）序列词元。然而，即使并非所有输入（源）词元都对解码某个词元都有用，在每个解码步骤中仍使用编码相同的上下文变量。有什么方法能改变上下文变量呢？

我们试着从 (Graves, 2013)中找到灵感：在为给定文本序列生成手写的挑战中，Graves设计了一种可微注意力模型，将文本字符与更长的笔迹对齐，其中对齐方式仅向一个方向移动。受学习对齐想法的启发，Bahdanau等人提出了一个没有严格单向对齐限制的可微注意力模型 (Bahdanau et al., 2014)。在预测词元时，如果不是所有输入词元都相关，模型将仅对齐（或参与）输入序列中与当前预测相关的部分。这是通过将上下文变量视为注意力集中的输出来实现的。

1.1 定义模型

下面描述的Bahdanau注意力模型将遵循上节中的相同符号表达。这个新的基于注意力的模型与上节节中的模型相同，只不过之前中的上下文变量c 在任何解码时间步t ′都会被ct ′替换。假设输入序列中有T个词元，解码时间步t ′的上下文变量是注意力集中的输出：

import torch
from torch import nn
from d2l import torch as d2l

#@save
class AttentionDecoder(d2l.Decoder):
    """带有注意力机制解码器的基本接口"""
    def __init__(self, **kwargs):
        super(AttentionDecoder, self).__init__(**kwargs)
        
    @property
    def attention_weights(self):
        raise NotImplementedError

接下来，让我们在接下来的Seq2SeqAttentionDecoder类中实现带有Bahdanau注意力的循环神经网络解码器。首先，初始化解码器的状态，需要下面的输入：

编码器在所有时间步的最终层隐状态，将作为注意力的键和值；
上一时间步的 编码器全层隐状态，将作为初始化解码器的隐状态；
编码器有效长度（排除在注意力池中填充词元）。在每个解码时间步骤中，解码器上一个时间步的最终层隐状态将用作查询。因此，注意力输出和输入嵌入都 连结为循环神经网络解码器的输入。

class Seq2SeqAttentionDecoder(AttentionDecoder):
    def __init__(self, vocab_size, embed_size, num_hiddens, num_layers,
                 dropout=0, **kwargs):
        super(Seq2SeqAttentionDecoder, self).__init__(**kwargs)
        self.attention = d2l.AdditiveAttention(
            num_hiddens, num_hiddens, num_hiddens, dropout)
        self.embedding = nn.Embedding(vocab_size, embed_size)
        self.rnn = nn.GRU(
            embed_size + num_hiddens, num_hiddens, num_layers,
            dropout=dropout)
        self.dense = nn.Linear(num_hiddens, vocab_size)
    
    def init_state(self, enc_outputs, enc_valid_lens, *args):
        # outputs的形状为(batch_size，num_steps，num_hiddens).
        # hidden_state的形状为(num_layers，batch_size，num_hiddens)
        outputs, hidden_state = enc_outputs
        return (outputs.permute(1, 0, 2), hidden_state, enc_valid_lens)

    def forward(self, X, state):
        # enc_outputs的形状为(batch_size,num_steps,num_hiddens).
        # hidden_state的形状为(num_layers,batch_size,
        # num_hiddens)
        enc_outputs, hidden_state, enc_valid_lens = state
        # 输出X的形状为(num_steps,batch_size,embed_size)
        X = self.embedding(X).permute(1, 0, 2)
        outputs, self._attention_weights = [], []
        for x in X:
            # query的形状为(batch_size,1,num_hiddens)
            query = torch.unsqueeze(hidden_state[-1], dim=1)
            # context的形状为(batch_size,1,num_hiddens)
            context = self.attention(
                query, enc_outputs, enc_outputs, enc_valid_lens)
            # 在特征维度上连结
            x = torch.cat((context, torch.unsqueeze(x, dim=1)), dim=-1)
            # 将x变形为(1,batch_size,embed_size+num_hiddens)
            out, hidden_state = self.rnn(x.permute(1, 0, 2), hidden_state)
            outputs.append(out)
            self._attention_weights.append(self.attention.attention_weights)
        # 全连接层变换后，outputs的形状为
        # (num_steps,batch_size,vocab_size)
        outputs = self.dense(torch.cat(outputs, dim=0))
        return outputs.permute(1, 0, 2), [enc_outputs, hidden_state,
                                          enc_valid_lens]
    @property
    def attention_weights(self):
        return self._attention_weights

接下来，使用包含7个时间步的4个序列输入的 小批量测试Bahdanau注意力解码器。

encoder = d2l.Seq2SeqEncoder(vocab_size=10, embed_size=8, num_hiddens=16,
                             num_layers=2)
encoder.eval()
decoder = Seq2SeqAttentionDecoder(vocab_size=10, embed_size=8, num_hiddens=16,
                                  num_layers=2)
decoder.eval()
X = torch.zeros((4, 7), dtype=torch.long) # (batch_size,num_steps)
state = decoder.init_state(encoder(X), None)
output, state = decoder(X, state)
output.shape, len(state), state[0].shape, len(state[1]), state[1][0].shape
# (torch.Size([4, 7, 10]), 3, torch.Size([4, 7, 16]), 2, torch.Size([4, 16]))

1.2 执行训练

我们在这里指定超参数，实例化一个带有Bahdanau注意力的编码器和解码器，并对这个模型进行机器翻译训练。由于 新增的注意力机制，训练要比没有注意力机制的 9.7.4节慢得多。

embed_size, num_hiddens, num_layers, dropout = 32, 32, 2, 0.1
batch_size, num_steps = 64, 10
lr, num_epochs, device = 0.005, 250, d2l.try_gpu()

train_iter, src_vocab, tgt_vocab = d2l.load_data_nmt(batch_size, num_steps)
encoder = d2l.Seq2SeqEncoder(
    len(src_vocab), embed_size, num_hiddens, num_layers, dropout)
decoder = Seq2SeqAttentionDecoder(
    len(tgt_vocab), embed_size, num_hiddens, num_layers, dropout)
net = d2l.EncoderDecoder(encoder, decoder)
d2l.train_seq2seq(net, train_iter, lr, num_epochs, tgt_vocab, device)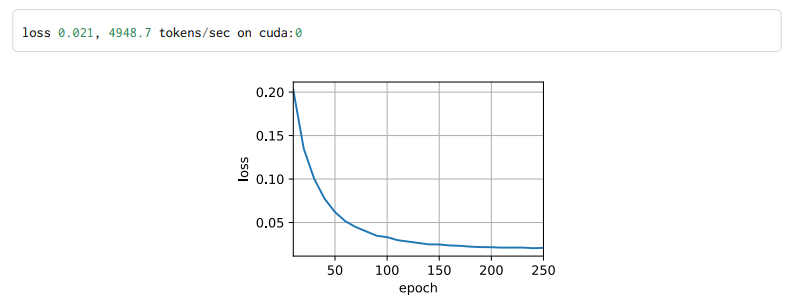

模型训练后，我们用它将几个英语句子 翻译成法语并计算它们的BLEU分数。

engs = ['go .', "i lost .", 'he\'s calm .', 'i\'m home .']
fras = ['va !', 'j\'ai perdu .', 'il est calme .', 'je suis chez moi .']
for eng, fra in zip(engs, fras):
    translation, dec_attention_weight_seq = d2l.predict_seq2seq(
        net, eng, src_vocab, tgt_vocab, num_steps, device, True)
    print(f'{eng} => {translation}, ',
          f'bleu {d2l.bleu(translation, fra, k=2):.3f}')

# go . => va !, bleu 1.000
# i lost . => j'ai perdu ., bleu 1.000
# he's calm . => il est paresseux ., bleu 0.658
# i'm home . => je suis chez moi ., bleu 1.000

训练结束后，下面通过可视化注意力权重会发现，每个查询都会在键值对上分配不同的权重，这说明在每个解码步中，输入序列的不同部分被选择性地聚集在注意力池中。

# 加上一个包含序列结束词元
d2l.show_heatmaps(
    attention_weights[:, :, :, :len(engs[-1].split()) + 1].cpu(),
    xlabel='Key positions', ylabel='Query positions')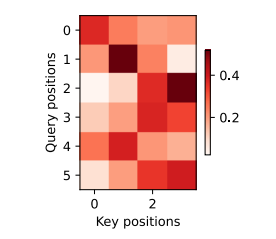

小结：

在预测词元时，如果不是所有输入词元都是相关的，那么具有Bahdanau注意力的循环神经网络编码器‐解码器会有选择地统计输入序列的不同部分。这是 通过将上下文变量视为加性注意力池化的输出来实现的。
在循环神经网络编码器‐解码器中，Bahdanau注意力将上一时间步的解码器隐状态视为查询，在所有时间步的编码器隐状态同时视为键和值。

二多头注意力

在实践中，当给定相同的查询、键和值的集合时，我们希望模型可以基于相同的注意力机制学习到不同的行为，然后将不同的行为作为知识组合起来，捕获序列内各种范围的依赖关系（例如，短距离依赖和长距离依赖关系）。因此，允许注意力机制组合使用查询、键和值的不同子空间表示（representation subspaces）可能是有益的。

为此，与其只使用单独一个注意力汇聚，我们可以 用独立学习得到的h组不同的线性投影（linear projections）来变换查询、键和值。然后，这h组变换后的查询、键和值将并行地送到注意力汇聚中。最后，将这h个注意力汇聚的输出拼接在一起，并且通过另一个可以学习的线性投影进行变换，以产生最终输出。这种设计被称为 多头注意力（multihead attention）(Vaswani et al., 2017)。对于h个注意力汇聚输出，每一个注意力汇聚都被称作一个头（head）。下图展示了使用全连接层来实现可学习的线性变换的多头注意力。

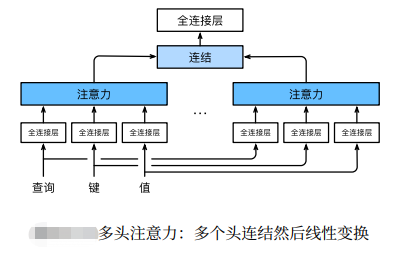
2.1 执行建模

基于这种设计，每个头都可能会关注输入的不同部分，可以表示比简单加权平均值更复杂的函数。

在实现过程中通常 选择缩放点积注意力作为每一个注意力头。为了避免计算代价和参数代价的大幅增长，我们设定pq = pk = pv = po/h。值得注意的是，如果将查询、键和值的线性变换的输出数量设置为 pqh = pkh = pvh = po，则可以并行计算h个头。在下面的实现中，po是通过参数num_hiddens指定的。

import math
import torch
from torch import nn
from d2l import torch as d2l

#@save
class MultiHeadAttention(nn.Module):
    """多头注意力"""
    def __init__(self, key_size, query_size, value_size, num_hiddens,
                 num_heads, dropout, bias=False, **kwargs):
        super(MultiHeadAttention, self).__init__(**kwargs)
        self.num_heads = num_heads
        self.attention = d2l.DotProductAttention(dropout)
        self.W_q = nn.Linear(query_size, num_hiddens, bias=bias)
        self.W_k = nn.Linear(key_size, num_hiddens, bias=bias)
        self.W_v = nn.Linear(value_size, num_hiddens, bias=bias)
        self.W_o = nn.Linear(num_hiddens, num_hiddens, bias=bias)
    
    def forward(self, queries, keys, values, valid_lens):
        # queries，keys，values的形状:
        # (batch_size，查询或者“键－值”对的个数，num_hiddens)
        # valid_lens　的形状:
        # (batch_size，)或(batch_size，查询的个数)
        # 经过变换后，输出的queries，keys，values　的形状:
        # (batch_size*num_heads，查询或者“键－值”对的个数，
        # num_hiddens/num_heads)
        queries = transpose_qkv(self.W_q(queries), self.num_heads)
        keys = transpose_qkv(self.W_k(keys), self.num_heads)
        values = transpose_qkv(self.W_v(values), self.num_heads)

        if valid_lens is not None:
            # 在轴0，将第一项（标量或者矢量）复制num_heads次，
            # 然后如此复制第二项，然后诸如此类。
            valid_lens = torch.repeat_interleave(
                valid_lens, repeats=self.num_heads, dim=0)
        # output的形状:(batch_size*num_heads，查询的个数，
        # num_hiddens/num_heads)
        output = self.attention(queries, keys, values, valid_lens)
        # output_concat的形状:(batch_size，查询的个数，num_hiddens)
        output_concat = transpose_output(output, self.num_heads)
        return self.W_o(output_concat)

为了能够使多个头并行计算，上面的MultiHeadAttention类将使用下面定义的 两个转置函数。具体来说，transpose_output函数反转了transpose_qkv函数的操作。

#@save
def transpose_qkv(X, num_heads):
    """为了多注意力头的并行计算而变换形状"""
    # 输入X的形状:(batch_size，查询或者“键－值”对的个数，num_hiddens)
    # 输出X的形状:(batch_size，查询或者“键－值”对的个数，num_heads，
    # num_hiddens/num_heads)
    X = X.reshape(X.shape[0], X.shape[1], num_heads, -1)
    # 输出X的形状:(batch_size，num_heads，查询或者“键－值”对的个数,
    # num_hiddens/num_heads)
    X = X.permute(0, 2, 1, 3)
    # 最终输出的形状:(batch_size*num_heads,查询或者“键－值”对的个数,
    # num_hiddens/num_heads)
    return X.reshape(-1, X.shape[2], X.shape[3])

#@save
def transpose_output(X, num_heads):
    """逆转transpose_qkv函数的操作"""
    X = X.reshape(-1, num_heads, X.shape[1], X.shape[2])
    X = X.permute(0, 2, 1, 3)
    return X.reshape(X.shape[0], X.shape[1], -1)

下面使用键和值相同的小例子来测试我们编写的MultiHeadAttention类。多头注意力输出的形状是（batch_size，num_queries，num_hiddens）。

num_hiddens, num_heads = 100, 5
attention = MultiHeadAttention(num_hiddens, num_hiddens, num_hiddens,
                               num_hiddens, num_heads, 0.5)
attention.eval()

# MultiHeadAttention(
#   (attention): DotProductAttention(
#     (dropout): Dropout(p=0.5, inplace=False)
#   )
#   (W_q): Linear(in_features=100, out_features=100, bias=False)
#   (W_k): Linear(in_features=100, out_features=100, bias=False)
#   (W_v): Linear(in_features=100, out_features=100, bias=False)
#   (W_o): Linear(in_features=100, out_features=100, bias=False)
# )

batch_size, num_queries = 2, 4
num_kvpairs, valid_lens = 6, torch.tensor([3, 2])
X = torch.ones((batch_size, num_queries, num_hiddens))
Y = torch.ones((batch_size, num_kvpairs, num_hiddens))
attention(X, Y, Y, valid_lens).shape  # torch.Size([2, 4, 100])

小结：

多头注意力融合了来自于多个注意力汇聚的不同知识，这些知识的不同来源于相同的查询、键和值的不同的子空间表示。
基于 适当的张量操作，可以 实现多头注意力 的 并行计算。

三自注意力和位置编码

在深度学习中，经常使用 卷积神经网络（CNN）或 循环神经网络（RNN）对序列进行编码。想象一下，有了注意力机制之后，我们 将词元序列输入注意力池化中，以便同一组词元同时充当查询、键和值。具体来说，每个查询都会关注所有的键－值对并生成一个注意力输出。由于查询、键和值来自同一组输入，因此被称为 自注意力（self‐attention）(Lin et al., 2017, Vaswani et al., 2017)，也被称为 内部注意力（intra‐attention）(Cheng et al., 2016, Parikh et al., 2016, Paulus et al., 2017)。本节将 使用自注意力进行序列编码，以及如何 使用序列的顺序 作为 补充信息。

3.1 自注意力

根据之前定义的注意力汇聚函数f。下面的代码片段是 基于多头注意力对一个张量完成自注意力的计算，张量的形状为（批量大小，时间步的数目或词元序列的长度，d）。输出与输入的张量形状相同。

import math
import torch
from torch import nn
from d2l import torch as d2l

num_hiddens, num_heads = 100, 5
attention = d2l.MultiHeadAttention(num_hiddens, num_hiddens, num_hiddens,
                                   num_hiddens, num_heads, 0.5)
attention.eval()

# MultiHeadAttention(
#   (attention): DotProductAttention(
#     (dropout): Dropout(p=0.5, inplace=False)
#   )
#   (W_q): Linear(in_features=100, out_features=100, bias=False)
#   (W_k): Linear(in_features=100, out_features=100, bias=False)
#   (W_v): Linear(in_features=100, out_features=100, bias=False)
#   (W_o): Linear(in_features=100, out_features=100, bias=False)
# )

batch_size, num_queries, valid_lens = 2, 4, torch.tensor([3, 2])
X = torch.ones((batch_size, num_queries, num_hiddens))
attention(X, X, X, valid_lens).shape
# torch.Size([2, 4, 100])

3.2 比较卷积神经网络、循环神经网络和自注意力

接下来比较下面几个架构，目标都是 将由n个词元组成的序列映射到另一个长度相等的序列，其中的每个输入词元或输出词元都由d维向量表示。具体来说，将比较的是 卷积神经网络、循环神经网络 和 自注意力 这几个架构的 计算复杂性、顺序操作和最大路径长度。请注意，顺序操作会妨碍并行计算，而任意的序列位置组合之间的路径越短，则能 更轻松地学习序列中的远距离依赖关系 (Hochreiter et al., 2001)。

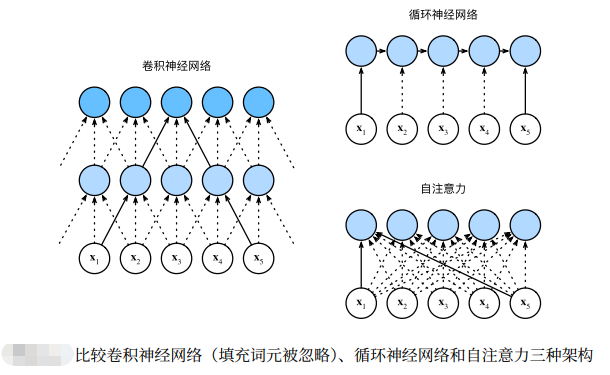
考虑一个 卷积核大小为k的卷积层。在后面的章节将提供关于使用卷积神经网络处理序列的更多详细信息。目前只需要知道的是，由于序列长度是n，输入和输出的通道数量都是d，所以 卷积层的计算复杂度为O(knd^2 )。如上图所示，卷积神经网络是分层的，因此为有O(1)个顺序操作，最大路径长度为O(n/k)。例如，x1和x5处于上图中 卷积核大小为3的双层卷积神经网络的感受野内。

当 更新循环神经网络的隐状态 时，d × d权重矩阵和d维隐状态的乘法计算复杂度为O(d^2 )。由于序列长度为n，因此 循环神经网络层的计算复杂度为O(nd^2 )。根据图10.6.1，有O(n)个顺序操作无法并行化，最大路径长度也是O(n)。

在 自注意力 中，查询、键和值都是n × d矩阵。缩放的”点－积“注意力，其中n × d矩阵乘以d×n矩阵。之后输出的n×n矩阵乘以n×d矩阵。因此，自注意力具有O(n^2d)计算复杂性。正如在上图中所讲，每个词元都通过自注意力直接连接到任何其他词元。因此，有O(1)个顺序操作可以并行计算，最大路径长度也是O(1)。

总而言之，卷积神经网络和自注意力都拥有并行计算的优势，而且 自注意力的最大路径长度最短。但是因为 其计算复杂度是关于序列长度的二次方，所以在很长的序列中计算会非常慢。

3.3 位置编码

在处理词元序列时，循环神经网络是逐个的重复地处理词元的，而 自注意力则因为并行计算而放弃了顺序操作。为了使用序列的顺序信息，通过在输入表示中添加 位置编码（positional encoding）来注入绝对的或相对的位置信息。位置编码可以通过学习得到也可以直接固定得到。接下来描述的是基于正弦函数和余弦函数的固定位置编码 (Vaswani et al., 2017)。

假设输入表示X ∈ R n×d 包含一个序列中n个词元的d维嵌入表示。位置编码使用相同形状的位置嵌入矩阵 P ∈ R n×d输出X + P，矩阵第i行、第2j列和2j + 1列上的元素为：

乍一看，这种基于三角函数的设计看起来很奇怪。在解释这个设计之前，让我们先在下面的PositionalEncoding类中实现它。

#@save
class PositionalEncoding(nn.Module):
    """位置编码"""
    def __init__(self, num_hiddens, dropout, max_len=1000):
        super(PositionalEncoding, self).__init__()
        self.dropout = nn.Dropout(dropout)
        # 创建一个足够长的P
        self.P = torch.zeros((1, max_len, num_hiddens))
        X = torch.arange(max_len, dtype=torch.float32).reshape(
            -1, 1) / torch.pow(10000, torch.arange(
            0, num_hiddens, 2, dtype=torch.float32) / num_hiddens)
        self.P[:, :, 0::2] = torch.sin(X)
        self.P[:, :, 1::2] = torch.cos(X)

    def forward(self, X):
        X = X + self.P[:, :X.shape[1], :].to(X.device)
        return self.dropout(X)

在位置嵌入矩阵P中，行代表词元在序列中的位置，列代表位置编码的不同维度。从下面的例子中可以看到位置嵌入矩阵的第6列和第7列的频率高于第8列和第9列。第6列和第7列之间的偏移量（第8列和第9列相同）是 由于正弦函数和余弦函数的交替。

encoding_dim, num_steps = 32, 60
pos_encoding = PositionalEncoding(encoding_dim, 0)
pos_encoding.eval()
X = pos_encoding(torch.zeros((1, num_steps, encoding_dim)))
P = pos_encoding.P[:, :X.shape[1], :]
d2l.plot(torch.arange(num_steps), P[0, :, 6:10].T, xlabel='Row (position)',
         figsize=(6, 2.5), legend=["Col %d" % d for d in torch.arange(6, 10)])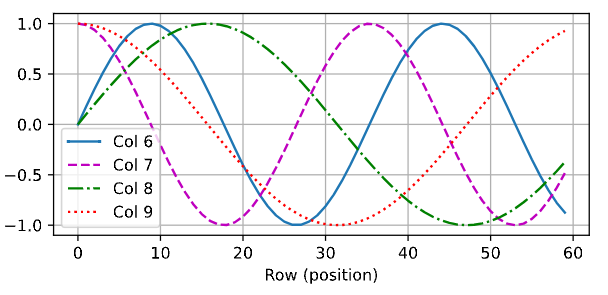

绝对位置信息，为了明白沿着编码维度单调降低的频率与绝对位置信息的关系，让我们打印出0, 1, . . . , 7的二进制表示形式。正如所看到的，每个数字、每两个数字和每四个数字上的比特值在第一个最低位、第二个最低位和第三个最低位上分别交替。

for i in range(8):
    print(f'{i}的二进制是：{i:>03b}')
    
# 0的二进制是：000
# 1的二进制是：001
# 2的二进制是：010
# 3的二进制是：011
# 4的二进制是：100
# 5的二进制是：101
# 6的二进制是：110
# 7的二进制是：111

在二进制表示中，较高比特位的交替频率低于较低比特位，与下面的热图所示相似，只是位置编码通过使用三角函数在编码维度上降低频率。由于输出是浮点数，因此此类连续表示比二进制表示法更节省空间。

P = P[0, :, :].unsqueeze(0).unsqueeze(0)
d2l.show_heatmaps(P, xlabel='Column (encoding dimension)',
                  ylabel='Row (position)', figsize=(3.5, 4), cmap='Blues')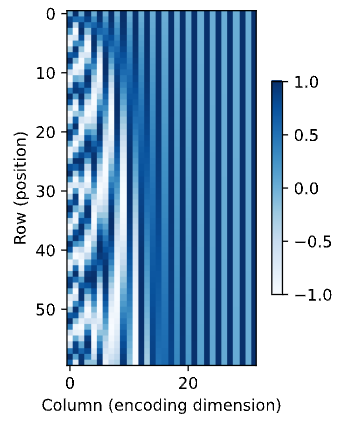

小结：

在 自注意力 中，查询、键和值都来自同一组输入。
卷积神经网络和自注意力都拥有并行计算的优势，而且 自注意力的最大路径长度最短。但是因为其计算复杂度是关于序列长度的二次方，所以在很长的序列中计算会非常慢。
为了 使用序列的顺序信息，可以通过 在输入表示中添加位置编码，来注入绝对的或相对的位置信息。